兩種群相互競(jìng)爭(zhēng)的具有脈沖接種的SEIR傳染病模型
周 文,侯高梅
(安徽師范大學(xué) 數(shù)學(xué)計(jì)算機(jī)科學(xué)學(xué)院,安徽 蕪湖 241000)
兩種群相互競(jìng)爭(zhēng)的具有脈沖接種的SEIR傳染病模型
周 文,侯高梅
(安徽師范大學(xué) 數(shù)學(xué)計(jì)算機(jī)科學(xué)學(xué)院,安徽 蕪湖 241000)
研究了一類兩種群相互競(jìng)爭(zhēng)的具有脈沖接種的SEIR傳染病模型,討論了系統(tǒng)周期解的存在性,并利用Floquet定理證明,在滿足一定條件下,周期解是局部漸近穩(wěn)定的。
競(jìng)爭(zhēng)系統(tǒng);脈沖接種;周期解;穩(wěn)定性
Kermark和Mekendrick在1927年首次建立了傳染病模型,此后越來(lái)越多的學(xué)者開(kāi)始研究傳染病模型[1-4]。在現(xiàn)實(shí)世界中,種群大多數(shù)都是相伴存在的。于是,在傳染病的研究中考慮在兩個(gè)或者多個(gè)種群的系統(tǒng)就比較重要,研究起來(lái)也就比較復(fù)雜[5-9]。本文主要在兩種群相互競(jìng)爭(zhēng)的系統(tǒng)中,結(jié)合脈沖接種對(duì)傳染病模型進(jìn)行研究,建立數(shù)學(xué)模型,討論模型周期解的存在性和穩(wěn)定性。
1 模型建立
考慮具有脈沖接種的兩種群相互競(jìng)爭(zhēng)的傳染病模型,具體如下:
系統(tǒng)(1)當(dāng)t≠k時(shí),
E1′(t)=S1(β11I1+β12I2)-[d1+(1-a1)·
mN2I1-γ1I1,
mN2R1-ρ1R1,
E2′(t)=S2(β21I1+β22I2)-[d2+(1-a2)·
nN1I2-γ2I2,
nN1R2-ρ2R2。
系統(tǒng)(2)當(dāng)t=k時(shí),
N1(t+)=N1(t),
S1(t+)=(1-θ1)S1(t),
E1(t+)=E1(t),
I1(t+)=I1(t),
R1(t+)=R1(t)+θ1S1(t),
N2(t+)=N2(t),
S2(t+)=(1-θ2)S2(t),
E2(t+)=E2(t),
I2(t+)=I2(t),
R2(t+)=R2(t)+θ2S2(t)。
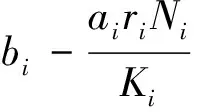
為了計(jì)算方便,由Ri=Ni-Si-Ei-Ii將系統(tǒng)(1)和(2)簡(jiǎn)化,當(dāng)t≠k時(shí),記為系統(tǒng)(3):
S1-E1-I1),
E1′(t)=S1(β11I1+β12I2)-[d1+(1-a1)·
mN2I1-γ1I1,
S2-E2-I2),
E2′(t)=S2(β21I1+β22I2)-[d2+(1-a2)·
nN1I2-γ2I2。
當(dāng)t=k時(shí),記為系統(tǒng)(4):
N1(t+)=N1(t),
S1(t+)=(1-θ1)S1(t),
E1(t+)=E1(t),
I1(t+)=I1(t),
N2(t+)=N2(t),
S2(t+)=(1-θ2)S2(t),
E2(t+)=E2(t),
I2(t+)=I2(t)。
考慮到生物學(xué)意義,系統(tǒng)(3)和(4)的可行域?yàn)?/p>
0≤Si+Ei+Ii≤Ni≤Ki,i=1,2}是系統(tǒng)(3)和(4)的正向不變集。
2 周期解的存在性
首先,周期解P0=(0,0,0,0,0,0,0,0)T是顯然存在的。
下面來(lái)討論周期解P1=(0,0,0,0,K2,0,0,0)T的存在性。此時(shí)等價(jià)于考慮如下系統(tǒng):
(5)
下面考慮周期解P2=(0,0,0,0,K2,S2,0,0)T的存在性。此時(shí)等價(jià)于考慮如下系統(tǒng):
(6)
記B=(b2-a2r2+ρ2)K2,A=d2+(1-a2)r2+ρ2,可解得
又S2(1)=(1-θ2)S2(0),則
B>0,則1-e-A>0。所以,當(dāng)1-θ2-e-A>0時(shí),有S2(0)>0,即周期解P2是存在的。
接下來(lái),考慮周期解P3=(0,0,0,0,K2,S2,E2,0)T的存在性。此時(shí)等價(jià)于考慮如下系統(tǒng):
(7)
同樣可解得:
E2(t)=e-(d2+(1-a2)r2+δ2+S2β22)t[E2(0)-
最后,考慮周期解P4=(0,0,0,0,K2,S2,E2,I2)T的存在性。此時(shí)等價(jià)于考慮如下系統(tǒng):
(8)
同理可知,周期解P5=(K1,0,0,0,0,0,0,0)T存在。當(dāng)1-θ1-e-C>0時(shí),周期解P6=(K1,S1,0,0,0,0,0,0)T存在,周期解P7=(K1,S1,E1,0,0,0,0,0)T,P8=(K1,S1,E1,I1,0,0,0,0)T都存在,其中,C=d1+(1-a1)r1+ρ1。
3 周期解的穩(wěn)定性
下面考慮系統(tǒng)的任意一個(gè)解P=(N1,S1,E1,I1,N2,S2,E2,I2)T的穩(wěn)定性。滿足如下條件的Φ(t)是8×8的矩陣函數(shù),
(9)
其中,
(10)
式中,
β12I2+ρ1],a24=-S1β11-ρ1,
β22I2+ρ2],
a68=-S2β22-ρ2,a76=β21I1+β22I2,
(11)
令M=BΦ(k),由Floquet定理知,當(dāng)M的特征值都小于1時(shí),系統(tǒng)的周期解是局部漸近穩(wěn)定的。
定理1 對(duì)于系統(tǒng)(3)和(4)來(lái)說(shuō),有以下結(jié)論成立:
(1) 周期解P0=(0,0,0,0,0,0,0,0)T是不穩(wěn)定的;
(2) 當(dāng)r1-mK2<0時(shí),周期解P1=(0,0,0,0,K2,0,0,0)T,P2=(0,0,0,0,K2,S2,0,0)T,P3=(0,0,0,0,K2,S2,E2,0)T是局部漸近穩(wěn)定的;
(3) 當(dāng)r1-mK2<0,ρ2=0和δ2=0時(shí),周期解P4=(0,0,0,0,K2,S2,E2,I2)T是局部漸近穩(wěn)定的。
證明 (1) 在周期解P0=(0,0,0,0,0,0,0,0)T處,有
其中,m21=(1-θ1)e(b1+ρ1)t,
m22=(1-θ1)e-(d1+ρ1)t,m65=(1-θ2)e(b2+ρ2)t,
m66=(1-θ2)e-(d2+ρ1)t,m68=(1-θ2)e-ρ2t。
M的特征值λ1=er1t>1,
λ2=(1-θ1)e-(d1+ρ1)t<1,所以,周期解P0是不穩(wěn)定的。
(2) 在周期解P1=(0,0,0,0,K2,0,0,0)T處,有
其中,m21=(1-θ1)e(b1+ρ1)t,
m22=(1-θ1)e-(d1+mK2+ρ1)t,
m23=(1-θ1)e-ρ1t,m24=(1-θ1)e-ρ1t,
m33=e-(d1+mK2+δ1)t,m44=e-(d1+mK2+γ1)t,
m65=(1-θ2)e(b2-2a2r2+ρ2)t,
m66=(1-θ2)e-[d2+(1-a2)r2+ρ2]t,
m88=e-[d2+(1-a2)r2+γ2]t。
M的特征值為
λ1=e(r1-mK2)t,
λ2=(1-θ1)e-(d1+mK2+ρ1)t,
λ3=e-(d1+mK2+δ1)t,λ4=e-(d1+mK2+γ1)t,
λ5=e-r2t,λ6=(1-θ2)e-[d2+(1-a2)r2+ρ2]t,
λ7=e-[d2+(1-a2)r2+δ2]t,λ8=e-[d2+(1-a2)r2+γ2]t。
當(dāng)r1-mK2<0時(shí),有λ1=e(r1-mK2)t<1,M所有的特征值均小于1,即周期解P1是局部漸近穩(wěn)定的。
同理,在周期解P2=(0,0,0,0,K2,S2,0,0)T處,當(dāng)r1-mK2<0時(shí),有λ1=e(r1-mK2)t<1,M所有的特征值均小于1,則周期解P2是局部漸近穩(wěn)定的。在周期解P3=(0,0,0,0,K2,S2,E2,0)T處,當(dāng)r1-mK2<0時(shí),有λ1=e(r1-mK2)t<1,M所有的特征值均小于1,所以周期解P3也是局部漸近穩(wěn)定的。在周期解P4=(0,0,0,0,K2,S2,E2,I2)T處,當(dāng)r1-mK2<0,ρ2=0且δ2=0成立時(shí),可以得到矩陣M的特征值均小于1。因此周期解P4是局部漸近穩(wěn)定的。
類似于定理1,有定理2成立:
定理2 系統(tǒng)(3)和(4)在滿足一定條件下,系統(tǒng)的周期解P5=(K1,0,0,0,0,0,0,0)T,P6=(K1,E1,0,0,0,0,0,0)T,P7=(K1,E1,S1,0,0,0,0,0)T,P8=(K1,E1,S1,I1,0,0,0,0)T均為局部漸近穩(wěn)定的。
4 總結(jié)
本文建立了兩種群相互競(jìng)爭(zhēng)的具有脈沖接種的傳染病模型,分析了模型周期解的存在性,證明了在滿足一定條件下,周期解P1,P2,P3,P4均為局部漸近穩(wěn)定的。這說(shuō)明,脈沖接種對(duì)傳染病的控制起著很大的作用,這為控制傳染病提供了一種方法。
[1]ZhangXiaobing,HuoHaifeng,XiangHong,etal..AnSIRSepidemicmodelwithpulsevaccinationandnon-monotonicincidencerate[J].NonlinearAnalysis:HybirdSystem, 2013, 8: 13-21.
[2]PangGuoping,ChenLansun.AdelayedSIRSepidemicmodelwithpulsevaccination[J].ScienceDirectChaos,SolitonsandFractal, 2007, 34: 1629-1635.
[3]T.Zhang,Z.Teng.PulsevaccinationdelayedSEIRSepidemicmodelwithsaturationincidence[J].AppliedMathematicalModelling, 2008, 32(7): 1403-1416.
[4]ZhaoZhong,ChenLansun,SongXinyu.ImpulsivevaccinationofSEIRepidemicmodelwithtimedelayandnonlinearincidencerate[J].MathematicalandComputerinSimulation, 2008, 79(3): 500-510.
[5]XiangZhongyi,LongDan,SongXinyu.AdelayedLotka-Volteramodelbirthpulseandimpulsiveeffectatdifferentmomentontheprey[J].AppliedMathematicsandComputation, 2013, 219(20): 10263-10270.
[6] 韓麗濤, 馬知恩, 師潭. 兩種群相互競(jìng)爭(zhēng)的具有標(biāo)準(zhǔn)傳染率的SIS傳染病模型[J]. 工程數(shù)學(xué)學(xué)報(bào), 2003, 20(4): 70-74.
[7] 韓麗濤. 兩種群相互競(jìng)爭(zhēng)的具有脈沖出生率的SIS傳染病模型[J]. 生物數(shù)學(xué)學(xué)報(bào), 2006, 21(2): 237-246.
[8] 宋云娜. 兩種群相互競(jìng)爭(zhēng)具有脈沖預(yù)防接種的SIR傳染病模型[J]. 科學(xué)技術(shù)與工程, 2012, 12(17): 4091- 4094.
[9] 徐文雄, 張?zhí)? 徐宗本. 兩種群相互競(jìng)爭(zhēng)的高維SEIR傳染病模型全局漸進(jìn)穩(wěn)定性[J]. 純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué), 2008, 24(2): 209-219.
SEIR Epidemic Model of Two Competitive Species with Pulse Vaccination
ZHOU Wen, HOU Gao-mei
(College of Mathematics and Computer Science, Anhui Normal University, Wuhu 241000, China)
An SEIR epidemic model of two competitive species with pulse vaccination is studied. We discuss the existence of periodic solution and prove that stability of periodic solution by using the Floquet theorem. The results demonstrated that periodic solutions are local asymptotic stable with satisfied fixed condition.
competitive model, pulse vaccination, periodic solution, stability
2015-03-24
項(xiàng)目名稱:國(guó)家自然科學(xué)基金(11302002)和安徽高校省級(jí)優(yōu)秀青年人才基金重點(diǎn)項(xiàng)目(2011SQRL022ZD)。
周文,女,安徽桐城人,安徽師范大學(xué)數(shù)計(jì)學(xué)院副教授,研究方向?yàn)樯飻?shù)學(xué);侯高梅,女,安徽阜陽(yáng)人,安徽師范大學(xué)數(shù)計(jì)學(xué)院碩士研究生,研究方向?yàn)樯飻?shù)學(xué)。
時(shí)間:2016-1-5 13:01 網(wǎng)絡(luò)出版地址:http://www.cnki.net/kcms/detail/34.1150.N.20160105.1301.002.html
O175.1
A
1007-4260(2015)04-0007-05
10.13757/j.cnki.cn34-1150/n.2015.04.002

