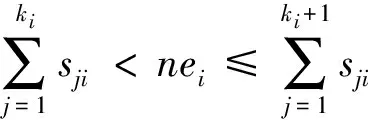數域上矩陣公分母的一些基本性質
王 禮 想
(安慶師范學院 數學與計算科學學院,安徽 安慶 246133)
數域上矩陣公分母的一些基本性質
王 禮 想
(安慶師范學院 數學與計算科學學院,安徽 安慶 246133)
文章引入了數域上矩陣公分母的概念,并且討論了數域上特殊線性群中矩陣公分母的一些基本性質。在數域的整數環是主理想環的特殊情況下,研究了最小公分母滿足的一些重要條件。
整數環;K-矩陣;Ok-矩陣;公分母
在研究數域K上的矩陣(以下簡稱K-矩陣)A(本文總假設A不是零矩陣)時,常把它與K的代數整數環Ok上的一個矩陣(以下簡稱Ok-矩陣)B建立關系,其中常用的方法:給A乘以Ok中的一個適當的代數整數α,使得B=αA是Ok-矩陣,顯然這樣的α不唯一,易驗證集合QA:={α∈Ok|αA是Ok-矩陣}是Ok的一個理想。
定義1 稱上述理想QA為矩陣A在域K上的公分母。如果QA是主理想,則把QA的任意生成元稱為A在域K上的一個最小公分母。
注1 在不致混淆的情況下,上述概念總是簡稱為A的公分母及A的最小公分母。特別地,在K是有理數域Q,Ok是有理整數環Z的情況下,熟知存在正整數n使得QA=(n),所以在此情況下,總是選擇n作為A的最小公分母。
在數域為有理數域這一特殊情況下,作為公分母這一概念的應用,文獻[4]中研究了在P∈SL(2,Q),且q級主同余子群Γq的共軛子群PΓqP-1為SL(2,Z)的子群時,P的最小公分母的如何取值的問題。文中有關模論的基本知識可參考文獻[1-2],代數數域的內容可參考文獻[3,5]。
本文主要是考慮數域K上n階特殊線性群SL(n,K)中矩陣公分母的一些基本性質。
定義2 給定K-矩陣A,稱A的一切元素在K中生成的分式理想IA為A的理想。
根據數域中分式理想的定義以及基本性質,下面命題1是顯然的。
命題2 給定n階K-矩陣A,B,AB乘積的公分母QAB整除QAQB。
證明 任取ω∈QA,θ∈QB,(ωθ)·(AB)=(ωA)·(θB) 是Ok-矩陣,而QAQB是包含一切ωθ的最小理想,即得QAQB?QAB。

證明 設Sn是對稱群,sgnσ是置換的符號,即sgnσ=1僅當σ是偶置換,否則sgnσ=-1。因A是SL(n,K)中矩陣,故其行列式為

命題5n階K-矩陣A∈SL(n,K)乘以SL(n,Ok)中一個矩陣后,公分母不變。
證明 由于A乘以可逆矩陣B∈SL(n,Ok)后的理想IAB?IA,當然I(AB)B-1?IAB,即IA=IAB,再由命題3即得。
下面主要是討論當Ok是主理想環時,最小公分母滿足的一些重要條件。這里除非特別說明,總是假設Ok是主理想環。由定義2知,用最小公分母代替公分母來討論是方便的。以下稱Ok中某一可逆元為單位,相差Ok中一個單位的兩元α,β稱為相伴。
命題6 給定K-矩陣A∈SL(n,K),非零元π∈Ok是A的一個最小公分母當且僅當矩陣B=πA的理想IB=Ok,即B的所有元素的最大公因子與1相伴。
證明 必要性。由于Ok是主理想環,且B的理想IB?Ok,因此存在非零元θ∈Ok使得IB=(θ)。因此C=θ-1B是Ok-矩陣,即存在α∈Ok,使得detC=α,故θn·α=detB=det(πA)=πn,即θn整除πn。如果θ,π的最大公因子與1相伴,則θ是單位,即證;否則存在Ok中不可約元ω同時整除θ,π,且是π的真因子,有πω-1∈IA=(π),矛盾。
充分性。設QA=(β)。由IB=Ok,則B=πA必然是Ok-矩陣,即π∈QA,故存在υ∈Ok,使得π=βυ。有必要性C=βA的理想IC=Ok,所以Ok=υOk,即υ是Ok的一個單位,而π是一個最小公分母。
根據模論的知識[1],對于主理想整環Ok上的矩陣有下面重要結論:
定理1 對于Ok上任意n階非零矩陣A,存在U,V,P,Q∈SL(n,Ok),使得UA為上三角形矩陣,AV為下三角形矩陣,而PAQ為對角形矩陣D:
D=diag(d1,d2,…,dr,0,…,0)
(1)
其中d1(1≤i≤r)是Ok中一組非零元,且滿足整除關系d1|d2|…|dr。進一步,這些di在Ok中元素相伴的意義下是唯一的。
注2 定理1中di稱為A的第i個不變因子。若A∈SL(n,K),則乘以它的最小公分母α,可知存在P,Q∈SL(n,Ok),使得B=αA可以化為(1)式的形狀,且r=n。故
G=PAQ=α-1diag(d1,d2,…,dn)
(2)
再由命題3與命題5知,G的最小公分母也是α,d1是Ok中的一個單位。而且由于detG=1,所以d1d2…dn=αn。由此可以討論Ok是主理想環時,命題2中,QAB何時與QAQB相等。
命題7 給定A,B∈SL(n,K),α,β分別是A,B的最小公分母。如果α,β互素,則乘積AB的最小公分母與αβ相伴,即QAB=QAQB。
證明 對矩陣A,設P,Q∈SL(n,Ok)滿足(2)式。這樣由命題5知AB與PAB公分母相同,由定理1知,
PAB=PAQ(Q-1B)=
α-1diag(d1,d2,…,dn)(Q-1B)
(3)
其中d1,d2,…,dn=αn。
再由命題5知,Q-1B與B公分母相同。由定理1設V∈SL(n,Ok),使得(Q-1B)V為下三角形,當然仍與B公分母相同。設
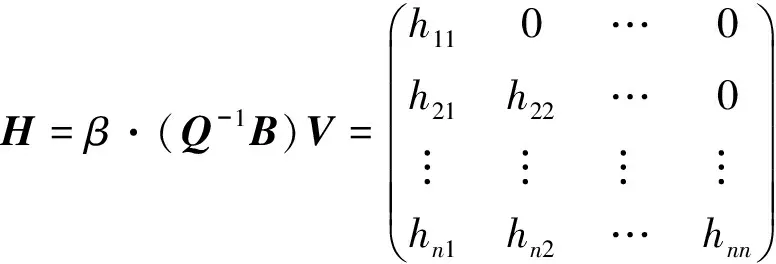
其中對于1≤i,j≤n,hij∈Ok并且h11h22…hnn=βn。由(3)式可得:
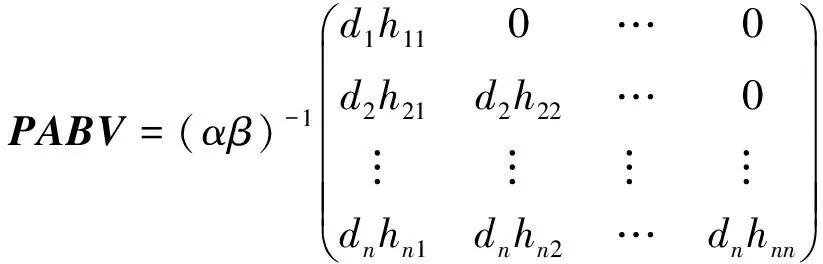
設H的第j行元的一個最大公因子hj,顯然hj整除hjj。
由命題6知d1,d2,…,dn與h1,h2,…,hn兩組元素的最大公因子都與1相伴,下面證明d1h1,d2h2,…,dnhn的最大公因子也與1相伴。
反證法 假設有素元p同時整除這n個元,則可知p至少整除一個di和一個hj,否則由素元的性質,p將整除所有di或hj,這與它們的最大公因子是單位相矛盾。而由此導致p整除d1d2…dn=αn,但是由hj的定義,h1h2…hn整除h11h22…hnn=βn,這樣p同時整除αn與βn,這與α,β互素矛盾,即證AB最小公分母與αβ相伴。
下面證明命題7對應的逆命題也正確。
命題8 設C∈SL(n,K),γ=αβ是其一個最小公分母,則存在A,B∈SL(n,K),滿足C=AB,且A,B的最小公分母分別與α,β相伴。
證明 取P,Q∈SL(n,Ok),使得
PCQ=γ-1diag(d1,d2,…,dn),
如果γ是單位,則結果顯然,因此可令γ,α,β分解式分別為

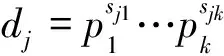
如果ei=0,則對整數1≤j≤n,令αji=1。
如果ei≠0,因為nhi≥nei,且s1i=0,故存在0 此時令 A=α-1P-1diag(α1,α2,…,αn), B=β-1diag(β1,β2,…,βn)Q-1, 容易驗證A,B滿足所求。 命題9 給定A∈SL(n,K),α是A的最小公分母,dn是αA的第n個不變因子,則α整除dn,且A-1的最小公分母與dnα-1相伴。 證明 取P,Q∈SL(n,Ok)使得(2)式成立。設p是α的一個素因子。如果對于非負整數f,pf整除α,則pnf整除αn。如果pf不能整除dn,則d1|d2|…|dr也不能整除di,但是d1是單位,因此由d1d2…dn=αn得p(n-1)f不整除αn,矛盾,即α整除dn。 對后一斷言,由(2)式得: 由α整除dn得G-1的最小公分母與dnα-1相伴,再由命題5即得。 [1]T. S. Blyth.Module Theory:An Approach to Linear Algebra [M]. Oxford: Clarendon Press, 1977. [2]J. J. Rotman. 高等近世代數[M]. 章亮, 譯. 北京: 機械工業出版社, 2007:483-490. [3]馮克勤. 代數數論[M]. 北京: 科學出版社, 2001. [4]孫廣人. 主同余子群的Γ(n)-正規化子[J]. 安慶師范學院學報(自然科學版), 2013, 19(4), 5-7. [5]張賢科. 代數數論導引[M]. 2版. 北京: 高等教育出版社, 2006. On the Common Denominator of a Matrix over Some Number Field WANG Li-xiang (Department of Mathematics, Anqing Teachers College, Anqing 246133, China) The notion common denominator of a matrix over some number field is introduced in this paper. Some basic facts are cleared when the matrix is belonging to the special linear group over a given number field. When the integer ring of number field is a principal ideal domain, several fundamental properties on minimum common denominator are stated. integer ring,K-matrix,Ok-matrix, common denominator 2015-05-20 安慶師范學院青年科研基金(KJ201414)。 王禮想,女,安徽淮北人,碩士,安慶師范學院數學與計算科學學院講師,研究方向為數字圖像處理。 時間:2016-1-5 13:01 網絡出版地址:http://www.cnki.net/kcms/detail/34.1150.N.20160105.1301.005.html O152.3 A 1007-4260(2015)04-0016-03 10.13757/j.cnki.cn34-1150/n.2015.04.005