分布式全相參雷達相參性能分析

宋 靖張劍云

(電子工程學院 合肥 230037)

分布式全相參雷達相參性能分析

宋 靖*張劍云

(電子工程學院 合肥 230037)

該文針對多脈沖發射協同結構的分布式全相參雷達，首先建立了全相參模式下的信號模型，然后推導了輸出信噪比增益(oSNRg)的解析式，并基于相干參數估計的克拉美-羅界(CRB)，利用多項式擬合，獲得了oSNRg上界的數值解。結果表明：增加發射天線數或脈沖數能夠提高oSNRg；而增加接收天線數能否提高oSNRg取決于輸入信噪比大小，輸入信噪比較大時則oSNRg隨之提高，較小時反而隨之下降。最后的仿真實驗驗證了研究結論的正確性。

雷達；分布式；全相參；輸出信噪比增益；多項式擬合

1 引言

分布式全相參雷達是繼多輸入多輸出(MIMO)雷達之后出現的一種新體制雷達，它解決了大口徑雷達難以機動部署和造價昂貴等問題，是下一代雷達發展的技術方向。該雷達的主要特點包括：多部機動式單元雷達或天線分散布設，通過對多部雷達回波進行信號級相參合成，等效形成一個大威力探測雷達。其關鍵能力包括：具有較高靈敏度，適用于遠距離搜索、跟蹤和目標識別，同時滿足機動部署能力。分布式全相參雷達先后工作于兩種典型模式：MIMO模式和全相參模式。首先在MIMO模式下發射一組正交信號，分別估計出收發端的相干參數；然后雷達轉換到全相參模式，發射一組相同信號，利用估計的相干參數分別對收發端進行精確補償和控制，從而實現收發全相參。全相參模式是其所獨有的常態化模式，是MIMO雷達所不具備和無法實現的。根據收發天線數配置不同，分布式全相參雷達主要分為主輔(master-slave)和協同(cooperative)結構，前者僅利用一部單元雷達接收信號，所需處理數據量小；而后者利用全部單元雷達接收信號，能夠獲得更好的相干參數估計性能。

國外主要是美國林肯實驗室對該技術做了大量研究[1- 5]。國內目前對該技術的研究尚屬起步階段，但是其潛在優勢和應用前景已引起各大高校和研究所的關注[6- 11]。文獻[5]定義了全相參模式下輸出信噪比增益(output Signal-to-Noise Ratio gain, oSNRg)，但未能研究其解析式。文獻[6,7]研究了時間和相位同步問題，以及相位差跟蹤技術。文獻[8]介紹了技術背景和發展現狀。文獻[9]針對收發天線分置的一般結構，考慮單脈沖發射，推導了相干參數估計的克拉美-羅界(Cramer-Rao Bound, CRB)閉式解，并基于CRB分析了相參處理性能。文獻[10]針對主輔結構，將單脈沖拓展到多脈沖，研究了相干參數估計和相參處理性能。文獻[11]針對部分收發共置，首先建立了“全發任意收”的混合結構，它是包含主輔結構和協同結構的更一般結構，然后在發射多脈沖條件下推導了相干參數估計CRB閉式解，但是未能進一步分析相參處理性能。值得指出的是，MIMO雷達參數估計已得到學術界廣泛關注[12- 17]，盡管其與分布式全相參雷達參數估計問題相似，但是二者存在本質區別：首先，待估的目標參數不同，在前者中常見的有位置和速度估計，而在后者中需要估計的是各天線間時延差和相位差等相干參數；其次，待估目標參數數目與收發天線數的關系不同，在前者中往往一定，而在后者中隨收發天線數的增加而增加；最后，針對相位參數的處理方式也不同，在前者中通常被看作隨機變量，而在后者中則作為確定性未知參量，是需要估計和補償的重要參數。

相干參數估計是實現各單元雷達間相參處理的前提，但并非最終目的。相參性能分析是分布式全相參雷達的一個重要問題。本文針對協同結構的分布式全相參雷達，在多脈沖發射條件下，研究了收發天線數及脈沖數對相參性能的影響。首先建立了MIMO模式和全相參模式下的分布式全相參雷達信號模型；然后推導了oSNRg的解析式，并基于文獻[11]獲得的相干參數估計CRB，利用多項式擬合獲得oSNRg上界的數值解。

2 信號模型

2.1 MIMO模式信號模型

由K個發射天線，L(1≤L≤K)個接收天線和1個處理中心組成的混合結構的分布式全相參雷達[11]如圖1所示，其中接收天線與部分發射天線共置。顯然，若L=1則為主輔結構，L=K則為協同結構。假設發射一組正交窄帶信號經上變頻，發射信號復包絡可表示為sk(t) ej2πfc t+jφkt，其中fc為載頻，為發射天線Tk的初始相位。

假設空間存在一個各向同性散射點目標，且確定性復散射系數為ξ。目標相對于各單元雷達的距離變化率為常數，且在觀測時間內不離開雷達距離分辨單元。定義R˙k和Rk,0分別為目標相對于第k部雷達的距離變化率和初始距離，則第n個脈沖時刻，目標相對于第k部雷達的距離可表示為Rk, n=Rk ,0其中N為發射脈沖總數。對于第lk個收發路徑，第n個脈沖的傳播時間可表示為

圖1 混合結構的分布式全相參雷達

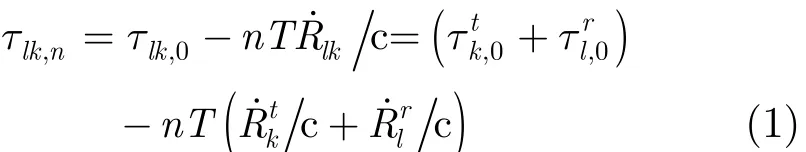
式中，φlr為接收天線Rl的初始相位，φlk=2πfcTR˙lk/c為第lk個路徑的多普勒頻移，wln(t)為Rl接收第n個脈沖的噪聲。假設wln(t)是空間和時間獨立的，且wln

(t)在時域上是均值為零、方差為σw2的復白高

斯過程。τlk,0,τk

t,0和τlr,0分別寫作τlk,τkt和τlr。選定(T/R)1為發射或接收參考天線，且定義ξ=從而式(2)可改寫為

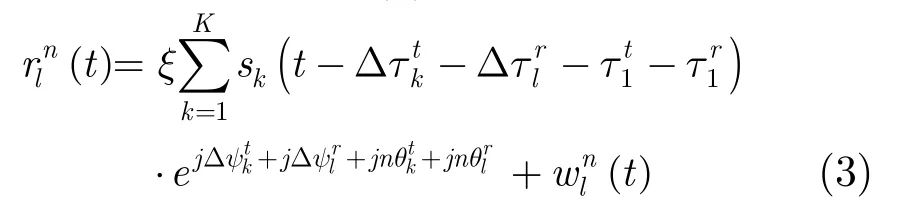
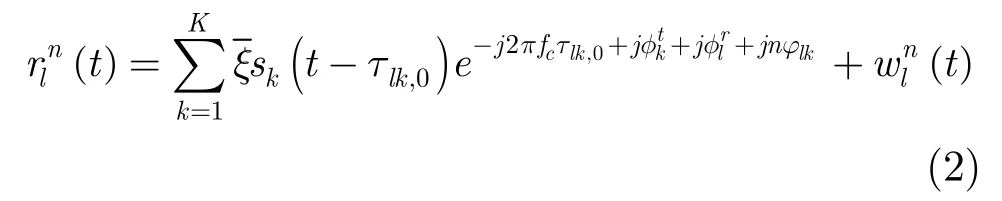
2.2 全相參模式信號模型

假設雷達由MIMO模式轉換到全相參模式時，相干參數估計是穩健的。定義各相干參數估計值為相位和多普勒頻移補償后，Tk發射的第n個脈沖經上變頻可表示為

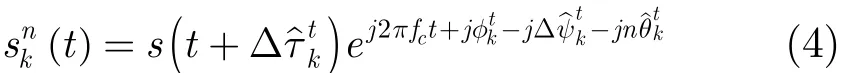
同理，在接收端經補償后，Rl接收的第n個脈沖經過下變頻可表示為

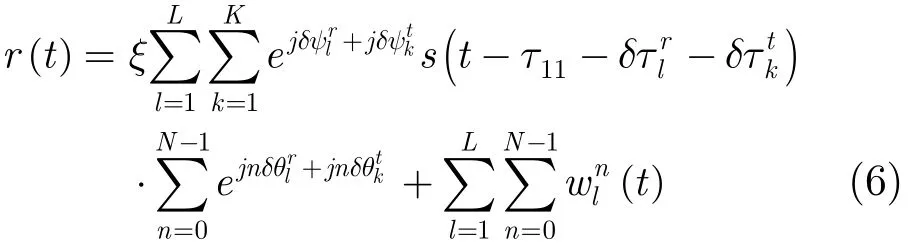
3 相參性能分析

3.1 oSNRg解析式

選擇大時寬帶寬積的線性調頻信號作為發射信號，經脈沖壓縮后可表示為

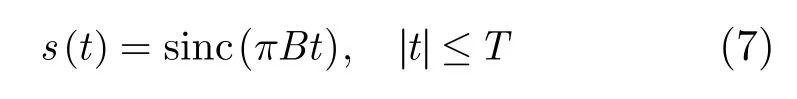
式中B為信號帶寬。根據式(6)可知，在τ11時刻的樣本信號具有最大平均功率，因此不含噪聲的樣本信號的平均功率Pso可表示為

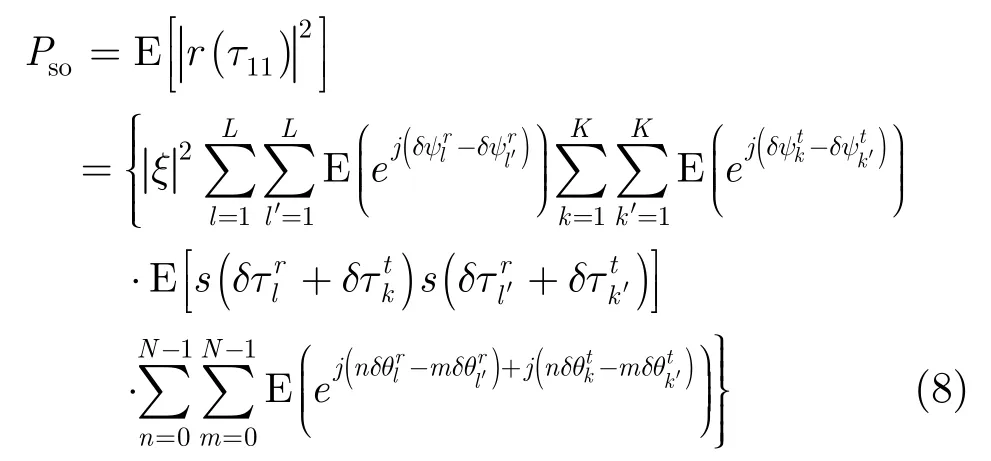
為簡化分析過程并給出直觀有用的結論，只考慮協同結構的oSNRg。由于L=K，因此根據式(8)，協同結構的輸出平均功率

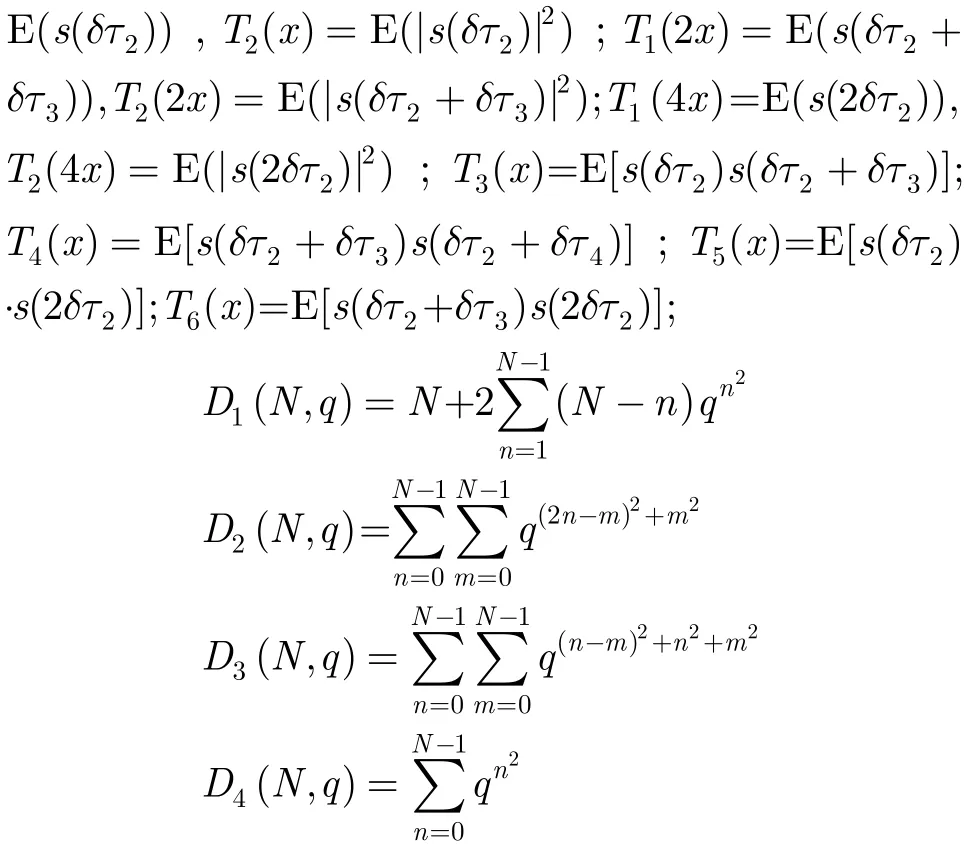
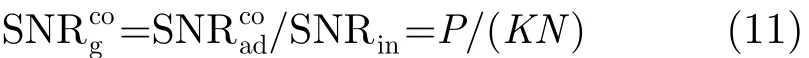
若無特別說明，下文中“oSNRg”均指其上界。根據式(11)可得以下結論：

K和N。

(3)相比于相位差和多普勒頻移，高精度的時延差估計更容易獲得。當且K為發射天線數(仿真實驗圖4說明這一點)。

主輔和協同結構是分布式全相參雷達的兩種典型結構，將主輔[10]和協同結構的oSNRg對比列于表1。由表1可知：較主輔結構，協同結構由于利用全部K個天線接收信號，所以當時，其oSNRg提高K倍；當時，其oSNRg下降至1/K；當兩者均為K，且K為發射天線數。

表1 主輔與協同結構對應的oSNRg

3.2 oSNRg數值解

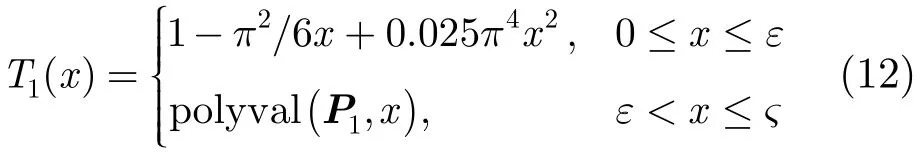
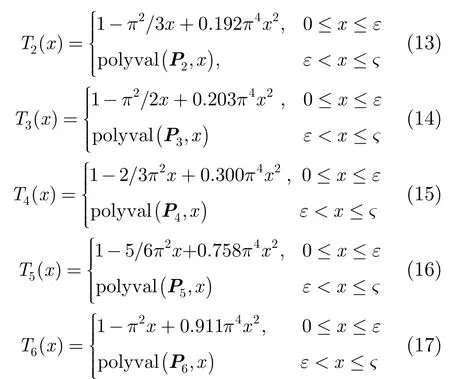
根據式(7)可知，s( δτ2)的泰勒展開式為可用低階泰勒展開式近似表示，否則基于蒙特卡洛仿真，利用多項式擬合近似表示。具體地，式(12)～式(17)中，polyval表示多項式求值運算，ε 和?分別為擬合區間的下界和上界，仿真實驗中分別取0.02和50。Pi(i=1,2,…,6)為擬合系數向量，由實驗獲得(實驗中最高階數取25)。同理，T1(2x)(或T1(4x))和T2(2x)(或T2(4x))分別代入式(12)和式(13)即可獲得對應的表達式。

4 仿真結果與分析

實驗1 N不同時對應的oSNRg

選擇B=100 MHz, SNRin=-22～30 dB, N = [1,4,8], K=2。當min(SNRin)=-22 dB , min( N) =1時，x滿足3.2節的擬合區間要求。

圖2展示了時延補償誤差對協同結構oSNRg的影響：當SNRin越小時，影響越顯著；相比于N=1, N=4(或N=8)對應的理想oSNRg提高6 dB(或9 dB)。

考慮時延補償誤差時，對比協同與主輔結構的oSNRg，如圖3所示。由圖3可知，在同一N時，協同結構的理想oSNRg較主輔結構提高3 dB(或2 倍)；當SNRin較低時，由于采用單天線接收，所以主輔結構的oSNRg趨于0 dB，而協同結構由于采用2個天線接收，所以其oSNRg趨于-3 dB(或者1 2)。根據圖3，對比協同與主輔結構的oSNRg，以N=1為例，當SNRin＞-9 dB 時，前者大于后者；當SNRin＜-9 dB 時，前者小于后者。盡管多天線接收能夠提高相干參數估計精度，但是引入的噪聲功率也與接收天線數成正比，所以從提高oSNRg的角度考慮，并不是接收天線越多越有利，而是決定于SNRin閾值。此外隨著N的增加，由于相干參數估計精度提高，對應的SNRin閾值降低。

實驗2 K不同時對應的oSNRg

選擇N=2, SNRin=-25～30 dB , B=100 MHz,K=[2,4,8]。同理，當min(SNRin)=-25 dB, min(K)=2時，x滿足3.2節的擬合區間要求。

不考慮時延補償誤差，圖4展示了協同與主輔結構的oSNRg隨SNRin的變化曲線。由圖4可知，在同一K時，協同結構的理想oSNRg較主輔結構提高K倍；當SNRin趨于無窮小時=∞)，兩者趨于一致，且等于K。

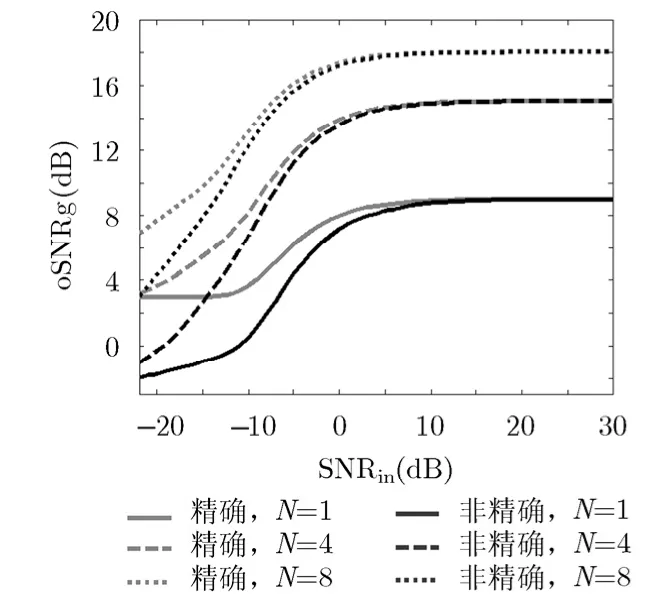
圖2 時延補償精確與否對oSNRg的影響

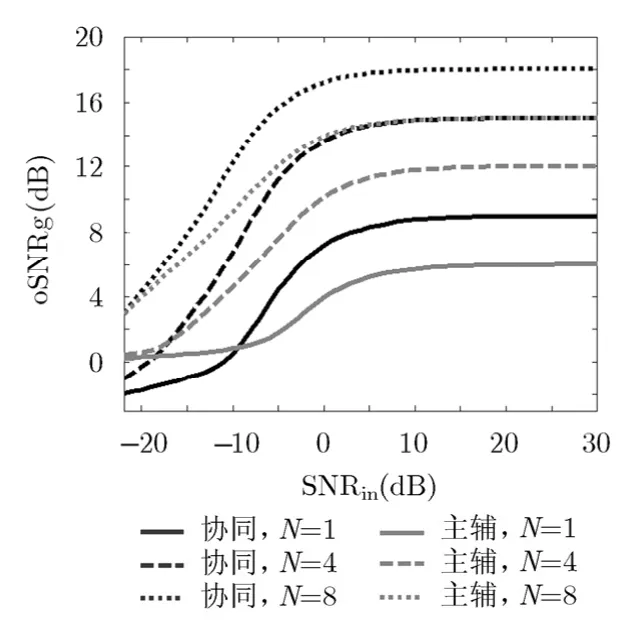
圖3 不同脈沖數對應的oSNRg 隨SNRin的變化曲線

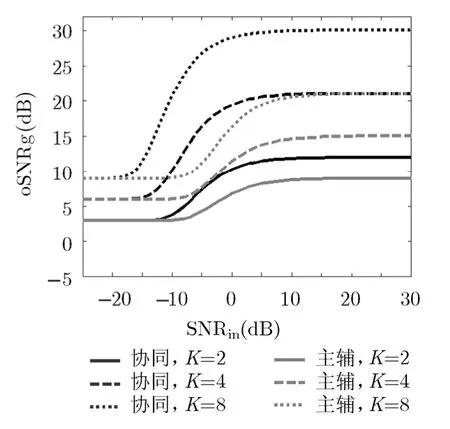
圖4 時延精確補償時的oSNRg 隨SNRin的變化曲線

考慮時延補償誤差時，圖5展示了協同與主輔結構oSNRg隨SNRin的變化曲線。結論與圖3類似，且隨著K的增加，對應的SNRin閾值降低。特別地，在SNRin∈[-25,30] dB 時，主輔結構對應的oSNRg隨著發射天線數K的增加而提高。

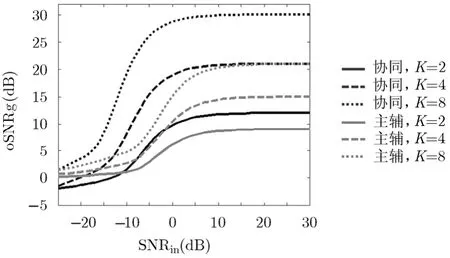
圖5 不同發射天線數對應的oSNRg隨SNRin的變化曲線

5 結束語

oSNRg是衡量分布式全相參雷達性能的重要指標。本文針對多脈沖發射協同結構的分布式全相參雷達，考慮時延、相位和多普勒頻移補償誤差同時存在時，推導了oSNRg的解析式，并基于相干參數估計CRB獲得oSNRg的數值解。理論和實驗結果表明，oSNRg隨著脈沖數或發射天線數的增加而提高。然而增加接收天線數能否提高oSNRg取決于輸入信噪比大小：輸入信噪比較大時，oSNRg隨接收天線數增加而提高，輸入信噪比較小時，oSNRg隨接收天線數增加反而下降。本文主要基于相干參數估計CRB獲得了輸出信噪比增益的上界。為更好地指導實際工程應用，下一步將結合具體的相干參數估計算法和輸出信噪比增益，研究分布式全相參雷達的相參處理性能。

[1] Ahlgren G W. Next generation radar concept definition team final report[R]. MIT Lincoln Laboratory, 2003.

[2] Cuomo K M, Coutts S D, McHarg J C, et al.. Wideband aperture coherence processing for next generation radar (NexGen)[R]. MIT Lincoln Laboratory, 2004: 11-16.

[3] Coutts S D, Cuomo K M, McHarg J C, et al.. Distributed coherent aperture measurements for next generation BMD radar[C]. Fourth IEEE Workshop on Sensor Array and Multichannel Processing, Walthma, MA, USA, 2006: 390-393.

[4] Brookner E. Phased-array and radar astounding breakthroughs-an update[C]. IEEE Radar Conference, Boston, MA, USA, 2007: 37-42.

[5] Fletcher A and Robey F. Performance bounds for adaptive coherence of sparse array radar[C]. 11th Conference Adaptive Sensors Array Processing, MIT Lincoln Laboratory, Lexington, MA, USA, 2003: 290-293.

[6] 曾濤, 殷丕磊, 楊小鵬, 等. 分布式全相參雷達系統時間與相位同步方案研究[J]. 雷達學報, 2013, 2(1): 105-110. Zeng Tao, Yin Pi-lei, Yang Xiao-peng, et al.. Time and phase synchronization for distributed aperture coherent radar[J]. Journal of Radars, 2013, 2(1): 105-110.

[7] 殷丕磊, 楊小鵬, 曾濤. 分布式全相參雷達的相位差跟蹤技術[J]. 信號處理, 2013, 29(3): 313-318. Yin Pi-lei, Yang Xiao-peng, and Zeng Tao. Tracking technology of phase difference for distributed aperture radar [J]. Journal of Signal Processing, 2013, 29(3): 313-318.

[8] Gao Hong-wei, Cao Zhe, Wen Shu-liang, et al.. Study on distributed aperture coherence synthesizing radar with several experiment results[C]. IEEE Radar Conference, Xi’an, China, 2011: 84-86.

[9] Sun P L, Tang J, He Q, et al.. Cramer-Rao bound of parameters estimation and coherence performance for next generation radar[J]. IET Radar, Sonar & Navigation, 2013,7(5): 553-567.

[10] Tang X W, Tang J, He Q, et al.. Cramer-Rao bounds and coherence performance analysis for next generation radar with pulse trains[J]. Sensor, 2013, 13(1): 5347-5367.

[11] 宋靖, 張劍云, 鄭志東, 等. 分布式全相參雷達相干參數估計性能[J]. 電子與信息學報, 2014, 36(8): 1926-1931. Song Jing, Zhang Jian-yun, Zheng Zhi-dong, et al.. Coherent parameters estimation performance for distributed aperture coherent radar[J]. Journal of Electronics & Information Technology, 2014, 36(8): 1926-1931.

[12] Godrich H, Haimovich A M, and Blum R S. Target localization accuracy gain in MIMO radar-based systems[J]. IEEE Transactions on Information and Theory, 2010, 56(6): 2783-2802.

[13] He Q, Blum R S, Godrich H, et al.. Target velocity estimation and antenna placement for MIMO radar with widely separated antennas[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(1): 79-100.

[14] He Q, Blum R S, and Haimovich A M. Noncoherent MIMO radar for location and velocity estimation: more antennas means better performance[J]. IEEE Transactions on Signal Processing, 2010, 58(7): 3661-3680.

[15] Wei C M, He Q, and Blum R S. Cramer-Rao bound for joint location and velocity estimation in multi-target non-coherent MIMO radars[C]. Proceedings of 44th Conference on Information Science Systems, Princeton, NJ, USA, 2010: 1-6. [16] He Q and Blum R S. Cramer-Rao bound for MIMO radar target localization with phase errors[J]. IEEE Signal Processing Letters, 2010, 17(1): 83-86.

[17] Godrich H and Haimovich A M. Localization performance of coherent MIMO radar systems subject to phase synchronization errors[C]. Proceeding of Fourth ISCCSP, Limassol, Cyprus, 2010: 1-5.

宋 靖： 男，1986年生，博士生，研究方向為MIMO雷達信號處理及分布式雷達技術.

張劍云： 男，1963年生，教授，博士生導師，研究方向為雷達及目標環境模擬、雷達信號處理、高速信號處理.

Coherence Performance Analysis for Distributed Aperture Coherent Radar

Song Jing Zhang Jian-yun
(Electronic Engineering Institute, Hefei 230037, China)

For distributed aperture coherent radar with cooperative architecture and pulse trains, the signal mode in fully coherent work mode is proposed firstly. Then the analysis formula of output Signal-to-Noise Ratio gain (oSNRg) is derived, and the performance bound of oSNRg is developed by using polynomial fitting based on Cramer-Rao Bounds (CRB) of coherence parameters estimation. It is concluded that more transmitters or pulses make higher oSNRg. However, as the number of receivers increase, if the input SNR is high sufficiently, the oSNRg will gradually improve; if not, it will worsen. Finally, numerical examples demonstrate the validity of the theoretical results.

Radar; Distributed aperture; Fully coherent; Output Signal-to-Noise Ratio gain (oSNRg); Polynomial fitting

TN958

A

1009-5896(2015)01-0009-06

10.11999/JEIT140202

2014-02-17收到，2014-07-23改回

國家自然科學基金(60702015)資助課題

*通信作者：宋靖 songjingpla@163.com