基于容腔動力學的分排渦扇發動機動態建模
牟春陽,李世中
(中北大學 機電工程學院,太原 030051)
0 引言
發動機數學模型是發動機性能等用數學表述的一種形式。由于發動機控制系統設計、控制系統數字仿真和半物理仿真等都要基于發動機非線性部件級模型展開[1~4],所以發動機建模是發動機控制系統研究的重要部分,只有所建立的數學模型能夠在全包線、全狀態下模擬真實發動機的工作情況,才能保證基于部件級模型的研究成果的有效性。為此早在20世紀70年代發動機數學模型的研究就引起的廣泛關注[5~7]。
建立發動機數學模型的方法有解析法和試驗法[8]。目前國內的發動機數學模型大多數為通過求解共同工作方程建立的部件級氣動熱力學模型或小偏差線性化模型,但這種方法有它的不足之處,由于發動機具有強非線性,只有初猜值在真實解附近,該方法才能保證迭代收斂。這在實際計算中保證全飛行包線內都收斂是很困難的。為解決部件級建模中解非線性方程組時的迭代問題,本文基于容腔動力學建立渦輪發動機的數學模型,認為動態時流量不再平衡,壓力隨流量變化而變化,并通過該數學模型各截面參數與試驗數據比對,驗證模型的準確性。
1 容腔動力學
一臺噴氣發動機包含眾多的小容腔,每一個小容腔可以存儲熱能和一定質量的空氣/燃氣。由于空氣和燃氣是連續介質,一個小容腔內的能量和質量動力學行為均是分布式系統,而小容腔的大小決定了用集中參數系統來近似容腔動力學的逼近程度。把空氣/燃氣通道的小容腔劃分的越小,則逼近越準確[8]。對于分排渦扇發動機,其容腔劃分如圖1灰色邊框區域。

圖1 分排渦扇發動機空氣和燃氣容腔
容腔內的質量存儲效應導致容腔內的壓力和溫度發生變化。這些變化是容腔內空氣或燃氣的壓力和溫度存在熱力學聯系的結果。考慮如圖2所示的單位空氣容腔。

圖2 空氣/燃氣單位容積
控制面內空氣(或燃氣)質量的變化率為:

容腔內的空氣以溫度T、壓力p和密度ρ來表征。假設空氣在標稱工作點附近為理想氣體,容腔內壓力的微小變化量為:

式中,V是控制面包圍的體積,為常量。上述方程對時間微分,得到:

因而容腔內壓力的變化率與溫度和質量的變化率相關。然而,由于上述方程右邊第一項要遠小于第二項,可以舍去第一項,這樣,上式中壓力項就近似正比于容腔內質量的變化率。

即:

2 分排渦扇發動機動態模型建模方法
分排渦扇發動機工作過程中,各部件之間滿足以下共同工作條件:
壓氣機與高壓渦輪之間空氣流量連續;
高壓渦輪與低壓渦輪之間燃氣流量連續;
低壓渦輪與噴管之間空氣流量連續;
風扇進口與發動機出口總流量連續;
高壓轉子功率平衡;
低壓轉子功率平衡。
根據容腔動力學描述,將每個流量連續共同工作條件對應一個容腔模塊,計算時根據容腔進出口截面流量差更新模型中相對應的壓力狀態;另外,轉子的功率平衡約束是一組描述發動機轉速動態變化的微分方程,根據轉子功率平衡方程,計算過程中可采用歐拉積分的方法對高低壓轉子轉速進行更新。
分排渦扇發動機動態模型可以表示成如下形式:

式(6)中,模型狀態x1,輸入變量u和輸出變量y分別為:

在給定的狀態、輸入條件下,通過發動機部件計算可以求得對應的發動機整機及各個部件性能參數。部件計算后,根據部件容腔模塊更新發動機動態模型中的壓力狀態參數,根據功率平衡方程更新高低壓轉子轉速。
分排渦扇發動機動態模型中將風扇后作為1號容腔模塊,由1號容腔更新風扇后總壓Pt2;在壓氣機與燃燒室之間加入2號容腔,由2號容腔更新壓氣機后總壓Pt3;在高低壓渦輪之間加入3號容腔,由3號容腔更新高壓渦輪后總壓Pt5;在低壓渦輪后與尾噴管之間加入4號容腔,由4號容腔更新低壓渦輪出口總壓Pt6。部件容腔的放置位置如圖3中所示。

圖3 分排渦扇發動機模型部件容腔位置示意圖
容腔計算:
1)風扇容腔
對風扇容腔效應進行計算:

其中,Tt2為風扇后總溫,VF為風扇處容腔體積,容腔入口流量WaFAN,in=Wa2,Wa2為風扇空氣流量,容腔出口流量WaFAN,out=Wa3+Wa82,Wa3為壓氣機空氣流量,Wa82為外涵道空氣流量。
2)壓氣機容腔
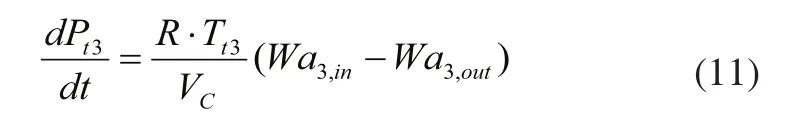
其中,Tt3為壓氣機后總溫,VC為壓氣機處容腔體積,Wa3,in為壓氣機空氣流量Wa3,Wa3,out=Wg5-Wf1為高壓渦輪燃氣流量減去主燃燒室燃油流量。
3)高壓渦輪容腔
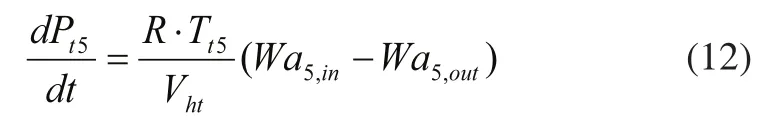
其中,Tt5為高壓渦輪后總溫,Vht為高壓渦輪處容腔體積,Wa5,in為高壓渦輪燃氣流量Wg5,Wa5,out為低壓渦輪燃氣流量Wg6。
4)低壓渦輪容腔

其中,Tt6為低壓渦輪后總溫,Vlt為低壓渦輪處容腔體積,Wa6,in為低壓渦輪部件空氣流量的計算結果Wg6,Wa6,out為尾噴管出口燃氣流量Wg81。
另外,考慮兩個轉子的動力學方程。
根據動能定理,高、低壓渦輪輸出功率與壓氣機、增壓級、風扇部件的消耗功率之間滿足:

上式中,η為渦輪軸的機械效率,J為轉子轉動慣量。
轉子轉速n與轉動角速度ω之間的換算關系為:

將式(16)帶入式(14)、式(15)中,整理可得描述發動機轉子功率平衡的微分方程:

3 仿真驗證
為保證動態模型程序的實時性,并使軟件在不同環境下具有良好的兼容性,采用標準C語言進行代碼編寫。根據發動機動態數學模型功能計算需求,按照“高內聚、低耦合”的模塊劃分原則,采用面向對象思想搭建發動機動態數學模型。發動機模型程序主要由16個子功能模塊組成,分別為氣動函數計算模塊、矩陣運算模塊、插值計算模塊、發動機尺寸模塊、發動機轉子模塊、發動機輸入模塊、進氣道計算模塊、風扇計算模塊、壓氣機計算模塊、燃燒室計算模塊、高壓渦輪計算模塊、低壓渦輪計算模塊、外涵道計算模塊、噴管計算模塊、容腔計算模塊和發動機上層組織模塊。
分排渦扇發動機動態模型程序模塊之間的組織關系如圖4所示。

圖4 分排渦扇發動機模型程序模塊組織關系
將模型封裝為MATLAB/Simulink中S函數,模型輸入為飛行高度H、馬赫數Ma和燃油流量wf,模型輸出為各截面特征參數,模型方框圖如圖5所示。

圖5 封裝為S函數的Simulink圖
模型的輸入為0高度0馬赫數,燃油輸入值為試驗數據,如圖6所示。

圖6 燃油流量
試驗數據與模型輸出對比如圖7~圖9所示。

圖7 高壓轉子轉速對比曲線

圖8 低壓轉子轉速對比曲線

圖9 壓氣機出口總壓對比曲線
綜上,模型仿真數據與試驗數據存在一定的差異(其中壓氣機出口總壓相差較大,約6%左右,高、低壓轉子轉速相差較小,約1%左右),其差異存在的主要原因是部件特性存在一定的誤差。
4 結論
分排渦扇發動機動態數學模型是進行發動機性能仿真分析和進行發動機控制系統設計、分析和數值驗證的重要基礎。本文詳細介紹了基于容腔動力學約束的非線性動態數學模型建模方法,該方法可以有效避免發動機性能計算中的迭代過程,具有更好的計算穩定性。文中通過仿真實例驗證了模型的收斂性。該模型是發動機實時動態仿真和基于在線實時模型的先進控制系統設計的基礎。
[1]Koenig R W,Fisbbaco L H.Geneng-A program for calculating design and off-design performance for turbojet and turbofan engines[R].NASA TND-6552,1972.
[2]Fisbbacb L H, Koenig R W.Geneng II-A program for calculating design and off-design performance of two- and three-spool turbofans with as many as three nozzles[R].NADA TND-6553,1972.
[3]陶金偉.航空發動機組態建模仿真技術研究[D].南京:南京航空航天大學,2009.12.
[4]鄒先權.渦軸發動機自適應模型的建立與魯棒控制[D].南京:南京航空航天大學,2008.12.
[5]于龍江,樸英.一種簡化算法的航空發動機全狀態數學模型[J].航空動力學報,2008,23(3):510-515.
[6]楊剛,孫健國,黃向華,等.一種不需要迭代的發動機輔助變量建模方法[J].航空動力學報,2003,18(2):289-294.
[7]夏超,王繼強,商國軍,等.基于Matlab/Simulink的航空發動機部件級建模與分析[J].航空發動機,2012,38(4):31-33.
[8]張新國,譯.飛機發動機控制——設計、系統分析和健康監視[M].北京:航空工業出版社,2011.

