接地導體圓筒內帶電正六棱柱的電場及系統的電容

王福謙

（長治學院 電子信息與物理系，山西 長治 046011）

接地導體圓筒內帶電正六棱柱的電場及系統的電容

王福謙

（長治學院 電子信息與物理系，山西 長治 046011）

利用數值保角變換，給出接地導體圓筒內帶電正六棱柱體電場的分布規律，繪制出其橫截面上的電場線與等勢線圖，并計算該導體系統單位長度的電容。

接地導體圓筒；帶電正六棱柱；數值保角變換；電場分布；電容

接地導體圓筒內帶電圓柱的電場分布及系統電容的分析，常見于有關“電磁場與電磁波”教材中，但對于接地圓筒內帶電正六棱柱的情形，其電場分布及單位長度電容量的討論，相關文獻還未見涉及。由于該系統橫截面上的正六邊形和圓不屬于同一族正交坐標系，因此嚴格地求解拉普拉斯方程十分困難，故其內部的電場分布和電容量，一般不能用常規解析法直接求解。為此，文章擬利用數值保角變換，研究接地導體圓筒內正六棱柱體電場的分布規律，繪制出其橫截面上的電場線與等勢線圖，并給出精度較高的該導體系統單位長度電容的計算公式。

1 內六棱柱-外圓筒橫截面的變換

將z平面上邊長為a正六邊形的外部變換為w平面上單位圓的外部的變換函數為：[1]

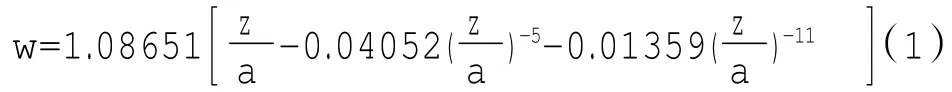
圖1為接地圓筒內帶電正六棱柱系統的橫截面，其內、外均為金屬導體。邊長和半徑分別為a和b，則由式（1）可實現該導體系統橫截面的變換。內正六邊形變換為單位圓，外圓變換為位于之間的具有與正六邊形相同對稱性的閉合曲線[見圖2中的閉合曲線，該曲線由式（1）通過MATLAB軟件繪制]，而r1、r2及其幾何平均半徑的數值如下：[1]

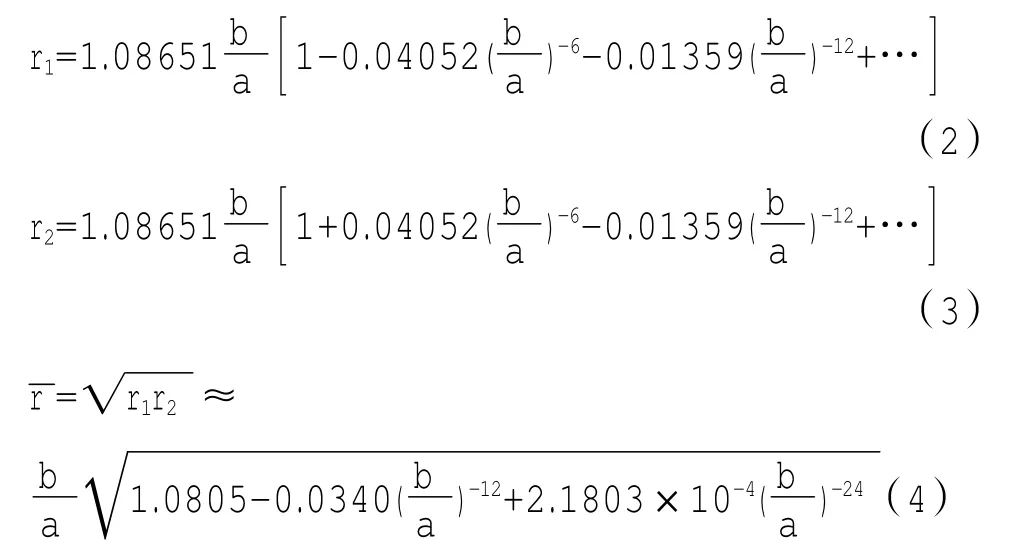
經上述數值保角變換后，z平面上的邊長a為的正六邊形和半徑為b的圓，就映射為w平面上的單位圓和位于半徑分別r1、r2之間的具有與正六邊形相同對稱性的閉合曲線。由于在w平面上該系統的內導體的橫截面的形狀為圓，外導體可近似看作半徑為的圓（見圖2），其內部電場在該截面上的分布近似呈軸對稱性，故在w平面上可近似地按同軸帶電圓柱體的情形來討論電場的分布規律。再根據變換關系變換到z平面，最終得到接地圓筒內帶電正六棱柱的電場分布，并根據變換結論計算出該導體系統單位長度的電容量。

2 內帶電正六棱柱-外接地圓筒系統的電場分布

設內正六棱柱-外接地圓筒系統內、外導體之間的電壓為V0，由于保角變換并不能改變內、外兩導體之間的電壓，故變換后的近似同軸圓柱系統（內半徑為1，外半徑近似為）內、外兩導體間的電壓仍為V0。

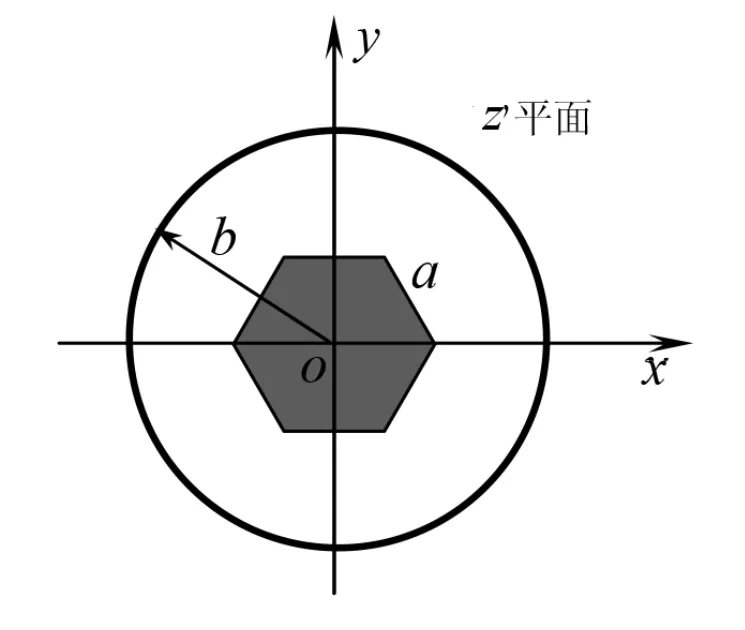
圖1 變換前的內正六棱柱-外圓筒系統的橫截面

對帶電同軸圓柱系統，其中的電場分布是徑向的[2]375-381，大小與半徑成反比。即：

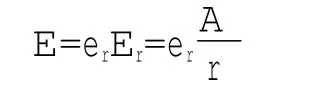
式中er為同軸圓柱系統橫截面上的徑向單位矢，A為與電場幅值有關的常數。而

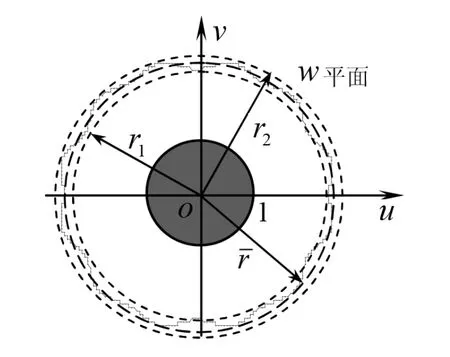
圖2 變換后前的內正六棱柱-外圓筒系統的橫截面

則

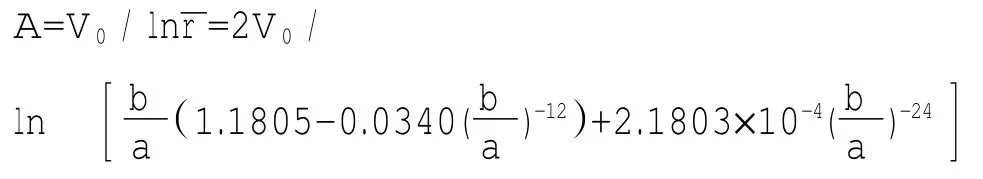
在變換后的w平面上，內正六棱柱-外接地圓筒系統的橫截面映射為同心圓，故內正六棱柱-外接地圓筒系統內的電勢分布為：

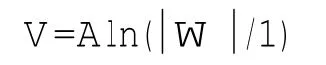
將式(1)代入上式，即得內正六棱柱-外接地圓筒系統內的電勢分布為：

式（5）即為內帶電正六棱柱-外接地圓筒系統內的電勢分布表達式，其中

內帶電正六棱柱-外接地圓筒系統內的場強分布的表達式，可進一步通過電勢與場強的微分關系E=-?φ求得。

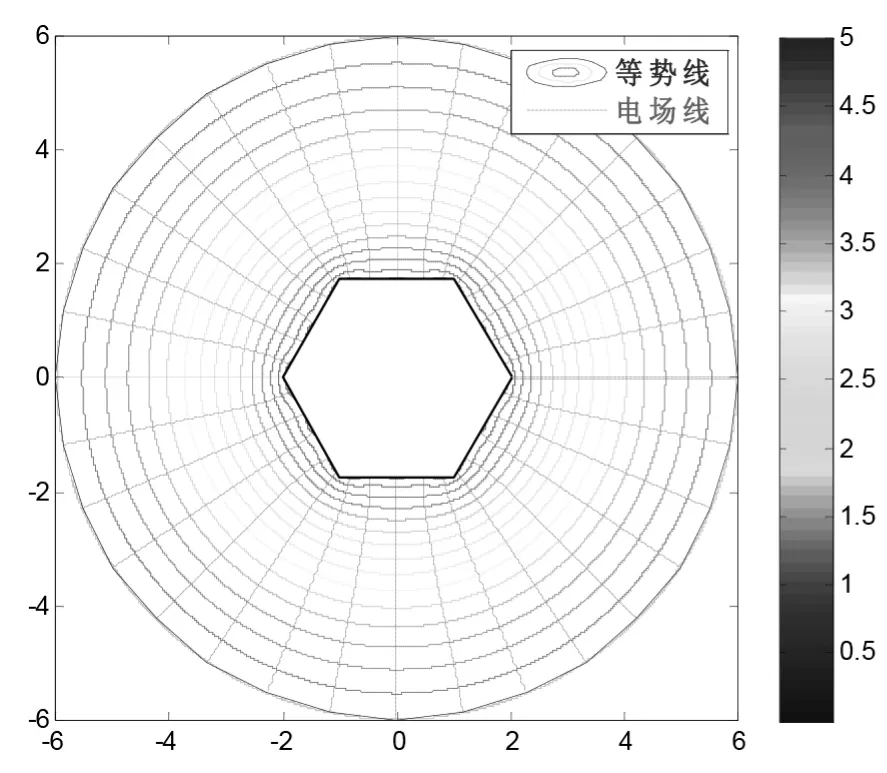
圖3 內帶電正六棱柱-外接地圓筒系統橫截面上的電場線與等勢線（面）圖（a=2cm，b=4cm）

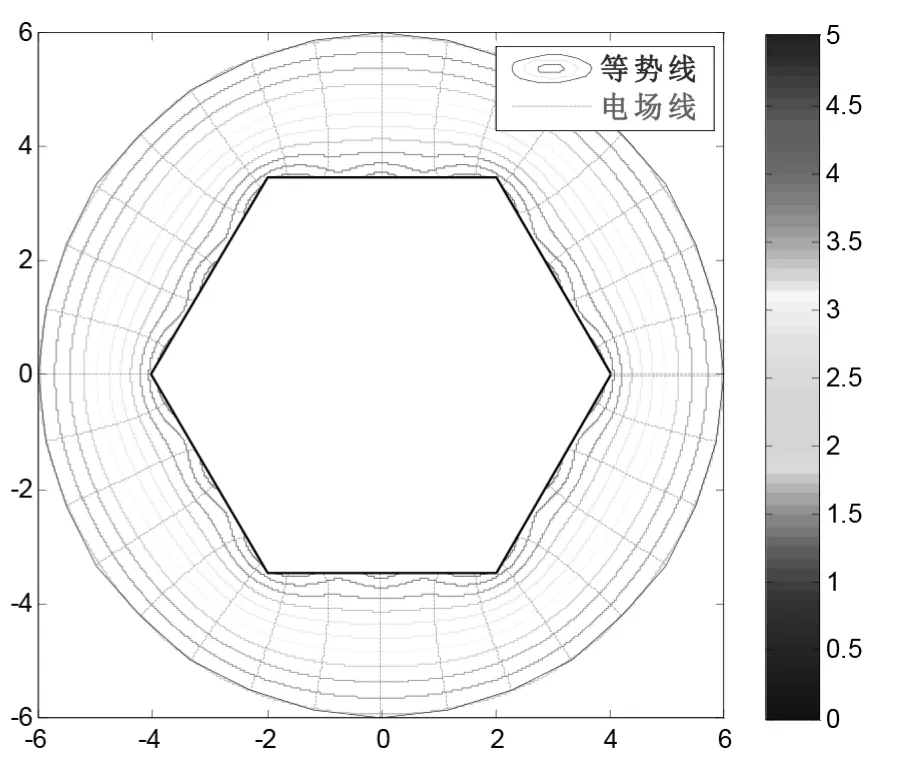
圖4 內帶電正六棱柱-外接地圓筒系統橫截面上的電場線與等勢線（面）圖（a=4cm，b=6cm）

圖3和圖4為利用MATLAB軟件所繪制出的內帶電正六棱柱-外接地圓筒系統的電場線與等勢線（面）圖。從該圖可以看出，電場在帶電系統橫截面上呈對稱分布，作出的圖與預期結果（電場線與等勢線及導體表面均垂直）相符。

3 內正六棱柱-外接地圓筒系統單位長度的電容

經變換式（1）和（4），內正六棱柱-外圓筒的橫截面已映射為半徑分別為1和兩近似同心圓。由于映射前后傳輸線單位長度的電容量保持不變，這樣就可由內、外半徑分別為1和同軸圓柱的電容值，通過公式方便地求出此系統電容的近似值。據此，內正六棱柱-外圓筒單位長度電容的計算公式如下：

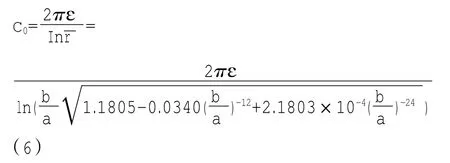
其中ε為內正六棱柱外接地圓筒填充介質的介電常數，當其內部為空氣時，介質的電磁參量取ε0。

需要說明的是，由于電荷的角效應，內導體棱角處電荷密度大，而每邊中點處的電荷密度小。對變換后的圖2而言，內圓柱導體與無電荷角效應的外切圓弧之間的電容，要比其與內切圓弧之間的電容要大。所以，對于用內切圓和外切圓的邊界尺寸取幾何平均來“逼近”變換后的多邊形外導體邊界。由于交替出現了電容增大和電容減小的情況，故對計算總平均電容來說，電荷角效應的影響很小。因此，由式（6）計算出的內正六棱柱外圓筒電容的近似值，具有較高的精確度。表1中分別列出了相應計算方法與多極理論及矩量法所得的結果（介質為空氣）。通過比較可以看出，文章的計算結果與由多極理論的計算結果相當接近，相對誤差的最大值為7‰，最小值為2.7‰，平均相對誤差為3.9‰。表1中的計算結果也與文獻[3-6]給出的數據幾乎一致，相對差值均在2‰以內。由此也可佐證本文所給出的研究方法的正確性，文獻[7]所給出的矩量法的計算結果稍有誤差。

式（6）為內正六棱柱-外圓筒電容量的解析計算式。通過保角變換法計算復雜截面傳輸線的特性阻抗，公式推導過程簡單，物理意義明確，精確度很高，可方便地計算任意尺寸的內正六棱柱-外圓筒的電容量。復雜截面系統的電容量也可用多極理論或矩量法計算，但多極理論準解析計算規則需要針對不同情形確定不同的內極、外極和極的次數等，原理相對復雜。而矩量法需對計算區域進行離散化處理，離散網格尺寸大小是求解精確性的關鍵。一般而言，網格越小越精確，但由于減小網格尺寸勢必造成未知量數目的增加，使得存儲量和計算量大幅增加，因此矩量法計算復雜截面系統電容量的精度受計算機內存的限制，此即文獻[7]所給出的用矩量法計算內正六棱柱-外圓筒電容的數值，與其他方法相比較稍有偏差的原因。

表1 內正六棱柱外接地圓筒的電容量C0(×10-11F)（R為外導體半徑，r為內導體內接圓的半徑,填充介質 ε=ε0、u=u0）

4 結束語

文章采用數值保角變換法對帶電內正六棱柱外接地圓筒進行了研究，給出了該帶電系統內電場的近似解析解，為不屬于同一族正交坐標系的帶電系統的電場分布的研究提供了一種思路和方法。這種方法物理意義明確、計算簡單，所得結論對于研究內正六邊形-外圓傳輸線內TEM波場結構及其特性阻抗的計算，亦具有一定的參考價值和理論意義。

［1］任偉，林為干.特種截面傳輸線的分析［J］.電子科學學刊,1990,12（1）:38-46.

［2］沈熙寧.電磁場與電磁波［M］.北京：科學出版社，2006.375-381.

［3］佘顯燁，方漢平.結合保角變換的優化模擬鏡像法解多種截面形狀同軸傳輸線的特性阻抗［J］.電子科學學刊,1995,17（3）：283-289.

［4］Sheng-gen Pan.CharacteristicImpedance of a CoaxialSystem Consisting of Circular and Noncircular Conductors［J］.IEEE.Trans.Microwave Theory Tech,1988,36(5)：917-921.

［5］徐善駕，等.任意橫截面形狀同軸線的高次有限元分析［J］.電子科學學刊,1992,14（4）:396-403.

［6］Wheeler H A.Transmission-line Conductors of Various Cross Section.IEEE.Trans.Microwave Theory Tech，1980,MTT-28：73-83.

［7］呂文俊，曹偉，朱洪波.具有屏蔽導體的多導體傳輸線的矩量法分析［J］.南京郵電學院學報,2003，23（2）：21-25.

Wang Fu-qian

（Department of Electronic Information and Physics,Changzhi University,Changzhi,Shanxi 046011）

The electric field distribution of a charged regular hexagonal prism in the grounding conductor cylinder is proposed by using numerical conformal mapping,and field pattern on its cross section is plotted,furthermore，its capacitance of per unit length is calculated.

grounding conductor cylinde;a charged regular hexagonal prism;numerical conformal mapping;electric field distribution;capacitance

O457

A

1673-2015（2015）02-0008-04

（責任編輯 郝瑞宇）

山西省自然科學基金（2012011028-1）；山西省高等學校科技研究開發自選項目（20121116）。

2014—10—03

王福謙（1957—）男，山西臨猗人，教授，主要從事電磁場理論及場結構數值模擬研究。