復數域上低次代數中的對合計算

張巧紅，石曉磊

（長治學院 數學系，山西 長治 046000）

復數域上低次代數中的對合計算

張巧紅，石曉磊

（長治學院 數學系，山西 長治 046000）

在矩陣理論中，稱滿足條件A2=E的矩陣為對合矩陣。文章主要類比對合矩陣，討論在復數域上的三次及四次代數中的對合計算，給出復數域上的三次及四次代數中向量方程v2=e的所有可能的解.

群；代數；對合

1 預備知識

定義1[1]191設V是數域P上的線性空間，G是一個群，且G中的元素是V中的一組基.在V上除了定義了加法，數乘運算之外還定義了乘法運算.定義了乘法運算的線性空間V若滿足乘法對加法的分配律，并且對于任意v1，v2∈V及任意k∈P，有：

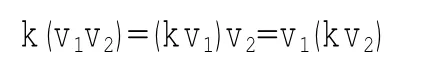
則稱V是一個代數.

注：當G為乘群[2]10時，則稱V為群代數；

代數V的乘群（G，·）如果是半群，則稱V為結合代數；

代數V作為數域P上線性空間的維數，稱為V的次數.

例如：Mn(P)是域P上的所有n階方陣組成的集合，顯然它是P上的一個代數.

2 復數域上三次代數中的對合計算

定理1 設群G=={a，a2，e}，V3={k1a+k2a2+ k3e|k1，k2，k3∈C}，則V3是一個三維線性空間，a，a2，e就是該三維線性空間的一組基，且V3也是一個代數.

證明：任取 V3中的元素 v1，v2,不妨設v1=r1a+r2a2+r3e，v2=s1a+s2a2+s3e,定義v1+v2=(r1a+r2a2+r3e)+(s1a+s2a2+s3e)=(r1+s1)a+(r2+s2)a2+ (r3+s3)e,則加法滿足封閉性；任取 k∈C及 v=k1a+k2a2+k3e∈V3, 定 義 kv=k (k1a+k2a2+k3e) =kk1a+kk2a2+kk3e∈V3，則數量乘法滿足封閉性.易證加法和數乘運算滿足線性空間定義[3]248中的八條運算規則，從而V3對上述定義的加法和數乘運算構成復數域C上的線性空間.

因為V3中任一個元素均可由a，a2，e線性表出，現假設k1a+k2a2+k3e=0，必有k1=k2=k3=0.若否，不妨設k1≠0，k2=k3=0，則有k1a=0，由k1≠0得a=0，矛盾,故a，a2，e是線性空間V3的一組基，其維數為3.

下證V3是復數域C上的三次代數：任取v1，v2∈V3，不妨設v1=r1a+r2a2+r3e，v2=s1a+s2a2+s3e在V3中定義一個乘法運算 v1v2= (r1s3+r3s1+r2s2)a+ (r1s1+r2s3+r3s2)a2+(r1s2+r2s1+r3s3)e,故 v1v2∈V3，且易證乘法對加法滿足分配律.又對于任意的v1,v2∈V及k∈C，可證得k(v1v2)=(kv1)v2=v1(kv2)成立，故V3是復數域C上的三次代數，且為群代數.

注：由于V3關于乘法構成半群，故V3是一結合代數.

下在V3中求v2=e的解.在V3中任取一元素v=r1a+r2a2+r3e，若v2=e，則v2=(2r1r3+r22)a+(2r2r3+r12)a22+ (2r1r2+r32)e=e

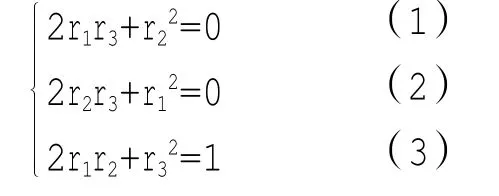
變形得

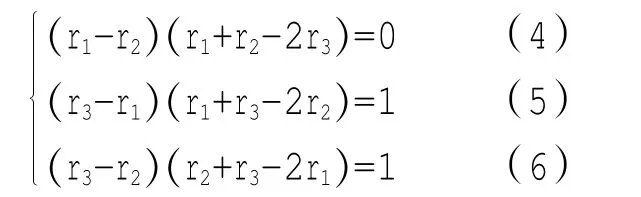
解該方程組可得(r1r2r3)為:

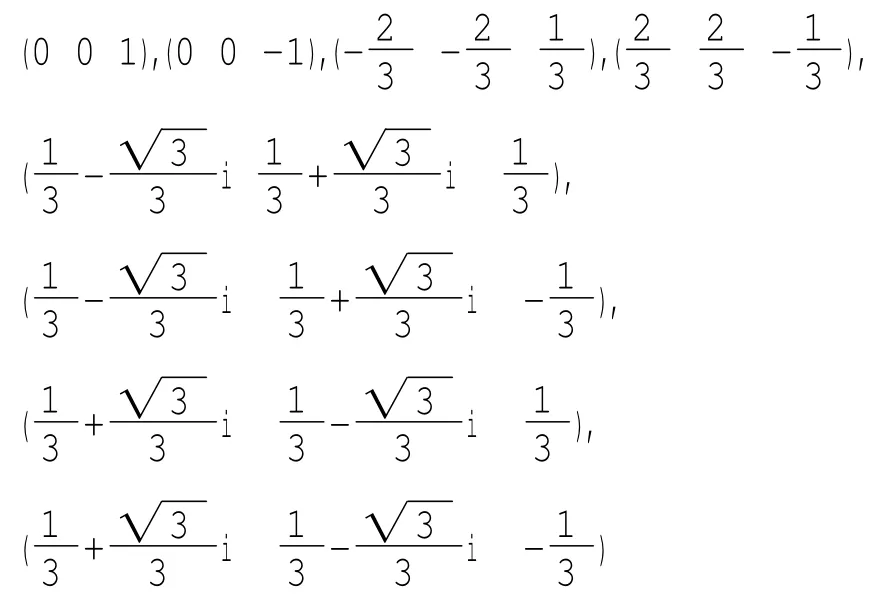
由上可得：復數域上三次代數中方程v2=e的解的個數是23=8.

3 復數域上四次代數中的對合計算

令 群 G== {a，a2，a3，e}， 設 V4= {k1a+k2a2+k3a3+k4e|k1，k2，k3，k4∈C},同上可證V4是一個四維線性空間,a，a2，a3，e是該四維線性空間的基,且V4也是復數域C上的一個代數.

下在V4中求解方程組v2=e.對任意

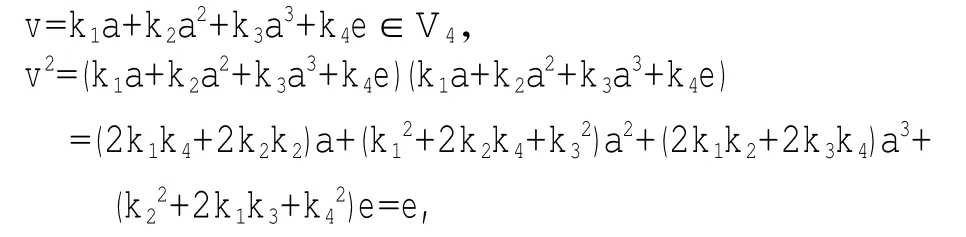
對比系數得：

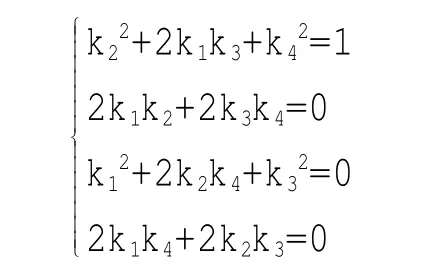
解該方程組可得(k1,k2,k3,k4)為:

由上可得：復數域上四次代數中方程v2=e的解的個數是24=16.

［1］徐明曜.有限群導引［M］.北京:科學出版社,1999.

［2］唐高華.近世代數［M］.北京:清華大學出版社, 2008.

［3］北京大學數學系幾何與代數教研室.高等代數（第三版）［M］.北京:高等教育出版社,2003.

Zhang Qiao-hong Shi Xiao-lei

（Department of Mathematics，changzhi University，changzhi shanxi，046000）

A matrix is called an involution if A2=E.The article deals with the involution calculation in low-dimensional C-algebra,where C is the complex domain.All the solutions of the equation v2=e in low-dimensional C-algebra have been listed here.

Group；algebra；Involution

O15

A

1673-2015（2015）02-0032-02

（責任編輯 趙巨濤）

2014—12—13

張巧紅（1980—）女,山西高平人，碩士，主要從事基礎數學研究。