多表達式程序設計的新型評估方法*
鄭秋生,何 锫,2,3,李 驥
(1.長沙理工大學計算機與通信工程學院,湖南 長沙 410114;2.廣州大學計算機科學與教育軟件學院,廣東 廣州 510006;3.北京大學高可信軟件技術教育部重點實驗室,北京 100871)
1 引言
遺傳程序設計GP(Genetic Programming)[1]是重要的自動程序設計方法,包括線性與非線性表示兩類。多表達式程序設計MEP(Multi Expression Programming)、基因表達式程序設計GEP(Gene Expression Programming)、文法演化GE(Grammatical Evolution)以及Hoare語義型遺傳程序設計等都是線性表達的遺傳程序設計方法[2~9],它們在多目標優(yōu)化、金融預測、海量數(shù)據(jù)分析、軟件工程、信息安全等領域都得到了廣泛的應用[6, 10]。
與傳統(tǒng)GP相比較,MEP等線性表達的GP(某些文獻也將線性表達的GP簡稱為線性GP)既便于個體表示、遺傳操作,又易于描述復雜結構和實現(xiàn),因此自提出以來一直很受關注。然而一切GP都以遺傳算法[11]為基礎,因而轉換、評估工作十分繁復,除要將個體的樹型/線性表示方式轉換成相應的表現(xiàn)型外,還要執(zhí)行、測試所得的近似解以確認它的合適程度。如此一來,評估(某些語義計算甚至一個小小的步驟就得耗費數(shù)十小時以上)等的計算耗費了大量的時空資源,成為GP研究的挑戰(zhàn)性問題[12]。
本文擬就評估問題對MEP做深入探討。先系統(tǒng)化分析它的表示、評估過程中重復計算現(xiàn)象的根源所在,而后給出規(guī)避這些問題的理論依據(jù)、實際解決方案。因無須重復計算相同的語義工作,新方法在演化效率上有了顯著提高。
2 背景和相關工作
多表達式程序設計[3,6,9]作為線性表達的遺傳程序設計方法,主要通過將搜索目標分為基因型與表現(xiàn)型兩個層面來規(guī)范求解過程。由于引入了雙層概念,MEP等線性表達方法的評估須先履行兩型間的轉換,而后執(zhí)行、測試表現(xiàn)型所刻畫的程序。
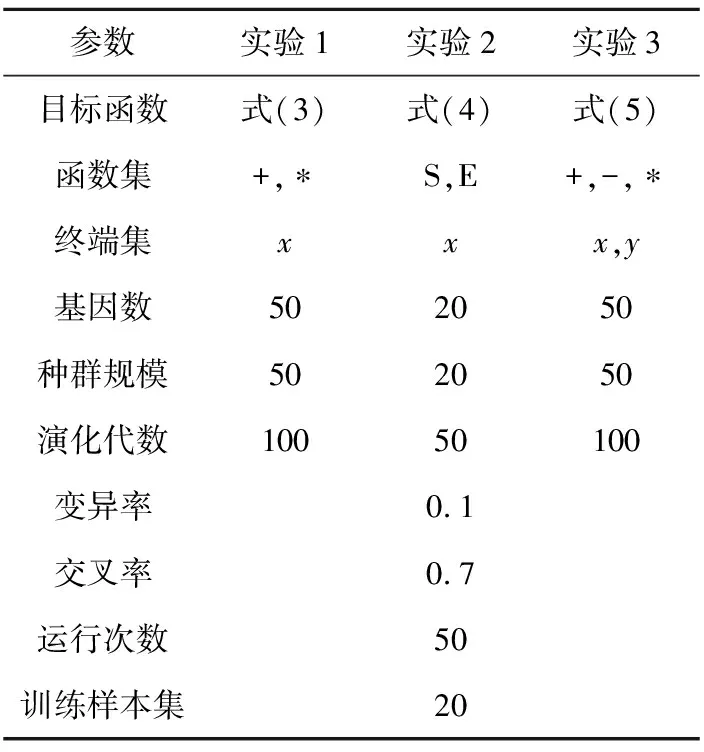
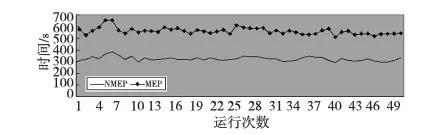
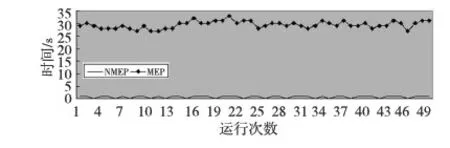
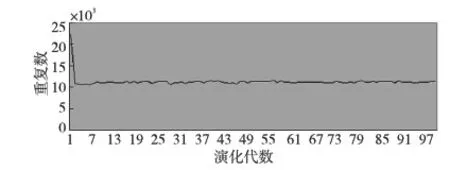
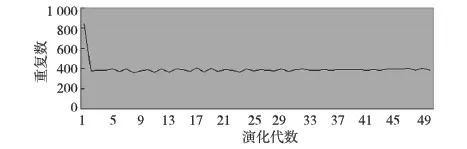
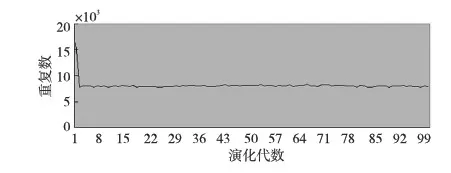
MEP的個體可以表示為線性序列c1,c2,…,cn,其中ci(1≤i≤n)或取自由常量、變量組成的終端集,或取自函數(shù)集F,當然此時須依函數(shù)的數(shù)目以及此前獲得的cj(1≤j Table 1 MEP individual representation 表1中基因1對應的表現(xiàn)型或表達式為a;基因2對應的表達式為b;基因3的表達式為a+b;基因4的表達式為a;基因5的表達式為b×(a+b);基因6的表達式為(b×(a+b))+a。由此可見,語義的重復計算現(xiàn)象會充斥評估過程,這在MEP里尤為明顯。 有關MEP的算法流程如下所示(讀者也可以參見文獻[3,6,9]): (1)隨機產生一個個體種群; (2)評估種群中的個體,若滿足評估標準、精度或算法終止條件,則停止,最佳個體所表征的解即為所求目標; (3)若不滿足終止條件,則在當前種群上實施雜交、變異等遺傳操作以期獲得新的種群; (4)轉第(2)步,反復迭代。 MEP的應用[6,9,13~20]概括地講涵蓋數(shù)字電路設計、天線設計、符號回歸、金融預測與建模、分類、數(shù)據(jù)分析、入侵檢測、決策支持系統(tǒng)、算法設計以及TSP求解等領域。圖像配準是利用圖像序列實施3D重建的關鍵任務。文獻[17]將這一難題歸結為面向特征點的公式發(fā)現(xiàn)問題,嘗試采用MEP求解。 文獻[13]等則探討了MEP等諸多線性表達的GP在基本入侵檢測方面的應用。Alavi A H團隊[18~20]解決實際工程應用問題多次采用了MEP。如他們在文獻[18]中借助MEP對瀝青混合材料的永久變形進行分析;在文獻[19]中對土壤液化的評估實施MEP建模。MEP在國內也得到了關注。文獻[14,15]等充分考慮GEP、MEP的優(yōu)勢,在個體表示、解讀方面做了努力,提高了性能。 綜上所述,MEP應用面很廣,是解決數(shù)據(jù)分析、實際工程應用問題的有力工具。然而,MEP與其他GP家族成員一樣,也有計算量大、評估耗時的不足。鑒于目前直接改進其評估工作的研究尚不多見,以下擬系統(tǒng)深入地分析個體表示,嘗試規(guī)避評估過程凸顯的重復計值現(xiàn)象,從而提高算法性能。 MEP實質是以一定法則不斷改變、演化產生新的個體集(也叫種群)的方式來獲取問題的解的。從第2節(jié)的表1易見,個體的評估會出現(xiàn)大量重復計值現(xiàn)象。本節(jié)將深入分析MEP算法模型上的這一問題,指出重復計值現(xiàn)象產生的充分條件和理論計算依據(jù)。 定理1設MEP的函數(shù)集和終端集分別是F、T,T中終端符的個數(shù)為|T|,則染色體中基因個數(shù)多于|T|時,必有重復運算。 定義1(等型基因) 設I是MEP系統(tǒng)中長度為d的個體(染色體),I中第d1、d2(1≤d1,d2≤d)兩號基因等型,如果它們所表征的表現(xiàn)型或抽象語法樹一致。 定理2設MEP的函數(shù)集和終端集分別是F、T,那么評估個體I的長為d的前綴片段(個體前d個基因構成的基因片段)所需的運算量總數(shù),記為N(T,F,I,d),可由式(1)獲得。 (1) 其中,di是基因在個體I中的下標。 證明施歸納于個體前綴基因片段的長度d如下: (1)歸納基始:d=0或1時,結論顯見成立。 (2)歸納論證步驟分兩步進行。 ①當?shù)赿個基因為終端符時: 評估d個前綴基因的總運算量N(T,F,I,d)實質是在前d-1個基因評估運算量基礎上增加了一次常量提取運算,因而結論成立,符合公式描述。 ②當?shù)赿個基因為函數(shù)運算f(d1,d2,…,dm)時:d個前綴基因的總評估運算量N(T,F,I,d)應包括前d-1個基因的評估運算量與f(d1,d2,…,dm)本身的運算量兩部分。據(jù)歸納假設,前者是N(T,F,I,d-1),后者宜為第d1,d2,…,dm個基因的評估運算量加上一次m元運算f(d1,d2,…,dm)。又對任意i(1≤i≤m),第di個基因本身的評估運算量可借助歸納假設和總運算量概念表達為:N(T,F,I,d)-N(T,F,I,di-1)。故此結論成立。 □ 為方便理解,表1同時給出了染色體前綴運算總量的計值示例。由定義1易見,基因間的等型關系是一種等價關系。下面的定理3將著力回答評估中的重復運算問題。 證明需注意三點: (1)等型基因類中的元素僅需實際計算一個(比如該類中被第一個分析和發(fā)現(xiàn)的元素)。 (2)實際計算等型基因類中的一個元素時,涉及F∪T上符號所表征的計值運算僅有一次。因為參與復合運算的子樹是低深度的子樹,其計值早在低深度基因類分析過程中已完成,可以直接引用(不涉及F∪T中元素所明確表示的運算)。 (3)關于深度為1的等型類的計值問題,這里按計值一次的方式處理(涉及到T中符號,有可能存在某些轉換),其它重復現(xiàn)象可以通過引用獲得(不必做有關轉換)。 至此,我們分析了MEP的重復計值問題。它們包括個體內與種群中個體間的重復計值現(xiàn)象,其中后者較為隱蔽。下節(jié)將據(jù)定理3等結論給出去除重復計算現(xiàn)象的具體技術方案。實際應用過程中,定理3可以施用于演化過程產生的所有種群和個體,這只需將定理中的d視為演化過程中所有個體首尾銜接形成的大個體即可。 依據(jù)以上定理,本節(jié)介紹具有去除重復運算功能的評估方案:處理單個基因的算法NMEP及嵌入NMEP的MEP演化算法。 算法NMEP基本思想:通過不斷構建等型基因有向圖Q(V,E)來識別重復的基因,從而避免重復計算。V是頂點集,E是有向邊集,V中每個頂點有編號且對應一個基因,并存儲該基因的信息。 算法NMEP 輸入:基因g。 輸出:基因g在V中的相關頂點編號及g的其他信息。 步驟1本步驟只在MEP初始化種群之前執(zhí)行一次。初始化等型基因有向圖Q(V,E):終端符集T={z1,…,zk}中每個終端符代表的基因g1,…,gk均屬不同等型基因類,故在V中創(chuàng)建它們對應的頂點v1,…,vk(下標1,2,…,k是頂點在V中的編號,下同),并對所有頂點從1開始依序編號。將基因g1,…,gk所涵蓋的語義動作及其基因信息分別寫入v1,…,vk頂點中。num_gene等于V中頂點數(shù)。 步驟2演化過程中,如果基因g取自T中終端符,由于步驟1已對T中所有終端符進行處理,則直接找到V中與基因g同屬一個等型基因類的基因g′對應的頂點v′,輸出v′的編號及其基因信息。 步驟3如果基因g是函數(shù)形式(pg,s1,…,sn),其中pg是操作符,s1,…,sn是它的參數(shù),s1,…,sn所對應的基因gs1,…,gsn必然已被處理,找到基因gs1,…,gsn在V中對應的頂點編號a1,…,an。對算法中的操作符需要考慮交換率時,執(zhí)行步驟3.1、步驟3.3和步驟3.4;不需要時,執(zhí)行步驟3.2、步驟3.3和步驟3.4。 步驟3.1當算法適用交換率時,如果pg滿足交換率,則需要將a1,…,an按一定順序排列成標準序列(本算法以a1,…,an的升序排列結果作為標準序列t1,…,tn),如此便于在步驟3.4的操作中查找滿足與基因g重復條件的基因;否則,如果pg不滿足交換率,把a1,…,an賦值給t1,…tn;最后,找到頂點vt1。 步驟3.2當算法不適用交換率時,把a1,…,an賦值給t1,…,tn;最后,找到頂點vt1。 為此,嵌入NMEP進行評估去重的算法可重新表述如下: Begin: 初始化種群; for(i=1;i≤演化代數(shù);i++) {for(j=1;j≤種群大小;j++) {依次處理種群的每個個體q:用算法NMEP處理個體中的每個基因;} 如果(i<演化代數(shù)) {交叉;變異;} } 輸出最佳個體; End 由以上敘述可知,NMEP僅在評估時對MEP的基因進行了等價去重處理,并沒有對演化規(guī)則、過程進行任何變動,因而嵌入NMEP的MEP與傳統(tǒng)MEP應有一樣的精度,自然無需就精度進行實驗比較。 新方法采用MEP的適應值計算方法,即計算單染色體中所有基因的適應值,然后以最佳值來表征個體適應值,詳見式(2)。 (2) 本節(jié)針對符號回歸問題做了三個實驗,其中目標函數(shù)如式(3)~式(5)所示,x,y∈[-100,100],涉及的參數(shù)見表2,S和E分別表示sin和exp運算,比較的對象是運行時間。 z=x4+x3+x2+x (3) z=sin(exp(sin(exp(sin(x))))) (4) z=x3+x2y-y (5) 為更好地體現(xiàn)新方法的時間優(yōu)勢(主要得益于消除基因的重復引用,即語義的重復計算現(xiàn)象),還增加了演化過程的語義復雜度,如為每個基因的處理/運行額外添加了語義延時程序extra()。它的一次執(zhí)行將達萬次“a++”之眾。 Table 2 Parameters of experiment 1~experiment 3 圖2~圖4為通過實驗1~實驗3對比嵌入NMEP的MEP與傳統(tǒng)MEP的時間開銷,圖中橫坐標表示運行次數(shù),縱坐標表示時間,單位是s。每個實驗都有兩條曲線,位于下方的曲線(時間少)均是嵌入NMEP的MEP的演化時間;位于上方的曲線(時間多)均是傳統(tǒng)MEP的演化時間。由圖2~圖4可知,傳統(tǒng)MEP在時間性能上明顯落后于嵌入NMEP的MEP,也即新評估方法擁有較大的時間優(yōu)勢。 Figure 2 Time comparison between NMEP-based MEP and traditional MEP in experiment 1圖2 實驗1中嵌入NMEP的MEP與傳統(tǒng)MEP時間比較 Figure 3 Time comparison between NMEP-based MEP and traditional MEP in experiment 2圖3 實驗2中嵌入NMEP的MEP與傳統(tǒng)MEP時間比較 Figure 4 Time comparison between NMEP-based MEP and traditional MEP in experiment 3圖5 實驗3中嵌入NMEP的MEP與傳統(tǒng)MEP時間比較 圖5~圖7刻畫三個實驗中NMEP查出傳統(tǒng)MEP演化過程包含的基因的重復次數(shù)。圖中橫坐標表示演化代數(shù),縱坐標表示傳統(tǒng)MEP的基因的重復引用次數(shù)。從圖5~圖7的基因的重復引用總量看來,重復量是不可小覷的。試想如果被重復計算的語義動作的時間復雜度很高,那么大量重復將耗費龐大的運算時間和其他資源。 Figure 5 Repeat number NMEP finds out in experiment 1圖5 實驗1中算法NMEP查找出的重復次數(shù) Figure 6 Repeat number NMEP finds out in experiment 2圖6 實驗2中算法NMEP查找出的重復次數(shù) Figure 7 Repeat number NMEP finds out in experiment 3圖7 實驗3中算法NMEP查找出的重復次數(shù) 綜觀圖2~圖7,當傳統(tǒng)MEP的種群在演化過程中涉及的基因重復引用量、語義動作的運算量越大,嵌入NMEP的MEP所節(jié)省的時間就越多。由上可知,嵌入NMEP的MEP在不改變傳統(tǒng)MEP演化規(guī)則和精度的基礎上,能夠準確有效地識別被重復使用的基因,避免重復計算帶來的大量的資源消耗,使得MEP在性能上得到較大的提高。這表明,針對MEP的去重運算研究不僅具有充分的理論依據(jù),而且在具體實現(xiàn)環(huán)節(jié)也是可行的,是擁有重要前景的一個研究領域。 本文首先深入分析了MEP的基因在染色體中的表示特點及采用的評估方法,發(fā)現(xiàn)每個染色體中的任何基因都有可能多次被當前或其它后續(xù)種群中的其他基因引用,造成重復計算的現(xiàn)象,繼而給出了現(xiàn)象出現(xiàn)的充分條件,以及處理的理論依據(jù)和具體算法。算法NMEP在保證與傳統(tǒng)MEP精度相同的基礎上,能有效識別會被重復引用的基因,避免大量重復計算,節(jié)省了寶貴的時空資源。最后的實驗結論表明,去重計值后,嵌入NMEP的MEP在性能上有顯著提高。可見,去重研究對于MEP的整體研究具有重要的意義。我們下一步將用類似方法分析GEP的評估問題,相信在深度優(yōu)先解碼方式下會有相似效果。 [1] Koza J R.Genetic programming:On the programming of computers by means of natural selection[M]. Cambridge:MIT Press, 1992. [2] Ferreira C.Gene expression programming:A new adaptive algorithm for solving problems[J]. Complex Systems, 2001, 13(2):87-92. [3] Oltean M, Grosan C. A comparison of several linear genetic programming techniques[J]. Complex Systems, 2003, 14(4):285-313. [4] McKay R I, Hoal N X, Whigham P A,et al. Grammar-based genetic programming:A survey[J]. Genetic Programming and Evolvable Machines, 2010, 11(3-4):365-396. [5] O′Neill M, Ryan C. Grammatical evolution[M]. Dordrecht:Kluwer Academic Publishers, 2013. [6] Oltean M, Grosan C, Diosan L,et al. Genetic programming with linear representation:A survey[J]. International Journal on Artificial Intelligence Tools, 2009, 19(2):197-239. [7] He Pei,Kang Li-shan,Johnson C G,et al.Hoare logic-based genetic programming[J]. Science China(Information Sciences), 2011, 54(3):623-637. [8] He Pei, Johnson C G, Wang Hou-feng. Modeling grammatical evolution by automation[J]. Science China Information Sciences, 2011, 54(12):2544-2553. [9] Oltean M. Improving the search by encoding multiple solutions in a chromosome[M]∥Evolutionary Machine Design:Methodology and Applications,2005:88-110. [10] Harman M. Software engineering meets evolutionary computation[J]. IEEE Computer, 2011, 44(10):31-39. [11] Mitchell M. An introduction to genetic algorithms[J].Cambridge:MIT Press, 1996. [12] O’Neill M, Vanneschi L, Gustafson S,et al. Open issues in genetic programming[J].Genetic Programming and Evolvable Machine, 2010, 11(3):339-363. [13] Wu Shelly Xiaonan, Banzhaf W. The use of computational intelligence in intrusion detection systems:A review[J].Applied Soft Computing, 2010(10):1-35. [14] Dai Mu-cheng,Tang Chang-jie,Zhu Ming-fang,et al.Automatic complex function discovery based on multi expression gene programming[J]. Journal of Sichuan University(Engineering Science Edition),2008,40(6):121-126.(in Chinese) [15] Deng Wei,He Pei,Qian Jun-yan.Multi-gene expression programming with depth-first decoding principle[J].Pattern Recognition and Artificial Intelligence,2013,26(9):819-828.(in Chinese) [16] Zhang Jia-wei,Wu Zhi-jian,Huang Zhang-can,et al.Classification based on multi expression programming[J]. Journal of Chinese Computer Systems,2010,31(7):1371-1374.(in Chinese) [17] Zhao Xiu-yang, Zhang Cai-ming, Wang Ya-nan,et al. A hybrid approach based on MEP and CSP for contour registration[J].Applied Soft Computing, 2011(11):5391-5399. [18] Mirzahosseini M R, Aghaeifar A, Alavi A H, et al. Permanent deformation analysis of asphalt mixtures using soft computing techniques[J]. Expert Systems with Applications, 2011, 38:6081-6100. [19] Alavi A H, Gandomi A H. Energy-based numerical models for assessment of soil liquefaction[J].Geoscience Frontiers, 2012, 3(4):541-555. [20] Alavi A H, Aminian P, Gandomi A H,et al. Genetic-based modeling of uplift capacity of suction caissons[J].Expert Systems with Applications, 2011, 38:12608-12618. [21] Jiang Da-zhi,Peng Chen-feng,Liu Liang. Forecasting soil slope stability with MEP algorithm[J]. Journal of Shantou University(Natural Science Edition),2011,26(4):66-72.(in Chinese) 附中文參考文獻: [14] 代術成,唐常杰,朱明放,等.基于多表達式基因編程的復雜函數(shù)挖掘算法[J].四川大學學報(工程科學版),2008,40(6):121-126. [15] 鄧薇, 何锫, 錢俊彥. 深度優(yōu)先的多基因表達式程序設計[J].模式識別與人工智能,2013,26(9):819-828. [16] 張建偉,吳志健,黃樟燦,等.基于多表達式編程的分類算法研究[J].小型微型計算機系統(tǒng),2010,31(7):1371-1374. [21] 姜大志,彭晨楓,劉亮. 邊坡穩(wěn)定性的預報MEP分類預測算法[J].汕頭大學學報(自然科學版),2011,26(4):66-72.
3 MEP中的重復評估問題
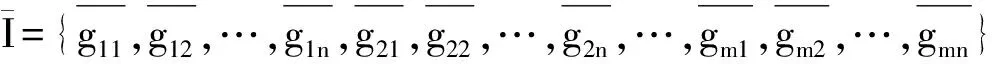
4 新型MEP算法及評估
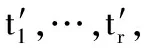
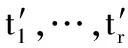
5 實驗分析
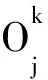
6 結束語

