基于四叉樹分解與圖割的彩色圖像快速分割*

胡志立，郭 敏

(1.現代教育技術教育部重點實驗室，陜西 西安 710062;2.陜西師范大學計算機科學學院，陜西 西安 710062)

1 引言

圖像分割將圖像劃分為有意義的若干區域或者用于提取人們感興趣的區域，它在計算機視覺、模式識別和圖像工程等學科中都發揮著重要的作用。圖割作為一種基于圖論的組合優化方法，可以用來最小化計算機視覺中的能量函數問題。Greig D等[1]首次將圖割應用于圖像處理領域，同時他們最早提出使用功能強大的最小割/最大流算法來最小化計算機視覺中的能量函數；隨著Boykov Y等[2,3]將其應用到圖像分割領域，引發了國際上對圖割理論及其應用的研究熱潮。Boykov Y等[4]提出了基于增廣路徑的新方法：擴展移動(Expansion-moves)和交換移動(Swap-moves)，有效地提高了最小割/最大流算法的效率。Li Y等[5]首先利用分水嶺(Watershed)算法對圖像進行預分割，將圖像分成很多內部顏色較為一致的小區域；然后將每個小區域作為一個節點，利用圖割方法進行劃分，得到最終分割的圖像；利用小區域代替區域內部像素點構造出來的圖的節點明顯減少，然而由于預分割本身的時間較長，所以對圖割時間上的改進較少。Blake A等[6]使用高斯混合模型GMM(Gaussian Mixture Model)對前景和背景顏色空間進行建模，從而能夠較好地利用圖像的顏色信息對彩色圖像進行分割。Rother C等[7]提出的GrabCut采用多次迭代圖割進行圖像分割，它只需要用戶指定一個圍繞目標的矩形框便可提取感興趣的目標，有效減少了用戶交互量。

利用GrabCut多次迭代圖割進行圖像分割，在處理海量級圖像數據時，耗時往往比較大。其切割實質是迭代使用圖割進行高斯混和模型GMM參數估計，直到滿足收斂條件，從而完成圖像分割。整個過程中確定GMM參數成本高，這制約了整個算法的時效性。徐秋平等[8]引入多尺度分析方法，以塔式分解的多尺度圖像序列代替原始圖像進行GMM參數迭代估計，以較少樣本快速確定GMM參數，分割精度不減而效率顯著提高。徐秋平等[9]使用分水嶺變換對圖像進行預處理，以部分具有典型代表的樣本點來估計GMM參數，這有效地提高了GrabCut算法的效率。韓守東等[10]利用多尺度非線性張量紋理特性(MSNST)描述圖像的紋理特征并構建基于MSNST的GMM，使得MSNST能有效地與GrabCut結合；他們還提出一種自適應融合策略來調整混合因子，以有效地融合圖像的色彩特征和MSNST紋理特征，從而得到比GrabCut更好的分割效果。韓守東等[11]在MSNST空間利用獨立尺度分量形式黎曼協方差高斯混合模型(ICRGMM)在紋理聚類中的優勢取代GMM，為了更精確地估計和更新統計參數，使用分量形式期望最大化代替GrabCut原有的K-means算法，使得算法能有效地分割紋理圖像而且對自然場景圖像也有不錯的分割效果；韓守東等[12]使用高斯超像素來構建圖割模型以實現加速，他們使用快速均值漂移算法對圖像進行預分割，從而構建精簡的加權圖。為了準確而精煉地對先驗知識進行參數化學習，他們還使用了分量形式的期望最大化混合高斯算法對用戶交互進行聚類，使得算法在精確性方面和高效性方面都有較好的性能。

基于合并區域然后將整個區域看作一個超像素進行GMM參數估計以減小問題規模的思想，本文使用四叉樹分解來得到區域內顏色相近的圖像塊，我們將整個區域塊描述成超像素，每個超像素點對應著網絡圖的節點，相鄰像素間的差異對應著邊上的容量，以此構建精簡的網絡圖，并用塊內的RGB均值代替該塊內的所有像素點的值進行高斯混合模型參數估計，從而減小問題規模，達到提高GrabCut算法時效的目的。

2 相關研究

2.1 四叉樹分解

四叉樹分解的目標是將原始圖像逐步分成小塊，操作的原理是將具有一致性(像素間的灰度差值小于給定的閾值)的像素分到同一小塊中。四叉樹分解過程如下：令R表示當前進行分解的圖像區域，并選擇一個屬性Q(區域的像素間滿足一致性標準)。如果有Q(R)=FALSE，則將該圖像區域分割為四個象限區域。對于其中的任意一個區域，如果仍有Q(R)=FALSE，則將該象限區域再次細分為四個象限區域，以此類推，直到圖像中的所有區域都滿足一致性標準才停止。最后，四叉樹分解的結果可能包括多種不同尺寸的方塊。由此原理可知，當圖像是正方形，且像素點的行數和列數是2的整數次冪時，四叉樹分解算法是最適用的。對于其它圖形可以通過適當填充來獲得合適的圖像。

2.2 圖割簡介

圖割是一種基于圖論的組合優化方法，它將一幅圖像映射成一個網絡圖，并建立關于標號的能量函數；然后運用最大流/最小割算法對網絡圖進行切割，得到網絡圖的最小割，即能量函數的最小值。設G=(V,E)為一個帶有非負邊權的有向圖，其中V為頂點集，對應圖像的像素點集P，E為邊集。V包含兩個特殊的頂點，通常一個稱為源S，一個稱為匯T。每個頂點有兩個邊，連接源和匯的邊稱為t-links，反映當前頂點對于標記的偏好程度；鄰域連接n-links反映了頂點之間的差異性。最小割就是圖G所有割中容量最小的割，它可根據Ford L和Fulkerson D[13]提出的網絡流理論，通過求網絡圖的最大流而得到。

2.3 GrabCut算法

GrabCut將圖像表示為矢量Z={z1,z2,…,zn,…,zN}，將該圖像的分割表示為求每個像素點的值α={α1,α2,…,αn,…,αN}，αn∈{0,1}，其中0表示背景，1表示前景。GrabCut使用兩個GMM，一個對應背景，另一個對應前景。每個GMM由K個高斯模型混合而成(通常K=5)，每個像素有一個參數kn(kn∈{1,…,K})，參數來自前景還是背景取決于αn的取值。GrabCut算法的Gibbs能量函數形式為[7]：

E(α,k,θ,z)=U(α,k,θ,z)+V(α,z)

(1)

其中，θ代表圖像的GMM參數。

數據項U定義為：

(2)

其中：

D(αn,kn,θ,zn)=

-logp(zn|αn,kn,θ)-logπ(αn,kn)

(3)

其中，p(·)為高斯概率分布；π(·)為混合權重系數，也就是kn為某一個值的像素數占總的像素數的比例。

于是有：

D(αn,kn,θ,zn)=-logπ(αn,kn)+

0.5log det∑(αn,kn)+0.5[zn-

μ(αn,kn)]T∑(αn,kn)-1[zn-μ(αn,kn)]

(4)

那么，參數θ可表示為：

θ={π(α,k),μ(α,k),

∑(α,k),α=0,1,k=1,…,K}

(5)

平滑項V可用RGB空間的歐幾里德距離求得：

(6)

GrabCut算法的主要流程如下：

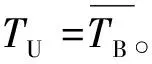
整個GMM參數的迭代估計是在TU中進行的，根據標定的背景區域和未知區域初始化GMM，以下述(1)～(3)對TU迭代直至收斂：

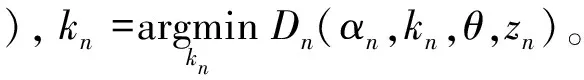
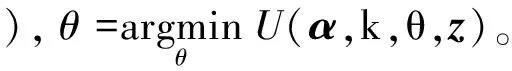
如果當前得到的能量值記為E(i)，上次迭代輸出的能量值為E(i-1)，那么可以將能量變化率定義為：Rate=(E(i-1)-E(i))/E(i-1)，可以將能量變化率是否小于給定的閾值作為判斷GMM參數估計是否收斂的條件。算法收斂后，TF=TU,這樣就分隔出所需的前景部分。

3 基于四叉樹分解和GrabCut的彩色圖像分割方法

3.1 GrabCut算法改進分析

從GrabCut算法的流程可知，其N次迭代收斂過程可分為兩部分：前N-1次迭代使用最大流進行分割，目的是學習、修正GMM參數，第N次分割實現最終的圖像分割。既然前N-1次分割是為了確定GMM參數，而每次使用最大流去最小化能量函數的時間開銷往往比較大，那么使用超像素的方法合并相似的區域，然后再對該塊狀圖構造網絡圖并求解該網絡圖的最大流/最小割，這樣就可以有效減少確定GMM參數的時間消耗。最后，為了使得分割結果盡可能地接近原始算法的精度，我們使用最終得到的GMM參數對原始圖像的TU部分進行分割，從而得到最終結果。

對于一幅2N×2N(如果圖像不是2N×2N，可以適當地進行填充)的圖像，給定閾值進行四叉樹分解，能夠快速地找到圖像中滿足一致性標準的正方形區域。對于灰度圖像，灰度變化值小于給定閾值的像素將會被合并到同一個區域；對于彩色圖像，在RGB分量上變化的均值小于給定閾值的像素會被合并到同一個區域。閾值設置得越高，就會有越多的像素被劃分到同一分塊中，從而分割速度越快，然而過高的閾值使得圖像細節喪失過多，使得最終出現過分割。

綜上所述，本文提出的改進思路是：設置適當的閾值進行四叉樹分解，得到區域內相似度比較高且拓撲結構相對規則的塊狀圖，進而使用各個塊中的RGB均值作為該塊的超像素值，然后再進行GMM參數估計，最后為保證精度，我們使用得到的GMM參數對原始的圖像進行分割，從而達到提高分割速度而精度不減的目的。對于默認的閾值，如果分割結果跟原算法相比存在明顯的過分割，可以降低閾值，直到達到原算法的精度。一般情況下，待提取目標的邊界兩側在顏色上會有一定程度的差異，只要設置好適當的閾值，本文的算法便是可行的。

3.2 塊狀圖的生成

由于四叉樹分解總是將滿足一致性的區域分解成大小相同的四個正方形區域，所以首先要將不是2N×2N的圖像填充成使N盡可能小的2N×2N的圖像再將其轉換成灰度圖像，然后進行四叉樹分解，最后分別將此分解應用到彩色圖像的RGB分量上。考慮到直接對填充后的圖像進行處理，填充的區域會擁有較多的塊數(如將一幅513×513的圖像填充成1 024×1 024)，這樣會增加額外的處理時間，我們將分解后的圖像裁剪成原始大小，然后對裁剪后的圖像建立每塊的索引，并將方形區域內每個像素的RGB值用該區域的RGB均值代替。將分塊圖中的每個分塊看作一個超像素，整個超像素圖可記作B={b1,b2,…,bn,…,bN}，N為節點個數。對于一幅牡丹圖像的處理效果如圖1所示(由圖1b可以看出，四叉樹分解算法可以在一定程度上保持原有的邊界信息和顏色信息，對原有邊界信息和顏色信息保持得越好，最終的分割結果就越接近GrabCut算法的精度)。

Figure 1 Comparison of quadtree decomposition result and orignal image圖1 四叉樹分解預處理結果與原始圖像對比圖

3.3 GMM參數迭代估計

3.3.1 初始化GMM參數

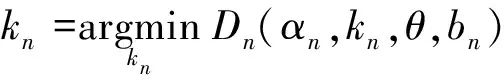
3.3.2 最小割進行分割

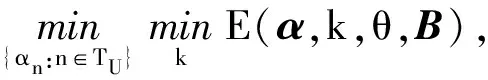
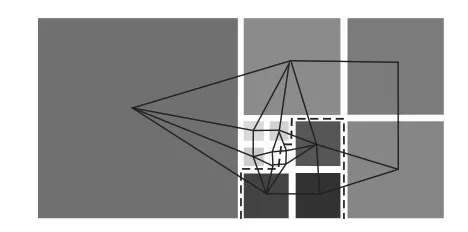
Figure 2 Network graph and minmum cuts圖2 網絡圖與最小割

Figure 3 Results of the first cut圖3 第一次分割的結果

3.3.3 更新GMM參數、判斷收斂及后續處理

每一次最小割分割之后都會將TU中的節點分割成前景或者背景并輸出當前的能量值，將TU中的前景節點作為樣本估計前景GMM參數，TU中的背景節點及TB作為樣本估計背景GMM參數。按照初始化GMM參數的方法計算kn、μ(α,k)、∑(α,k)、π(α,k)，并以此更新GMM參數。判斷收斂的方法與GrabCut一致。程序收斂以后分割的結果鋸齒現象十分明顯，為了保證處理的結果更接近GrabCut算法，我們用得到的GMM參數對原始像素圖的TU部分進行一次分割得到最終結果。

3.4 算法的實現步驟

綜上所述，基于四叉樹與GrabCut的彩色圖像快速分割主要實現步驟如下：

(1)輸入彩色圖像I，將其填充成使得N盡可能小的2N×2N的圖像，再將其轉換成灰度圖像，然后進行四叉樹分解，再將分解后的圖像裁剪成原始大小，然后根據此分解，生成塊狀圖，并建立關于每塊的索引。

(2)根據塊索引，初始化分塊圖的GMM：

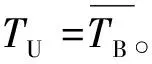
②對于bn∈TB，有αn=0；bn∈TU，有αn=1；其中αn=0代表背景，αn=1代表前景，并以此初始化GMM。

(3)迭代估計GMM參數：

①初始化GMM參數。

②學習GMM參數。

③對超像素圖構造網絡圖，并用最小割進行分割。

④迭代①～③直至滿足收斂條件。

(4)根據所得到的GMM參數對原始圖像I構造S-T網絡，并用最小割算法進行分割。

(5)輸出分割的結果。

4 實驗結果與分析

本文實驗平臺為：64位Windows 7,Matlab R2011a,Microsoft Visual Studio 2010,CPU:Core i5-2450M,RAM:8 GB。對于每一幅圖像，人工設置一個矩形框選中目標區域，然后輸出GrabCut算法、基于分水嶺變換改進的GrabCut算法[8]和本文算法所提取到的目標、二值的分割結果及三者的時間消耗對比圖。無論是使用分水嶺算法預處理得到分塊圖還是使用本文算法預處理得到分塊圖，都因問題規模的減小導致有時改進的算法會比GrabCut算法早收斂，為了方便得到三者的時間消耗對比圖，我們使用規定最大迭代次數這種方法進行處理，只要GrabCut算法已經收斂,就不會對實驗結果造成較大的影響。對于圖1中的原始圖片分割的效果如圖4所示。

Figure 4 Comparison of segmentation of three algorithms圖4 三種算法分割效果對比圖

由實驗結果可看出，本文算法的精度與GrabCut基本一致，但時間上要優于GrabCut。本文算法的時間消耗是1.295 s，GrabCut算法耗時8.814 s，本文算法的時間消耗僅占GrabCut算法的14.69%，通常情況下，基于分水嶺變換改進的GrabCut算法與本文算法在時間上的改進大致相當，且能達到GrabCut算法的精度。

本文算法在運用于圖像分辨率比較高且細節較少的情況下效果更好，圖5和圖6是對一組圖像測試的結果(其中企鵝圖像(680×509)、獵人圖像(680×500)、鯨圖像(1 024×720))。表1是對伯克利圖像分割測試圖庫的另一組圖片測試的結果。

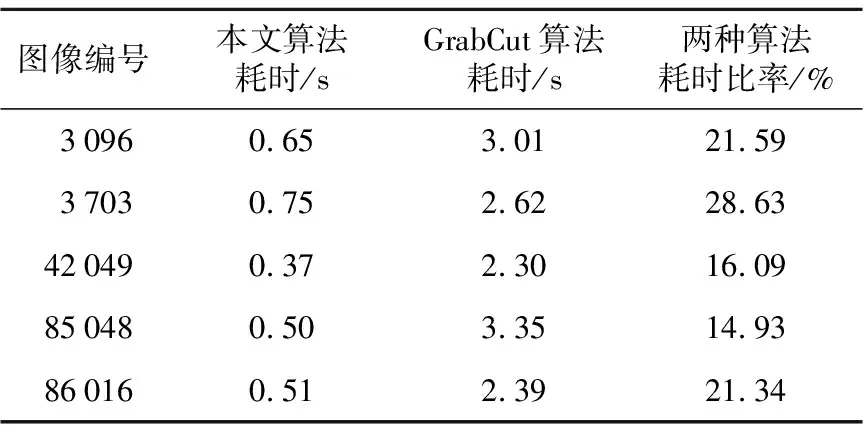
Table 1 Time comparison between our algorithm and GrabCut

Figure 5 Segmentation resutls of three algorithms圖5 三種算法分割效果圖

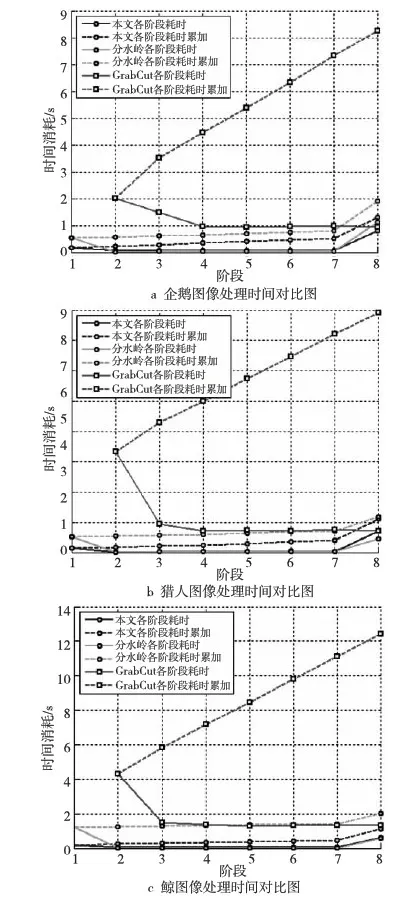
Figure 6 Time comparison among three algorithms圖6 三種算法分割時間對比圖

從上面的圖和表可以看出，本文算法的分割效果與GrabCut非常接近，有的圖像人眼很難分辨兩種算法分割結果的優劣，而時間上明顯優于GrabCut。基于分水嶺變換改進的GrabCut算法與本文算法一樣，都明顯提高了算法的時效性，而且精度上與GrabCut算法十分接近。

5 結束語

GrabCut是一種優秀的交互式圖像分割算法，其用戶交互量少且分割精度高，然而它為了達到一定分割精度而采用多次迭代圖割的方式求解GMM參數，這使得處理海量級圖像數據時，時效性很低。針對該問題，本文使用了合并相似區域然后將整個區域看作一個超像素進行GMM參數估計以減小問題規模的思想，并用四叉樹分解予以實現。實驗結果表明，改進的方法在加快GMM參數估計的同時，基本上保持了和原算法相當的分割效果，這表明了該思想的可行性及有效性。此外，合并相似區域然后將整個區域看作一個超像素進行處理的改進思想也可以推廣到基于圖割理論進行圖像分割、圖像鑲嵌、圖像拼接等其他算法中。

[1] Greig D, Porteous B, Seheult A. Exact maximum a posteriori estimation for binary images[J]. Journal of the Royal Statistical Society(Series B), 1989, 51(2):271-279.

[2] Boykov Y,Jolly M P.Interactive organ segmentation using graph cuts[C]∥Proc of the 3rd International Conference on Medical Image Computing and Computer-Assisted Intervention, 2000:276-286.

[3] Boykov Y,Jolly M P.Interactive graph cuts for optimal boundary and region segmentation of objects in N-D images[C]∥Proc of the 8th IEEE International Conference on Computer Vision, 2001:105-112.

[4] Boykov Y,Veksler O,Zabih R.Fast approximate energy minimization via graph cuts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(11):1222-1239.

[5] Li Y, Sun J, Tang C K, et al. Lazy snapping[J]. ACM Transactions on Graphics, 2004, 23(3):303-308.

[6] Blake A, Rother C, Brown M, et al. Interactive image segmentation using an adaptive GMMRF model[C]∥Proc of the 8th European Conference on Computer Vision, 2004:428-441.

[7] Rother C,Kologorov V, Blake A.“GrabCut”:Interactive foreground extraction using iterated graph cuts[C]∥Proc of the ACM SIGGRAPH Conference, 2004:309-314.

[8] Xu Qiu-ping, Guo Min, Wang Ya-rong. Fast image segmentation algorithm based on multiscale analysis and graph cuts[J]. Application Research of Computer, 2009,26(10):3989-3991.(in Chinese)

[9] Xu Qiu-ping, Guo Min, Wang Ya-rong. Fast color image segmentation based on watershed transform and graph cuts[J]. Computer Engineering, 2009,35(19):210-215.(in Chinese)

[10] Han S D, Tao W B, Wang D S, et al. Image segmentation based on grabcut framework integrating multiscale nonlinear structure tensor[J]. IEEE Transactions on Image Processing, 2009, 18(10):2289-2302.

[11] Han S D, Tao W B, Wu X L. Texture segmentation using independent-scale component-wise riemannian-covariance Gaussian mixture model in KL measure based multi-scale nonlinear structure tensor space[J]. Pattern Recognition, 2011,44(3):503-518.

[12] Han Shou-dong, Zhao Yong, Tao Wen-bing, et al. Gaussian super-pixel based fast image segmentation using Graph-Cuts[J]. Acta Automatica Sinica, 2011,37(1):11-20.(in Chinese)

[13] Ford L,Fulkerson D.Flows in networks[M] .New Jersey:Princeton University Press, 1962.

附中文參考文獻：

[8] 徐秋平,郭敏,王亞榮.基于多尺度分析與圖割的快速圖像分割算法[J].計算機應用研究, 2009,26(10),3989-3991.

[9] 徐秋平,郭敏,王亞榮.基于分水嶺變換和圖割的彩色圖像快速分割[J].計算機工程, 2009,35(19),210-215.

[12] 韓守東, 趙勇, 陶文兵, 等. 基于高斯超像素的快速Graph Cuts圖像分割方法[J]. 自動化學報, 2011, 37(1):11-20.