一種新的基于直覺模糊Petri網的模糊推理算法*

申蔓蔓，樂曉波，周愷卿

(1.長沙理工大學計算機與通信工程學院，湖南 長沙 410114；2.馬來西亞理工大學計算學院，馬來西亞UTM士古來 柔佛洲 80310)

1 引言

傳統Petri網PN(Petri Nets)理論不能處理非確定信息，使得Petri網在建模、處理和分析不確定系統時缺乏柔性。為了克服這一問題，Lipp L L在1984年提出模糊Petri網的概念。作為Petri網理論與模糊集合理論的有機結合的一種高級拓撲結構，模糊Petri網在不確定知識的表示和推理領域得到了廣泛的應用。近年來學者于不同研究背景提出了不同的模糊Petri網模型和相應的模糊推理算法[1～6]。文獻[1]給出了帶標識的模糊Petri網進行模糊推理，該方法采用了一種改進的相似度，因此計算出推理結果的意義更加明晰。文獻[2]提出了基于區間值的直覺模糊Petri網IFPN(Intuitionistic Fuzzy Petri Nets)模型，使直覺模糊推理在理論上得以實現。文獻[3]基于直覺模糊Petri網理論，建立了空戰戰術決策模型，引入非隸屬度函數，在處理不確定信息時具有更強的表現能力。文獻[4]提出的基于直覺模糊Petri網的意圖識別方法,在推理過程中充分發揮Petri網的動態并行推理能力,使得推理更加高效。文獻[5]提出了一種基于模糊故障樹的模糊Petri網模型，更適合對事故現場進行診斷。文獻[6]基于模糊Petri網的電動機輪子故障診斷，表明模糊Petri網有一個簡單的結構、良好的表達斷層和模糊推理的能力。

但是，隨著對實際問題認識和研究的不斷深入，傳統模糊集合理論不能完整表達所研究問題的所有信息這一缺陷在實際應用過程中越來越突出[7]。因此，在以模糊Petri網為工具進行知識表示和模糊推理的過程中，由于難以獲得足夠的信息導致不能獲得滿意的推理結果。為了克服這一問題，本文試圖將具有較強的表達能力、處理不確定的信息能力的直覺模糊集合引入模糊Petri網理論，給出直覺模糊Petri網(IFPN)的形式化定義[8]，并在基于該模型的推理過程中引入庫所重排策略，提出一種新的基于IFPN模型的庫所重排策略的推理算法，有效簡化模糊推理過程。最后，通過實例檢驗此算法的可行性和有效性。

2 基本定義

2.1 算法所涉及的相關定義

直覺模糊集是保加利亞學者Tanassov K A[9]在模糊集基礎上提出的新概念，增加了一個新的屬性參數—非隸屬度函數，以一個區域值代替了隸屬度，具有更強的模糊描述能力。直覺模糊Petri網是在Petri網的基礎上擴展而來的，它應用的出發點是基于其知識表達和邏輯推理功能。直覺模糊理論在原有Zadeh模糊集理論的基礎上引入直覺模糊集定義，進而可以描述“非此非彼”的“模糊概念”[10]。

定義1(直覺模糊集合) 設X為論域，則X上的一個直覺模糊集合A為：

A={〈x,μA(x),νA(x)〉|x∈X}

其中,μA(x):X→[0,1]，νA(x):X→X[0,1]，且0≤μA+νA≤1,?x∈X,μA(x)表示x對A的隸屬程度，νA(x)表示x對A的非隸屬程度。

定義2(直覺模糊關系) 設X和Y是普通、有限非空集合的論域。定義在直積空間X×Y上的直覺模糊子集稱為從X到Y之間的二元直覺模糊關系。記為：

R={〈(x,y),μR(x,y),νR(x,y)〉|x∈X,y∈Y}

其中,μR:X×Y→[0,1]和νR:X×Y→[0,1]滿足條件0≤μR(x,y)+νR(x,y)≤1,?(x,y)∈X×Y。

定義3(1)乘法算子⊙：

C=A⊙B?C=(μA(x)·μB(x),

νA(y)+νB(y)-νA(y)·νB(y))

(2)加法算子⊕：

C=A⊕B?Cij[max(μA(x),μB(x)),

min(νA(y),νB(y))]

文獻[11]對乘法算子⊙與加法算子⊕做了較詳細的討論。

2.2 IFPN的形式定義及相關規則

為使直覺模糊推理更加方便，本小節在直覺模糊集合的基礎上給出直覺模糊Petri網的定義及其形式化表示。

定義4直覺模糊Petri網可以用一個六元組來表示：

IFPN=(P,T,I,O,M,τ)

其中:

(1)P=PU∪PQ∪PD為IFPN中有限庫所集合，每一個庫所對應著一個命題。為使直覺模糊推理更高效，本文給出了庫所的重排：

P=PU∪PQ∪PD

其中,PU={p1,p2,…,pm1}代表初始庫所，PQ={q1,q2,…,qm2}代表中間庫所，PD={d1,d2,…,dm3}代表結論庫所，m=m1+m2+m3為總庫所數。

(2)T={t1,t2,…,tm}為IFPN中變遷的集合，每個變遷對應一個規則。

(3)In×m={aij|pi∈P,tj∈T}，i=1,2,…,n;j=1,2,…,m,其中aij∈[0,1]表示庫所pi到變遷tj的輸入權重。

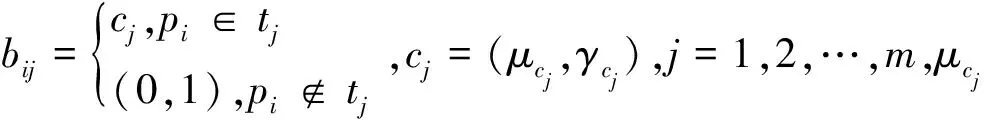
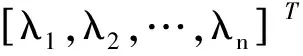
(6)S:P→[0,1]為庫所P的一個關聯函數，表示庫所P對應的命題的模糊標識值，初始標識S0=[S0(p1),S0(p2),…,S0(pn)]T，其中S0(pi)為直覺模糊數(u0i,y0i)。

用直覺模糊Petri網的變遷來表示直覺模糊產生式規則，變遷的輸入表示規則的前提，變遷的輸出庫所表示規則的結論，通過閾值來控制變遷的發生，并用變遷的置信度表示模糊規則的可信度。與普通模糊Petri網產生式規則不同的是，直覺模糊Petri網產生式中的這些量都是用直覺模糊集表示的，具體模型有以下三種類型[11]：

類型1簡單直覺模糊產生式規則。

IFaTHENb (CF=c)

其中，a是前提命題，b是結果命題，p1為變遷t的輸入庫所，p2為變遷t的輸出庫所，c為規則的可行度，M1表示輸入庫所中的標識，M2表示輸出庫所中的標識。該類型直覺模糊Petri網表示如圖1所示。

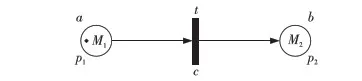
Figure 1 Corresponding IFPN model of simple IFPR圖1 簡單IFPR的IFPN表示

類型2合取直覺模糊產生式規則。

IFa1ANDa2AND…ANDanTHENak( CF=c, τ)

其中前提命題a1，a2，…，an分別由庫所p1，p2，…，pn代替，結果命題由ak代替，該類型的直覺模糊Petri網表示如圖2所示。

Figure 2 Corresponding IFPN model of ‘and’ IFPR圖2 合取式IFPR的IFPN表示

類型3析取直覺模糊產生式規則。

IFa1ORa2OR…ORanTHENak(CF=c1, CF=c2,…, CF=cn)

該類型的直覺模糊Petri網表示如圖3所示。

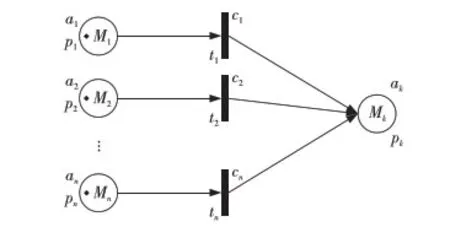
Figure 3 Corresponding IFPN model of ‘or’ IFPR圖3 析取式IFPR的IFPN表示

3 基于IFPN模型的推理算法

直覺模糊Petri網(IFPN)將直覺模糊集合引入模糊Petri網理論，在基于該模型的推理過程中引入庫所重排策略，并利用可激活變遷判斷計算公式對推理的每一步進行可激活變遷判斷，提出一種新的基于IFPN模型的庫所重排策略的模糊推理算法，有效簡化了模糊推理過程，提高了算法的時間效率。其算法處理過程如下。

在IFPN模型中，每一步推理過程的模型的有關數據描述：

輸入：輸入矩陣Ii×j、變遷閾值τj、初始標識向量S0：

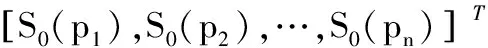
輸出：輸出矩陣Oi×j、庫所的標識向量S：

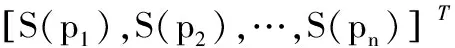
步驟1初始化，令K=0，I=(0,1)，此處(0,1)為每個元素均為直覺模糊數(0,1)的矩陣。

步驟2判斷重排后的庫所對應的變遷(初始庫所PU對應變遷和中間庫所PQ對應的變遷)能否發生。判斷變遷是否可激活的計算公式如下：

如果

(1)

則變遷tj可激活。

判斷有無可激活變遷，若無變遷可激活，則第K步推理結束，跳過步驟3和步驟4，進入步驟5；否則，激活可激活變遷tj，繼續執行步驟3。

步驟3計算變遷tj激活后各個庫所的可信度:

合取：

(2)

析取：

(3)

步驟4更新所有庫所可信度:

SK+1(pn)=SK(pn)⊕SK+1(pn)

(4)

步驟5判斷推理過程是否還有第K+1步，若是，則令K=K+1，返回步驟2；否則推理結束。

上述算法在采用庫所重排策略的過程中，步驟2對第K步系統中可激活的變遷進行有效判斷，每一步只對可激活變遷進行計算處理，從而避免了對系統中全部變遷進行計算，簡化了推理過程，節省了推理時間。

上述算法的框圖描述如圖4所示。

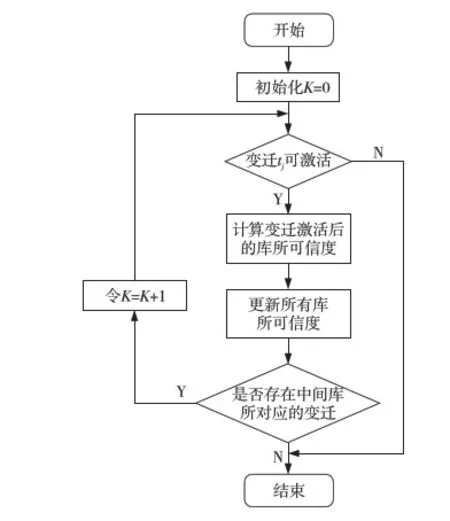
Figure 4 Flowchart of the proposed reasoning algorithm using IFPN圖4 基于IFPN模型的推理算法框圖描述

4 實例分析

這里采用文獻[8]中汽車發動機故障診斷的實例以驗證本文所提出的算法的可行性和有效性，為編程方便，本文將原實例中庫所p5和p6的位置交換，使編程中的參數取值能連續。

關于汽車發動機故障診斷的推理規則如下：

R1：IFV1(0.7)ANDV2(0.2)ANDV3(0.3)THEN(τ1=(0.4，0.55)) V6(CF=(0.8，0.18))

R2：IFV1(0.7)ANDV4(0.3)THEN(τ2=(0.4，0.58)) V7(CF=(0.8，0.15))

R3：IFV5(1.0)THEN(τ3=(0.3，0.66)) V8(CF=(0.9，0.1))

R4：IFV6(0.7)THEN(τ4=(0.3，0.67)) V8(CF=(1.0，0.0))

其中，V1表示蓄電池電壓過低，V2表示點火時間過晚，V3表示進氣系統漏氣，V4表示節氣門不能關閉，V5表示發動機回火，V6表示發動機轉數不良，V7表示發動機加速不良，V8表示發動機不能啟動。

該組規則的IFPN推理模型如圖5所示。

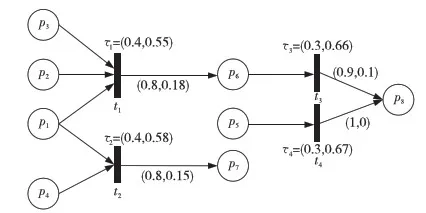
Figure 5 IFPN model of the case study圖5 IFPN推理模型

推理過程如下：

首先，令K=0，I=(0，1)，根據IFPN模糊推理算法輸入輸入矩陣Ii×j，輸出矩陣Oi×j、初始標識S0以及變遷閾值τ：

輸出矩陣Oi×j=

初始標識S0=[(1,0) (0.2,0.78) (0.3,0.69) (0.8,0.18) (0,1) (0,1) (0,1) (0,1) ]T

變遷閾值τ= [(0.4,0.55) (0.4,0.58) (0.3,0.66) (0.3,0.67)]T

(1)利用式(1)判斷變遷t1、t2可激活，利用式(2)～式(4)計算得：

S1=[(1,0) (0.2,0.78) (0.3,0.69) (0.8,0.18) (0,1) (0.504,0.478) (0.752,0.2) (0,1)]T

(2)利用式(1)判斷變遷t3可激活，利用式(2)～式(4)計算得：

S2=[(1,0) (0.2,0.78) (0.3,0.69) (0.8,0.18) (0,1) (0.504,0.478) (0.752,0.2) (0.454,0.53)]T

(3)利用式(1)判斷無變遷可激發，因此推理結束，此時，IFPN輸出的庫所標識向量為：

S2=[(1,0) (0.2,0.78) (0.3,0.69) (0.8,0.18) (0,1) (0.504,0.478) (0.752,0.2) (0.454,0.53)]T

從推理結果可以看出，隸屬度最大并且非隸屬度最小的庫所的標識為p7=(0.752,0.2)，這個結果與表1所示文獻[8]中采用的推理算法計算的結果一樣，但其計算過程明顯簡潔。文獻[8]中步驟3為判斷各個變遷的狀態轉移函數值是否大于之前的最大狀態轉移函數值，即每次計算變遷轉移函數值后，都要重新判斷各個變遷的狀態函數值是否大于之前的狀態函數值；而本文提出的算法因采用了庫所重排策略有效地避免對未激發變遷的判斷，從而大大節省了推理時間，提高了計算效率。

Table 1 Simulation results of reference[8]

5 結束語

本文提出了一種基于直覺模糊Petri網的庫所重排策略及其相關的模糊推理算法，有效地提高了推理速度和推理效率。從表1可以看出，與文獻[8]的推理算法比較，本文所設計的推理算法可得到同樣精確的結果，本文的推理過程只有五步而文獻[8]有八步，且文獻[8]每次計算一個變遷轉移函數值后都要重新考慮所有變遷是否發生，而本文只需判斷此時還未產生的變遷是否能被激活，從而有效地簡化了推理過程，節省了推理時間，降低了算法的時間復雜度。由此可見，本文所提出的基于IFPN模型的推理算法為模糊推理的研究提供了一個新的途徑，此算法的可行性與正確性已在VisualC++6.0環境下得到了驗證。

[1]SunXiao-ling,WangNing,LiangYan,etal.FuzzyreasoningbyusingmarkedfuzzyPetrinets[J].ComputerEngineering&Science, 2012, 34(3):152-157.(inChinese)

[2]HanGuang-chen,SunShu-dong,SiShu-bin,etal.ResearchonfaultdiagnosissimulationbasedonfuzzyprobabilityPetrinetssystem[J].ComputerIntegratedManufacturingSystems, 2006, 12(4):520-525.(inChinese)

[3]ZhangYing,YangRen-nong,WuMeng,etal.Aircombattacticsdecision-makingbasedonintuitionisticfuzzyPetrinet[J].ComputerEngineeringandApplications, 2012, 48(30):224-228.(inChinese)

[4]ZhouChuang-ming,ShenXiao-yong,LeiYing-jie.ResearchoffoeintentionrecognitionmethodbasedonintuitionisticfuzzyPetrinet[J].ComputerApplication, 2009, 29(9):2464-2467.(inChinese)

[5]LuQ,HuangG,ZhuH.FuzzyanalysisofaccidentsdiagnosisbasedonfuzzyPetrinet[J].InternationalJournalofSystemsControl, 2007, 2(3):228-236.

[6]TianxuJ,GeZ.AmethodforfaultdiagnosisintestsystemofelectricmotorwheelsbasedonFuzzyPetrinet[C]∥Procofthe31stControlConference(CCC), 2012:5240-5244.

[7]QiaoF,WuQ,LiL,etal.AfuzzyPetrinet-basedreasoningmethodforrescheduling[J].TransactionsoftheInstituteofMeasurementandControl,2011,33(3-4):435-455.

[8]SunXiao-ling,WangNing.WeightedintuitionisticfuzzyreasoningbasedonintuitionisticfuzzyPetrinets[J].ComputerEngineeringandApplications, 2013, 49(4):50-53.(inChinese)

[9]ShenX,LeiY,LiC.IntuitionisticfuzzyPetrinetsmodelandreasoningalgorithm[C]∥Procofthe6thInternationalConferenceonFuzzySystemsandKnowledgeDiscovery, 2009:119-122.

[10]LiaoWei-zhi,GuTian-long,LiWen-jing,etal.ModelingandschedulingforfuzzyflexiblemanufacturingsystembasedonhybridPetrinets[J].ComputerIntegratedManufacturingSystems, 2008, 14(11):2134-2141.(inChinese)

[11]VardevaI,GochevV.Calculationofestimationsofmessagesbygeneralizednetsandintuitionisticfuzzytruthvalues[C]∥Procofthe6thIEEEInternationalConferenceonIntelligentSystems, 2012:242-245.

附中文參考文獻：

[1] 孫曉玲,王寧,梁艷,等.應用帶標識的模糊Petri網的模糊推理[J].計算機工程與科學,2012,34(3):152-157.

[2] 韓光臣,孫樹棟,司書賓,等.基于模糊概率Petri網系統的故障診斷仿真研究[J].計算機集成制造系統,2006,12(4):520-525.

[3] 張瀅,楊任農,鄔蒙,等.直覺模糊Petri網的空戰戰術決策[J].計算機工程與應用,2012,48(30):224-228.

[4] 周創明,申曉勇,雷英杰.基于直覺模糊Petri網的敵意圖識別方法研究[J].計算機應用,2009,29(9):2464-2467.

[8] 孫曉玲,王寧.基于直覺模糊Petri網的加權直覺模糊推理[J].計算機工程與應用,2013,49(4):50-53.

[10] 廖偉志,古天龍,李文敬,等.模糊柔性制造系統的混雜Petri網建模與調度[J].計算機集成制造系統,2008,14(11):2134-2141.