基于駛出成功率的高速公路出匝車輛行駛模型

崔洪軍，馬新衛，李霞，李霖

（河北工業大學土木工程學院，天津 300401）

基于駛出成功率的高速公路出匝車輛行駛模型

崔洪軍，馬新衛，李霞，李霖

（河北工業大學土木工程學院，天津 300401）

通過建立出匝車輛行駛模型，研究了高速公路出匝車輛的行駛特征．建立了出匝車輛的變道過程模型，并結合主線車輛分布特點，研究了車輛的最小可變道間隔與出匝成功率．研究表明，交通流適中，三車道最內側駕駛員駛出高速公路可用距離為1 000 m左右時，駛出成功概率可達到90%，且之后逐漸趨于平穩；當可用距離低于600 m時，駛出成功率低于60%．若要繼續保持或追求較高的出匝成功率，出匝車輛可用距離應依照曲線適當增加，且車流量越高，駛出成功率的提升難度越大．

交通工程；出匝車輛行駛模型；概率論與數理統計；車輛變道；最小可變道間隔；駛出成功率

高速公路是一種現代化的公路運輸方式，維持高速公路暢通高效的運行，能有力地保障國民經濟的持續穩定發展．高速公路基本段交通流比較穩定，一般均可達到設計要求，而分流區，尤其是出匝處及其影響區域內，由于機動車車道更換、速度加減不定、駕駛員駕駛特征復雜多變等因素，成為影響高速公路安全高效運營的瓶頸．因此，對出匝分流區內機動車行駛規律進行研究很有必要．

國內學者劉偉銘等通過進行大量實地調查，應用微分法對出匝車輛模型進行了分析[1]；郭唐儀等通過構建機動車出匝模型并運用TSIS-CORSIM模擬來分析車輛行駛特征以及AGS合理設置位置[2]；魏麗英等運用線性跟馳模型理論對車頭時距與車道變換進行了研究，并通過模擬加以驗證[3]；詹盛等采用模糊聚類分析對車輛的車道變換過程進行了研究[4]．本文通過建立出匝車輛模型，重點分析機動車出匝變道行為，引入了出匝成功率，對不同道路條件下出匝成功率與出匝車輛行駛距離的關系進行了研究，以期為高速公路出匝分流區的規劃設計、道路信息指示系統、駕駛員安全駕駛引導等方面提供依據．

1 駛出模型建立

1.1 駕駛員駛出高速公路行為分析

根據日常駕駛經驗，機動車駕駛員決定變道后，首先會降低機動車的行駛速度，并保持低于右側車輛的某一速度，進入等待變道過程，當駕駛員發現右側存在滿足變道要求的兩車間隔之后，便會立即進行變道行為，直至完全變入另一車道，一次變道完成，然后進入下一次變道過程．機動車變道至最外側車道時，會經歷一個減速過程，以保證能以安全的速度進入匝道．至此，整個駛出過程結束．

1.2 模型建立的前提假設

1）所有駕駛員的駕駛特征和變道規則相同，且均符合安全駕駛；2）除變道車輛以外的所有車輛以不變的分布形式行進，且不與所研究車輛同時發生變道行為；3）不考慮車長影響；4）根據規范，減速車道漸變率約為1/20[5]，偏移角度較小，故模型建立時未考慮減速車道漸變率．

1.3 駛出模型

以三車道最內側車輛駛出高速公路過程為例（圖1）．其中第1次變道過程為從A點到D點，第2次變道過程為從D點到G點，G點到H點是駛出高速公路車輛的減速過程．Sa為車輛進行出匝行為的可用距離．

A點到B點過程是變道車輛的減速過程，變道車輛于B點處達到略低于右側車道車輛實際車速的速度，然后保持該速度等待變道機會．行駛至C點時發現臨近車道車輛之間的可變道間隔，并立即變換車道，于D點處結束變道過程，然后進入下一次變道過程，最終在G點處，變道車輛完成變道過程．車輛在G點至H點進行減速過程，以保證車輛能夠以安全速度進入匝道．當車輛駛入匝道后，完成整個駛出高速過程．

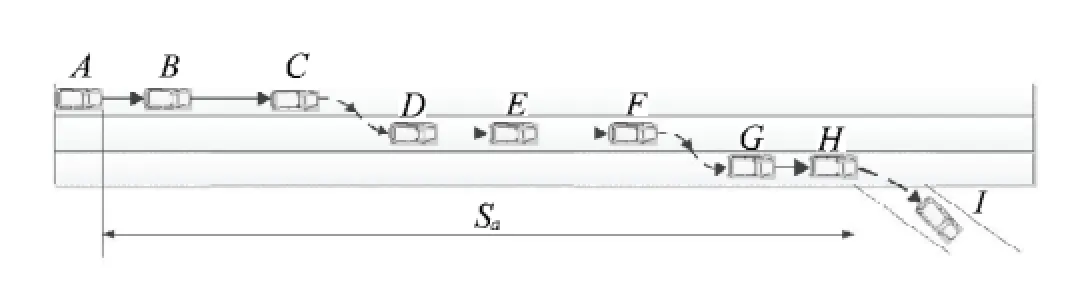
圖1 高速公路出匝車輛行駛模型Fig.1 Vehicle driving out of freeway model in off-ramp diverging area

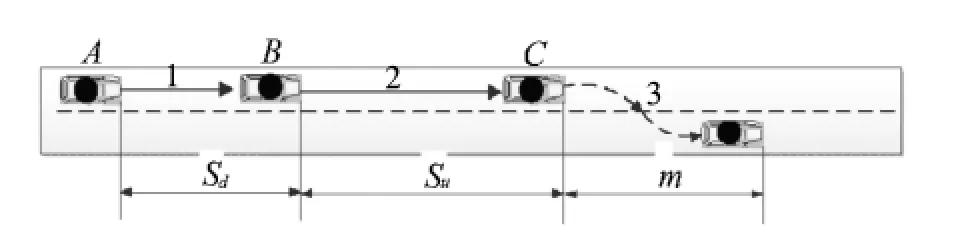
圖2 出匝車輛變道模型Fig.2 Vehicle lane-changing model in off-ramp diverging area

2 機動車變道模型分析

機動車變道過程占整個駛出過程的絕大部分，因此對機動車變道行為建立模型以進行科學合理的分析是本研究內容的關鍵．以從第i條車道向第i+1條車道進行一次變道的過程為例（圖2）．

1過程是車輛的減速過程，根據模型，可得

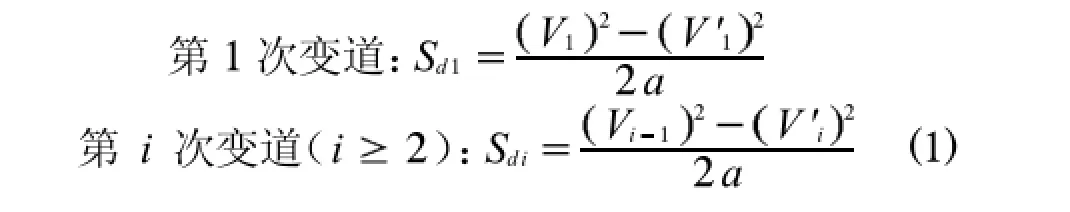
Vi為第i條車道車輛車速（取85%車位速）；V'i為機動車行進在第i條車道上等待變道過程中的行駛速度；a為減速度（根據文獻研究成果，取0.6 g[2]，g=9.8 m/s2）；Vr為匝道車輛行駛速度．

2過程是車輛保持勻速等待變道機會的過程．以臨近車道三角標記車輛為參考系，則有圖3模型．

di為第i條車道上車輛之間的平均間隔．3過程是車輛變換車道的過程．

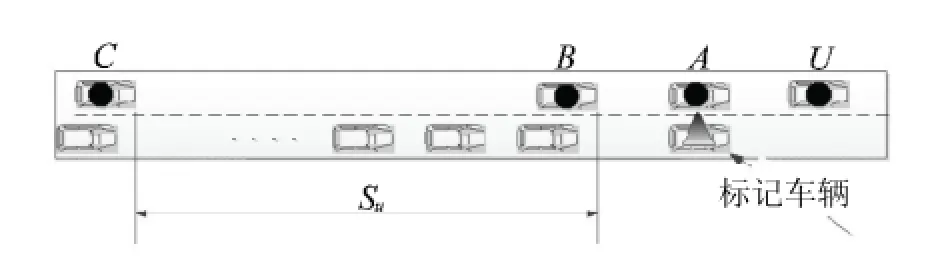
圖3 變道車輛等待變道過程Fig.3 The process of waiting for opportunity to change lane

通過查閱相關資料與詢問有高速公路駕駛經驗的司機，汽車行駛在高速公路，速度在80 km/h左右時，車輛進行緩慢變道方向盤約轉動1/8圈，汽車轉向5°左右．忽略駕駛員操作方向盤所需的時間，實際進行變道過程可以簡化為圖4．則有

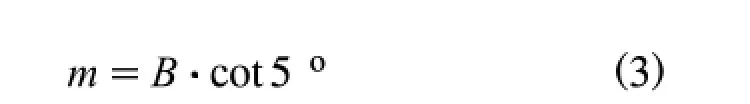
式中：m為車道變換過程所需距離；B為車道寬度（根據規范，取3.75 m[5]）．

綜合上述分析，設變道車輛駛出高速公路過程中共需要變道k次，則整個駛出過程中所需距離為

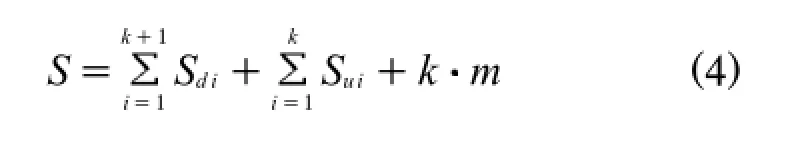
3 可變道間隔研究

可變道間隔是能滿足相鄰車道變道車輛變道需求的車輛間隔，可變道間隔的大小直接影響到機動車變道過程所需距離，因此對機動車可變道間隔進行研究對變道模型以及駛出模型尤為重要．本文通過建立變道車輛完成時刻車距模型，對車輛可變道間隔進行分析．

3.1 變道車輛變道完成時刻車距模型

N車為剛完成變道過程的車輛，此時刻（t時刻）與前車即N+1車保持距離1，若N+1車在此時刻遇到情況進行減速，N車經過一段反應時間后也進行減速，當2車均靜止時（t'時刻）若能保證保持安全距離l，則說明1符合N車與N+1車保持的安全距離要求，N車能夠安全變道至N+1車后面，如圖5．

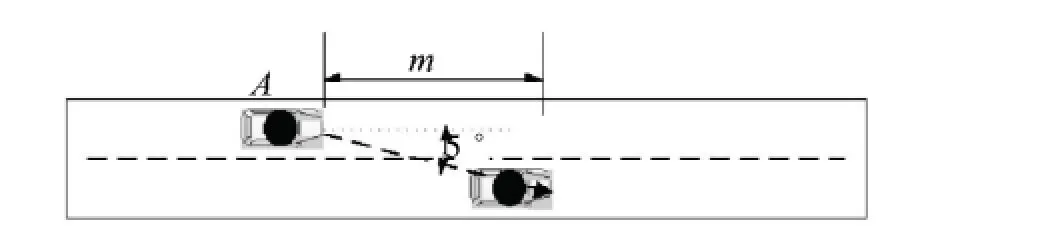
圖4 機動車變換車道簡化過程Fig.4 The simplified process of vehicles'changing lane behavior

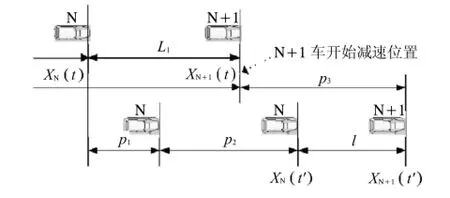
圖5 變道車輛與前車距離模型Fig.5 The model of the distance between the vehicle and the one forward

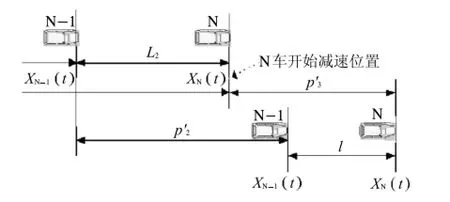
圖6 變道車輛與后車距離模型Fig.6 The model of the distance between the vehicle and the one backward

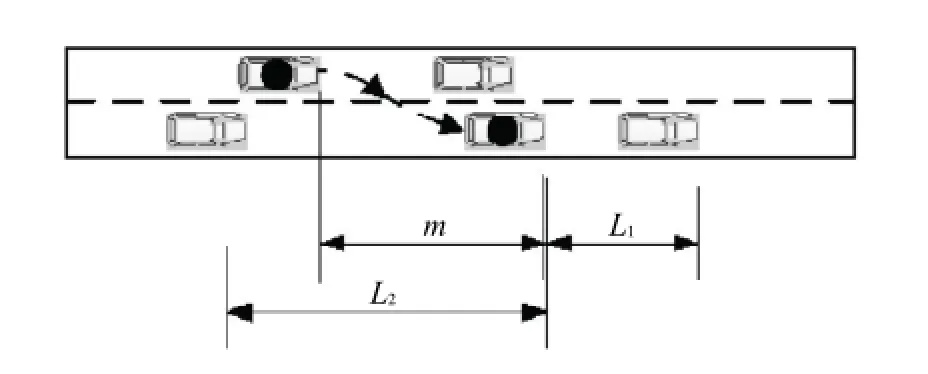
圖7 安全變道過程Fig.7 The process of changing lane safely

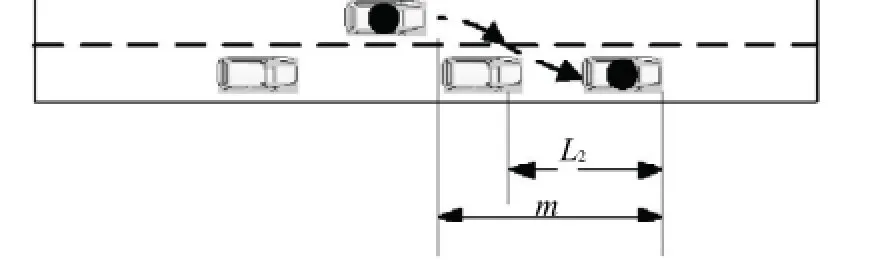
圖8 不安全變道過程Fig.8 The process of changing lane unsafely

式中：VN為N車車速；L1為前后臨近2車在t時刻間距；Xit為i車在t時刻所處位置；p1為N車反應過程行駛距離；p2為N車制動距離；p3為N+1車制動距離；l為2車靜止后保持的安全距離（根據文獻研究成果，一般為2～5 m，取5 m[3]）；L2為前后臨近2車在t時刻的間距；p'2為N 1車的制動距離；p'3為N車的制動距離；其中反應時間為tf．此處出于安全考慮，tf取2.5 s[6]，其中判斷時間1.5 s，運行時間1 s．

3.2 最小可變道車輛間隔確定

機動車變道之后至少需要與前車保持L1的距離并與后車保持L2的距離機動車才屬于安全變道，且機動車駕駛員只有在確保安全的情況下才會進行變道．與此同時，車輛變道之后后車的跟車距離L2需大于m，才能保證機動車在變道過程中不刮蹭到后車．

設車輛可變道的臨近車頭間距的最小間距為Smin，則有

3.3 可變道間隔修正系數

為了使可變道車頭間距更加符合實際，采用事先標記觀測路面，在跨線橋中心處視頻錄像并進行后期分析的方法，得到相關數據，以期對此部分計算模型結果進行修正．觀測調查選在3月18日進行，調查時段為7:00～11:00，共得到37組數據．根據計算模型，變道速度與可變道機動車間隔屬于二次相關，MATLAB軟件對數據進行回歸分析得到

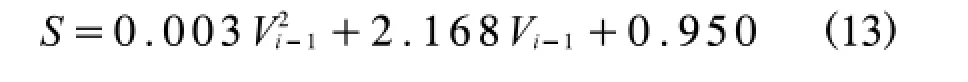
將調查值與模型計算值進行比較得到表1．

對比2組數據發現，實際值略小于模型計算值，原因是變道車輛進行變道時會提前打開轉向燈對后車進行提醒，后車看到提示會自覺進行減速，為前車預留足夠的空間進行變道．引入修正參數=0.8，以對可變道最小間隔進行修正．

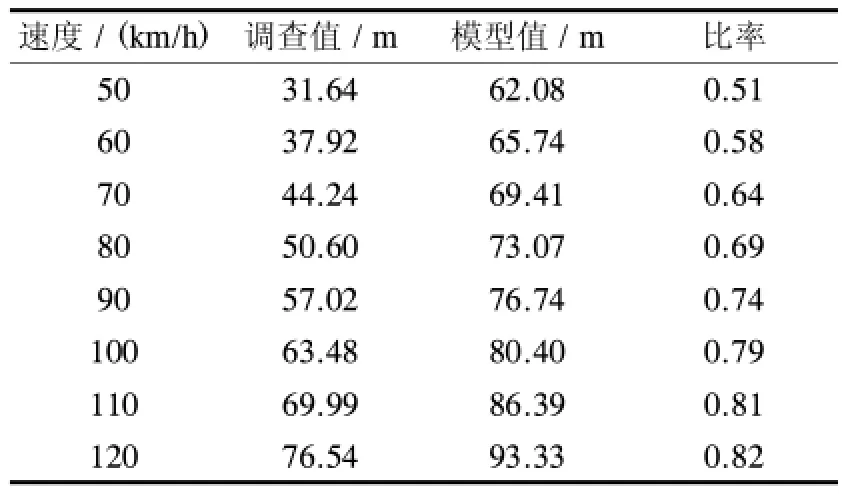
表1 調查值與模型計算值對比表Tab.1 The contrast table of the investigation value and the calculation value

3.4 可變道間隔出現概率分析

已知第i條車道的車流量qi與該條車道的實際車速Vi，可得每單位距離內的車輛數量，進而可求得Sui內的平均車頭間距為

調查表明，車流密度不大且不受到其余因素影響的情況下，車輛到達基本服從泊松分布[7]．高速公路路段上的交通量一般較城市道路路段交通量小，因此可以用泊松分布描述模型中車輛的到達．可以得出結論，車頭間距服從參數為的負指數分布．其中負指數分布的期望為平均車頭間距di．則可得車頭間隔dik的概率分布為

4 出匝過程可用距離與駛出成功率關系研究

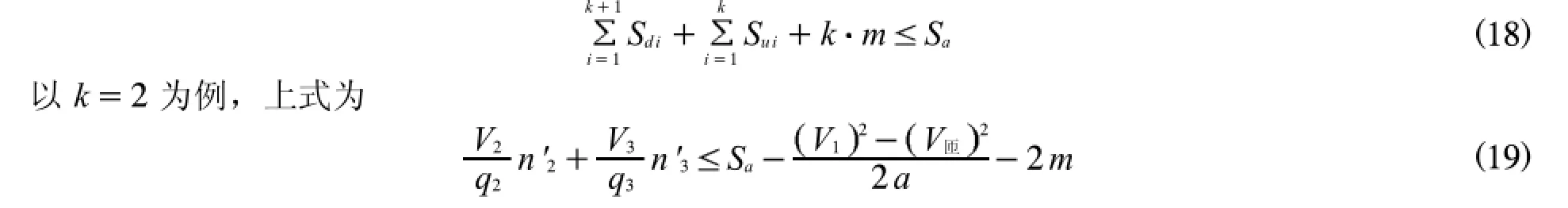
式(19)中，Vi，V匝，Sa，qi，a，m均可根據調查以及實驗求得具體數值，則上式便是關于n'2與n'3的條件不等式，即n'2與n'3滿足上式條件時，三車道最內側車道車輛才能安全駛出高速公路．

由于n'2與n'3的取值是離散分布且相互獨立的，據此可以建立n'2與n'3分布的聯合分布律，如表2．

將聯合分布律中的每點概率放入圖表中對應點處，條件直線與n'2=0，n'3=0所形成的三角形內所有概率之和，即為駛離高速公路車輛在該限定距離內可以成功駛出的成功概率．

表2 n'2與n'3聯合分布率Tab.2 The Joint distribution rate of n'2and n'3

5 實例分析

以k=2為例進行分析，取三車道車流量q=33 000 pcu/D，平均分配到每條車道上，即q1=q2=q3=11 000 pcu/D．根據對多條雙向六車道高速公路上行駛車輛進行觀測記錄，取V1=110 km/h，V2=80 km/h，V3=60 km/h，V'1=60 km/ h，V'2=40 km/h，V匝=30 km/h．

對得出數據進行多項式擬合可得該種道路條件下，S限與最內側車輛駛出成功率之間的數量關系為

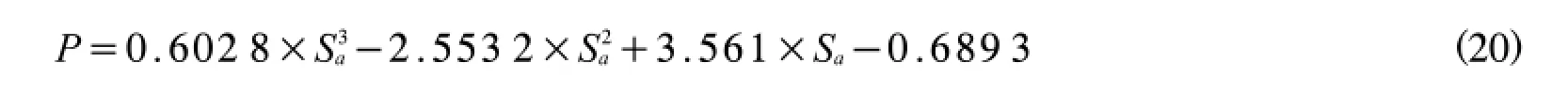
同理可求得不同車流量條件下Sa與駛出成功率P之間關系，如圖9所示．

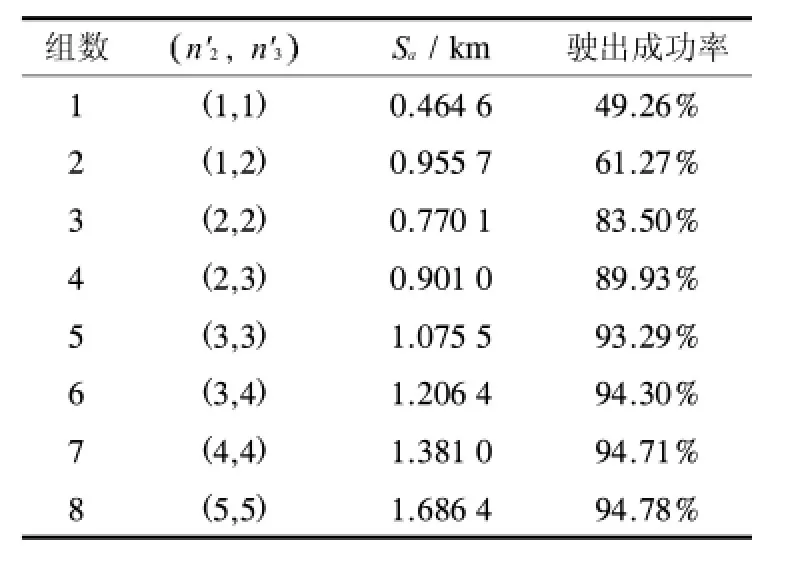
表3 實例分析結果Tab.3 The result of examples of the model

6 結語

對所得關系方程以及曲線進行分析可知，在交通流適中的條件下，三車道最內側駕駛員駛出高速公路可用距離為1000 m左右時，成功概率可達到90%，且在90%之后駛出成功率逐漸趨于平穩；當低于600 m時，駛出成功率低于60%，駛出車輛有可能采取強行變道、嚴重降低車速等行為，造成不同程度的交通沖突，甚至引發交通事故．若要繼續保持或追求較高的出匝成功率，出匝車輛的可使用距離應依照曲線適當增加，且車流量越高，駛出成功率的提升難度越大．此結論可為我國高速公路匝道分流區規劃設計、道路指示標志的放置、駕駛員安全駕駛的引導提供參考依據．

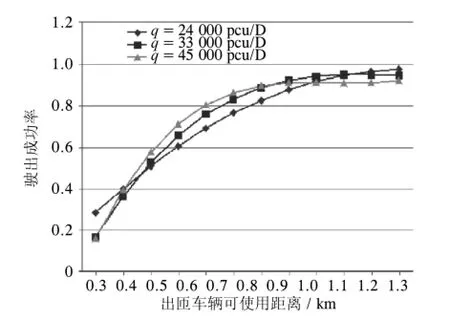
圖9 出匝成功率與出匝可用距離關系圖Fig.9 The relationship between P and Sa

[1]劉偉銘，鄧如豐，張陽．高速公路出匝分流區超車道車輛車道變換模型[J]．公路交通科技，2012，29（8）：106-111．

[2]郭唐儀，胡啟洲，姚丁元．高速出口預告指路標志設置距離及其安全性能比較[J]．公路交通科技，2011，28（12）：106-111．

[3]魏麗英，雋志才，田春林．駕駛員車道變換行為模擬分析[J]．中國公路學報，2001，14（1）：79-82．

[4]詹盛，徐遠新，石涌泉．基于模糊聚類分析的車道變換階段劃分[J]．計算機工程與設計，2013，34（9）：3293-3297．

[5]JTJ B01-2014，公路工程技術標準[S]．

[6]徐錦強，陳竹師，丁藝．基于駕駛行為的車道變換模型研究及仿真[J]．華東交通大學學報，2011，28（6）：68-72．

[7]Texas Transportation Institute．Sign Crew Fiek l Book:A Guide to proper Location and Installation of Signs and Other Devices[M]．Houston: Texas Department of Transportation，2007．

[8]LI J，CHIMBA D．A Supplement to Advance Guide Sign Placement Distance in MUTCD[C/CD]//Transportation Research Board 85th Annual M eeting Compendium of Papers．Washington D C：Transportation Research Board，2006．

[責任編輯 楊屹]

Vehicle driving out of freeway model in off-ramp diverging area based on driving-out success rate

CUI Hongjun，MA Xinwei，LI Xia，LI Lin

(School of Civil Engineering,Hebei University of Technology,Tianjin 300401,China)

By establishing the vehicle driving out of freeway model,the driving pattern of the vehicles in off-ramp diverging area was analyzed.According to the distribution of the vehicles on the main lane,the vehicle lane-changing model in off-ramp diverging area was established,and the m inimum lane-changeable time headway and the driving-out success rate were researched.The result indicates that,w ith a medium traffic volume,w hen the available distance for the driving-out vehicle reaches 1 000 m,the driving-out success rate can be 90%and more,and the grow th tendency gradually decreases;when the distance is below 600 m,the success rate is lower than 60%.In order to pursue a higher driving-out success rate,w ith the increase of the traffic volume,the available distance for driving-out vehicles should be added,and the promoting difficulty increases.

transport engineering;vehicle driving-out model;probability theory&mathematical statistics;vehicle lanechanging;the minimum lane-changeable interval;driving-out success rate

U491

A

1007-2373(2015)06-0081-05

10.14081/j.cnki.hgdxb.2015.06.016

2015-05-20

河北省自然科學基金（E2013202228）；河北省交通廳科技計劃（R070245）

崔洪軍（1974-），男（漢族），教授．

數字出版日期：2015-12-17數字出版網址：http://www.cnki.net/kcms/detail/13.1208.T.20151217.1510.010.htm l