一類帶馬爾科夫參數的不確定性系統魯棒控制器設計

王瑾，董澤

（華北電力大學 控制科學與計算機學院，河北 保定 071002）

現實系統中往往存在許多不確定因素，將這些不確定因素建模為隨機過程可以使系統更真實、更準確地反映實際工程技術中的系統運動規律，但是參數的不確定性又會影響系統控制性能的穩定性以及其他性能［1］，因此，要在系統中引入魯棒控制確保不確定系統的穩定性.而馬爾科夫跳變系統是一類系統模態受馬爾科夫鏈約束的混雜線性系統，其連續特性和離散特性并存［2］.實際工業過程中，由于外界工作環境變化、參數發生變化、元件失效及連接中斷等突發因素會造成系統結構的變化，馬爾可夫跳躍系統能夠描述此類具有結構突變的實際工業過程而獲得了廣泛的關注研究.此外，在工程實踐中，采用現代控制理論方法所設計的控制系統一般難以達到期望的性能，穩定性也難以保證，而魯棒控制理論基于外部擾動不確定性與系統模型參數不確定性的考慮下，對系統魯棒穩定性問題進行研究，彌補了現代控制理論需精確數學模型的缺點，使系統的分析方法更加有效和實用［3］.本文研究的帶有馬爾科夫參數的不確定系統，可以較好地體現實際系統的特性，對于隨即參數的控制有較好的探究意義.本文通過得到系統的穩定性條件來設計魯棒控制器，完成對結構具有復雜性和突變性的系統的更好控制.

1 不確定性系統

1.1 帶有馬爾科夫跳變參數的不確定性系統模型

對于實際控制對象，尤其是隨機性較強的對象，較難得到準確模型或模型形式復雜，以Markovian跳變系統來描述控制對象會有較好的效果.狀態空間的不確定性模型［4］.

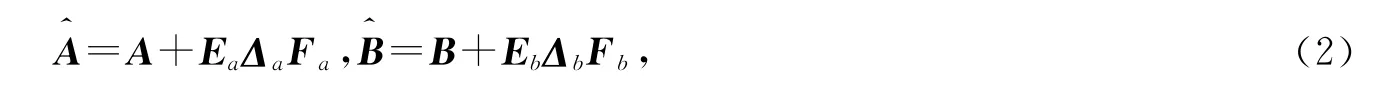
其中，A，B 是適當維數的實常數矩陣，描述了系統的名義模型，即忽略了模型的不確定性后得到的系統模型；Δa和Δb是不確定參數矩陣，反映了系統模型中的參數不確定性，且其中的一些不確定參數可能是重復的；Ea，Eb，Fa，Fb是適當維數的常數矩陣，它們反映了不確定參數是如何影響系統模型的，即反映了模型不確定性的結構.模型的不確定參數盡管是未知的，但總可以設定它們在某個有界的范圍內變化，這個變化范圍的大小直接影響到系統性能.

系統模型（2）中的不確定因素可寫成

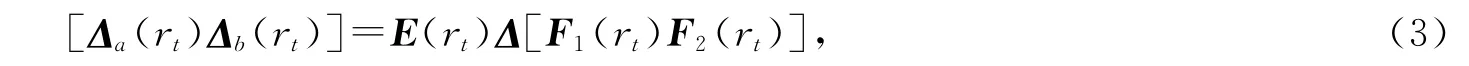
其中ΔTΔ≤I，rt為馬爾科夫跳變參數.

1.2 模型的自由系統

對于系統（1），當u（t）＝0時，系統為自由系統，在自由系統中，不確定部分為0時，系統為名義系統［5］，魯棒穩定性研究即是研究自由系統的穩定性，考慮自由系統

其中，x∈Rn是系統的狀態向量為實常數向量的函數.所要研究的問題是：給出系統（4）的魯棒穩定條件，在該條件下，對于所有不確定參數，系統都是漸進穩定的.

2 系統的魯棒控制器設計

2.1 魯棒穩定性條件

已知系統模型，要想進行控制器的設計，首先要得到其穩定性的條件.根據模型表達式，選擇Lyapunov穩定判據進行求取，因此有以下定理：

定理1 系統（4）對于任意參數ε＞0，存在線性矩陣不等式

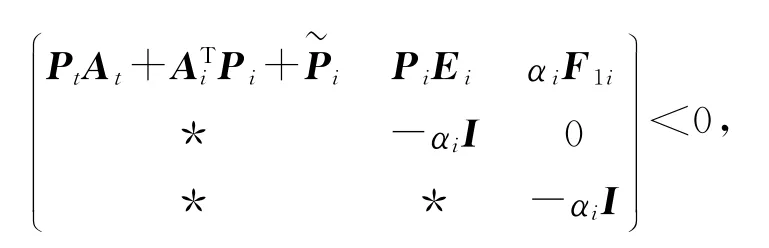
則可知系統魯棒穩定［6］.

證明：已知系統（4）為自由系統模型，設Lyapunov能量方程為V（x）＝xT（t）Pix（t），對能量方程進行弱微分，可得

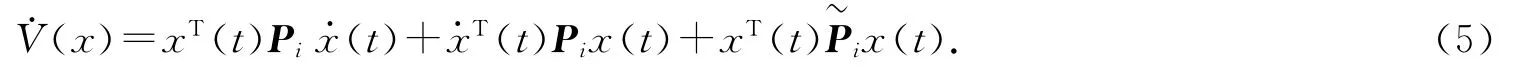
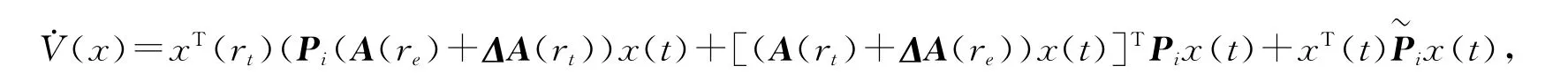
將不確定因素和確定因素分開，得到

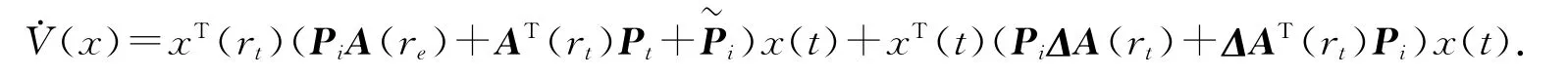
在下文中，以Ai，Ei，Fi代替A（rt），E（rt），F（rt）.由式（3）可知上式中的不確定因素可以寫成

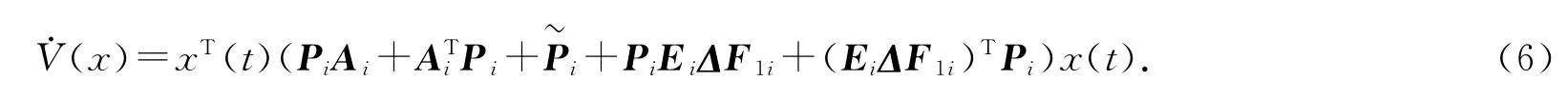
定理2［7］對于給定對稱矩陣Q，適當維度矩陣D，E 和F（t），若存在Q＋DF（t）E＋（DF（t）E）T＜0，對所有滿足FT（t）F（t）≤I的矩陣F（t）成立，則當且僅當存在一個標量ε＞0，有Q＋εDDT＋ε－1ETE＜0.

即

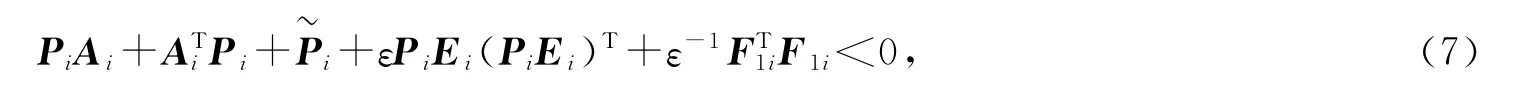
定理3［7］對于如下的線性矩陣不等式，

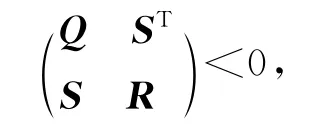
其中Q＝QT，R＝RT，S 為適當維度的矩陣，其等價于R＞0，Q＋STR－1S＞0.

由定理3可知，式（7）可寫成

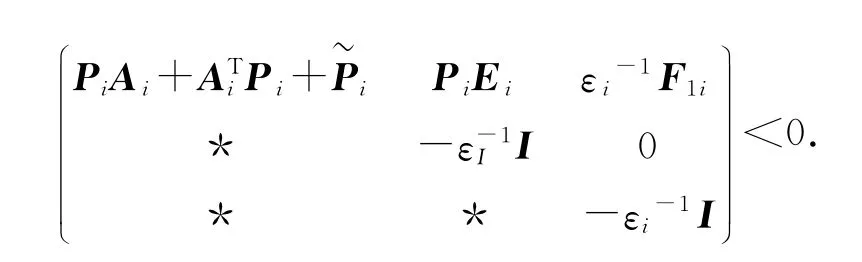
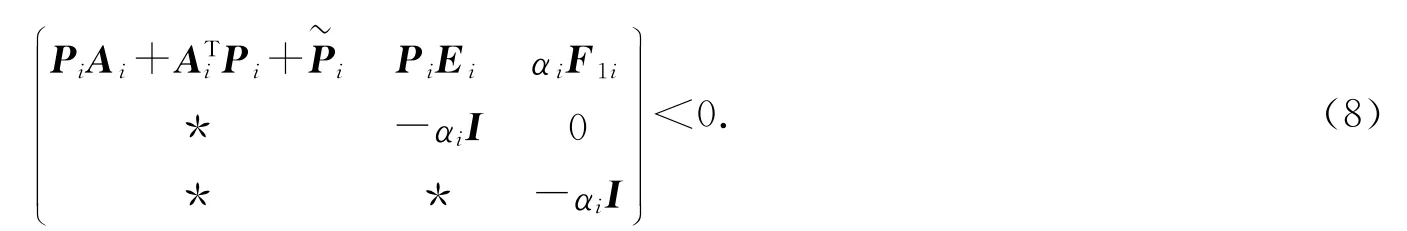
由式（8）可知，可以證明該不等式為系統的魯棒穩定性條件。

2.2 魯棒控制器的設計

已知系統的魯棒穩定性條件，要進行控制器設計，在自由系統基礎上要考慮系統的輸入部分，因此有以下定理：

定理4 對于給定的Ai＞0，如果存在矩陣Xi，Yi滿足，那么控制器是存在的［8］，且控制器形如

證明：已知連續跳變Markovian系統模型為

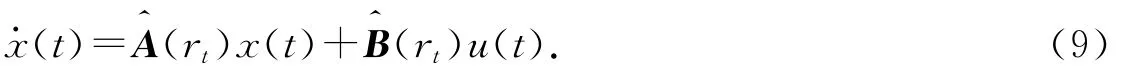
由穩定性條件和系統模型可知，控制器模型為u（t）＝Kix（t）.

由Lyapunov穩定性條件，設能量方程為V＝xTPix，對能量方程進行弱微分，可得

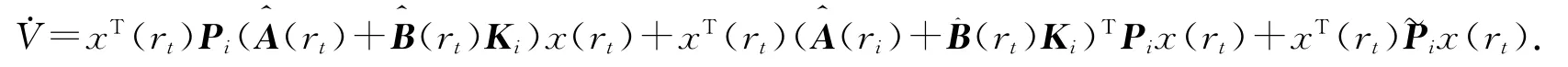
將上式中的確定因素和不確定因素分開得到

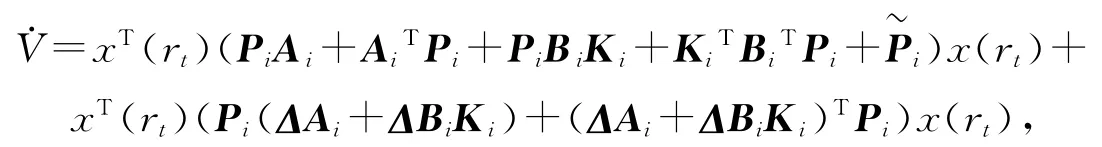
其中，為了書寫方便，使用Ai，Bi，ΔAi，ΔBi代替A（rt），B（rt），ΔA（rt），ΔB（rt）.結合式（2），上式中的不確定因素可寫為，根據定理2，可知D＝PiEi，E＝［F1iF2iKi］.

要求證Q＋DF（t）E＋（DF（t）E）T＜0，即求證存在參數εi＞0使得，即

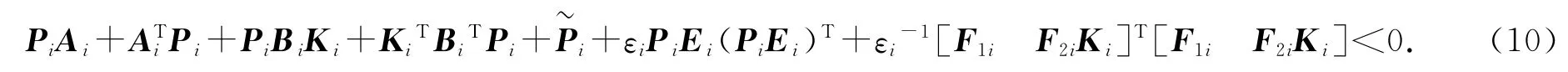
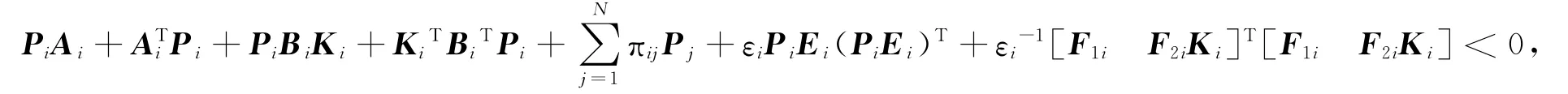
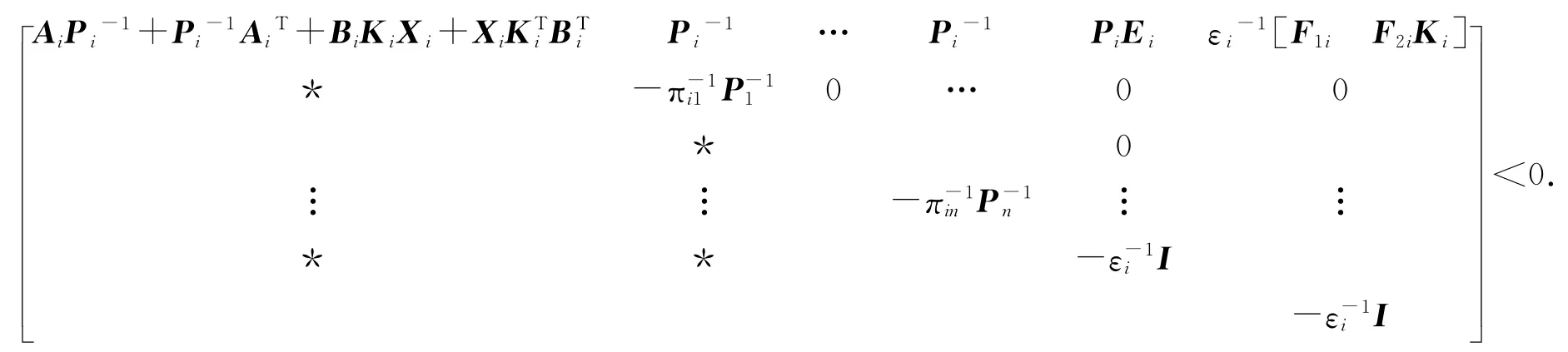
令Yi＝KiXi，得

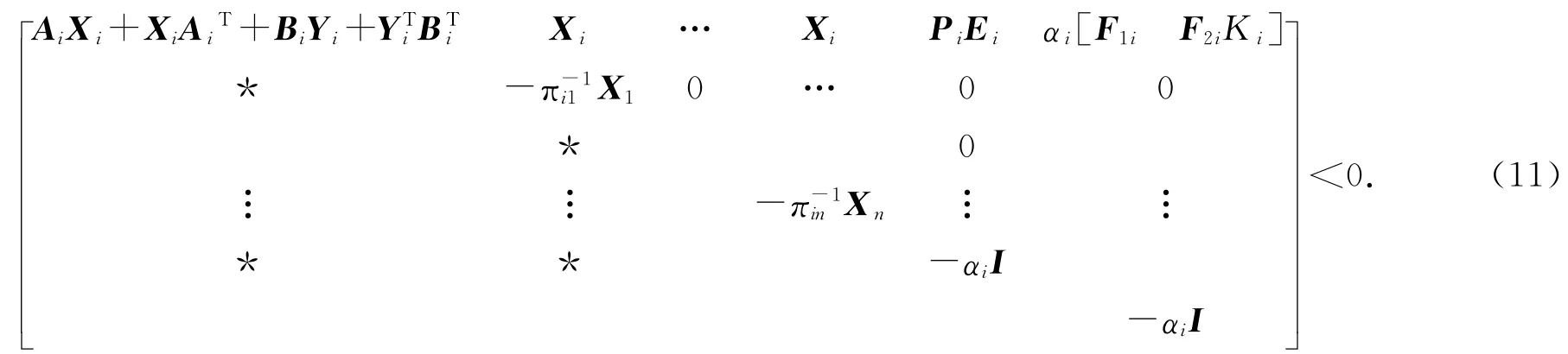
由上式可知，式（11）即為系統魯棒穩定性條件，可根據式（11）進行控制器形式的求取.其中，在實際仿真中，一般忽略系統輸入的不確定影響即使ΔB＝0，即輸入變量中的不確定因素為0，所以上式F2i＝0，得到如下矩陣不等式：

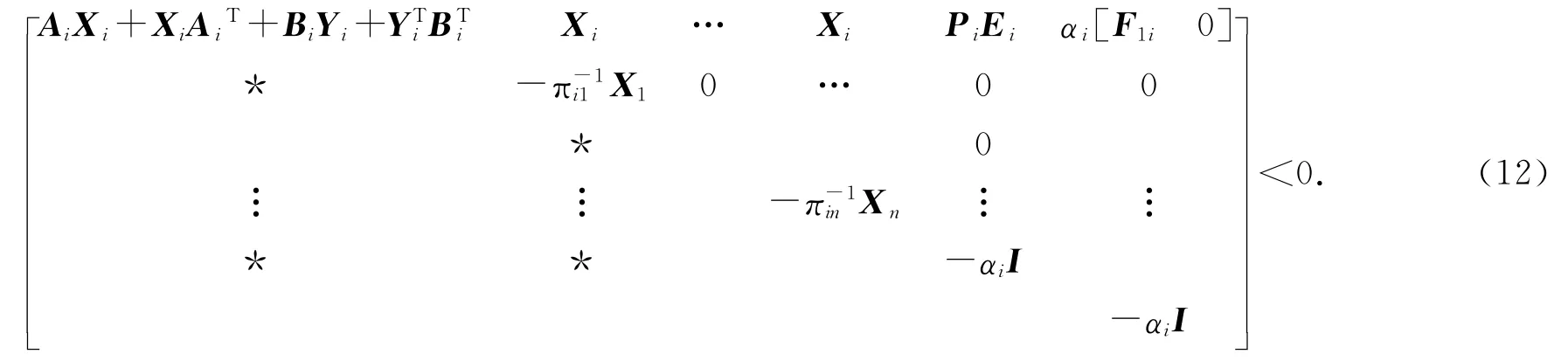
式（12）即為忽略輸入量不確定性的魯棒穩定性條件，在進行仿真實驗時即選取式（12）進行仿真.

3 數值算例

由式（12）可知控制器的LMIs形式，已知系統1與系統2以及不確定因素如下：

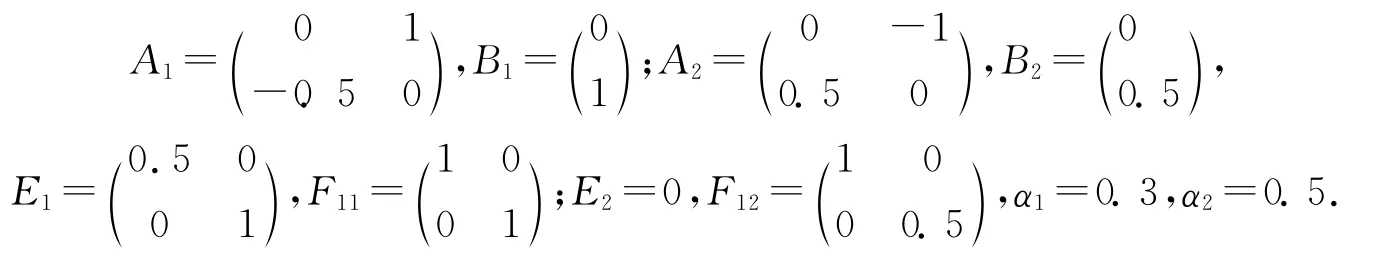
通過LMIs仿真得到

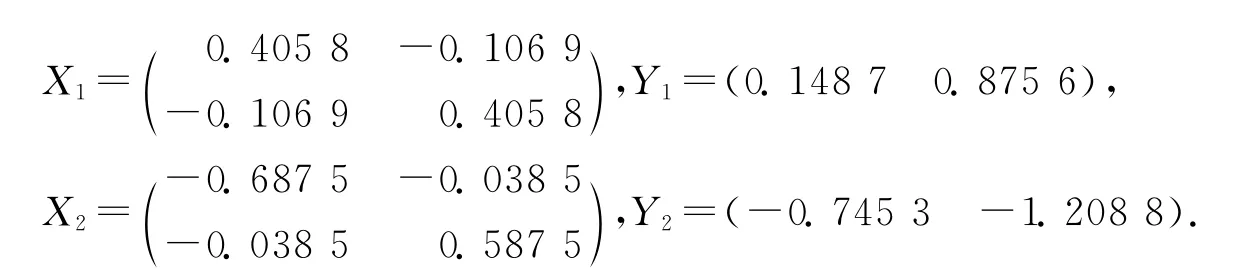
可得到控制器結果為K1＝［1.238 7 1.448 0］；K2＝［0.759 8 2.145 5］；t＝－0.423 56.

由結果可知，使用該方法可得到簡單不確定系統的魯棒控制器參數，且t值在單位圓的負平面，說明其能量呈現衰減的趨勢，系統最終控制在穩定的狀態，因此，可知該控制器可對不確定系統進行控制.

4 結束語

針對帶有Markovian參數的不確定性系統，通過Lyapunov穩定性原理以及線性矩陣不等式中的Schur補原理以及范數有界矩陣消除法對系統的穩定性條件進行推導及證明，進行了穩定性分析和魯棒穩定控制器的設計，得到了系統的魯棒穩定性條件和控制器形式，并通過對LMIs方法的綜合運用，進行了一系列仿真，得到了數值算例的穩定性條件和控制器參數，實現了對系統的不確定參數造成的隨機性進行控制，保證了不確定性系統的穩定性.

［1］ 關永強.參數不確定性系統的魯棒穩定性研究［D］.湘潭：湘潭大學，2010.

［2］ 王曰英，周平方，陳麗，等.馬爾可夫跳躍系統的魯棒故障檢測［J］.電力自動化設備，2010，30（5）：83－84.WANG Yueying，ZHOU Pingfang，CHEN Li，et al.Robust fault detection of Markovian system［J］.Electric Power Automation Equipment，2010，30（5）：83－84.

［3］ MAHMOUD M S，SHI Ping.Robust stability，stabilization and H－∞control of time－delay systems with Markovian jump parameters［J］.Robust Nonlinear Control，2003，13（3）：755－784

［4］ 俞力.魯棒控制－線性矩陣不等式處理方法［M］.北京：清華大學出版社，2002.

［5］ 丁強，鐘麥英.一類線性Markov跳躍區間時滯系統的魯棒H－∞故障檢測濾波器設計［J］.控制與決策，2011，26（5）：712－715. DING Qiang，ZHONG Maiying.Design of robust H－∞fault detection filter for a class of linear Markovian jump systems with interval time－delay［J］.Control and decision，2011，26（5）：712－715.

［6］ 姚秀明.混雜Markovian 跳躍系統的分析與綜合［D］.哈爾濱：哈爾濱工業大學，2010.

［7］ XIE Lihua.Output feedback H－∞control of systems with parameter uncertainty［J］.Int J Control，1996，63（4）：741－751.

［8］ 葉思雋，王新民，張清江，等.不確定系統混合H2／H∞魯棒控制的直接迭代LMI方法［J］.控制理論與應用，2011，28（2）：248－251.YE Sijun，WANG Xinmin，ZHANG Qingjiang，et al.Direct iterative LMI－based approach of mixed H－two／H－infinity robust control for uncertain systems［J］.Control Theory and Application，2011，28（2）：248－251.