小球能一直沿光滑曲面運動下去嗎？

陳 科

（甘肅省康縣第一中學(xué)，甘肅 康縣 746500）

初速度為0的小球能沿任意光滑斜面一直運動下去，這是眾多高中生都熟悉的.那么，初速度為0的小球沿光滑曲面也能一直運動下去嗎？本文將分3種情況：圓面、拋物面和橢圓面，就這一問題做一探討，供各位同行參考.

1 光滑圓面情況

設(shè)小球?qū)⒃贏點脫離圓面，如圖1所示.

圓的方程為

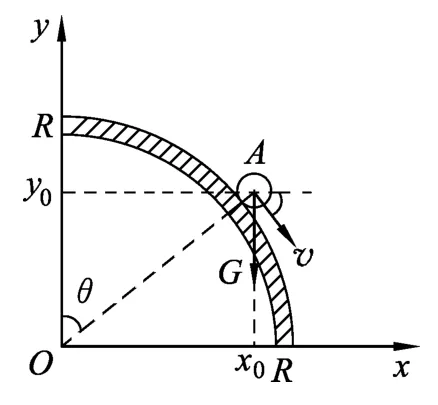
圖1 光滑圓面

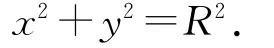
參數(shù)方程為

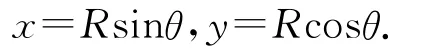
從最高點到A點機械能守恒，有

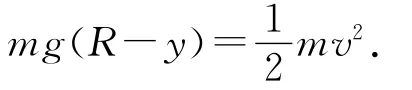
在A點的脫離條件為

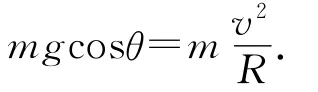
由以上各式，解得

故初速度為0的小球不可能一直沿光滑圓面運動下去，且將在θ＝48°處脫離圓面.

2 光滑拋物面情況

設(shè)小球?qū)⒃贏點脫離拋物面，如圖2所示.

拋物線的方程為

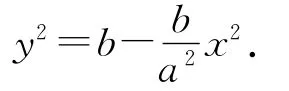
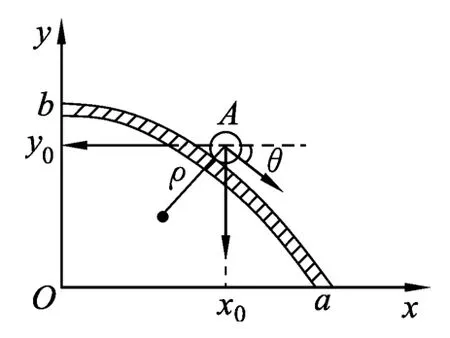
圖2 光滑拋物面

對y關(guān)于x求一階、二階導(dǎo)數(shù)，得

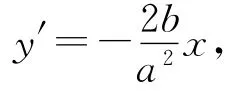
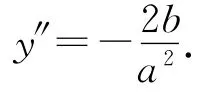
A點曲率半徑為

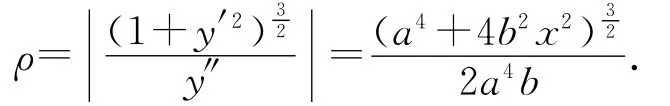
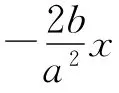
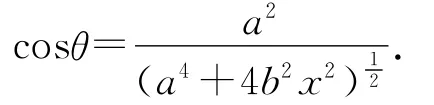
從最高點到A點機械能守恒，有

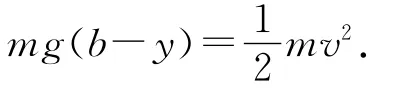
在A點的脫離條件為

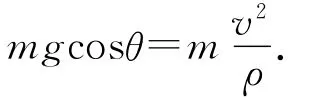
由以上各式，解得

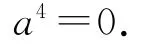
方程兩邊含x的項剛好抵消，方程無解.

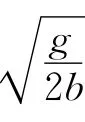
3 光滑橢圓面情況

設(shè)小球?qū)⒃贏點脫離橢圓面，如圖3所示.

橢圓的方程為

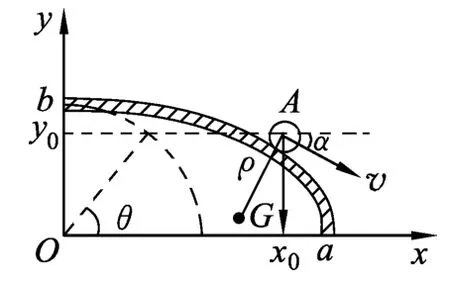
圖3 光滑橢圓面

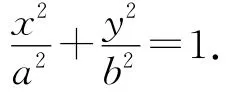
參數(shù)方程為

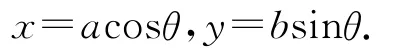
分別對x與y關(guān)于θ求一階、二階導(dǎo)數(shù)，得

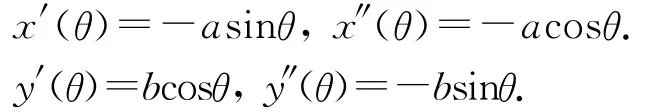
那么，y關(guān)于x的一階導(dǎo)數(shù)為

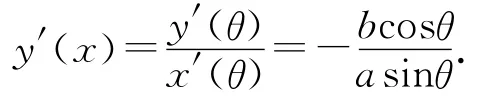
A點曲率半徑為

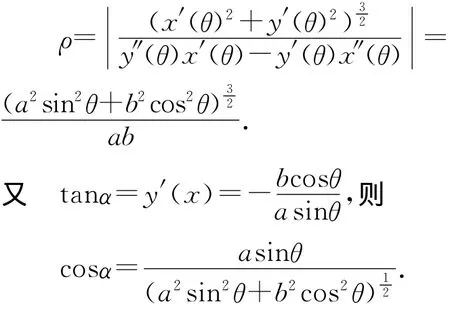
從最高點到A點機械能守恒，有

在A點的脫離條件為

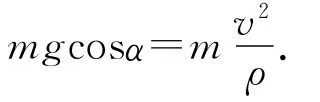
由以上各式，解得

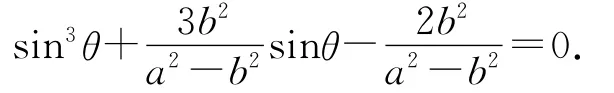
這是一個關(guān)于sinθ的一元三次方程.

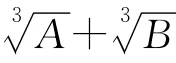
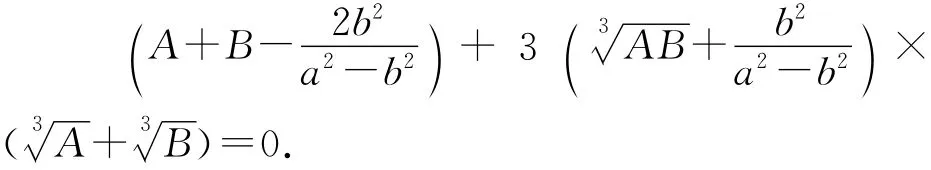
要使以上方程式成立，必須同時滿足

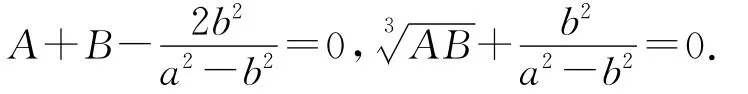
解上面關(guān)于A和B的方程組，得

即初速度為0的小球不可能一直沿光滑橢圓面運動下去，且將在以上確定位置脫離圓面.

最后，我們可以得出結(jié)論：初速度為0的小球?qū)⒁恢毖毓饣瑨佄锩孢\動下去；而在光滑圓面和光滑橢圓面上，該小球都將在某一確定位置脫離曲面.以上推導(dǎo)和觀點若有不當(dāng)之處，還望各位同行和專家斧正.