基于壓縮感知的圖像重構優化算法研究

李 爽（長春財經學院信息工程系,長春 130000）

基于壓縮感知的圖像重構優化算法研究

李 爽
（長春財經學院信息工程系,長春 130000）

摘 要：壓縮感知(Compressive Sensing，CS)理論知識于2006年正式提出，該理論知識利用信號數據的稀疏性或數據的可壓縮性加以實現信號數據的采集與編解碼。當信號數據有一定的稀疏性或者可壓縮性時，利用采集少量的投影值便可實現數據的近似重構。本文選用優化后的分段正交匹配追蹤 (StOMP) 算法為例，對壓縮感知圖像的重構算法進行了研究，并且在Matlab環境中采用不同采樣率，分別對Lena512國際標準測試圖像進行仿真實驗，并給出詳細的仿真實驗結果。

關鍵詞：壓縮感知；圖像重構；正交匹配追蹤(StOMP)

奈奎斯特(Nyqusit)采樣定理[1]要求在帶限數據采樣過程中，采樣率必須大于最高頻率的兩倍。在該理論指導下，數據信息的獲取、存儲、處理和傳輸等技術的實現即成為當今科學技術領域進一步向前邁步的重要技術瓶頸之一。具體來說，主要表現在如下兩個方面：（1）高采樣率的數據采集導致了較高成本。（2）在某些應用中[2-3]，奈奎斯特采樣定理支配的高采樣率導致了采樣樣本過多。顯而易見，這種基于奈奎斯特(Nyqusit)采樣定理為基礎的技術造成了大量資源的浪費。

2006年，由美國科學院院士D．Donoho、E．Candes同華裔科學家Τ．Τao等研究學者提出了一種全新的數據采樣理論——“壓縮感知”(Compressive Sensing，簡寫為“CS”)。該理論表明，當信號數據是可壓縮的，可以通過采取極少數量的信號投影值加以實現信號的近似重構，可以極大程度的降低了數據采集的成本。

1 測量矩陣的設定

在“CS”理論中，測量矩陣Ф的設定十分重要。Ф的合理性直接決定數據重構的質量，當測量數目達到臨界時，合理的測量矩陣就可以確保數據的準確恢復。

本文的研究選擇一個M×N的高斯矩陣作為測量矩陣，高斯測量矩陣的構造方式為設定矩陣Φ∈RM ×N，矩陣當中的每個數據元素都服從獨立分布，符合均值為0，方差為的高斯分布，即：

高斯測量矩陣的缺點是矩陣內元素所需存儲空間大，但優點在于它幾乎與任何稀疏信號都不相關，因而需要的測量次數最少。

2 壓縮感知算法的優化

本文對分段正交匹配追蹤 (StOMP) 算法進行二次優化，改善了原算法的部分缺陷，使其在計算時間上略有改進。

優化后的StOMP算法如下：

步驟1：初始化最大迭代步長maxstep，求解的最大迭代誤差e，s=1，然后求得迭代誤差的第一位非零數字記作n；

步驟2：對小波稀疏矩陣y 進行隨機測量，得：

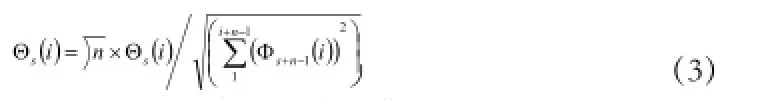
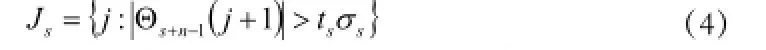
步驟5：結合一個最近子集，合并最新的兩次坐標索引，并對Is集合進行一致化處理，得Is：

步驟6：求解線性方程組：求得：

步驟7：計算殘差：

3 仿真實驗結果

仿真實驗采用Symmlet5為正交小波基做小波變換，采用國際標準測試圖像Lena.bmp作為測試圖像，對不同高頻子帶采用不同的采樣率，利用分段正交匹配追蹤(StOMP)算法對采樣后的圖像數據進行重構。分別求得峰值信噪比PSNR、圖像熵、灰度平均值，觀察實驗數據，比對算法的性能，得到仿真實驗結論。

在采樣率f1分別為0.1、0.05、0.01時，對Lena512x512圖像重構效果如下圖所示。

上圖StOMP算法對lena512圖像重構效果 (a)原始圖像 (b)f=0.1 (c) f=0.05 (d)f=0.01。

Lena512重構后圖像PSNR、圖像熵、灰度平均值的數據比對如下表所示。

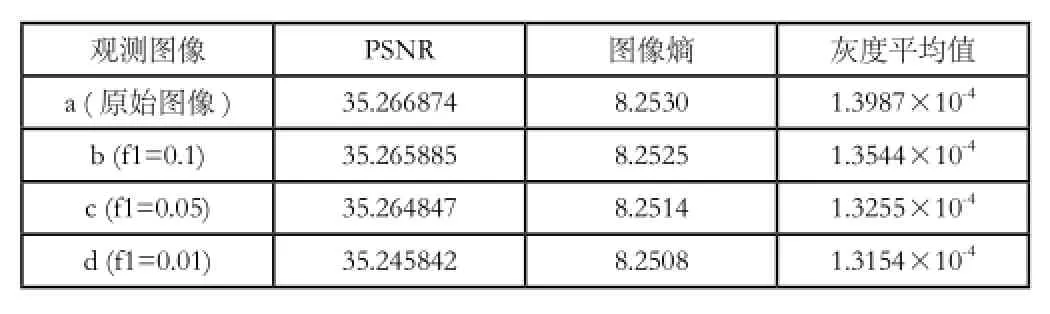
Lena512重構后圖像參數統計對比

4 結論

選用不同的采樣率，經優化后的StOMP算法重構后的圖像均保持較好，有著較好的視覺效果，隨著采樣率f的下降，PSNR值和圖像熵值逐漸減少，灰度平均值保持在一個數值上下，這表明我們可以用較少的采樣數據重構質量較好的圖像。

參考文獻：

[1]李曉陸.帶通采樣定理在降低功耗問題中的實際應用[J].桂林電子工業學院學報，2004,24(05):36-38.

[2]崔慶林，蔣和全.高速A/D轉換器動態參數的計算機輔助測試[J].微電子學，2004,34(05):505-509.

[3]王萍，石寅.一種用于高速A/D轉換器的高精度參考電壓電阻網絡[J].電子學報,2000,28(12):48-51.