基于帶寬-相位滯后準則的飛機PIO評估應用研究

王 磊（上海飛機設計研究院,上海 201210）

基于帶寬-相位滯后準則的飛機PIO評估應用研究

王 磊
（上海飛機設計研究院,上海 201210）

摘 要：現代飛機通常采用電傳控制律實現對飛機的三軸操縱，增穩功能和非線性環節的引入導致其易于出現駕駛員誘發振蕩，需要采用合適PIO評價準則預期閉環飛機的PIO趨勢，以更好地指導控制律設計。本文對帶寬-相位滯后準則輔以修訂回落量準則的評估方法開展研究，并以算例飛機為對象進行評估應用研究。研究結果表明，這一評估方法可以較好地預測閉環飛機的PIO趨勢。

關鍵詞：飛機；控制律；駕駛員誘發振蕩；帶寬；相位

0 引言

駕駛員誘發振蕩（Pilot Induced Oscillations，PIO）屬于不利的人機耦合振蕩，當駕駛員操縱飛機時有時會出現持續或不可控的飛機響應振蕩。由于PIO會極大地降低飛機的飛行品質甚至影響其飛行安全，因此需要在飛機設計初期開展PIO趨勢的預測評估，以更好地指導飛機的總體設計、飛行品質評估和控制律設計等。按照PIO的振型分類，通常可分為3類PIO，I類PIO屬于線性人機耦合振蕩，主要是由于系統相位滯后或時延過大而產生[1]。

電傳飛機采用了具有控制增穩功能的飛行控制系統，閉環系統中涉及到很多的高增益和非線性環節等，這些因素可能會導致整個閉環高階系統的相位滯后和時延增大等，進而影響其產生PIO的趨勢。

本文采用帶寬-相位滯后準則開展I類PIO評估，并將其應用于某電傳飛機上，以探討這一評估方法的使用，研究結果可用于飛機的PIO評估時使用，并用于指導飛機的控制律設計。

1 研究對象

本文的評估基于帶控制律的閉環算例飛機的俯仰角和俯仰角速度的短周期低階等效模型：

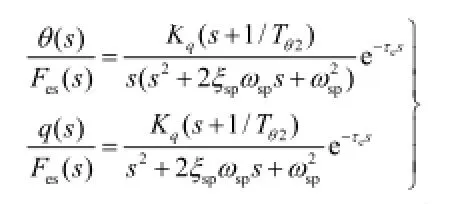
式中：Τθ2為等效短周期的分子時間常數，sp和sp分別為等效短周期的阻尼比和自然頻率，e為等效時間延遲。

實際上，由于短周期低階等效擬配的考察頻率范圍在0.1～10rad/ s[1. 2]（為了避免長周期的影響，左邊界往往會右移），而頻域PIO準則的評價通常也在這一頻率范圍內，因此閉環高階和低階等效系統在高頻段的頻響類型也是非常接近的，故采用低階等效系統的頻響特性來考察帶寬-相位滯后準則是適合的。

針對算例飛機在不同重量、前或后重心位置和不同飛行狀態下，開展I類PIO趨勢評估，可預測該型飛機的I類PIO趨勢，并可用于指導該飛機的控制律設計。

2 帶寬-相位滯后準則定義與評估方法

帶寬-相位滯后準則重點從考察飛機的開環俯仰姿態頻響特性的角度出發。該準則由規定的開環系統的帶寬ωBW及相位滯后τp的相互關系而確定。帶寬ωBW 的確定基于飛機的開環俯仰姿態頻域響應圖，取相位裕度等于45°或幅值裕度等于6dB所對應頻率的較小者[2]，如所圖 1示。相位滯后τp的確定如下式所示[1, 2]：

式中：ω180是相位等于?180°時的頻率；是2倍ω180頻率處的相角。從物理意義上來說，相位滯后τp可以看成是高增穩飛機的一個等效相位滯后。

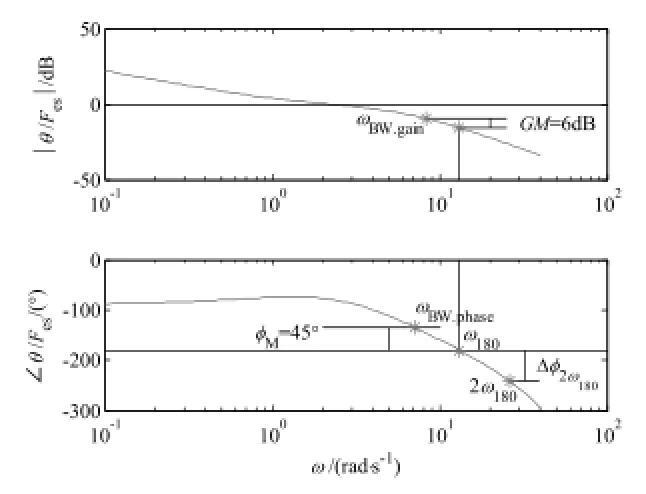
圖 1 開環俯仰姿態頻率響應伯德圖

依上述定義，給出帶寬ωBW和相位滯后τp的具體求解方法如下：

（1）求得系統開環俯仰姿態頻域響應的伯德圖（見圖 1）；

（2）從相頻特性曲線上確定相角等于?180°的頻率ω180，然后找到相位裕度為45°，即相角等于?135°的頻率ω135，該頻率定義為相位帶寬；然后找到與ω180所對應的幅值，在此基礎上增加6dB，從而求得幅值帶寬。帶寬ωBW取為與中的較小者；

實際上，帶寬ωBW是能閉合飛機-駕駛員回路而又不危及閉環系統穩定性的最高頻率參數[1]。它是一種頻率度量，在該頻率以下，飛機能夠跟隨所有的駕駛員指令；在該頻率以上則無法完全跟隨。另外，從相位滯后τp的確定可見，它是?180°附近相頻曲線斜率的一種度量。

帶寬-相位滯后準則能夠較為有效地預示PIO趨勢，特別是能很好地預測高頻相位跌落造成的PIO。該準則的判據如圖 2（a）所示，要求如下[3]：

（1）如果在起飛階段相位滯后τp≥0.12s，著陸階段τp≥0.15s，則飛機有PIO的趨勢；

（2）如果回落量過大且帶寬ωBW≤2rad/s，則飛機有PIO的可能性；

（3）如果帶寬ωBW≥2rad/s且相位滯后τp≤0.12s，則過大的回落量將導致飛機產生“點頭”現象，但是不會產生嚴重的PIO。

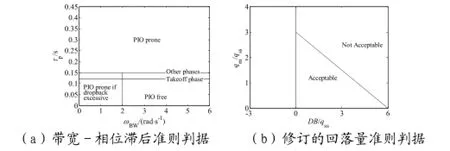
圖 2 帶寬-相位滯后準則判據和修訂的回落量準則判據

當飛機落入“有PIO的可能性”區域，還需通過其回落量來判斷其是否具有“確定的PIO趨勢”。文獻[1, 2]指出：（1）在飛行航跡控制和跟蹤時，負的姿態回落（即姿態超調）將導致緩和不可預測的響應，有時會伴隨嚴重的PIO；（2）在跟蹤任務中，增加姿態回落（具有較大的俯仰速率超調）將會導致突變響應和“點頭”，從“輕微趨勢”到“持續振蕩”，有時又稱為PIO。這表明，負的姿態回落和過大的回落量都是不滿意的，它們都容易導致飛機出現PIO趨勢。

采用修訂的回落量準則，準則判據如圖 2（b）所示。

3 評估應用

按照上述求解方法，求得算例飛機的俯仰姿態-桿力開環頻響的帶寬ωBW和相位滯后τp。帶寬-相位滯后準則的評估結果如圖 3所示。

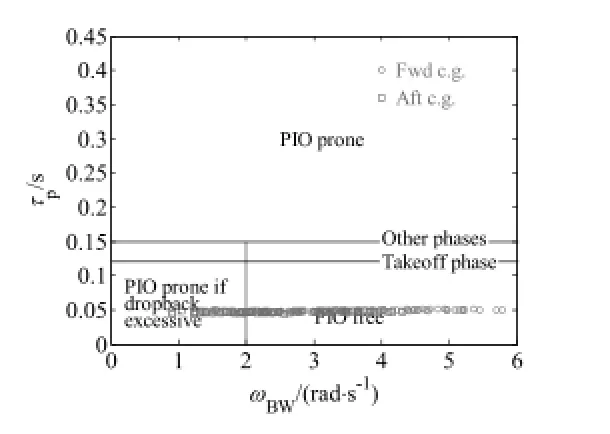
圖 3 帶寬-相位滯后準則評估結果圖

從圖 3可以看出，算例飛機的相位滯后τp均小于規定值；帶寬ωBW則覆蓋了較大的頻率區域，從0.8rad/s到6rad/s。另外，通過對比計算結果的原始數據可知，低階等效系統的短周期自然頻率sp很接近于帶寬ωBW，正因如此，算例飛機在控制律提供相同增穩條件下后重心時較小的自然頻率使得其帶寬ωBW也相對較小。

從圖 3可以看出，一部分狀態點確定不具有PIO的趨勢；而另一部分的狀態點具有可能的PIO趨勢，還需通過判斷其回落量是否過大或為負值來進一步確定其PIO趨勢。

下面通過修訂的回落量準則來考察其回落量，評估結果如圖 4所示。

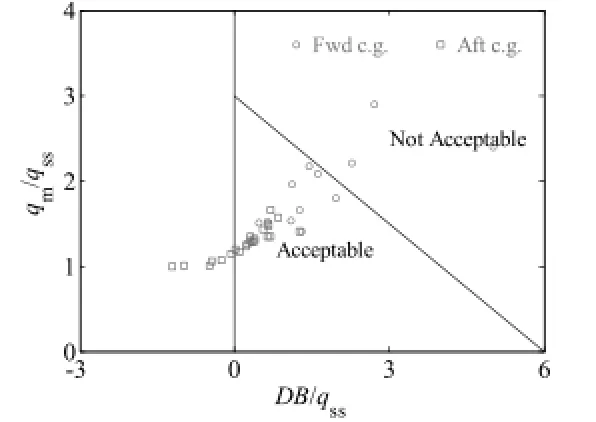
圖 4 修訂回落量準則評估結果圖

從圖 4可以看出，算例飛機在前重心情況下傾向于往右上邊界跑，部分出現回落量過大的情況；而在后重心情況下則傾向于往左邊界跑，部分出現回落量為負的情況。原始計算數據還表明，負的回落量DB/ qss往往對應于后重心、過阻尼的情況，即低階等效系統的短周期阻尼比sp＞1。

經修訂回落量準則下的進一步評估，確定算例飛機的PIO評估結果：考察的狀態點中，有6%的狀態點具有PIO趨勢。

4 結論

通過以上的研究，可以得出以下結論：

通過采用帶寬-相位滯后準則可以預測飛機可能存在的PIO趨勢的狀態點，然后輔以修訂回落量準則進一步確定具有PIO趨勢的狀態點。

參考文獻：

[1]高金源. 飛機飛行品質[M]. 國防工業出版社, 2003.

[2]MIL-HDBK-1797, Flying qualities of piloted aircraft[S]. 1997.

[3]RTO-TR-029, Flight control design - best practices [R]. 2000.