一類具有時滯垂直傳播的HIV/AIDS模型的穩定分析

祖克熱古麗·吾斯曼，夏米西努爾·阿布都熱合曼

(新疆大學數學與系統科學學院，烏魯木齊 830046)

艾滋病的醫學全名為“獲得性免疫缺陷綜合征”(英文縮寫AIDS)，是由艾滋病病毒(人類免疫缺陷病毒－HIV)引起的一種嚴重傳染病。艾滋病病毒侵入人體后會破壞人體的免疫功能，使人體發生多種難以治愈的感染和腫瘤，最終導致死亡。艾滋病病毒對外界環境的抵抗力較弱，離開人體后，常溫下只能生存數小時至數天。高溫、干燥以及常用消毒藥品都可以殺滅這種病毒。據專家介紹，艾滋病病毒感染者從感染初期算起，要經過數年、甚至長達10年或更長的潛伏期后才會發展成艾滋病病人。艾滋病病人因抵抗能力極度下降會出現多種感染，如帶狀皰疹，口腔霉菌感染，肺結核，特殊病原微生物引起的腸炎、肺炎、腦炎，念珠菌、肺囊蟲等多種病原體引起的嚴重感染等，后期常常發生惡性腫瘤，直至因長期消耗導致全身衰竭而死亡。隨著人類對艾滋病認識的加深，越來越多的人開始研究艾滋病，數學家們也不例外。

艾滋病傳播方式主要有3種，其中垂直傳播(母嬰傳播)是主要傳播形式。文獻［1－4］研究了艾滋病垂直傳播模型并得到相應的結果。事實上，加時滯的垂直傳播模型更接近于實際。因此，本文研究加時滯垂直傳播模型。

本文討論了一類帶有時滯垂直傳播的HIV/AIDS傳播模型，給出了2個平衡點。研究了當R0＜1時無病平衡點全局漸進穩定和地方病平衡點時滯等于零時的全局穩定性。第1部分給出了模型;第2部分證明了解的正性，找出了解集;第3部分求出平衡點和基本再生數;第4部分討論無病平衡點的穩定性;第5部分研究地方病平衡點的穩定性。

1 模型的建立

本節對 Swarnali Sharma［5］的垂直傳播模型增加時滯考慮，建立了一類具有時滯垂直傳播的HIV模型，根據條件考慮了模型的2個平衡點的穩定性。當基本再生數小于1時，研究了無病平衡的全局漸進穩定性和地方病平衡點的局部穩定性。

研究中把高危人群分為5種類型:易感者S(t);有癥狀的感染者I1(t);無癥狀的感染者I2(t);在接受治療的感染者T(t);艾滋病患者A(t)。

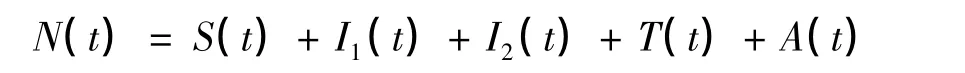
這里，假設易感者和感染者為同性戀且發生率為雙線性。根據以上假設得到數學模型為:

式中:Λ是易感者的輸入率;β1是易感者和無癥狀的感染者接觸時的平行傳播發生率;β2是易感者和有癥狀的感染者接觸時的平行傳播發生率;η是垂直傳播率，即新出生的感染的嬰兒進入無癥狀階段的比例;α是無癥狀的人群發展到有癥狀的階段的比例;ρ是有癥狀的人群進入接受治療的感染者人群的比例;σ是有癥狀的人群直接進入艾滋病患者的比例;γ是接受治療的人群進入艾滋病患者的比例;d是艾滋病患者的因病死亡率;μ是自然死亡率。

模型(1)的初始條件為:S(θ)=φ1(θ)，I1(θ)=φ2(θ)，I2(θ)=φ3(θ)，T(θ)=φ4(θ)，A(θ)=φ5(θ)，且 φi(θ)≥0，i=1，2，3，4，5，對任意 θ∈［－ τ，0］。由生物意義還可得到 φi＞0，i=1，2。

2 解的正性及解集

定理1 對任意t≥0，在初值條件下，模型(1)的所有解為正解，且所有解進入集合:

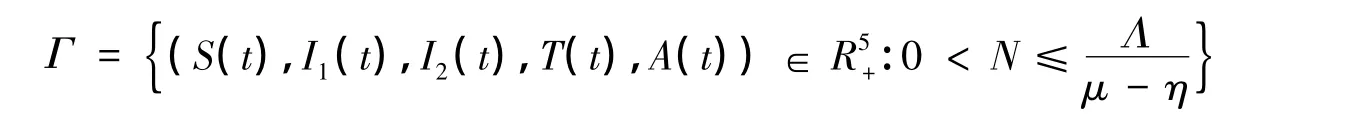
證明 解的正性顯然，省略。下面證有界性。

模型(1)的5個方程相加得

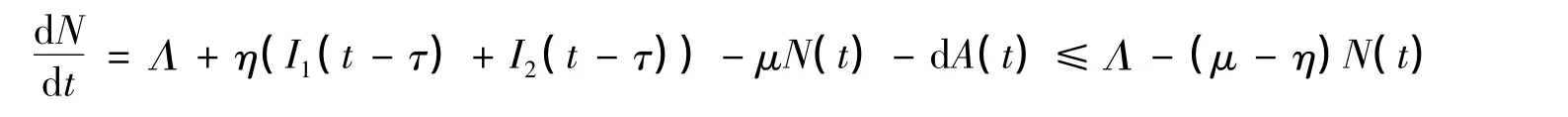
以下討論始終假設μ＞η。綜上可得定理1的結論。

3 平衡點和基本再生數

模型(1)的前3個方程不包含T(t)和A(t)，因此以下只討論三維的情形:

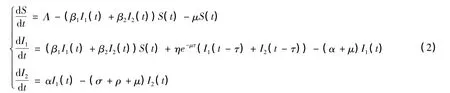
顯然，如果R0＞1，則模型(2)存在一個正的地方病平衡點E*=(S*，)，且:

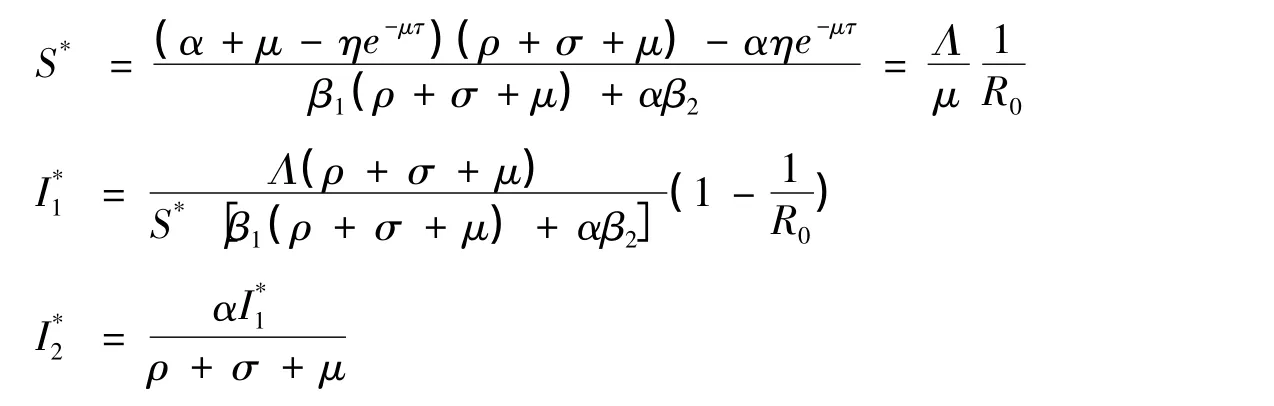
4 無病平衡點的穩定性

定理2 如果R0＜1，那么模型(2)的無病平衡點E0在Γ內局部漸近穩定。

證明 模型(2)在E0處的雅克比矩陣的特征方程為:

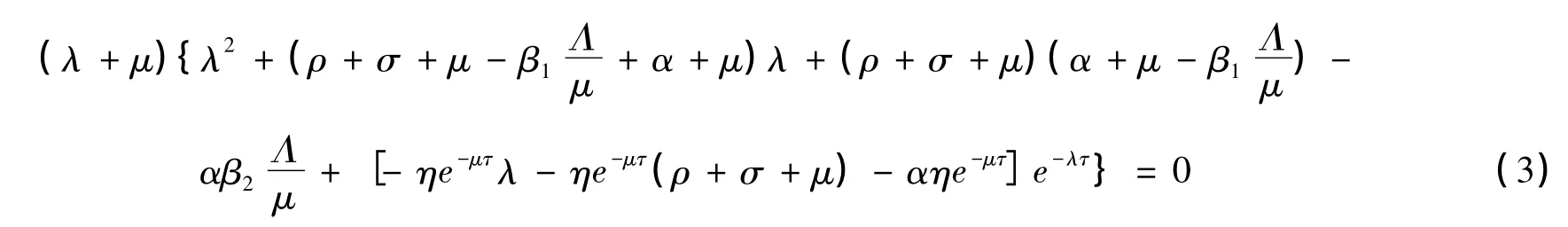
顯然一個特正根為λ=－μ。因此，只需討論如下方程:

當τ=0時，方程(4)可寫成:

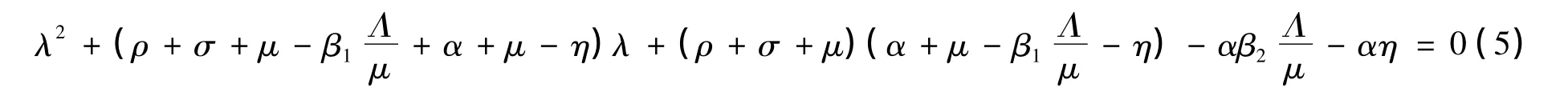
式(5)中令λ的系數為C1，常數項為C2，則由R0＜1可得

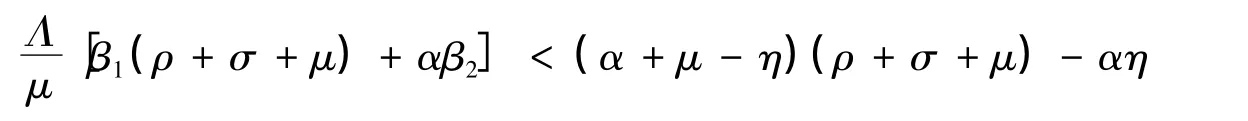
由此可得C2＞0。由

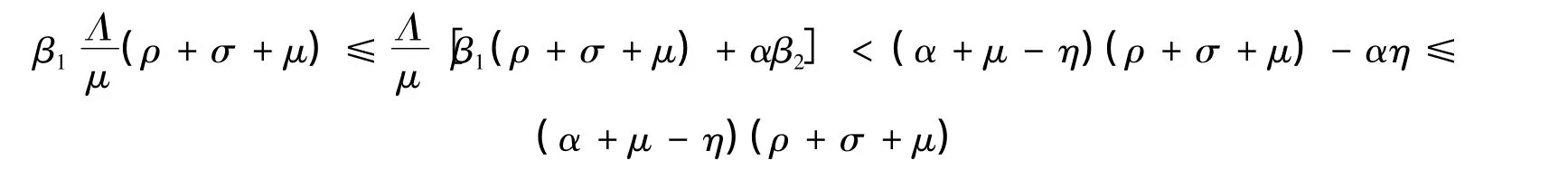
由Hurwitz判據［6］可得:當τ=0時，E0局部漸近穩定。

如果τ＞0，假設(4)存在λ=iω(ω＞0)形式的根，則ω應滿足等式

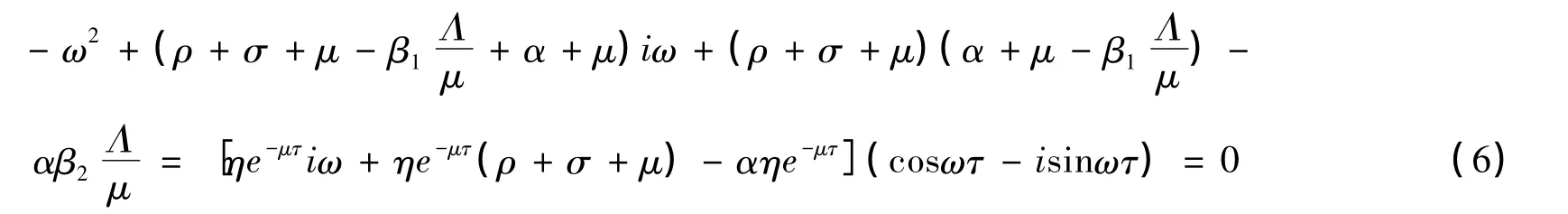
分離實部和虛部得

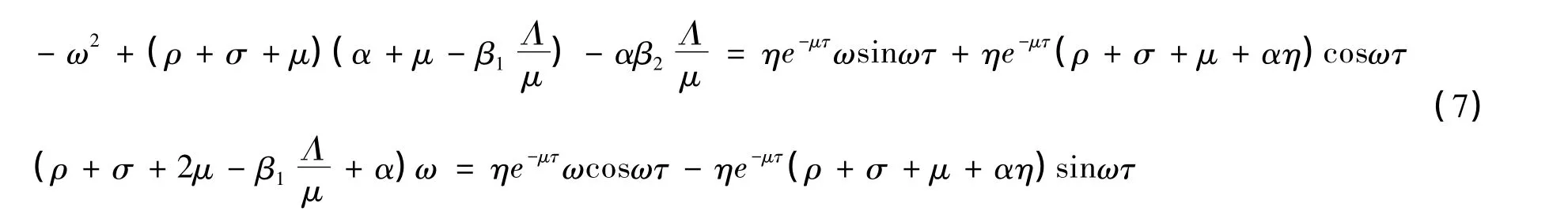
將式(7)的2個方程平方相加得

其中

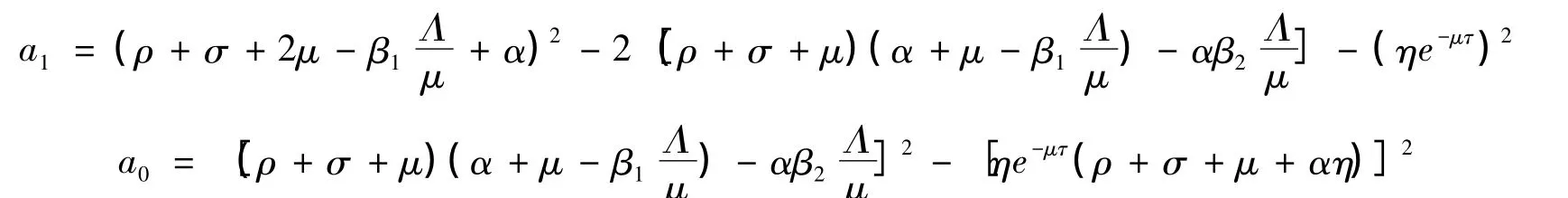
當R0＜1時可得a1＞0，R0＜1意味著

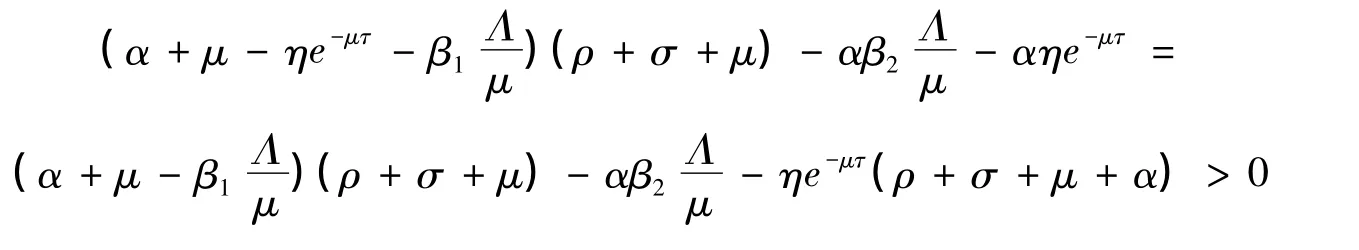
這說明

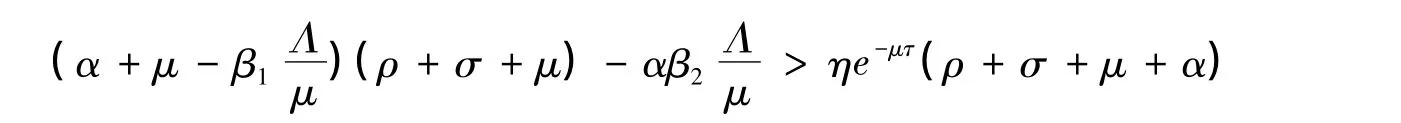
兩邊平方后左邊剛好是a0，因此方程(8)無正根。這說明方程(4)沒有λ=iω形式的根，故其所有根具有負實部。由時滯微分方程一般理論［7－10］知:當R0＜1時，模型(2)的無病平衡點E0是局部漸近穩定的。

下面證明無病平衡點的全局漸進穩定性。

定理3 如果R0＜1，那么模型(2)的無病平衡點E0在Γ內全局漸近穩定。

證明 構造Lyapunov函數如下:

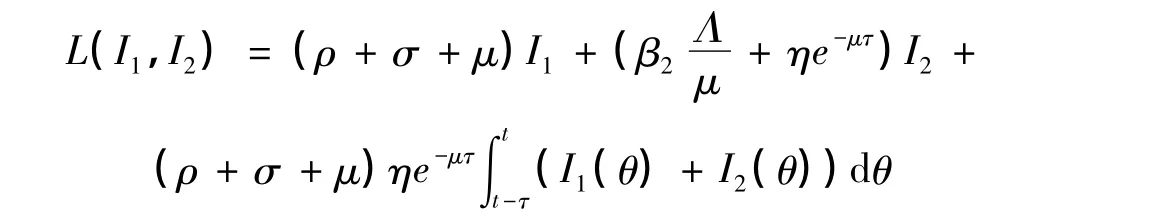
對L沿著模型(2)求導數得

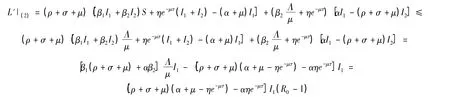
當 R0＜1 時，L'|(2)≤0，等式 L'|(2)=0，當且僅當 I1=0 時成立。因此，集合{(S，I1，I2):L'|(2)=0}的最大不變集為單點集{E0}。由LaSalle不變形原理［5］知:無病平衡點E0在Γ內全局漸近穩定。

5 地方病平衡點的穩定性

本節對τ=0時的模型進行討論。當τ=0時在文獻［5］中已證明了地方病平衡點的局部漸近穩定性。下面用Lyapunov函數的方法證明地方病平衡點的全局漸進穩定性。

定理4 如果R0＞1，那么模型(2)的地方病平衡點E*在Γ內全局漸近穩定。

證明 構造的Lyapunov函數如下，

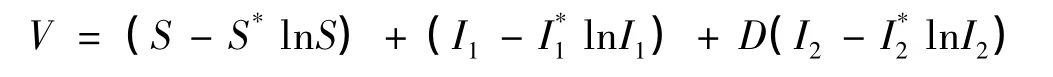
其中D是待定常數。對V沿模型(2)求導得

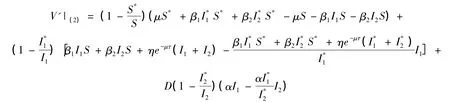
下面進行變量替換，令

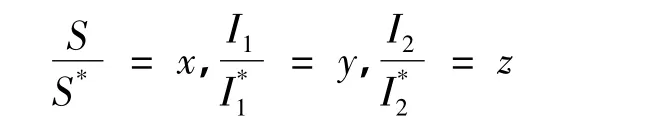
整理可得

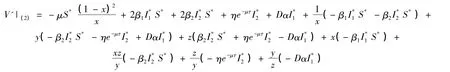
D定義為

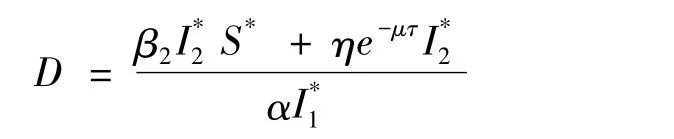
則有

由算數平均數大于或等于幾何平均數可得

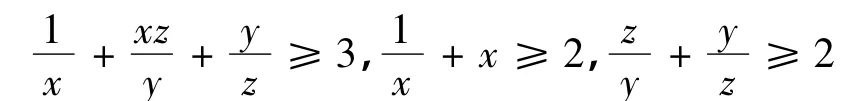
因此，在Γ內有V'|(2)≤0，等式當且僅當x=y=z=1時成立，即S=S*，I1=，I2=。模型(2)集合{(S，I1，I2):V'|(2)=0}上的最大不變集為單點集{E*}。由 LaSalle不變原理［8］知:當 R0＞1時，模型(2)的地方病平衡點E*在Γ內全局漸近穩定。

6 數值仿真

下面通過數值仿真來說明本文結論的正確性和方法的有效性。數值仿真采用Matlab軟件。表1和2中的一些參數取自相關文獻［5］，另外一些參數由估計所得。

圖1、2說明:對于不同的初始值，兩類平衡點都是全局漸近穩定的。

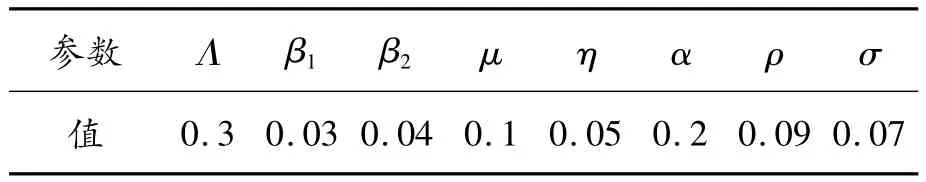
表1 仿真參數1

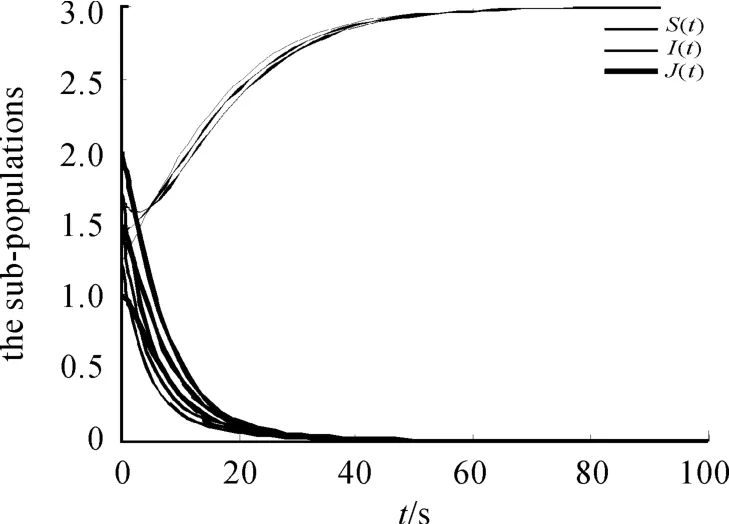
圖1 R0=0.607 7

表2 仿真參數2

圖2 R0=3.698 3

7 結束語

本文研究了一類帶時滯垂直傳播的HIV/AIDS傳播模型的穩定性。微分方程的性態由基本再生數控制。若R0＜1，則無病平衡點全局漸近穩定;當R0＞1且τ=0時，得到了地方病平衡點的全局穩定性;當τ＞0時，通過數值模擬可得地方病平衡點是全局漸近穩定的。其理論證明有待進一步研究。

［1］Naresh R，Sharma D.An HIV/AIDS model with vertical transmission and time delay［J］.World Journal of Modeling and Simulation，2011(7):230 －240.

［2］Naresh R，Tripathi A，Omar S.Modelling the spread of AIDS epidemic with vertical transmission［J］.Applied Mathematics and Computation，2006，178:262 －272.

［3］Liming Cai，Xuezhi Li.Stability analysis of an HIV/AIDS epidemic model with treatment［J］.Journal of Computational and Applied Mathematics，2009，229:313 －323.

［4］Elaiw A M.Global properties of a class of HIV models［M］.Nonlinear Analysis:Real World Applications，2010:2253 －2263.

［5］Swarnali G P.Dynamical Behaviour of an HIV/AIDS Epidemic Model［J］.Differential Equation Dynamic Systems，2014，22(4):369－395.

［6］馬知恩，周義倉，王穩地.傳染病動力學的數學建模與研究［M］.北京:科學出版社，2004.

［7］Kuang Y.Delay Differential Equations with Applications in Population Dynamics［M］.New York:Academic Press，1993.

［8］LaSalle J P.The Stability of Dynamical Systems，in:Regional Conference Series in Applied Mathematics［M］.Philadelphia:SIAM(Society for Industrial and Applied Mathematics)，1976.

［9］Dongmei Xiao，Shigui Ruan.Global analysis of an epidemic model with nonmonotone incidence rate［J］.Mathematical Biosciences，2007，208:419 －429.

［10］Hai-Feng Huo，Li-Xiang Feng.Global stability for an HIV/AIDS epidemic model with different latent stages and treatment［J］.Applied Mathematical Modeling，2013，37:1480 －1489.