基于改進單相dq變換與形態濾波的電壓暫降檢測方法

金顯吉， 佟為明， 盧雷， 李鳳閣

(哈爾濱工業大學電氣工程及自動化學院，黑龍江哈爾濱150001)

基于改進單相dq變換與形態濾波的電壓暫降檢測方法

金顯吉， 佟為明， 盧雷， 李鳳閣

(哈爾濱工業大學電氣工程及自動化學院，黑龍江哈爾濱150001)

針對電壓暫降特征量檢測時存在的實時性差、準確度低的問題，結合數學形態學理論和d-q變換原理提出了一種基于改進單相d-q變換與形態濾波的電壓暫降檢測方法。研究了改進單相d-q變換算法實現原理，構造了混合形態濾波器，并給出了濾波器結構參數選擇依據。仿真分析了方法在理想電壓暫降波形和含諧波電壓暫降波形下的檢測性能，并進行了實驗驗證。仿真分析和實驗驗證結果表明運用改進單相d-q變換可以快速準確地得到暫降幅值和相位;形態濾波能夠去除檢測結果中非直流量，計算量小、精確度高。

電能質量;電壓暫降;形態濾波;dq變換;相位跳變

0 引 言

近年來，隨著現代工業及高科技產業的飛速發展，以計算機、微處理器為核心的設備得到了廣泛應用，它們對系統的擾動更敏感、對電能質量的要求更嚴苛。在各種電能質量問題中，電壓暫降對于敏感設備影響最為嚴重，是導致其故障機損壞的主要原因，會造成巨大經濟損失［1-3］。據統計，由電壓暫降造成的經濟損失占全部電能質量問題所造成的經濟損失的70%～90%［4］。電壓暫降不僅會造成經濟損失，還可能造成人員意外傷亡和設備毀壞。例如醫院的一些醫療保健設備、用計算機和微處理器控制的腦外科、心血管外科手術等，當發生電壓暫降而造成設備不能正常工作時將帶來嚴重后果［5］。因此對電壓暫降進行監測是十分必要的，而準確地檢測電壓暫降的特征量，如暫降深度、持續時間與相位跳變是電壓暫降監測的核心內容。

在電壓暫降的檢測方法中，較經典方法有:有效值法、缺損電壓法、電壓峰值法以及dq變換法等，也有學者將新的數學工具和信號處理方法如小波分析、傅里葉變換、神經網絡，Dyn測度、分形測度等應用于電壓暫降信號的檢測［6-11］。這些算法都有其自身的局限性，適用與不同的場合。例如，有效值法無法給出電壓暫降發生時可能出現的相位跳變，傅里葉變換法存在一個周波的延時，無法用于實時檢測中。目前較常用的方法是基于dq變換原理的方法，對于dq變換法，其最大優點就是檢測速度快，能夠瞬時檢測出暫降深度與相位跳變，且計算量小，但該算法受諧波畸變和噪聲的影響較大，而且只能用于三相對稱電壓暫降的檢測［12，13］。單相d-q變換法對傳統d-q變換算法進行了改進，使其適用于單相檢測，原理是根據單相電壓構造α-β靜止坐標系，再將α-β靜止坐標系變換到d-q旋轉坐標系，從而得到電壓暫降的特征量。該方法能夠適用于單相系統，但代價是增加了90。檢測延遲，動態響應較差。另外，在實際配電網系統中，系統電壓存在畸變和不平衡等問題，因此需要在d-q變換后的結果加低通濾波器，低通濾波器的時延特性給電壓跌落的實時檢測帶來了困難，為了選擇合適的低通濾波器，需要在濾波效果和時延兩方面進行綜合考慮。

本文提出的方法首先通過延時角度(理論上延時間角度可足夠小)構造虛擬三相系統，然后進行dq變換，并用dq分解法計算出電壓暫降深度和相位跳變，最后通過形態濾波器進行低通濾波，得到準確的基波電壓暫降深度和相位跳變信息。方法中延時角度的減小，使得檢測延時時間大幅減少，形態濾波器在電壓暫降檢測性能上也要優于傳統的低通濾波器，具有檢測計算量小、延時時間短、精度高等特點。改進單相d-q變換與數學形態濾波的結合提高了電壓暫降檢測是的實時性和精度。

1 改進單相d-q變換算法原理

利用理想三相電壓波形相同、相位相差120。的特點，依據磁場等效原理，在單相系統中構造虛擬三相電壓系統。

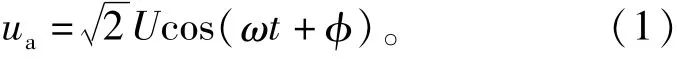
將ua延時60。，可以得到-uc，從而

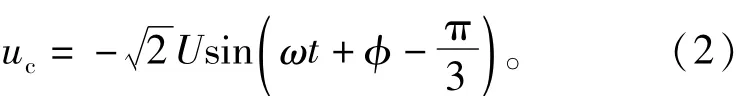
由于ua+ub+uc=0，因此

ua延時σ角度的電壓uσ為

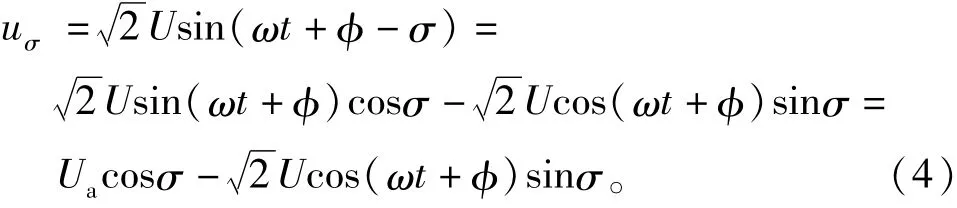
根據式(4)，可得

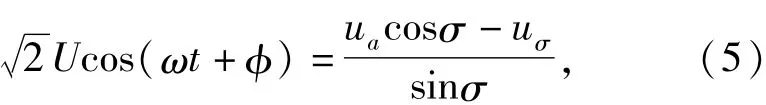
由式(2)和式(5)可得

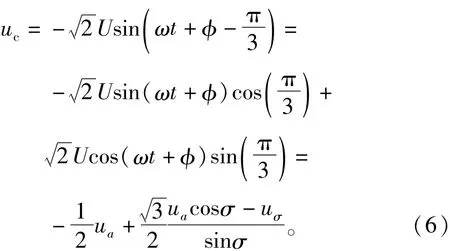
將式(6)代入式(3)可得

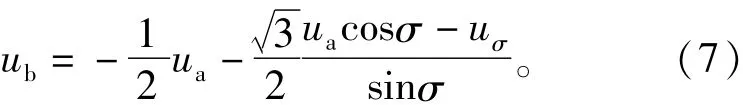
將三相電壓變換到d-q軸

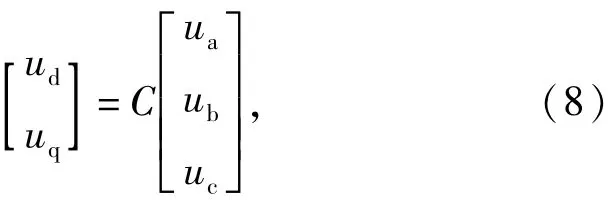
式中，

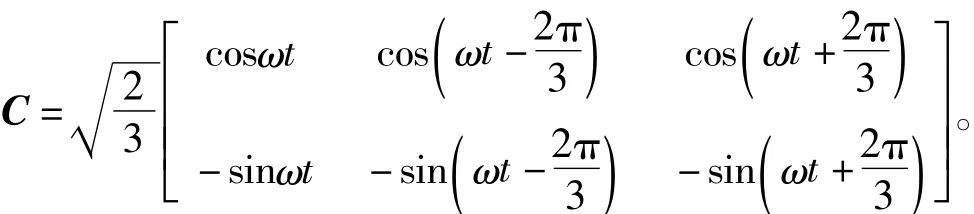
變換陣C中sinωt和cosωt是與a相電壓同相位的正、余弦信號。將式(6)和式(7)代入式(8)，計算后可得

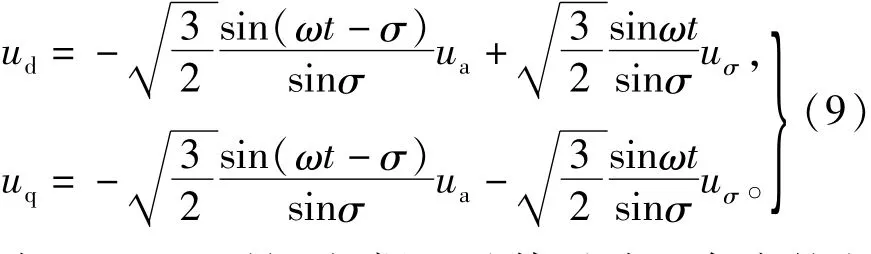
由于ua=u，所以根據u及其延時σ角度的電壓值uσ計算ud、uq有

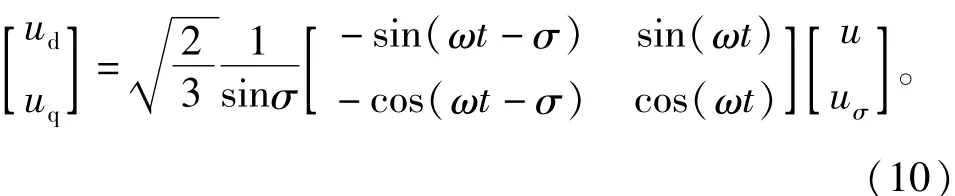
根據ud、uq即可求出單相電壓u的有效值與初始相位

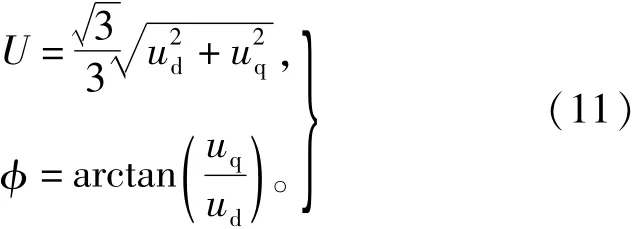
理論上，此改進算法所需的延時角度σ可以任意小，從而虛構信號與實際信號的延時可任意小，采用式(11)的檢測延時可接近于0。但是，當σ太小時很大，使得u、u的計算結果受u的噪聲影dq響較大，因此σ的取值不宜太小。

2 形態濾波

2.1 形態濾波器的構造

數學形態濾波是建立在數學形態學基礎上，利用結構元素在信號中不斷移動，考察信號各部分之間的相互關系，提取有用特征的方法。形態變換一般分為二值形態變換和灰度(多值)形態變換，其基本運算包括膨脹、腐蝕以及由此引出的開、閉運算等［14-15］。形態運算主要是布爾運算和少量的加減運算，與一般低通濾波器相比，計算簡單且延時短。由于本文的研究對象為電網中的電壓采樣信號，屬于一維多值信號，也可看作是一維灰度圖像，因此下面給出一維灰度形態變換的4種基本運算定義。

設f(x)和b(x)分別為輸入信號和結構元素，長度分別為N和M，且N≥M，則f(x)關于b(x)的腐蝕運算和膨脹運算分別定義為

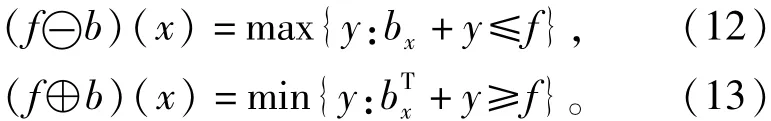
式中，bx表示將沿橫軸平移x的結構元素表示關于原點對稱的結構元素。

從幾何角度講，為求出點x處的腐蝕結果，應將結構元素從原點平移到x點，然后再向上推，始終保持結構元素位于輸入信號的下方，能夠向上推動的最大值即為該點的腐蝕結果。膨脹運算依然與腐蝕運算互為對偶，x處的膨脹結果是通過將b的對稱結構元素bT平移到x處再上推，使得在bTx的定義域內bTx完全位于信號上方(在輸入信號的無定義處，將其值視為負無窮)，此時bTx的上推高度的最小值即為該點的膨脹值。除式(12)和式(13)外，腐蝕和膨脹還有一種在程序上較為容易實現的表達式為

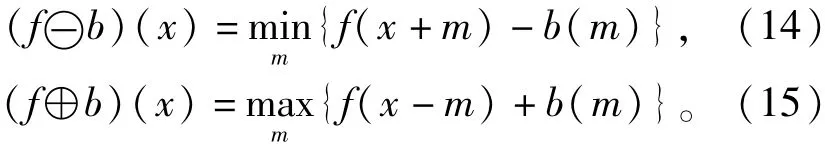
式中結構元素b以m為自變量。

膨脹和腐蝕運算是不可逆運算，先腐蝕后膨脹被定義為開運算;先膨脹后腐蝕被定義為閉運算。利用式(14)和式(15)定義的形態膨脹、腐蝕運算，則一維灰度形態開運算和閉運算可分別定義為

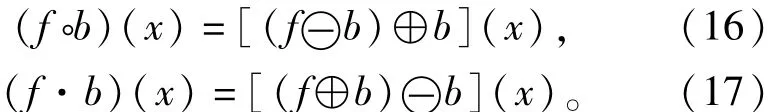
對于含有毛刺噪聲的一維輸入信號，可通過灰度開/閉運算進行濾波。開運算可以從信號波形的下方對波形進行平滑，消除正尖峰噪聲;閉運算則從信號波形的上方對波形進行平滑，消除負尖峰噪聲。而在實際采樣信號中通常同時包含這兩種噪聲。為了能夠同時濾除正、負脈沖噪聲，可對開運算和閉運算進行級聯。由此便形成了開-閉(Oc)和閉-開(co)兩種形態濾波器，其定義分別為

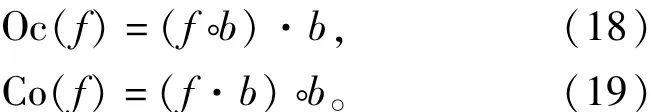
兩種濾波器均有較好的低通濾波效果，但是當噪聲密度較高時，兩種濾波器的輸出均會產生向上或向下的偏移。

根據改進單相dq變換后的電壓信號組成特征，如果選擇合適的結構元素和相應的寬度，則對變換后的信號進行co和Oc運算后，直流分量可以保留，而信號中混雜的寬度小于結構元素寬度的諧波分量將被消除，從而得到暫降深度和相位跳變。同時考慮到co和Oc濾波器均存在統計偏移現象，單獨使用上述兩種濾波器均不能取得理想的濾波效果，因此，為了消除這種偏移，本文采用兩種濾波器平均組合形式，構造混合濾波器為

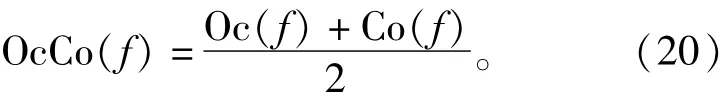
2.2 濾波器結構元素參數選擇

在結構元素的選擇上，要使其盡可能小，同時結構要盡可能接近待分析信號的圖形特點。根據待處理電壓信號的特點，由于要保留的是直流分量，故需采用扁平型結構元素。

實際電網中的電壓信號含有大量的諧波，根據形態濾波器的特點，為僅保留電壓信號中的直流分量，需使結構元素的寬度大于最低次諧波半個周期的寬度。雖然結構元素寬度越長，則濾波器的低通能力越強，濾波效果越好，但是動態響應時間也隨著增大。因此，綜合考慮濾波效果和動態響應時間，結構元素寬度應略大于最低次諧波半個周期的寬度。例如，在采樣頻率為12.8 kHz(每周波采樣256點)的情況下，為了能濾除2次以上的諧波，結構元素的長度取為65較為合適。另外，為減少形態運算的計算量并減少偏移量，結構元素的值選擇為0。

3 方法的實現

綜上所述，采用改進單相dq變換結合數學形態濾波器對電壓暫降進行檢測的算法實現原理如圖1所示。

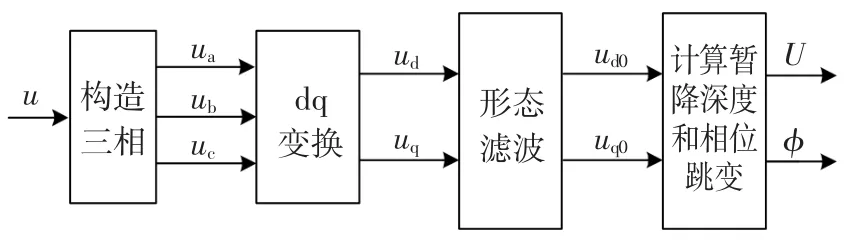
圖1 檢測算法原理Fig.1 Princip le diagram of detection algorithm

用本文提出的新方法對電壓暫降進行檢測的主要步驟如下:

步驟1)將單相系統構造成虛擬的三相系統;

步驟2)根據式(8)將三相電壓變換到d-q旋轉坐標系下，并結合式(9)和(10)得到d軸分量(ud)和q軸分量(uq);

步驟3)利用構造的形態濾波器進行低通濾波得到dq電壓分量中的直流成分ud0和uq0;

步驟4)根據式(11)計算暫降電壓信號的暫降深度和相位跳變。

4 方法性能仿真分析

4.1 理想電壓暫降波形下檢測方法比較

利用Matlab對某一單相電壓暫降采用改進單相d-q變換方法進行檢測，并與目前廣泛應用的有效值法和傳統單相d-q變換方法進行比較。

設定電壓暫降信號表達式為

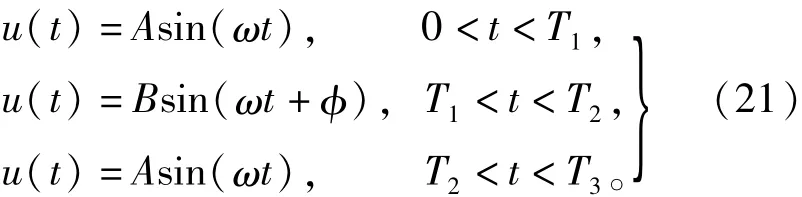
式中，A為暫降發生前和恢復后的電壓瞬時值，B為發生暫降的電壓瞬時值，T1和T2為暫降開始和結束的時間，T3為仿真信號的結束時間，φ為相位跳變。

仿真中設定該相電壓有效值為100 V，頻率為50 Hz，電壓暫降發生在60～160ms之間，暫降深度為50%，暫降起始時刻發生了-60。相位跳變。理想電壓暫降波形如圖2所示，該波形采樣頻率為12.8 kHz(每周波采樣256點)。檢測時改進方法的延時角度取σ=11.25。。

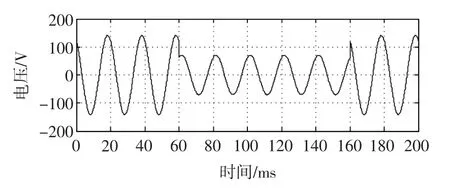
圖2 理想電壓暫降波形Fig.2 Ideal voltage sag waveform

圖3為3種方法電壓暫降深度檢測結果的比較。其中，圖3(a)為有效值法，圖3(b)為傳統單相d-q變換法，圖3(c)為改進單相d-q變換法。

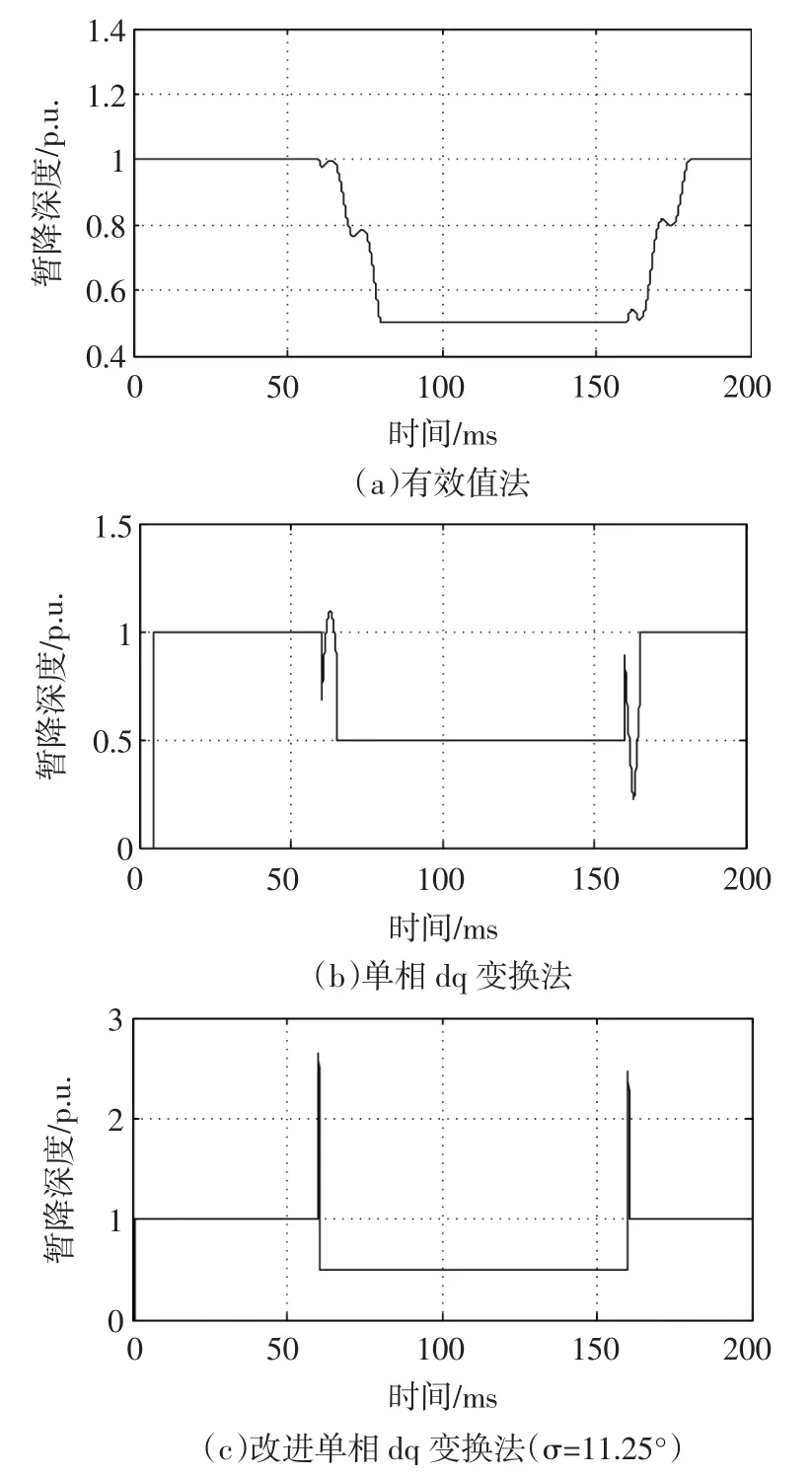
圖3 電壓暫降深度直接檢測結果Fig.3 The direct detection result of sag dep th

由于相位跳變的檢測結果與暫降深度的檢測結果趨勢相同，故文中僅從電壓暫降深度角度對3種方法進行了比較。

由圖3可以看出，有效值法在檢測電壓暫降時，能夠較為準確地檢測出暫降深度值，并且抗噪聲干擾能力較強。但該方法在準確檢測出暫降深度前，會經歷一個周期的過渡期，這是由暫降發生前的“歷史數據”所引起的。過渡期內檢測到的有效值既不是暫降前的正常電壓有效值也不是暫降后的有效值，而是介于二者之間的值。此外過渡期還導致了暫降持續時間的減小，圖中可以明顯看出該方法得到的暫降持續時間比實際少了近一個周期。因此，有效值法雖然在計算暫降深度時較為準確，但不能準確地給出暫降的起止時刻，也無法給出相角跳變。

傳統單相dq變換法可通過兩個間隔90。的采樣點計算得到當前的電壓有效值與相位，對暫降深度及相角跳變的檢測比較精確，計算量很小。但延時大(90。的檢測延時)，實時響應特性不夠好。

改進后的單相dq變換方法，繼承了傳統單相dq變換法的準確度高、計算量小等優點，并在動態響應時間上有了明顯的改善(在本文的算例中檢測延時僅為11.25。)，提高了檢測實時性。但其看抗干擾性能仍較弱，需要后續合理的濾波處理。

3種電壓暫降檢測方法的特點如表1所示。

表1 3種電壓暫降檢測方法特點Table 1 Detection features for three kinds of voltage sags

4.2 含諧波電壓暫降檢測結果濾波效果比較

通常情況下電網中的電壓信號中會有一定的諧波成分，利用改進單相d-q變換進行電壓暫降檢測時，被測電壓u的基波分量表現為ud、uq中的直流量，而u的h次諧波分量表現為ud、uq中的h+1次諧波和h-1次諧波。因此當電壓信號主要含3、5、7次諧波時，經過變換后會變現為2、4、6、8次諧波。這就需要通過低通濾波器濾波以得到ud、uq的直流量ud0和uq0。濾波器會影響到檢測的精度和延時時間。為了驗證本文構造的形態濾波器濾波性能，下面對常用的二階巴特沃斯低通濾波器和本文構造的數學形態濾波器的濾波性能進行比較。

仿真模型中電壓信號的基本參數與無諧波時相同，只是注入諧波成分(5次諧波含量2%，7次諧波含量5%)，含諧波的電壓暫降波形如圖4所示。

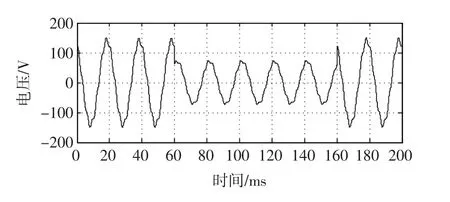
圖4 含諧波的電壓暫降波形Fig.4 Voltage sag waveform w ith harmonic

采用改進單相dq變換結合二階巴特沃斯濾波器與采用改進單相dq變換結合形態濾波器，對電壓暫降檢測結果進行濾波時，檢測到的電壓暫降深度結果如圖5所示，檢測到的電壓暫降相位跳變結果如圖6所示。

通過圖5和圖6中使用巴特沃斯濾波器和使用形態濾波器對電壓暫降結果進行濾波后的結果可以看出:采用傳統巴特沃斯濾波器延時較長，精度也稍差;而形態濾波器延時短，精度也較高，且可以精確確定暫降發生起止時刻，在檢測性能上明顯優于巴特沃斯濾波器。除此以外，形態濾波器的計算量要小于巴特沃斯濾波器。因此在電壓暫降檢測性能上形態濾波器要優于巴特沃斯濾波器。

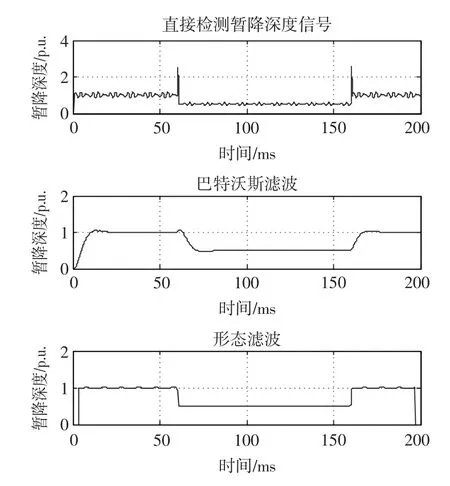
圖5 使用形態濾波器和巴特沃斯濾波器的電壓暫降深度檢測結果濾波效果比較Fig.5 Comparison of filtering effects for detection results of sag depth between m orphological and butterworth filter

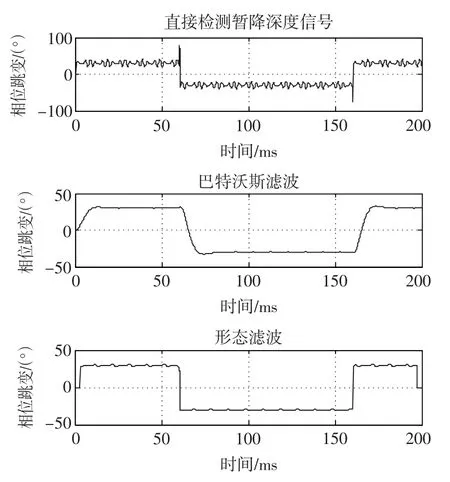
圖6 使用形態濾波器和巴特沃斯濾波器的電壓暫降相位跳變檢測結果濾波效果比較Fig.6 Comparison of filtering effects for detection results of phase angle jum p between morphological and butterworth filter

5 實驗驗證

為驗證方法的有效性，在自行開發的電能質量監測裝置中對所提方法的檢測性能進行了實驗驗證。利用GDS-1102信號發生器的衰減功能產生一個深度為0.1p.u.、相角跳變為0。的電壓暫降信號，在c c S軟件中對裝置的暫降檢測效果進行觀察(采樣率為每周波256點，延時角度為11.25。)。

圖7為裝置通過故障錄波功能記錄的電壓暫降波形，圖8(a)、圖8(b)和圖8(c)分別為與之對應的暫降擾動點、暫降深度、相位跳變檢測結果。

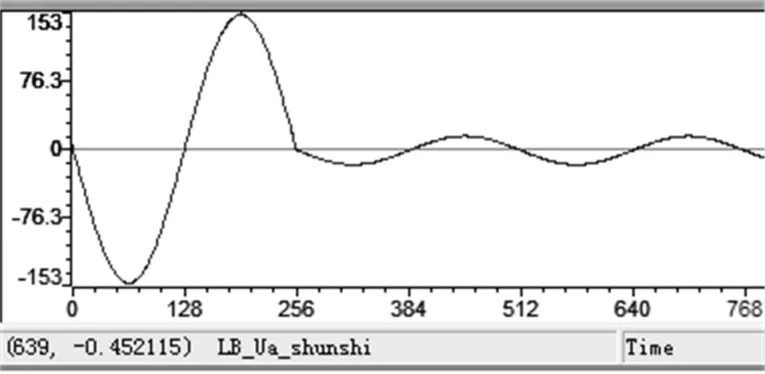
圖7 故障錄波記錄的暫降波形Fig.7 Voltage sag waveform of fault record

從實驗結果可以得出，暫降擾動檢測延時僅為為0.6ms左右，較傳統單相d-q變換法5ms左右的延時有較大提升，暫降深度的檢測誤差小于0.001p.u.，相位跳變的檢測誤差小于0.1。，可見新方法對電壓暫降特征量的檢測具有較高的快速性和準確性。

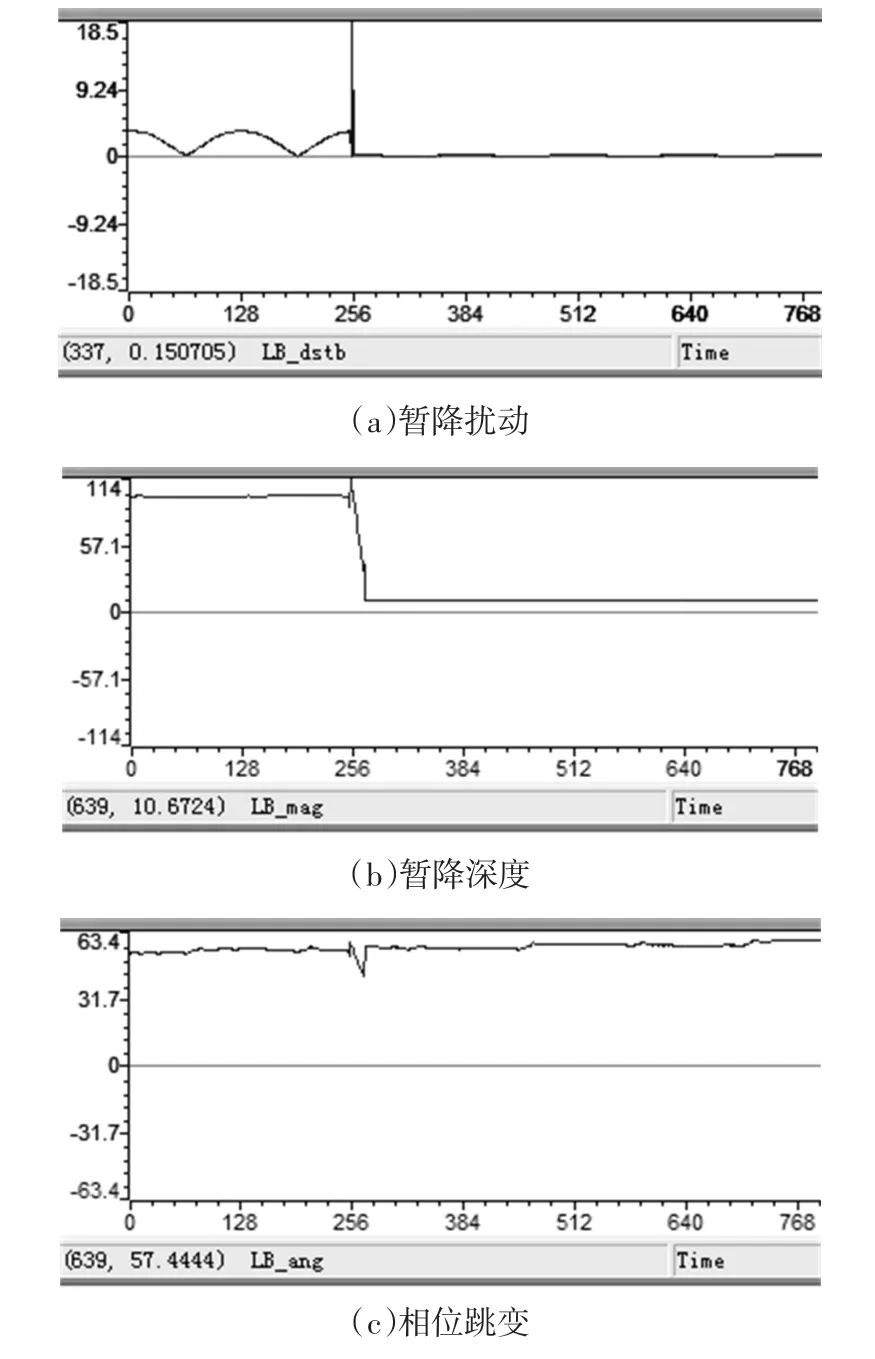
圖8 電壓暫降檢測實驗結果Fig.8 The experimental results of voltage sag detection

6 結 論

本文提出了一種電壓暫降檢測的新方法。改進單相dq變換方法所需的延時角度理論上可以為任意小，較傳統方法能更快速估計電壓暫降發生過程中基波電壓有效值和初相位，檢測精度也較高;形態濾波具有數據處理窗短、運算速度快等優點，所構造的形態濾波器在電壓暫降檢測濾波性能上要優于傳統的低通濾波器。二者的綜合運用，提高了電壓暫降檢測的實時性和準確性，這對動態電壓補償與恢復是有實質意義的。

［1］ 呂干云，孫維蒙，汪曉東，等.利用三點法的電壓暫降源定位方法［J］.中國電機工程學報，2011，31(7):25-26. LüGanyun，SUNWeimeng，WANG Xaiodong，etal.Voltage Sag Source Location Based on Three-point Method［J］.Proceedings of the c SEE，2011，31(7):25-26.

［2］ NIELSEN JG，NEWMAN M.control and testing of a dynamic voltage restorer(DVR)atmedium voltage level［J］.IEEE Trans on Power Electronics，2004，19(3):806-813.

［3］ 曹立志，王小君，和敬涵，等.基于DSP的電壓暫降檢測方法研究［J］.電力系統保護與控制，2012，13:78-83.c AO Li-zhi，WANG Xiaojun，HE Jinghan.Research of voltage sag detection methods based on DSP［J］.Power System Protection and control，2012，13:78-83.

［4］ GOMEZ J c，MORcOSM M.Voltage Sag and Recovery Time in Repetitive Events［J］.IEEE Transactions on Power Delivery，2002，17(4):1037-1043.

［5］ LEE D M，HABETLER TG，HARLEY RG，etal.A voltage sag supporter utilizing a PWM-switched autotransformer［J］.IEEE Trans on Power Electronics，2007，22(2):626-635.

［6］ 劉連光，賈文雙，肖湘寧，等.用小波變換和有效值算法實現電壓凹陷的準確測量［J］.電力系統自動化，2003，27(11):30-33. LIU Lianguang，JIA Wenshuang，XIAO Xiangning，et al.Measurementmethod of voltage sag bywavelet transform and RMSmethod［J］.Automations of Electrical Power Systems，2003，27(11): 30-33.

［7］ 趙鳳展，楊仁剛.基于短時傅里葉變換的電壓暫降擾動檢測［J］.中國電機工程學報，2007，27(10):28-34. ZHAO Fengzhan，YANG Rengang.Voltage sag disturbance detection based on short time Fourier transform［J］.Proceedings of the c SEE，2007，27(10):28-34.

［8］ 李承，楊博，鄒云屏，等.基于反饋神經網絡的電壓暫降特征量實時檢測方法［J］.電機與控制學報，2010，14(9):19-25. LI cheng，YANG Bo，ZOU Yunping，et al.Voltage sag real-time detectionmethod based on feedback neural network［J］.Electric Machines And control，2010，14(9):19-25.

［9］ 劉應梅，白曉民，王文平，等.基于Dyn測度的電壓暫降檢測方法［J］.電力系統自動化，2004，28(2):45-49. LIU Ying-mei，BAIXiao-min，WANGWen-ping，et al.A Dynamics-based method for voltage sags detection［J］.Automations of Electrical Power Systems，2004，28(2):45-49.

［10］ 李智勇，吳為麟.基于分形測度的電壓暫降持續時間檢測［J］.電工技術學報，2007，22(9):148-153. LIZhiyong，WU Weilin.Voltage sag duration detecting method based on fractal numbermeasurement［J］.Transactions of china Electrotechnical Society，2007，22(9):148-153.

［11］ ENRIQUE Perez，JULIO Barros.An extended Kalman filtering approach for detection and analysis of voltage dips in power system［J］.Electric Power Systems Research，2008，78(4):618 -625.

［12］ 常學飛，田立軍，秦英林.一種精確確定電壓暫降凹陷域的算法［J］.電力自動化設備，2011，31(4):64-68. c HANG Xuefei，TIAN Lijun，QIN Yinglin.Method to accurately determine vulnerable areas of voltage sag［J］.Electric Power Automation Equipment，2011，31(4):64-68.

［13］ FITZER c，BARNESM，GREEN P.Voltage sag detection technique for a dynamic voltage restorer［J］.IEEE Trans on Industry Applications，2004，40(1):203-212.

［14］ 陳平，李慶民.基于數學形態學的數字濾波器設計與分析［J］.中國電機工程學報，2005，25(11):60-65. c HEN Ping，LIQingmin.Design and analysis of mathematical morphology-based digital filters［J］.Proceedings of the c SEE，2005，25(11):60-65.

［15］ 歐陽森，王建華，宋政湘，等.基于數學形態學的電力系統采樣數據處理方法［J］.電網技術，2003，27(9):61-65. OUYANG Sen，WANG Jianhua，SONG Zhengxiang，et al.A new power system sampled data processingmethod based onmorphology theory［J］.Power System Technology，2003，27(9):61 -65.

(編輯:于智龍)

A detection algorithm of voltage sag based on improved single-phase dq trans for mation and morphological filtering

JIN Xian-ji， TONGWei-ming， LU Lei， LIFeng-ge
(School of Electrical Engineering and Automation，Harbin Institute of Technology，Harbin 150001，china)

Aiming at the problems of bad real time capability and low accuracy on voltage sag characteristic quantity detecting and combined with mathematicalmorphology and dq transformation，a new algorithm for voltage sag detection was presented，which integrates improved single-phase dq transformation with morphological filtering.The principle of improved single-phase dq transformation algorithm was studied，and amixedmorphological filterwas constructed with structure parameters given.The detection performances of the proposedmethod using in ideal voltage sagwaveform and containing harmonic voltage sag waveform were analyzed by simulating，and the results have been verified through experiments.The results of simulation analysis and experimental verification show that the amplitude and phase angle of voltage sag can be got quickly and accurately by using improved single-phase dq transformation and morphological filtering is used to remove Ac componentswhich is low computational complexity and high precision.

smart grid;voltage sag;morphological filtering;dq transformation;phase angle jump

10.15938/j.emc.2015.04.008

TM 761

A

1007-449X(2015)04-0046-07

2014-01-16

國家自然科學基金(51077015，50907014);中央高校基本科研業務費專項資助(HIT.NSRIF.2015017)

金顯吉(1982—)，男，博士，助理研究員，研究方向為電能質量監測，電力系統信息及通信技術;俘為明(1964—)，男，博士，教授，博士生導師，研究方向為電氣智能化技術，變電站自動化等;盧 雷(1987—)，男，博士研究生，研究方向為電力系統信息安全;李鳳閣(1967—)，女，碩士，高級工程師，研究方向為電力系統自動控制。

俘為明