基于補償分量的MMC最大調制系數的分析

劉一琦， 李寧寧， 傅裕， 王建嘖， 紀延超

(哈爾濱工業大學電氣工程及自動化學院，黑龍江哈爾濱150001)

基于補償分量的MMC最大調制系數的分析

劉一琦， 李寧寧， 傅裕， 王建嘖， 紀延超

(哈爾濱工業大學電氣工程及自動化學院，黑龍江哈爾濱150001)

針對模塊化多電平換流器(MMc)的相間環流問題，提出基于補償分量的調制方法以便于降低MMc調制系數中的基頻分量。首先通過結合實際系統中電容參數設計和換流器的正常運行范圍，對MMc子模塊電容電壓紋波進行取值并求解其最大值，然后分析調制系數中抑制環流的補償分量與電容電壓紋波之間的數量關系，最終得到MMc最大調制系數的取值范圍。仿真和實驗驗證的結果表明，通過對含有補償分量的最大調制系數范圍的確定，系統環流得到了有效抑制，避免了過調制現象的發生，有利于MMc系統的穩定運行。

補償分量;環流抑制;模塊化多電平換流器;調制系數;電容電壓紋波

0 引 言

近年來隨著風能和太陽能等可再生能源在分布式發電和大規模電站中的廣泛應用［1］，電力電子變換器技術得到了快速發展，高壓大功率能量轉換系統的需求也日益增長［2-4］。模塊化多電平變換器(modular multilevel converter，MMc)是一種新穎的多電平變換器拓撲結構，通過將多個相同子模塊串聯在一起，具有控制簡單、存在公共的直流側、突破了功率半導體器件容量的限制等優點，已成為高壓大功率電能變換應用領域中的一種理想的解決方案［5-7］。但由于MMc在工作過程中，子模塊電容的充放電導致了MMc的每相橋臂輸出電壓不同。因此，MMc存在子模塊電容電壓的均壓、環流等明顯的問題。其中，環流主要是由二倍頻諧波分量構成［8-10］，采用開環的調制方法，從理論上消除了環流，但難點在于需要得到各電容電壓的精確估計值［11］。閉環的調制方法［12］與開環的調制方法類似，都是引入一個附加分量到橋臂電壓參考值中，補償子模塊電容電壓的變化［13-14］。為了避免對MMc交流側的影響，這個補償分量被等量地加到上(下)橋臂中。

MMc的橋臂電壓參考值由一個恒定的直流電壓和一個基頻分量組成。基頻分量的幅值反映了換流器的調制系數，因此對橋臂電壓參考值的限制決定了調制系數的大小。由于環流控制引入了補償分量到橋臂電壓參考值中，因此需要減小MMc調制系數的最大值從而避免過調制，但同時也降低了直流電壓利用率，這在高壓直流輸電應用中是一個嚴重的問題。本文在考慮了環流抑制的前提下，詳細地分析了MMc的數學模型，然后通過理論推導得到了含有補償分量的子模塊投入系數，基于上面的分析和投入系數的求解，得到了基于補償分量法的最大調制系數的取值范圍。最后通過比較仿真和實驗結果驗證了其正確性和合理性。

1 MMC的廣義動態建模

三相MMc系統結構如圖1所示。

MMc的子模塊由2個帶有反向續流二極管的全控型開關器件和1個直流儲能電容構成［12］。通過采用平衡控制方法，假設每相橋臂上的不同子模塊的電容電壓相同。因此，MMc的每相橋臂電壓可以表示為

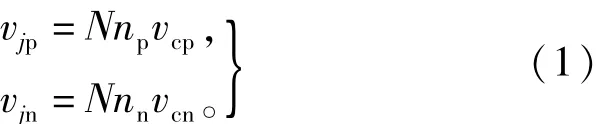
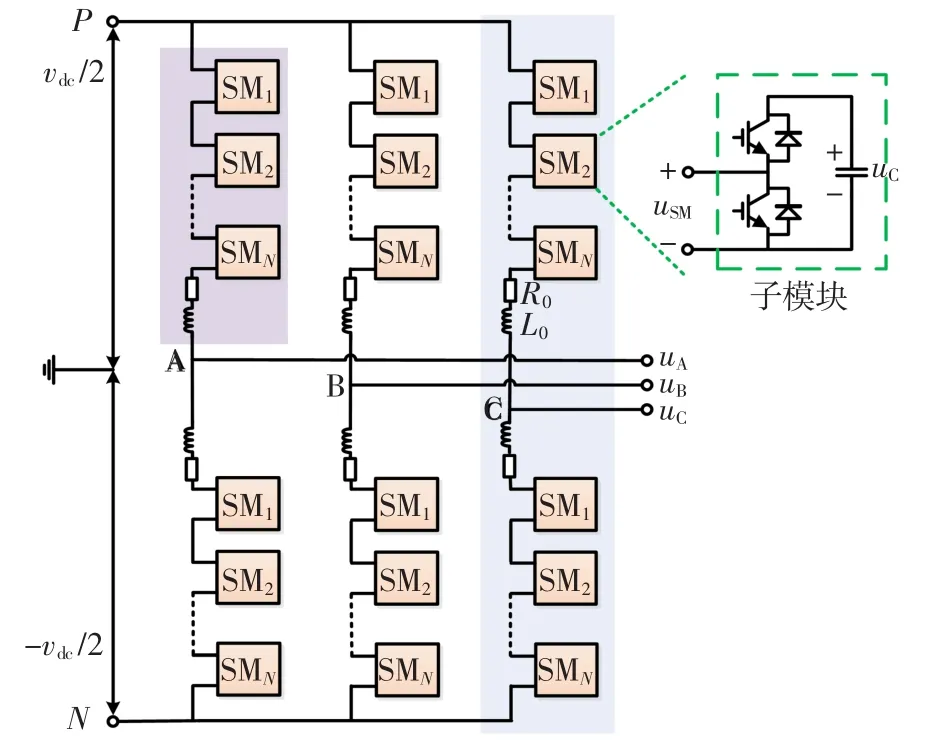
圖1 三相MMC系統結構示意Fig.1 Three phase MMC main circuit structure

其中np和nn是投入系數。N是上(下)橋臂子模塊的總數，vcp和vcn是上(下)橋臂子模塊電容電壓值，流過上(下)橋臂子模塊的電流［15］可表示為

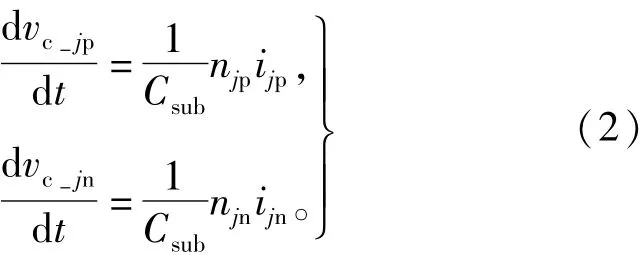
分別對第j相上(下)橋臂應用基爾霍夫電壓定律可得

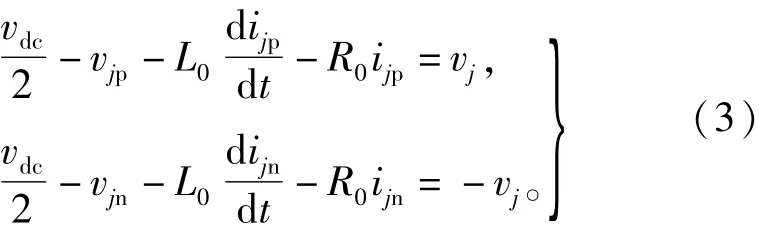
其中:L0和R0是橋臂電感與橋臂電阻，vdc是MMc的直流側電壓。由式(3)可知MMc交流側和直流側的電壓模型為

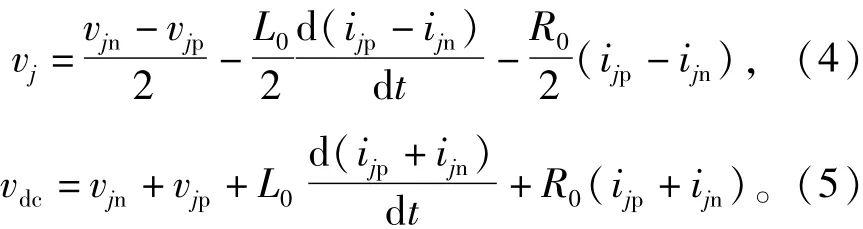
文獻［16］中提出，由于環流控制會導致系統損耗增加，所以在投入系數中引入一個補償分量，可以實現降低系統損耗。因此，含環流抑制的投入系數可定義為

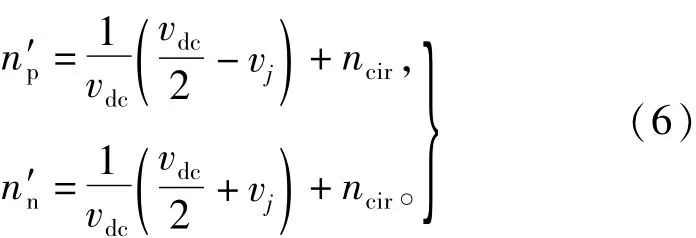
由式(6)可知，式(3)可以簡化為

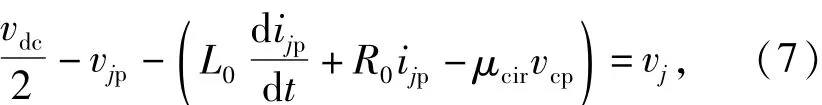
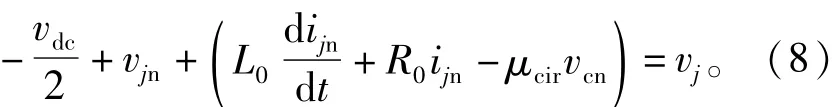
結合式(7)和式(8)，直流側和交流側等效模型如下:

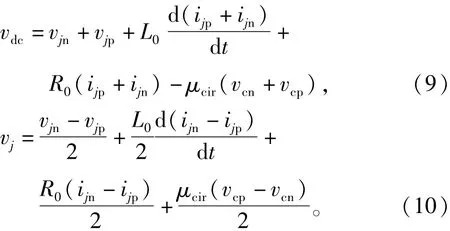
2 穩態值計算

在MMc中，通常將交流側電流、直流側電壓和環流作為控制目標，結合上文中得到的數學模型，vcp+ccn，vcp-vcn的穩態值可以進行理論計算。然而，由于系統中同時存在基頻分量和二次諧波分量使穩態值不能做到十分精確。首先可以忽略子模塊電容電壓紋波:

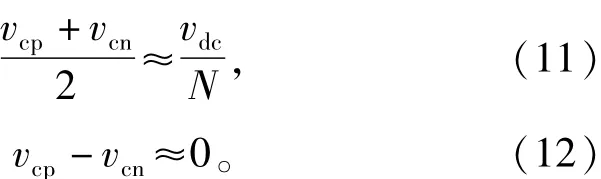
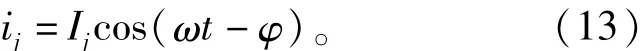
其中φ代表交流相電壓和相電流的功角。

假設換流器無損耗，通過直流側和交流側的功率平衡:

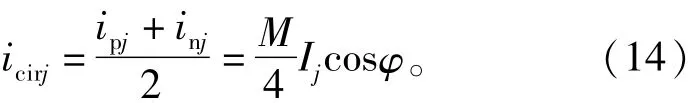
如果比較式(11)，式(12)中的近似值，可以發現最初的假設只有當Csub足夠大時才能成立。從實際應用設計的角度考慮，Csub不可以太大否則換流器的成本會大大地增加。實際設計中將限制最大電容電壓紋波在10%左右。電容電壓紋波為［17］

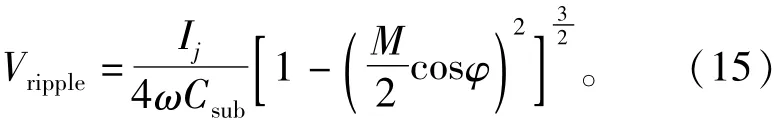
式(5)表明最大電容電壓紋波取決于換流器運行范圍，最大無功功率一般被定義為最大視在功率的一半，所以MMc運行在滿載視在功率時最小功率因數為因此可以得到最大電容電壓紋波

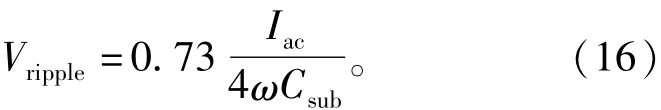
其中M的最大值為1，系數0.73與最大無功功率的約束相關。

如上述可知，環流控制將會加入一個補償分量ncir到np和nn中。這個附加分量將會對上、下橋臂的投入系數產生影響，以至于影響MMc的調制系數的最大值。

3 補償分量下調制系數最大值的計算

3.1 補償分量的計算

被控的ijp+ijn只含有直流分量，考慮到R0相對很小，式(9)可簡化為

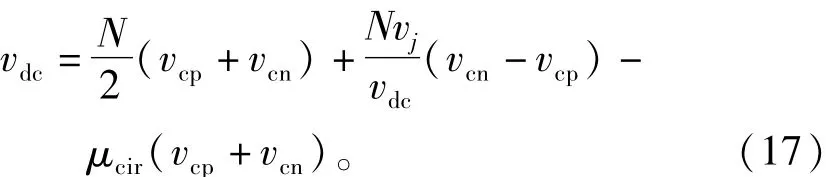
因此將式(11)帶入上式得

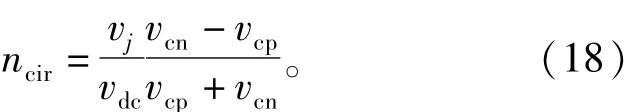
結合式(2)，式(6)，式(11)、式(12)和式(14)可得

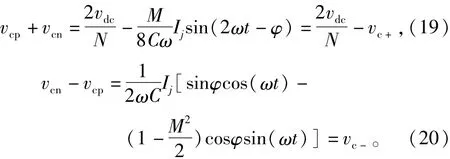
將式(19)和式(20)代入式(18)可以求得補償分量的表達式為

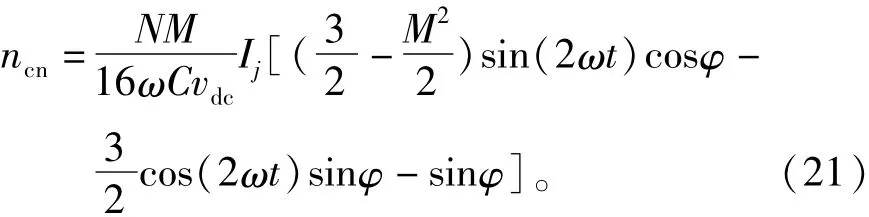
式(21)表明補償分量是一個二倍頻諧波，與系統參數(Csub、N)和運行條件(M、Iac和φ)有關。所以評估其對調制信號的影響并不方便。下面的數學運算可以用來簡化ncir的表達。基于式(16)，子模塊電容電壓紋波的相對最大值可以被定義為

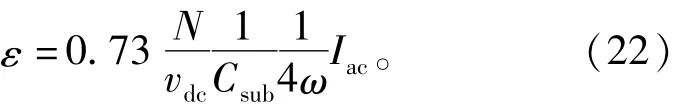
由于ε可以被看成一個固定值，則式(21)可以被簡化為

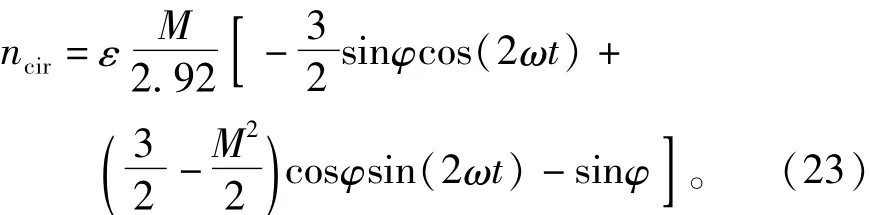
3.2 調制系數最大值的計算

上(下)橋臂的投入系數可以通過式(6)可得

投入系數應該滿足:

根據式(26)，上、下橋臂投入系數的最大和最小值可以在cosφ等于最小值的時候得到

所以可以得到調制系數的約束方程為

式(29)表明，調制系數最大值小于1，并且電容電壓紋波越大會導致損耗越大。可以得出結論，如果假設子模塊電容電壓紋波為10%，則使用環流控制后調制系數的最大值將減少8%(從1到0.92);這些削減是不可以忽視的，而應該在MMc設計階段就被考慮于額定調制系數的選取中。

4 仿真驗證

為了驗證上述理論計算和分析的正確性和可行性，在Matlab/SIMULINK仿真軟件中搭建了MMc并網逆變器的模型。采用NLM調制策略，上(下)橋臂取反向的三角波與調制波進行比較，避免同向三角波與調制波進行比較過程中出現調制間隙導致開關器件頻繁切換，減少切換損耗。系統參數見表1。

表1 MMC-HVDC系統參數Table 1 The parameters of MMC-HVDC system.

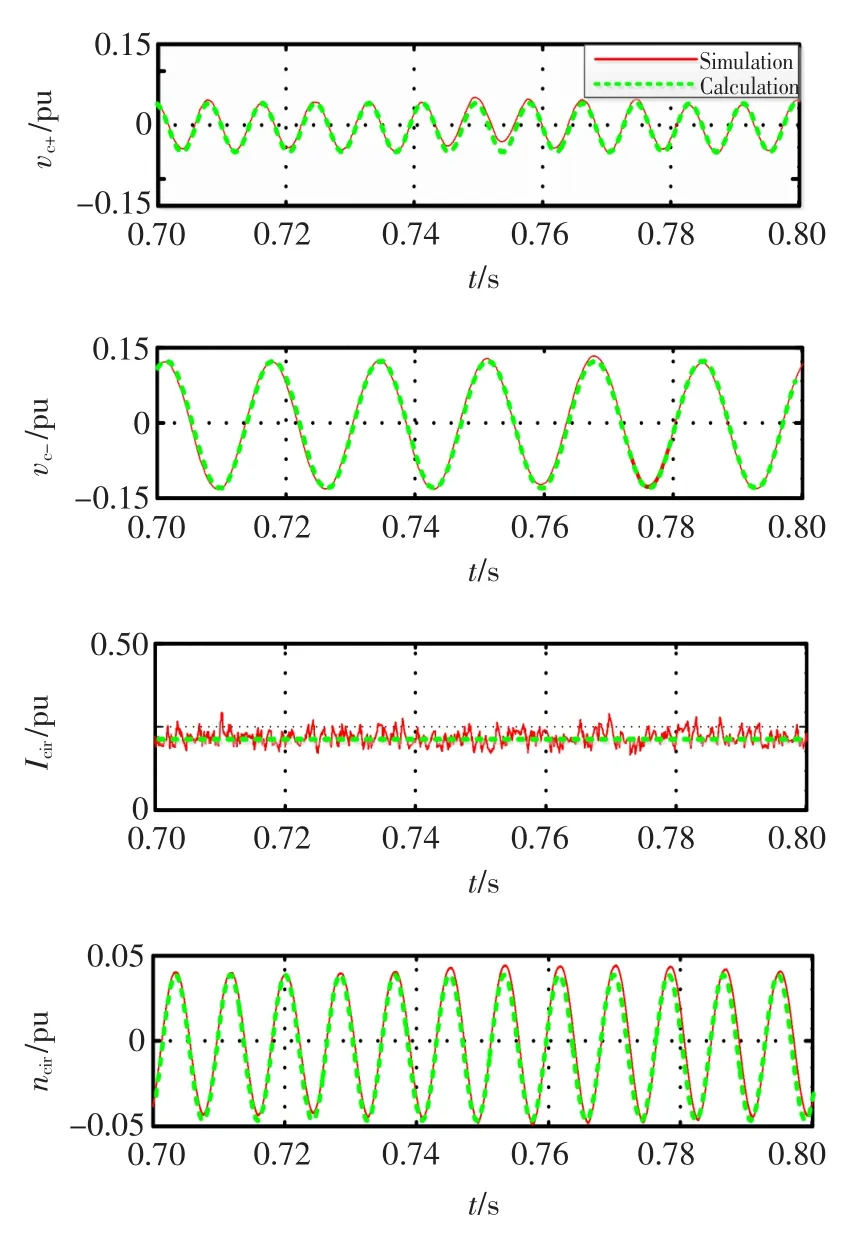
圖2 穩態仿真結果Fig.2 Simulation results of steady state

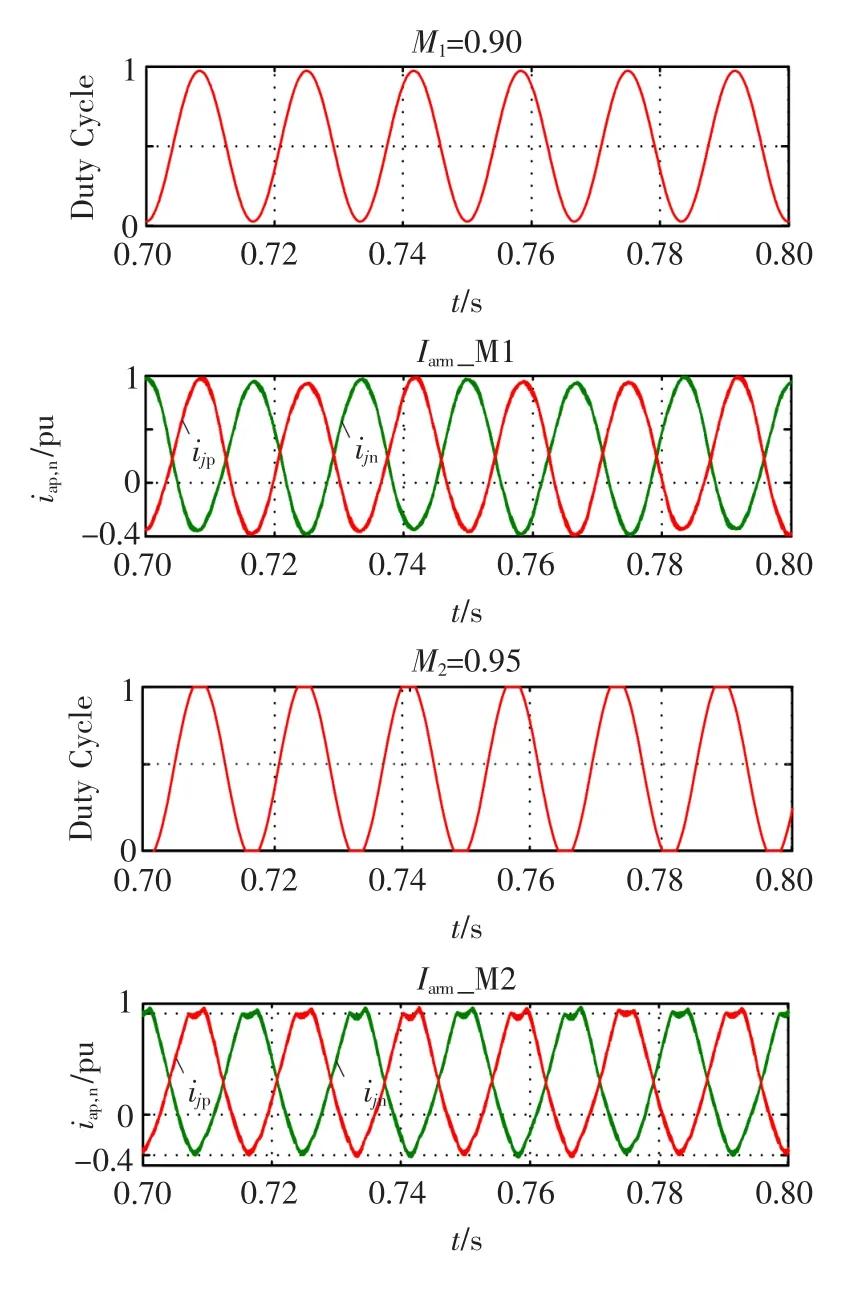
圖3 在不同調制比條件下的電流信號Fig.3 The current signalwith differentmodulation indices

5 實驗驗證

為了驗證MMc模型和調制系數最大值的正確性，研制了1 kW三相五電平的MMc實驗樣機，上(下)橋臂各有2個子模塊，額定直流電壓為100 V，子模塊電容值為2 700μF，橋臂電感值為0.26mH。MMc直流側連接一個恒定的直流電壓源，運行在逆變狀態，交流側連接三相平衡的無源阻感負載。每相的電阻值為3.3Ω，電感值為5.5mH，為了模擬下限的運行情況，功角設定為30。。

在該樣機中，由于死區的要求，每橋臂的調制指數最大值被限制到了0.98。在上述的系統參數下，相對電容電壓波動設計越大，調制系數將越小。圖4(a)說明了MMc達到穩態運行時，當調制系數按上述推導設定到約束條件的最大值0.92時，交流側輸出電壓、電流和上(下)橋臂電流波形處于穩定運行狀態，而MMc系統的相間的環流出現少數鋸齒狀波形，說明調制系數已經達到最大，如果超過0.92將會出現過調制現象。圖4(b)是對投入系數中加入補償分量后MMc子模塊電容電壓達到均衡運行的實驗結果。因此可以證明，實驗和仿真結果與理論分析基本一致，驗證了理論分析的正確性和合理性。

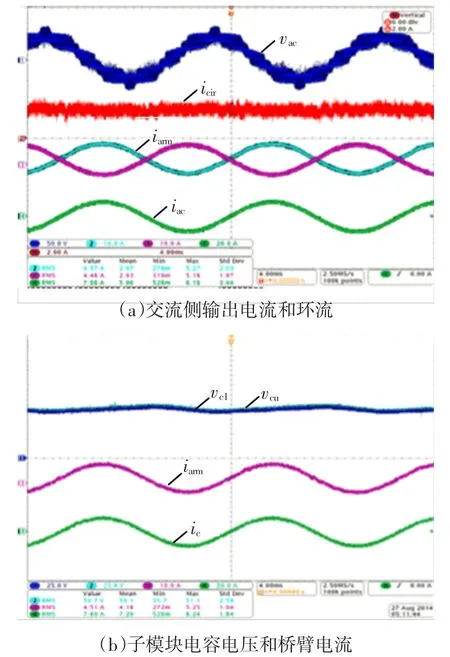
圖4 穩態實驗結果Fig.4 Experimental results of steady state

6 結 論

通過添加一個補償分量為二倍頻的補償系數到含有環流控制的調制信號中，這個補償分量會調節換流器最終的調制系數的大小，這將影響直流電壓的利用率。因此得到調制系數最大值的削減量與子模塊電容值有關，越小的電容值會導致越大的削減。如果電容被設計成滿足10%的電壓紋波要求，那么調制指數的最大值將減少8%。這個削減量不能被忽視，而應該在換流器設計時就考慮到額定調制系數的選取中。對于調制系數的合理考慮設計，會對系統的穩定運行和電容電壓的均衡控制均會起到更佳的效果，保證了系統穩定運行的安全性和提高了系統功率傳輸的可靠性。

［1］ XIAONAN L，GUERRERO JM，KAIS，et al.Hierarchical control of parallel Ac-Dc converter interfaces for hybrid microgrids［J］.IEEE Transactions on SmartGrid，2014，5(2):683-692.

［2］ JM cARRAScO，L G FRANQUELO JT.BIALASIEWIcZ，et al. Power-electronic systems for the grid integration of renewable energy sources:A survey［J］.IEEE Transactions on Industrial Electronics，2006，53(4):1002-1016.

［3］ X LU，K SUN，JM.GUERRERO，et al.State-of-charge balance using adaptive droop control for distributed energy storage systems in Dc micro-grid applications［J］.IEEE Transactions on Industrial Electronics，2014，6(61)，2804-2815.

［4］ M GLINKA，RMARQUARDT.A new Ac/Dc multilevel converter family［J］.IEEE Transactions on Industrial Electronics，2005，52(3):662-669.

［5］ 劉鐘淇，宋強，劉文華.基于模塊化多電平變流器的輕型直流輸電系統［J］.電力系統自動化，2010，34(2):53-58. LIU Zhongqi，SONG Qiang，LIU Wenhua.VSc-HVDc system based onmodularmultilevel converters［J］.Automation of Electric Power Systems，2010，34(2):53-58.

［6］ 管敏淵，徐政.模塊化多電平換流器型直流輸電的建模與控制［J］.電力系統自動化，2010，34(19):64-68. GUAN Minyuan，XU Zheng.Modeling and control ofmodularmultilevel converter in HVDc transmission［J］.Automation Power Systems，2010，34(19):64-68.

［7］ 管敏淵，徐政，屠卿瑞，等.模塊化多電平換流器型直流輸電的調制策略［J］.電力系統自動化，2010，34(2):48-52. GUAN Minyuan，XU Zheng，TU Qingrui，et al.Nearest levelmodulation for modular multilevel converters in HVDc transmission［J］.Automation of Electric Power Systems，2010，34(2):48 -52.

［8］ QINGRUI TU，ZHENG XU，LIE XU.Reduced switching-frequencymodulation and circulating current suppression formodular multilevel converters［J］.IEEE Transactions on Power Delivery，2013，26(3):2009-2017.

［9］ 屠卿瑞，徐政，鄭翔，等.模塊化多電平換流器型直流輸電內部環流機理分析［J］.高電壓技術，2010，36(2):547-552.

TU Qingrui，XU Zheng，ZHEN Xiang.et al.Mechanism analysis on the circulating current in modular multilevel converter based HVDc［J］.High Voltage Engineering，2010，36(2):547-552.

［10］ DORN J，HUANG H，RETZMANN D.A new multilevel voltage sourced converter topology for HVDc applications［c］//c I2 GRE Session.Paris，France:c IGRE，2008.

［11］ L ANGQUIST，A ANTONOPOULOS，D EMASZKO，et al. Open-loop control ofmodularmultilevel converters using estimation of stored energy［J］.IEEE Transactions on Industry Application.，2011，47(6):2516-2524.

［12］ A ANTONOPOULOS，L ANGQUIST，H P NEE.On dynamics and voltage control of the modular multilevel converter［c］//in Proc.European conf.Power Electronics and Applications (EPE)，Sept.2009:1-10.

［13］ YALONG L，EDWARD A JONES，FRED WANG.Switchingfrequency ripple in dc link voltage in a modular multilevel converter with circulating current suppressing control［c］//Proc. Applied Power Electronics conference and Exposition (APEc)，2014.

［14］ YALONG L，FREDWANG.Arm inductance selection principle for modular multilevel converters with circulating current suppressing control［c］//Proc.Applied Power Electronics conference and Exposition(APEc)，2013.

［15］ K.ILVES，A ANTONOPOULOS，S NORRGA，et al.Steadystate analysis of interaction between harmonic components of arm and line quantities ofmodular multilevel converters［c］//IEEE Transactions on Power Electronics，2012，27(1):57-68.

［16］ YALONG L，EDWARD A.JONES，FRED WANG.Analysis of the relationship between switching frequency and sub-Module capacitor unbalanced voltage for a modular multilevel converter［c］//Proc.Applied Power Electronics conference and Exposition(APEc)，2014.

［17］ S.ENGEL，RW DE DONc KER.control of themodularmultilevel converter forminimized cell capacitance［c］//in Proc.European Power Electronics and Application conference，2011.

(編輯:劉素菊)

Maximum modulation index analysis of MMC based on compensating component

LIU Yi-qi， LINing-ning， FU Yu， WANG Jian-ze， JIYan-chao
(School of Electrical Engineering and Automation，Harbin Institute of Technology，Harbin 150001，china)

Aiming at the circulating current in modular multilevel converter(MMc)，the modulation method was proposed based on compensating components to reduce the fundamental component in the modulation index.First，considering the parameter of capacitor design and the range of converter operation in practical system，capacitor voltage ripple in MMc was calculated，its maximum value was derived，and then the relationship between compensating component for eliminating circulating current in modulation index and capacitor voltage ripple was analyzed.Finally，the range of themaximum modulation index for MMc was obtained，and the simulation and experimentwere performed to verify the theoretical results.It is shown that by confirming the maximum modulation index with the compensated term，the circulating current can be effectively eliminated.At the same time，over-modulation is avoided，which ensures the stable operation of MMc.

compensating component;circulating current control;modularmultilevel converter(MMc); modulation index;capacitor voltage ripple

10.15938/j.emc.2015.04.009

TM 46

A

1007-449X(2015)04-0053-05

2014-09-06

科技部國際科技合作計劃資助項目(2010DFR70600)

劉一琦(1984—)，男，博士研究生，研究方向為可再生能源功率變換和高壓直流輸電技術等;李寧寧(1982—)，男，博士研究生，研究方向為無功功率補償，蓄電池儲能等;傅 裕(1990—)，男，碩士研究生，研究方向為可再生能源功率變換和無功功率補償技術等;王建賾(1972—)，男，研究員，研究方向為無功功率補償、清潔能源并網控制等;紀延超(1962—)，男，教授，博士生導師，研究方向為無功功率補償、有源濾波技術等。

劉一琦