風力機非定常氣動力降階模型

郭 強，劉鵬寅，竺曉程

（1.上海汽車集團股份有限公司乘用車公司，上海201804；2.上海交通大學機械與動力工程學院，上海200240）

眾所周知，準確的非定常氣動力模型是風力機氣彈設計的重要組成部分.而氣彈的不穩定和顫振是風力機設計必須考慮的問題，因此準確預測風力機葉片所受動態氣動載荷在風力機設計中尤為重要.由于整個設計流程是一個不斷迭代的過程，因此所需的氣彈計算模型不僅要準確而且要快速，尤其是對于氣彈現象復雜的風力機葉片［1］.風力機葉片的非定常氣動載荷主要是由于在自然環境中，大氣紊流、塔架影響、地面邊界層效應以及偏航工況等因素影響，使得風力機葉片處于非定常流動區域.在此情況下，葉素的有效攻角在不斷變化，并會導致動態氣動載荷的出現.

這一動態氣動載荷的特征取決于邊界層是附著還是分離.如果葉片表面流動是附著的，翼型所受的動態氣動載荷與靜態氣動載荷差別不大，主要表現為一種延時現象.如果葉片表面流動出現分離，葉片振動將使得有效攻角呈非定常變化，同時導致動態失速的發生.在流動分離工況下，翼型的動態氣動載荷和靜態氣動載荷會有相當大的區別，動態失速使葉片所受的最大氣動載荷大大增加.而隨著風力機直徑的增大，過大的氣動載荷增加了風力機穩定控制的難度.從穩定方面考慮，至少在升力預測時需要加入動態失速模型以減小預測誤差［2］.

從非定常氣動力預測精度來看，隨著計算機技術的顯著進步以及數值計算和湍流模型方面所取得的進展，通過CFD 方法來研究非定常氣動力的動態響應變得越來越切實可行.大量這方面的工作［3-5］不僅對了解非定常氣動力的變化發展有積極作用，同時也證明了CFD 方法在常規風力機和直升機槳葉設計中必會起到越來越重要的作用.但是較高精度的CFD 方法需要較高的計算成本.

因此，依靠少量數值計算算例結果建立預測模型，并對其他工況進行預測模擬的方法逐漸引起研究人員的興趣.降階模型方法是這類非定常氣動力預測模擬方法中較常用的一種，常用的2種降階模型有：ARMA 模型［6］和Volterra級數模型［7］.這類方法的主要優點是其精度可隨著CFD 方法的改進而提升.當流動復雜程度增加時，基于高適用性的CFD 方法的降階模型將比半經驗模型更為可靠.

由于三維問題的復雜程度較高，筆者將風力機葉片的動態氣動載荷問題簡化為二維翼型進行振蕩運動時的氣動力變化.在附著流動和分離流動情況下，分別對翼型的升力系數采用2種不同降階模型進行預測，并將預測結果與CFD 計算結果進行對比，以驗證降階模型的有效性.

1 CFD計算

采用帶轉捩修正的k-ωSST 湍流模型.圖1為計算所用的網格和翼型表面附近的網格.采用三角形和四邊形混合的網格，整個計算區域分為外部靜止區域（簡稱外部區域）和內部圍繞翼型振蕩的運動區域（簡稱內部區域）.外部區域全部采用四邊形網格，內部區域采用三角形和四邊形混合網格.為了減小界面通量傳遞的插值誤差，內、外區域交界面具有相同大小和數量的一致網格.翼型周圍采用C 型四邊形邊界層網格，翼型表面網格節點總數為400.第一層網格的布置確保y＋在1.0量級處，且保證網格的法向膨脹率不大于1.1.外部進、出口邊界位于距翼型約20倍弦長處.入口邊界設置速度分量及合適的入流湍流度，出口邊界為靜壓力邊界，翼型表面的邊界條件為振蕩運動的無滑移壁面.經過時間步長無關性檢查，采用的時間步長為0.001s，每個工況都至少經過5個連續周期的計算以得到周期性穩定的流場［4］.需要指出的是這樣一個非定常工況的CFD 計算需要十幾個小時，對于需要大量工況數據的設計和優化工作而言計算成本較高.

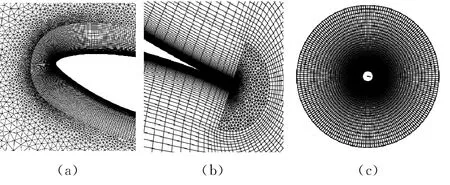
圖1 計算網格Fig.1 Computational mesh

2 降階模型

2.1 ARMA 模型

ARMA 模型將某時刻動態氣動載荷的響應認為是當前時刻的動態輸入和前幾個時刻的動態輸入與響應的線性組合.因此當前時刻的動態響應可以表示為：

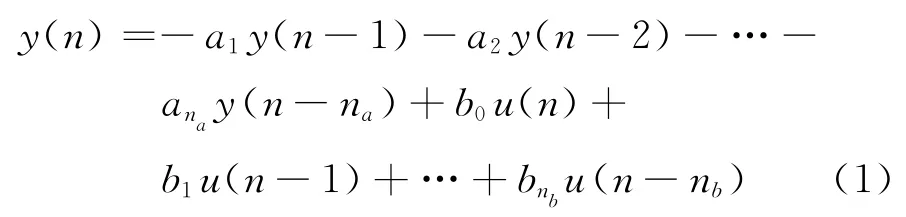
式中：u（n）為動態輸入，此處認為是n時刻的攻角；y（n）為非定常狀態的動態氣動載荷響應，在本文中響應y為升力系數；na和nb分別為可自定義的模型的階數；ani和bni為待辨識的模型參數.

將式（1）以矩陣形式給出，可得到ARMA 模型的另一表達式：

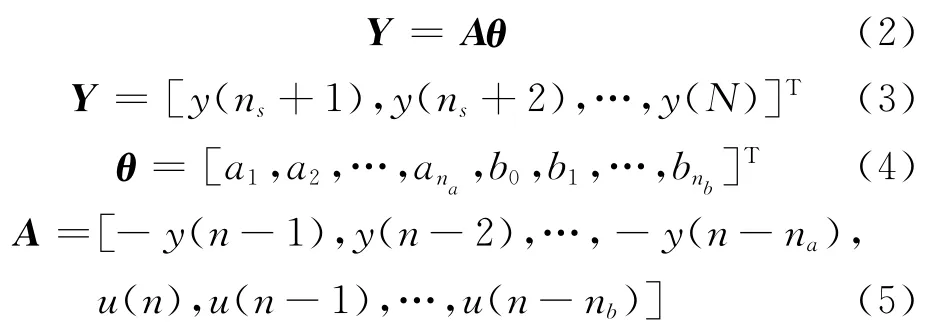
式中：n＝ns＋1，ns＋2，…，N；ns＝max［na，nb］；N為離散時間步的總數.

采用最小二乘法進行辨識，可以得到模型的未定參數：

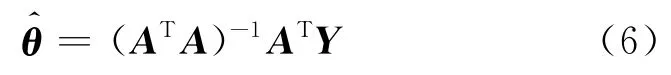
通過以上方法提取一個工況算例的數據作為樣本，通過辨識得到ARMA 模型的待定參數，從而建立ARMA 模型，并依靠建立的ARMA 模型對其他工況的動態響應進行預測.

2.2 Volterra級數模型

Volterra級數模型是較常用的非線性響應模型.對一個離散系統來說，輸入響應可由式（7）表示：

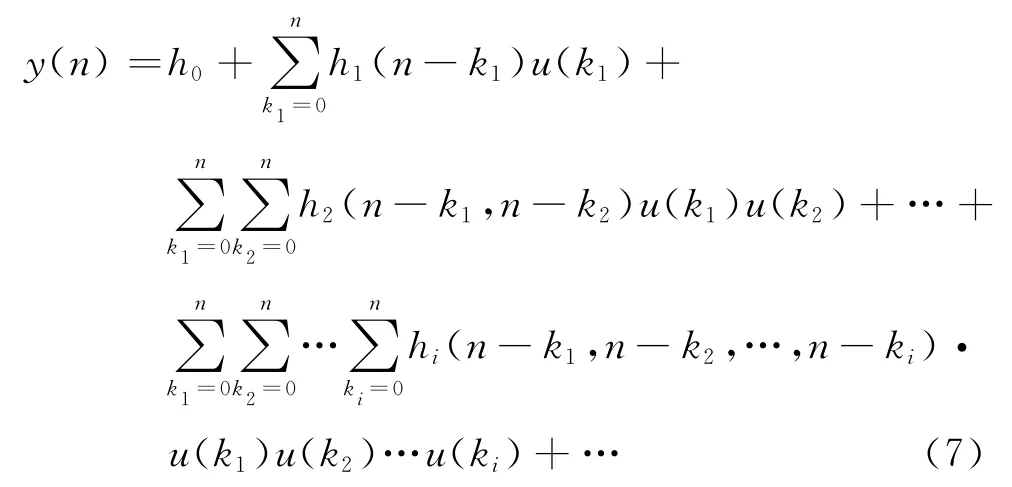
式中：h0為穩態響應值；hi（n-k1，n-k2，…，n-ki）為第i階Volterra核.

由于Volterra核隨階數的變化呈指數增長，求解高階的Volterra核需要較高的計算資源確定，所以對于一個非線性系統，二階或三階Volterra級數是最常用的模型.筆者選用二階Volterra級數模型.

設定一個記憶長度M，二階的Volterra級數可以變化為

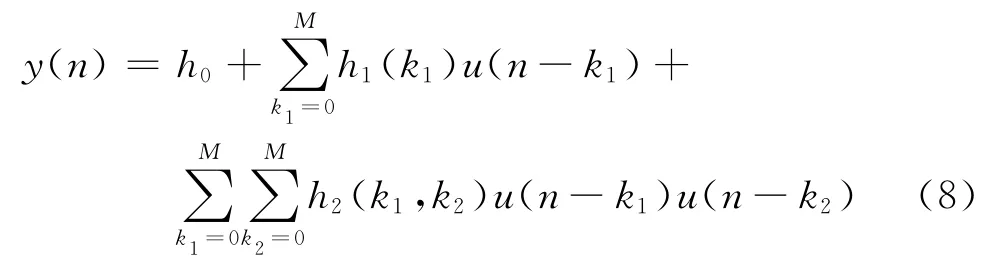
若將輸入以矩陣形式表示：

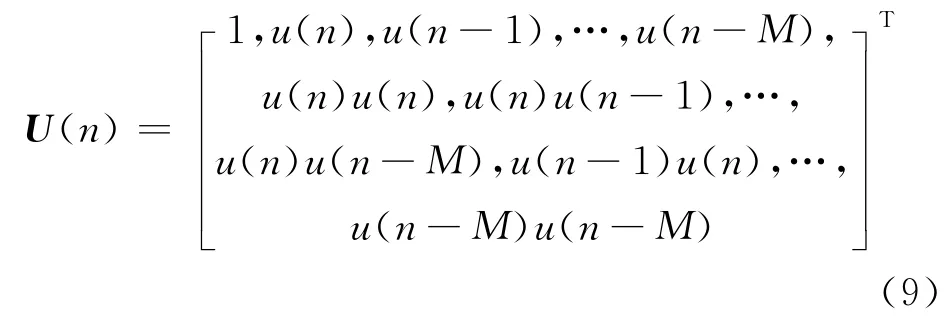
由此可以將二階的Volterra級數模型改寫為矩陣形式：

其中

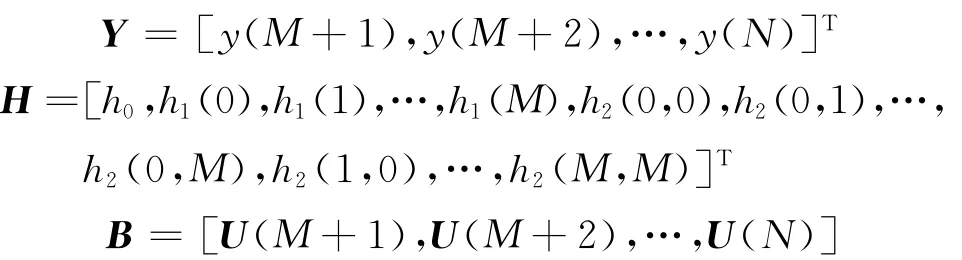
這樣待辨識的模型參數就可由最小二乘法得到：

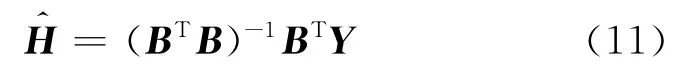
一旦辨識得到各階Volterra核，就可以建立Volterra級數模型并預測非定常氣動載荷.需要特別指出的是，以上2個模型的辨識所需時間在1～2 min內，而模型建立后預測某一工況結果所需的時間在幾秒鐘左右.

3 不同工況的降階模型預測

采用S809翼型進行計算，其靜態失速攻角在10°左右.該翼型的升力系數在失速攻角（最高值）附近保持一段較高的數值，而阻力系數在很大的攻角變化范圍內較小.這些特性使得翼型在變工況下保持較好的氣動特性.為了得到動態失速下的翼型非定常氣動載荷，定義風力機翼型繞轉軸（x／c＝0.25）周期振蕩的變化形式為：

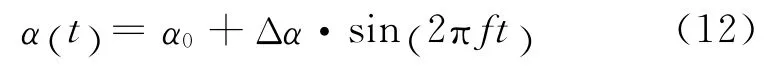
式中：α0為振蕩的平均攻角；Δα為振蕩的振幅；f為振蕩頻率.

同時定義衰減頻率為

式中：c為弦長；U為來流速度.

衰減頻率反映了沿翼型弦向的主流運動和繞轉軸的振蕩運動之間的相互作用，其值表征振蕩運動對主流運動影響的大小，所以當給出振蕩的平均攻角、振幅和衰減頻率后，某一特定翼型的振蕩變化就可以確定.

所有模型的辨識數據都是由CFD 數值計算得到的.對每個非定常氣動計算結果，定義時間t0和tf為觀測的初始和終止時刻.對一個周期內的數據進行處理后得到：

3.1 流動附著工況

將α0＝4°、k＝0.050和Δα＝2°工況下的CFD計算作為樣本，根據式（6）建立ARMA 模型.由于更高的階數已不能提高模型的精度，通過對比選取na＝2，nb＝1.當翼型在這一小攻角（遠小于靜態失速攻角）處振蕩時，流動未發生分離，因此升力系數的變化十分平緩，非線性現象很輕微.這種情況下采用模擬弱非線性系統的ARMA 模型進行動態氣動載荷的預測較有效.

圖2給出了樣本工況的升力系數隨攻角變化的氣動力遲滯回線.由圖2可知，與靜態不同，在附著流動時，同一攻角下升力系數在上仰和下俯過程中是不相同的.升力系數在整個翼型振蕩周期內形成一個橢圓形的氣動力遲滯閉環.由于流動處于附著狀態，所以動態升力系數與靜態升力系數在數值上差別不大.在非定常和定常升力之間存在一個時間延遲，這一時間延遲可以由Theodorsen理論計算得到.比較ARMA 模型、CFD 模擬和Theodorsen理論計算的結果可以看出，ARMA 模型對樣本工況的氣動力遲滯回線與CFD 計算結果基本吻合.同時Theodorsen理論計算結果與兩者的差別很小，說明CFD 計算結果與理論計算結果吻合良好.由于Theodorsen理論計算是在氣體不可壓縮的假設下建立的，而CFD 計算需要大量計算成本，所以采用ARMA 模型在計算成本較低的前提下獲得滿意的動態氣動載荷預測精度就具有普適性的優勢.

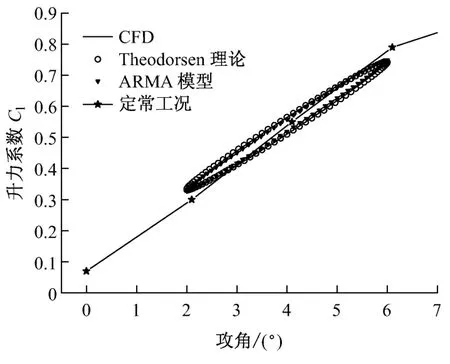
圖2 不同模型的升力系數預測Fig.2 Lift coefficient predicted by different models

采用所建ARMA 模型對其他工況的非定常氣動載荷進行預測，注意攻角的變化范圍應小于靜態失速攻角.圖3給出了ARMA 模型對平均攻角α0＝4°時，振蕩振幅Δα＝2°、1°和衰減頻率k＝0.050、0.060的4個工況以及平均攻角α0＝2°，Δα＝2°時衰減頻率k＝0.050、0.060的2個工況下升力系數的預測結果.從圖3 可以看出，對比CFD 計算結果，ARMA 模型的預測結果十分精確.ARMA 模型在附著流動工況下對非定常氣動載荷有很好的預測能力.

3.2 流動分離工況

當攻角在較大數值（接近或超過靜態失速攻角）處變化時，由于分離的發生，非線性現象得到加強.圖4給出了CFD 計算得出的升力系數在α0＝8°、k＝0.050和Δα＝5.5°時的變化曲線，同時建立Volterra級數模型和ARMA 模型樣本工況進行對比分析.由于過高的記憶長度會提高模型系統辨識的難度，此處選取記憶長度M＝5.從圖4 可以看出，在流動分離工況下，升力系數遲滯回線不再呈橢圓形，這與流動附著時的Theodorsen理論計算結果不同.在翼型上仰階段，失速有被延遲的跡象，而在下俯階段重新附著的過程也存在遲滯.同時，升力系數的遲滯回線出現交叉，說明流動的復雜程度較高.而遲滯回線的閉環明顯要大于附著流動時，說明在流動分離工況下，動態氣動載荷的變化范圍大于附著流動工況.

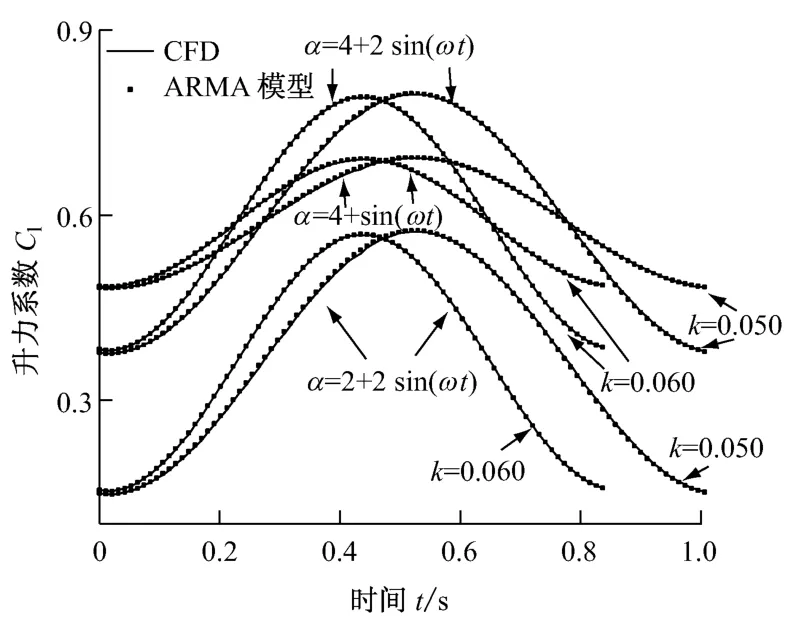
圖3 ARMA 模型對不同工況下升力系數的預測Fig.3 Lift coefficient predicted by ARMA model under different conditions

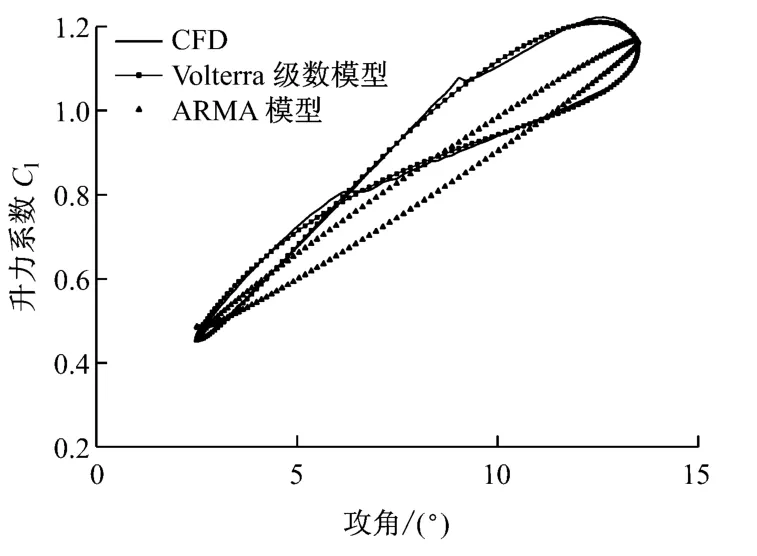
圖4 ARMA 模型和Volterra級數模型的預測對比Fig.4 Comparison of prediction results between ARMA and Volterra series model

在流動分離工況下，ARMA 模型對CFD 計算結果的預測精度大大降低，表明此工況下ARMA模型很難捕捉到響應的實時變化.這是因為ARMA模型只適用于模擬弱非線性的問題，而升力系數在流動分離時的動態響應呈現較高的非線性特征.Volterra級數模型對較強非線性問題的模擬能力高于ARMA 模型，所以從圖4可以看出，Volterra級數模型對于訓練樣本工況的預測與CFD 計算結果吻合更好.采用Volterra級數模型對其他工況進行預測，其結果與CFD 計算結果的對比見圖5.圖中所示的測試工況分別是Δα＝5.5°、10°和k＝0.026，0.050，0.060，0.077的4種組合.由圖5可知，Volterra級數模型對樣本工況以及其他工況除細微差別外整體預測精度很高.說明Volterra級數模型在流動分離工況下可以比較精確地預測翼型所受的非定常氣動載荷.圖4和圖5的計算結果也表明，記憶長度M＝5已經能夠保證模型的精度.

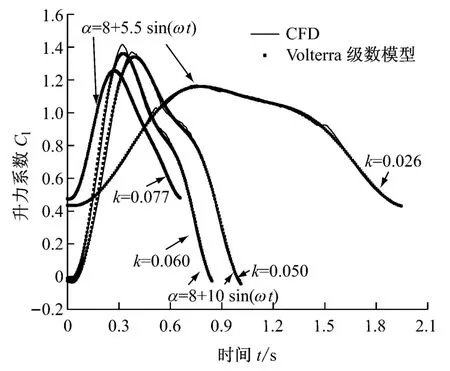
圖5 Volterra級數模型對不同工況下升力系數的預測Fig.5 Lift coefficient predicted by Volterra series model under different conditions

4 結 論

（1）ARMA 模型在流動附著工況下可以很好地預測翼型非定常氣動載荷的變化，但在流動分離工況下其預測能力較差.

（2）Volterra級數模型在流動分離工況下的預測能力較ARMA 模型有了很大提高.其對非定常氣動載荷的預測結果與CFD 計算結果吻合較好，相比具有較高的精度.

（3）采用ARMA 模型和Volterra級數模型預測各自適應工況的非定常氣動載荷是可行的.由于ARMA 模型和Volterra級數模型只需要一個工況的CFD 計算數據作為樣本去辨識各自的模型待定參數，而一旦辨識好后只需幾秒時間就可預測其他工況的非定常氣動載荷.因此，這2種只需較小計算成本的降階模型為非定常氣動載荷的預測、相關的氣動彈性分析以及風力機葉片的設計和優化提供了一種有效的方法.

［1］LEISHMAN J G，NGUYEN K Q.State-space representation of unsteady airfoil behavior［J］.AIAA Journal，1990，28（5）：836-844.

［2］HANSEN MOL.Aerodynamics of wind turbines［M］.London，UK：Earthscan，2008.

［3］劉雄，馬新穩，沈世，等.風力機柔性葉片振動變形對其氣動阻尼的影響分析［J］.空氣動力學學報，2013，31（3）：407-412.

LIU Xiong，MA Xinwen，SHEN Shi，etal.Analysis of the influence of vibration and deformation of the blade on the aerodynamic damping［J］.Acta Aerodynamica Sinica，2013，31（3）：407-412.

［4］俞國華.水平軸風力機葉片失速問題研究［D］.上海：上海交通大學，2013.

［5］周正，李春.風力機翼型等速上仰動態失速數值模擬［J］.能源研究與信息，2013，29（4）：196-200.

ZHOU Zheng，LI Chun.Numerical simulation of identical pitching wind turbine airfoil dynamic stall［J］.Energy Research and Information，2013，29（4）：196-200.

［6］楊錫運，孫翰墨.基于時間序列模型的風電場風速預測研究［J］.動力工程學報，2011，31（3）：203-208.

YANG Xiyun，SUN Hanmo.Wind speed prediction in wind farms based on time series model［J］.Journal of Chinese Society of Power Engineering，2011，31（3）：203-208.

［7］徐敏，陳剛，陳士櫓，等.基于非定常氣動力低階模型的氣動彈性主動控制律設計［J］.西北工業大學學報，2005，22（6）：748-752.

XU Min，CHEN Gang，CHEN Shilu，etal.Design method of active control law based on reduced order model of unsteady aerodynamics for aeroelasticity［J］.Journal of Northwestern Polytechnical University，2005，22（6）：748-752.