消除復合拋物面聚光器二次反射的設計研究

謝胡凌，魏進家，高 陽，趙 亮

（西安交通大學動力工程多相流國家重點實驗室，西安710049）

復合拋物面聚光器（CPC）是一種基于邊緣光學原理設計而成的非成像太陽能聚光器，適用于聚光比為2～10的低聚光比范圍，在跟蹤精度不高的情況下，可有效采集并匯聚太陽能［1］.平板接收型CPC的接收器布置于CPC 出光孔，支撐構件設置在CPC 外側，可保證CPC 聚光光線不受任何部件阻擋，CPC 和接收器組裝便捷且緊湊.因此，在低聚光比范圍內，平板接收型CPC適用于低精度間歇跟蹤的太陽能熱電聯產系統（PV／T）.

將平板接收型CPC應用到PV／T，需解決經濟性和聚光均勻性問題.經濟性方面，隨著CPC 幾何聚光比增加，CPC 高度增加，經濟性變差；聚光均勻性方面，CPC聚光產生的二次反射導致聚光后局部光強過高，使得光伏電池產生熱斑效應，光電轉換效率降低，光伏電池壽命縮短［2］.將CPC 截短可解決上述問題，傳統截短法根據CPC上部反光板反射效果較差的光學特點，截取掉上部CPC，截取比2／3～1／2時認為是比較理想的［3-5］，截取比為截短后的CPC高度與原CPC 高度之比.傳統截短法改善了CPC的經濟性，但并未完全消除二次反射，聚光均勻性不好.為提高CPC 的經濟性和聚光均勻性，筆者提出消除CPC二次反射的設計方法，對此法截短CPC與未截短的CPC、1／2截短CPC的經濟性和聚光均勻性進行對比分析.分析過程中，不考慮CPC制造和安裝誤差.

1 CPC聚光原理與最佳均勻面

1.1 CPC聚光原理

CPC聚光原理如圖1所示，在直角坐標系xoy中，F為拋物線GB的焦點且為拋物線ⅠF下端點，F′為拋物線GB的頂點，為拋物線GB的焦距，拋物線GB和ⅠF以y軸對稱，GⅠ為CPC 入射光孔，BF為CPC出射光孔，θ為CPC 采光半角，H為CPC的高度，CPC 的幾何聚光比CG＝＝1／sinθ.根據邊緣光學原理［6-7］，出射光孔BF左右邊緣有強光匯聚，若入射光線與y軸夾角小于θ，能被CPC匯聚到出射光孔BF，若入射光線與y軸夾角大于θ，則被反射回天空.

圖1 CPC聚光原理圖Fig.1 Schematic diagram of CPC light concentration

1.2 CPC最佳均勻面

出射光孔BF聚光均勻性并不好，如圖2（a）所示，根據邊緣光學原理，出射光孔BF左右邊緣有強光匯聚，但可以找出CPC聚光后的最佳均勻面.

對CPC聚光過程進行幾何分析，可找出這個最佳均勻面，如圖2（a）所示，平行于y軸的入射光線經拋物線CB反射后，可較為均勻地匯聚在A1F1上；平行于y軸的入射光線經拋物線GC反射后，將會在拋物線CB上發生二次反射，但必定匯聚在A1F1上，如圖2（b）所示.假設C1處于拋物線CB上，粗直線為C1的切線，D1C1為即將二次反射的光線，其與x軸的夾角（鈍角）必大于MC1與x軸的夾角（垂直），光線D1C1經C1二次反射后與A1F1交于L2點，MC1經C1反射后與A1F1交于L1點，根據反射定律，L2必定處于L1的左側，因此拋物線GC反射的光線必定匯聚在B1F1上，從而獲得聚光均勻性最佳的接收面，CPC 入射光線都匯聚到這個面上.

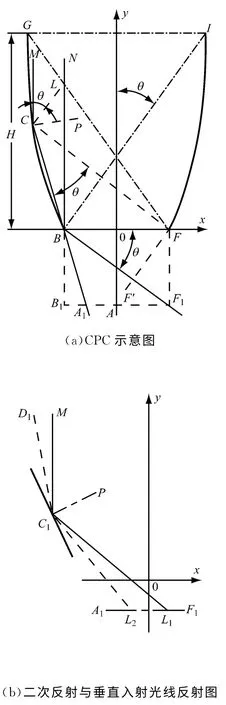
圖2 CPC最佳均勻面示意圖Fig.2 Positioning of the best uniform surface

根據圖2（a）建立的xoy直角坐標系，最佳均勻面B1F1在出射光孔BF下方，與出射光孔BF的距離由式（1）表示：

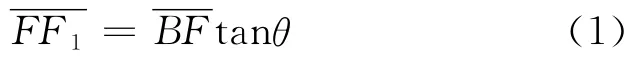
最佳均勻面B1F1寬度與出射光孔BF寬度相等，由式（2）表示：

圖2（a）中的C點為CPC判斷是否有二次反射發生的一個特殊點，光線M-C-B-A1為CPC 是否發生二次反射的特殊光線.

為了進一步驗證最佳均勻面，利用光線追蹤法［8］對CPC進行模擬分析，結果見圖3.如圖3所示最佳均勻面在出射光孔下側，用虛線表示.由圖3（a）可知，出射光孔左右兩側有強光匯聚，最佳均勻面的光強分布更加均勻.圖3（b）給出了CPC 左側拋物線的光線追蹤圖，最佳均勻面上均勻度比出射光孔好，同時可清楚地發現，在最佳均勻面上有密集聚光.將圖3（b）分成兩部分來進行光線追蹤，獲得圖3（c）和圖3（d）的結果，圖3（c）為CPC 發生二次反射光線追蹤圖，在最佳均勻面上有局部高光強區域，由此可知圖3（b）密集聚光由二次反射產生，圖3（d）為未發生二次反射光線追蹤圖，最佳均勻面上從左到右光強逐步增加，均勻度較好，若與右側未發生二次反射光線對稱疊加，均勻度更好.

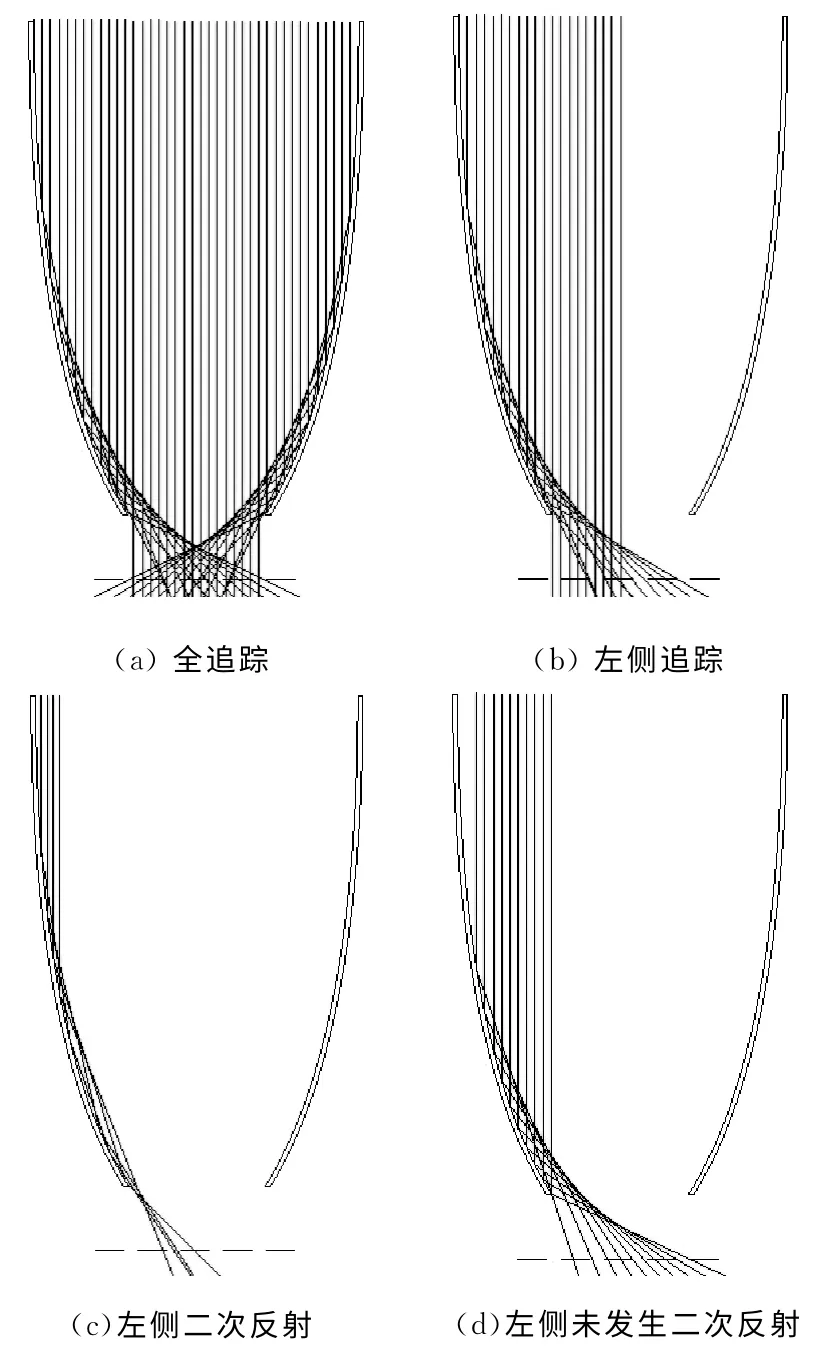
圖3 CPC聚光光線追蹤示意圖Fig.3 Schematic diagram of CPC ray tracing

根據CPC聚光過程幾何分析和光線追蹤分析可知，要分析CPC 聚光后的均勻性，應該分析最佳均勻面處的聚光均勻性.將平板接收型CPC 作為PV／T 的聚光器，應將PV／T 布置到最佳均勻面上.

2 消除CPC二次反射的設計方法

結合傳統截取CPC 的方法，如圖3（c）和圖3（d）所示，將產生二次反射的CPC反射體截取掉，消除二次反射，可顯著提高最佳均勻面上的聚光均勻性，同時提高CPC的經濟性.

根據以上分析，只要找出判斷CPC 是否發生二次反射的特殊光線，相應截取導致二次反射的反射體，就可以提高CPC 聚光的均勻性和經濟性，其原理如圖4所示.圖4中，在xoy直角坐標系中，B1F1為最佳均勻面，H為未截短的CPC 高度，C點為防止CPC產生二次反射的特殊點，M-C-B-A1為特殊光線，H1為消除二次反射設計CPC的高度.

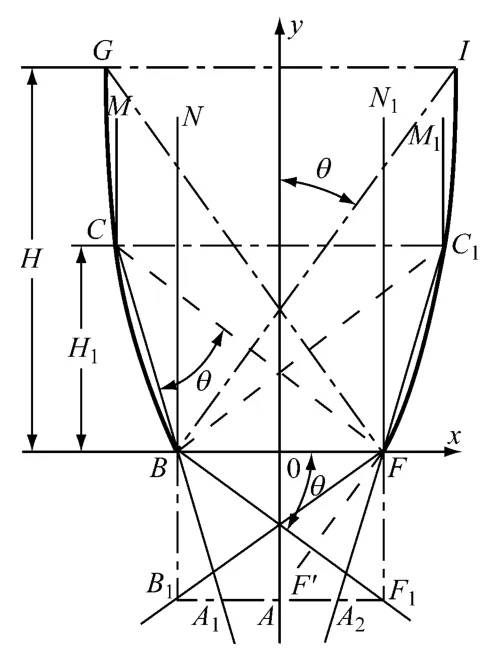
圖4 消除二次反射設計原理圖Fig.4 Schematic diagram of secondary reflection elimination

H1計算方法如下：

（1）對拋物線參數方程進行坐標變換［9］，獲取C點在xoy坐標系中的參數方程組：

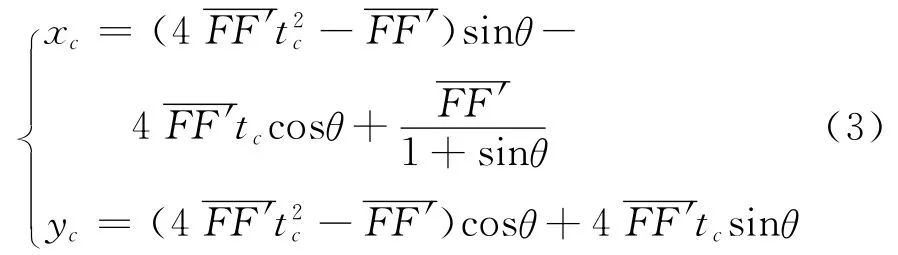
式中：tc為C點在參數方程組中的參數；為拋物線GB的焦距.

根據拋物線焦點到拋物線上任意點之間的距離關系［6-7］，拋物線焦距的表達式為

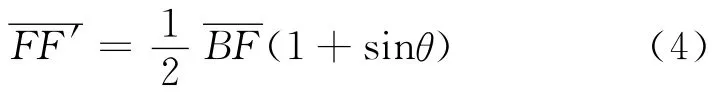
（2）根據∠BCF＝θ這個幾何關系，計算截短后CPC的高度H1，如方程組（5）：

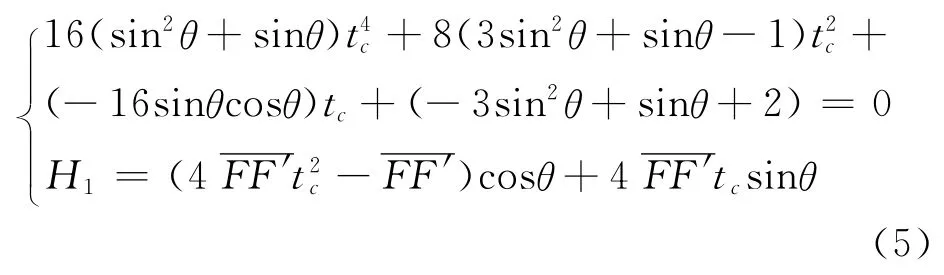
最后，將tc代回特殊點C在xoy坐標系中的參數方程驗算，當滿足xc＜0且yc＞0時，則H1為所求值.

3 消除二次反射設計CPC 的經濟性和聚光均勻性分析

為了分析特殊截短法對CPC 經濟性和聚光均勻性的影響，在相同幾何聚光比下，對比分析未截短的CPC、1／2 截取CPC 和消除二次反射設計CPC的經濟性和聚光均勻性.

首先，在經濟性上對3種CPC各自高度與出射光孔寬度之比進行分析.

（1）原CPC，即未截短的CPC.

高寬比計算公式如下：

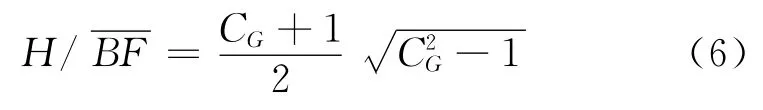
（2）1／2截取CPC.

高寬比計算公式如下：

其中φ與θ1通過如下公式計算［6-7］：

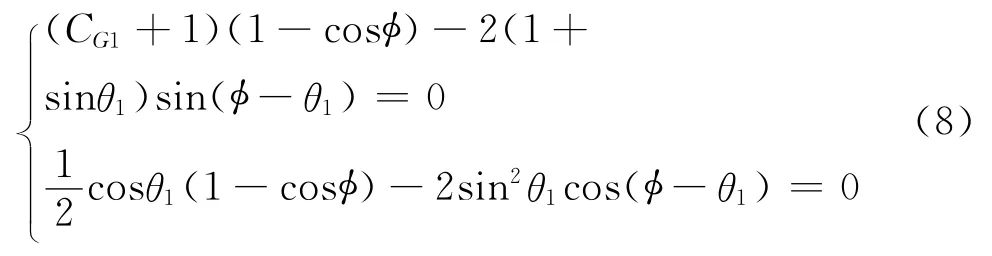
式中：H0為1／2截取CPC 的高度；為出射光孔寬度；CG1為1／2截取CPC 的幾何聚光比；θ1為1／2截取CPC的采光半角.

（3）消除二次反射設計CPC.

高寬比計算公式如下：

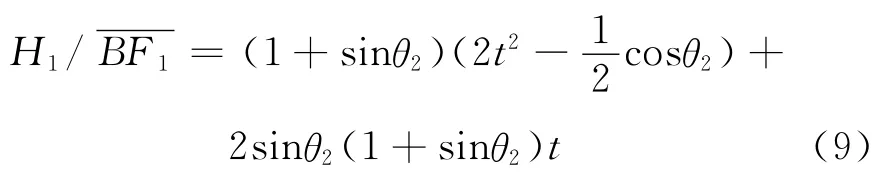
t與θ2通過如下公式計算［6］：

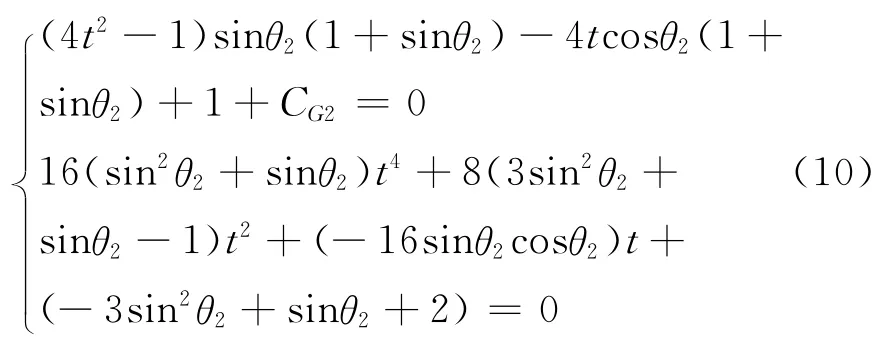
從以上各CPC高寬比的計算公式可以看出，高寬比僅與幾何聚光比有關.

其次，對聚光均勻性進行以下分析.

通過對前述式（1）～式（10）的分析，對于以下尺寸參數：出射光孔與最佳均勻面距離、最佳均勻面寬度、CPC 拋物線上任意點的坐標值、CPC高度、入射光孔寬度、出射光孔寬度，若所有參數均以縮放因子S進行變化，使得CPC以相同縮放因子S進行縮放，CPC采光半角或幾何聚光比不隨尺寸參數變化而變化，因此聚光均勻性不變.聚光均勻性僅與幾何聚光比有關.

3.1 經濟性分析

根據式（6）～式（10）建立數學模型，幾何聚光比選取2～10之間的整數，分別計算未截短的CPC、1／2截取CPC及消除二次反射設計CPC的高寬比，在相同幾何聚光比下對比高寬比，高寬比越小的CPC，經濟性越好.

計算結果如圖5所示，隨著幾何聚光比的增大，未截短的CPC、1／2截取CPC以及消除二次反射設計CPC 的高寬比均增大，未截短的CPC 的高寬比增幅最大，其次為1／2 截取CPC，消除二次反射設計CPC的高寬比增幅最小；對應于每個幾何聚光比，未截短的CPC 的高寬比最大，其次是1／2截取CPC的高寬比，消除二次反射設計CPC 的高寬比最小；幾何聚光比小時，3 種CPC 之間高寬比的差距不大，隨著幾何聚光比增大，3 種CPC 之間高寬比差距越來越大，消除二次反射設計CPC的經濟性更加突出.

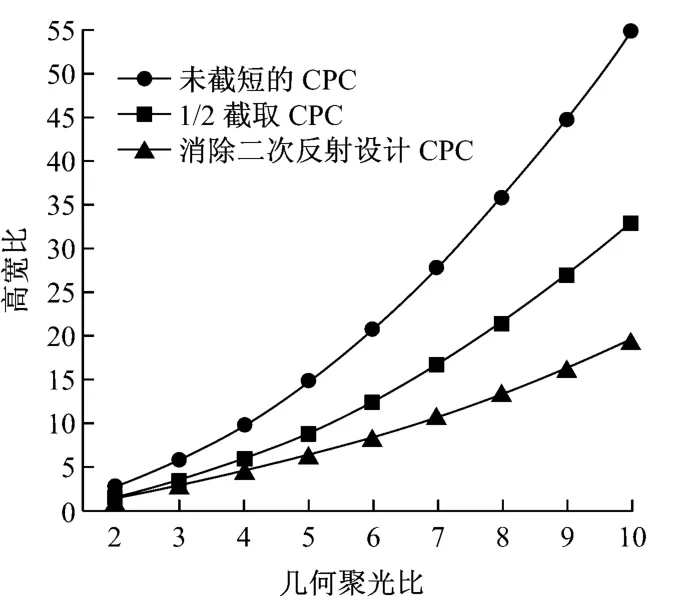
圖5 不同CPC的高寬比隨幾何聚光比的變化Fig.5 Depth-width ratio vs.geometric concentrating ratio of CPCs

3.2 聚光均勻性分析

采用蒙特卡羅法［10］，輻照度為1 000 W／m2，CPC反射率為100%，追蹤光線數量為1 000 000，幾何聚光比為2～10之間的整數，分別計算出未截短的CPC、1／2 截取CPC 以及消除二次反射設計CPC在最佳均勻面上的非均勻度，對比相同幾何聚光比下不同CPC 的非均勻度，非均勻度越小，聚光均勻性越好.

非均勻度參照GB／T 12637—1990《太陽模擬器通用規范》中對光斑非均勻度的計算公式，即非均勻度＝（最大輻照度-最小輻照度）／（最大輻照度＋最小輻照度）.

圖6給出了不同CPC 非均勻度隨幾何聚光比的變化.由圖6可知，隨著幾何聚光比的增大，未截短的CPC、1／2 截取CPC 以及消除二次反射設計CPC的非均勻度均增加，消除二次反射設計CPC的非均勻度增幅最小，當聚光比≥5 時，未截短的CPC和1／2截取CPC的非均勻度幾乎相等；對應于每個幾何聚光比，未截短的CPC 和1／2 截取CPC的非均勻度均大于消除二次反射設計CPC 的非均勻度.因此，消除二次反射設計CPC的非均勻度小，其聚光均勻性比未截短的CPC和1／2截取CPC 的聚光均勻性好.

圖6 不同CPC非均勻度隨幾何聚光比的變化Fig.6 Non-uniformity of concentrated light vs.geometric concentrating ratio of CPCs

將CPC作為PV／T 的聚光器，除了要考慮最佳均勻面上的非均勻度外，還要考慮CPC 聚光后最佳均勻面上的最大輻照度，如果CPC在某幾何聚光比下采用適用同樣幾何聚光比的光伏電池，而此時最佳均勻面上的最大輻照度遠大于該電池正常工作的輻照度，盡管對光伏電池采取冷卻措施，但光伏電池電阻損失將增加，填充因子降低，光電轉換效率降低［2］.因此，聚光后最佳均勻面上的最大輻照度應該盡量接近光伏電池的額定工作輻照度.

在計算CPC 的非均勻度時，獲得不同CPC 最佳均勻面上的最大輻照度與幾何聚光比之間的關系，結果如圖7所示.由圖7可以看出，隨著幾何聚光比的增大，未截短的CPC、1／2 截取CPC 和消除二次反射設計CPC的最大輻照度均增加，但是消除二次反射設計CPC 最大輻照度的增加幅度遠遠小于未截短的CPC和1／2截取CPC，從而使得耦合匹配消除二次反射設計CPC 的光伏電池電阻損失最小，光電轉換效率最高.因此，消除二次反射設計CPC的最大輻照度受到較好的限制，有利于保持光伏電池的光電轉換效率.

圖7 不同CPC最佳均勻面上的最大輻照度與幾何聚光比之間的關系Fig.7 Maximum irradiance on different best uniform surfaces vs.geometric concentrating ratio of CPCs

綜上所述，在幾何聚光比為2～10內，對于未截短的CPC、1／2截取CPC及消除二次反射設計CPC，在相同幾何聚光比下，消除二次反射設計CPC的非均勻度和最大輻照度最小，聚光均勻性最好.

3.3 經濟性和聚光均勻性共同影響分析

根據前述對3種CPC 經濟性和聚光均勻性的分析，可以得出如下結論：幾何聚光比為2～10內，在相同幾何聚光比下，消除二次反射設計CPC 的經濟性和聚光均勻性最好，采用消除二次反射設計CPC可同時在經濟性和聚光均勻性上獲得提高，這對于將CPC應用到PV／T 中具有重要意義.

4 結 論

（1）提出消除CPC 二次反射的設計方法，該設計方法先確定CPC 中是否發生二次反射的特殊光線，再相應截取導致二次反射的反射體，獲得消除二次反射的新CPC.

（2）對未截短的CPC、1／2 截取CPC 以及消除二次反射設計CPC 進行無量綱化，消除CPC 尺寸參數對CPC經濟性和聚光均勻性分析的影響，建立數學模型，根據光線追蹤法和蒙特卡羅法，在幾何聚光比為2～10內，計算CPC高度與出射光孔寬度的比值，并依據該值分析CPC的經濟性，計算CPC 最佳均勻面上的非均勻度和最大輻照度，并依據該值分析CPC 的聚光均勻性，進而對3 種CPC 的經濟性和聚光均勻性進行了對比分析.結果表明，在相同幾何聚光比下，消除二次反射設計CPC 的經濟性和聚光均勻性最好.

［1］KHONKAR H E I，SAYIGH A A M.Optimization of the tubular absorber using a compound parabolic concentrator［J］.Renewable Energy，1995，6（1）：17-21.

［2］WENHAM S R，GREEN M A，WATT M E，etal.Applied photovoltaics［M］.UK：Earthscan，2007.

［3］CARVALHO M J，COLLARES P M，GORDON J M，etal.Truncation of CPC solar collectors and its effect on energy collection［J］.Solar Energy，1985，35（5）：393-399.

［4］劉靈芝，李戩洪.復合拋物面聚光器（CPC）光學分析研究［J］.能源技術，2006，27（2）：52-59.

LIU Lingzhi，LI Jihong.The optical performance of compound parabolic concentrators（CPC）［J］.Energy Technology，2006，27（2）：52-59.

［5］馬鳴，鄭宏飛，李家春.復合拋物面聚光器（CPC）截短對其性能的影響［J］.太陽能，2011（7）：33-36.

MA Ming，ZHENG Hongfei，LI Jiachun.The influence of truncation method on CPC＇s performance［J］.Solar Eneryg，2011（7）：33-36.

［6］WINSTON R，MI?ANO J C，BENíTEZ P.Nonimagin optics［M］.San Diego，California，USA：Elsevier Academic Press，2005.

［7］劉鑒民.太陽能利用：原理·技術·工程［M］.北京：電子工業出版社，2010.

［8］李臻，史月艷，王毓琰，等.具有鏡面反射和漫反射的CPC光學分析［J］.太陽能學報，2003，24（1）：58-63.

LI Zhen，SHI Yueyan，WANG Yuyan，etal.The optical analysis of mirror and diffuse reflection CPC［J］.Acta Energiae Solaris Sinica，2003，24（1）：58-63.

［9］劉連璞.平面解析幾何方法與研究［M］.北京：北京大學出版社，1999.

［10］韋彪，朱天宇.DSG 太陽能槽式集熱器聚光特性模擬［J］.動力工程學報，2011，31（10）：773-778.

WEI Biao，ZHU Tianyu.Simulation on concentrating characteristics of DSG parabolic trough collectors［J］.Journal of Chinese Society of Power Engineering，2011，31（10）：773-778.