如何提升數學的教學效果
邵 娟
(江蘇省淮安市文通中學)
一、想方設法提高學生的積極性
面對數學當中提出的新觀念“幾何直觀”,我們可以通過幾何的觀點去看待。面對這種新鮮的解決數學難題的方法,我們會發現許多難題可以通過教學得到解決。在做證明的時候,我們以往的方式是通過文字的思維去做出分析、做出判斷。現在我們有了“幾何直觀”的新觀念,可以通過圓規直尺更加清晰地畫出圖形來進行分析。這樣我們在見證幾何難題的時候,能更好地得到幾何難題的答案來。讓我們通過幾何畫圖的方式,對幾何難題能做出更好的預判。幾何圖形可以讓我們更好地直接預算出結果來,讓我們在圖畫中明白這道難題的最終結果。這在以前,我們是想象不到的。以前面對一個幾何難題的時候,我們都是運用公式去見證,通過函數的公式去進行分析、去進行解決,現在我們有了“幾何直觀”畫圖的概念,就能更好地解決幾何中的難題。在實際運用當中,我們可以通過數學當中的幾何圖形更好地去分析難題,更好地得到最終的預判結果。面對“幾何直觀”的新概念,我們應該在實際的解決數學難題當中去見證。有了數學“幾何直觀”來解決數學難題,教師可以通過最生動的圖畫就能讓數學中的幾何難題得到解決,而學生也能在幾何難題中更加直觀地知道難題的解決方式。這樣學生在數學教學中更加有興趣,教師也能更好地在課堂中講學。學生的積極性提高了,教師上的數學幾何題也生動有趣了。
二、設計數學上課場景
學習對稱圖形,針對“幾何直觀意識和能力的培養”設計上課場景。
1.題目類型
對稱圖形章節重點和難點知識,結合對稱點求兩點間最短距離。
2.做題技巧
配合圖形,用作圖引出解題思路,形成解題答案。
3.方法優點
便于理解,達到一次理解,長時間不忘,并能靈活運用。
4.題目
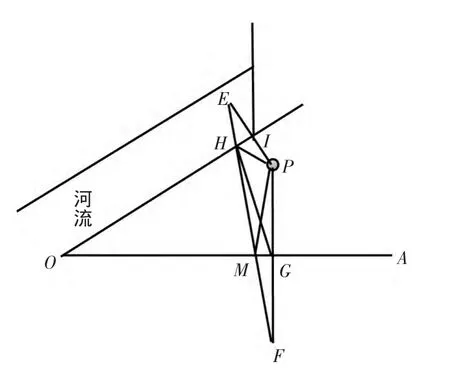
如下圖,一個人從點P出發,到條形草地OA處讓馬吃草,然后到河流OB處讓馬喝水,最后回到點P處,他該怎么走行程才能最短?
5.解題分析
這類題型通過作圖、看圖更能直觀得到解題思路和解題辦法。
6.解題過程
同學們,要找到從點P到OA再到OB后回到點P的最短路徑,我們作圖如上:
如圖,分別做出點P以OA、OB為對稱軸的對稱點F、E,并交OA、OB于點G、I,連接FE交OA、OB于點M、H。連接PM和PH,則最短路徑從點P到點M再到點H最后回到點P,即:PM+MH+HP。
7.原因分析
由對稱點性質得MF=MP,HE=HP,則可以將馬要走的路徑△PMH展開為一條直線EF。由兩點間直線距離最短得到直線EF為最短距離。
8.疑問分析
同學們是不是要提出疑問了,不是點到直線間距離,垂線段距離最短嗎?那最短距離應該是PG+GI+IP呀!下面我們還結合圖形還分析,從圖中我們可以看出,在△HGF中,PG+HG=HG+GF>HF=PM+MH。而由于點I的位置關系,GI>HG。同理在△EIM中,PI+IM=EI+IM>EM=EH+HM。而由于點I的位置關系,GI>IM。
根據圖形可見,走△PMH距離最短。
同學們,是不是通過作圖分析這樣的題型,更有利于我們輕松找到解題思路和解題辦法,更便于記憶,更有利于我們找到快速有效的學習方法。
總之,在教學過程中,促進學生對知識充滿好奇心,對新舊知識能更好地融會貫通,對新知識能更快地消化吸收,讓學生學起來不感覺吃力,使課堂上有其樂融融的學習情境,使學生能形成良好的思維習慣、應用意識和探索數學的能力與精神,讓他們的數學素質不斷提升。

