含泥沙的流固層狀介質(zhì)界面波傳播特性研究

毛志斌，韓慶邦，范洪輝，殷澄，李建，朱昌平

?

含泥沙的流固層狀介質(zhì)界面波傳播特性研究

毛志斌1，韓慶邦1，2，范洪輝3，殷澄1，李建2，朱昌平1

(1. 河海大學(xué)物聯(lián)網(wǎng)學(xué)院，江蘇常州 213022；2. 河海大學(xué)淮安研究院，江蘇淮安 223001； 3. 江蘇理工學(xué)院計(jì)算機(jī)工程學(xué)院，江蘇常州 213001)

在彈性波傳播理論的基礎(chǔ)上，結(jié)合邊界條件，導(dǎo)出了流固層狀介質(zhì)導(dǎo)波特征方程，計(jì)算特征方程的頻散曲線；然后結(jié)合Urick、Urick-Ament和Harker-Temple這三種懸濁液模型，計(jì)算流體層中的泥沙含量和顆粒粒徑與界面波波速的關(guān)系；分析比較不同模型下泥沙含量及顆粒粒徑與波速的關(guān)系圖，討論不同參數(shù)對(duì)波速的影響，得出了三種模型下波速隨泥沙含量和顆粒粒徑的變化趨勢(shì)，最后發(fā)現(xiàn)Urick-Ament模型同時(shí)適用于檢測(cè)懸濁液的泥沙含量和泥沙顆粒粒徑，且在三種模型中有相對(duì)較好的可靠性和實(shí)用性。

層狀介質(zhì)；界面波；頻散曲線；懸濁液模型；泥沙含量；顆粒粒徑

0 引言

對(duì)于河流泥沙含量和顆粒粒徑[1]的檢測(cè)一直是世界范圍的難題，在實(shí)際測(cè)量中會(huì)遇到精度不高、測(cè)量周期過長(zhǎng)、測(cè)量范圍不大等問題。為解決這些問題，之前有人利用聲學(xué)方法進(jìn)行測(cè)量，取得了一定的效果，但是利用界面波[2]檢測(cè)的方法還比較少，本文將著重研究利用界面波檢測(cè)懸濁液泥沙含量和顆粒粒徑的方法。

界面波是指沿著介質(zhì)間交界面?zhèn)鞑サ牟ǎ淠芰恐饕性陔x界面一個(gè)波長(zhǎng)的范圍內(nèi)，且對(duì)兩側(cè)介質(zhì)屬性敏感。早在1924年Scholte就建立了沿流固介質(zhì)交界面?zhèn)鞑サ慕缑娌ɡ碚摚覀兎Q之為Scholte波[3,4]。目前對(duì)Scholte波的應(yīng)用基本集中在固體側(cè)介質(zhì)的屬性研究(如無(wú)損檢測(cè))，而利用界面波反演流體側(cè)介質(zhì)屬性的研究還很少。

關(guān)于泥沙懸濁液模型的研究，在1948年，Urick便提出了第一個(gè)理想狀態(tài)下的模型——Urick模型[5]；之后Ament等人考慮了入射波、折射波、反射波以及散射的復(fù)雜情況，提出了一個(gè)關(guān)系到真實(shí)流體傳播波數(shù)的Urick-Ament模型[6]；隨后Harker和Temple從水動(dòng)力學(xué)的觀點(diǎn)推導(dǎo)了相間相互作用的粘滯阻力方程，提出了耦合相概念的Harker- Temple模型[7]。

本文在流固界面波理論[8]的基礎(chǔ)上，結(jié)合三種泥沙懸濁液模型[9,10]，研究及分析在不同模型下泥沙含量及顆粒粒徑對(duì)界面波波速的影響，從而可以在實(shí)際應(yīng)用中通過實(shí)測(cè)波速和理論關(guān)系曲線來(lái)反推懸濁液中的泥沙含量及顆粒粒徑。

1 界面波特征方程的建立

圖1為層狀介質(zhì)理論模型。以三層介質(zhì)為例，分別為流體層、固體層和半無(wú)限固體層。表示流體層與固體層的交界面，界面波在處沿+方向傳播。

關(guān)于此模型的位移勢(shì)函數(shù)可表示為

；

；

；

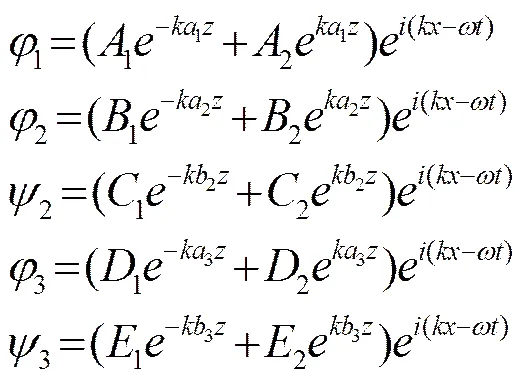
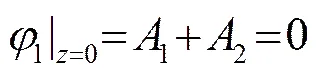
即(2)

半無(wú)限固體介質(zhì)層滿足無(wú)窮遠(yuǎn)處輻射條件，因此：

介質(zhì)中位移及應(yīng)力用位移勢(shì)函數(shù)表示為

；

；

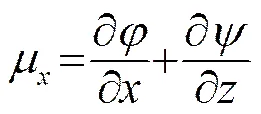
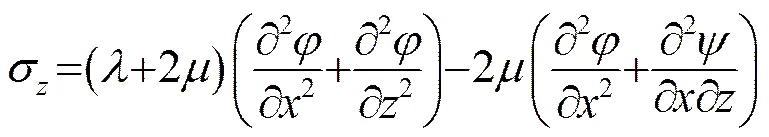
2 界面波頻散計(jì)算

對(duì)于上述含液層的三層介質(zhì)的情況，各層的物理參數(shù)的取值如表1所示。

將表1的參數(shù)代入界面波特征方程，整理計(jì)算得到如圖2所示的圖形。由圖中波速和頻率的關(guān)系，表明界面波具有頻散特性。在聲源頻率小于30 kHz時(shí)只有第一階模式存在，大于30 kHz后會(huì)出現(xiàn)多階模式。對(duì)于第一階模式界面波，當(dāng)聲源頻率接近0 Hz時(shí)，界面波波速接近于第二層介質(zhì)的Rayleigh表面波波速，隨著頻率增加波速慢慢減小且趨于穩(wěn)定，當(dāng)頻率高于50 kHz時(shí)，第一階界面波速度與頻率關(guān)系不大。

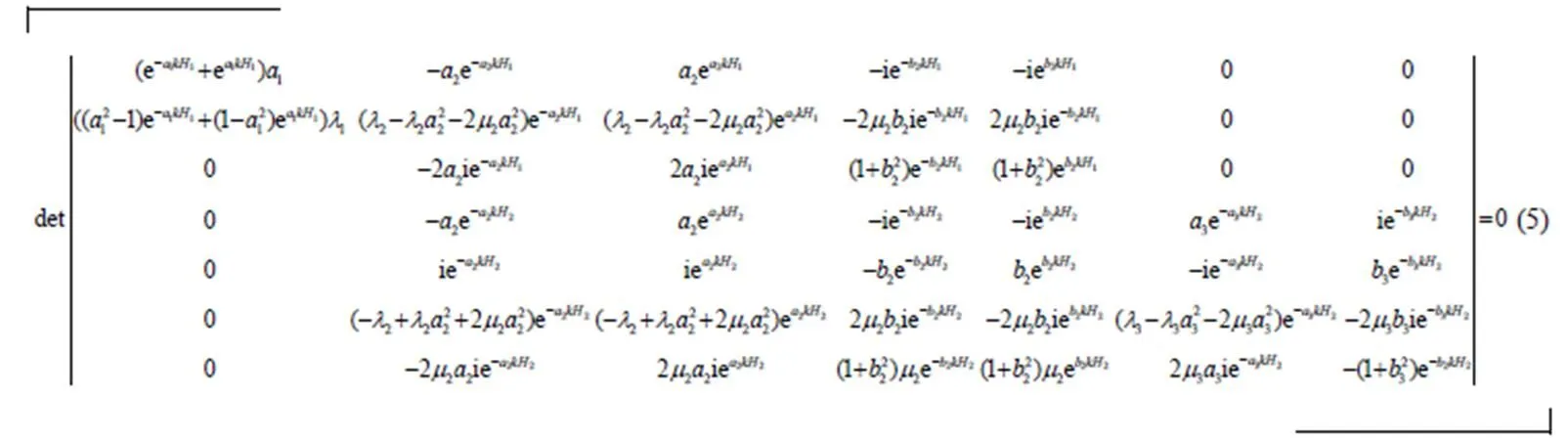
表1 三層介質(zhì)的基本物理參數(shù)

為了比較不同層數(shù)的層狀介質(zhì)界面波頻散特性，這里加入一組兩層介質(zhì)的模型作為比較對(duì)象，其中兩層介質(zhì)的各層物理參數(shù)如表2所示。

圖3給出了兩層層狀介質(zhì)界面波波速與頻率的關(guān)系，從圖中可以看出兩層層狀介質(zhì)的界面波同樣具有頻散特性。為了更好地比較兩層和三層層狀介質(zhì)的界面波頻散特性，將兩種情況的第一階界面波繪于同一幅圖中，如圖4所示。這兩種情況下第一階界面波均是在接近0 Hz時(shí)波速接近Rayleigh波波速，隨著頻率的增加波速逐漸減小且取向穩(wěn)定。同時(shí)，發(fā)現(xiàn)三層介質(zhì)下界面波的頻散截止頻率高于兩層介質(zhì)下界面波的頻散截止頻率。

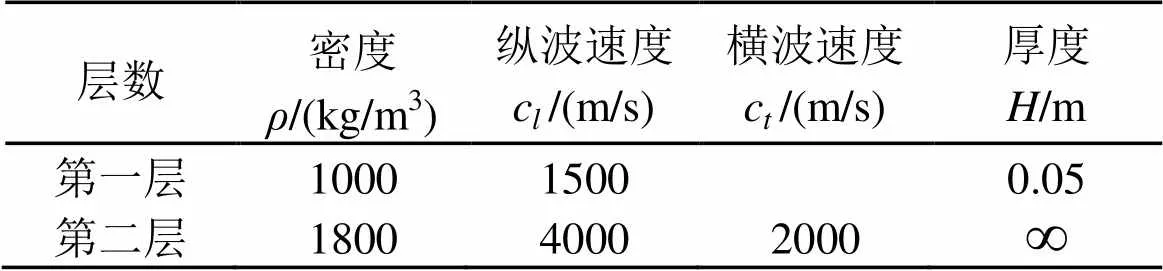
表2 兩層介質(zhì)的基本物理參數(shù)

3 懸濁液理論模型的選取

界面波方法測(cè)量層狀介質(zhì)流體側(cè)泥沙體積含量和顆粒粒徑是通過測(cè)量界面波波速隨流體側(cè)介質(zhì)參數(shù)的變化趨勢(shì)，這一過程中，如何通過數(shù)學(xué)模型準(zhǔn)確、快速地建立界面波波速和物理參數(shù)的關(guān)系尤為重要。為了研究懸濁液中的聲學(xué)特性，研究者已先后提出了一系列數(shù)學(xué)模型[5-7]。

3.1 Urick模型[5]

Urick模型是最早期的關(guān)于超聲波在懸浮液中的傳播波速的模型。在懸浮流體中，將超聲傳播速度以等效密度和等效體積壓縮系數(shù)來(lái)表示：

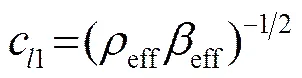
對(duì)于此模型，只需將特征方程的液體密度用等效密度表達(dá)式代替即可得出懸濁液泥沙含量和波速的關(guān)系式。

3.2 Urick-Ament模型[6]

Urick-Ament模型是一個(gè)關(guān)系到真實(shí)流體傳播波數(shù)的復(fù)傳播方程，其中考慮到了入射波、折射波、反射波以及散射的復(fù)雜情況，其方程表達(dá)式為

3.3 Harker-Temple模型[8]

Harker和Temple從水動(dòng)力學(xué)的觀點(diǎn)考慮懸濁液中的生波動(dòng)現(xiàn)象，推導(dǎo)出了相同相互作用的黏性阻力方程，以及每一相獨(dú)立的動(dòng)量和質(zhì)量守恒方程。對(duì)這些微分方程同時(shí)求解可以得出復(fù)波數(shù)方程，即

(9)

4 結(jié)果分析與比較

采用上述三層介質(zhì)中的硬河底，第二層和第三層介質(zhì)的物理參數(shù)如表1所示。流體層(第一層介質(zhì))為泥沙懸濁液，不考慮泥沙的沉積作用，認(rèn)為泥沙顆粒大小一致且分布均勻，表3為泥沙懸濁液相關(guān)介質(zhì)的參數(shù)表。

表3 泥沙懸濁液的相關(guān)介質(zhì)參數(shù)表

圖5是上述條件時(shí)，三種模型下懸濁液泥沙含量與界面波波速的關(guān)系曲線對(duì)比圖。本組計(jì)算中，數(shù)值仿真了頻率為50 kHz、粒徑為60、懸濁液泥沙含量從0%增加到20%時(shí)各模型對(duì)應(yīng)界面波波速的變化趨勢(shì)。從圖中可以清楚地看出，對(duì)于Urick模型，隨著懸濁液泥沙體積含量的增加，界面波波速呈現(xiàn)逐漸減小的趨勢(shì)；而對(duì)于Urick- Ament模型和Harker-Temple模型，隨著泥沙體積含量的增加，界面波波速都呈現(xiàn)增大的趨勢(shì)，且Urick-Ament模型的增大趨勢(shì)比Harker-Temple模型更加明顯，說明它對(duì)泥沙濃度更加敏感，在實(shí)際應(yīng)用中使用此模型能得到更好的效果。

圖6所示是三種模型下泥沙懸濁液顆粒粒徑與界面波波速的關(guān)系曲線圖。本組計(jì)算數(shù)值仿真了頻率為50 kHz，泥沙體積濃度為12%，懸濁液顆粒粒徑從50增加到100時(shí)各模型對(duì)應(yīng)界面波波速的變化趨勢(shì)。從圖中可以清晰地看出，Urick模型和Harker-Temple模型所對(duì)應(yīng)的速度并不隨顆粒粒徑的改變而發(fā)生改變，這也與兩種模型所對(duì)應(yīng)的方程是一致的。Urick模型的表達(dá)式中并未出現(xiàn)粒徑的量，因此速度不隨粒徑發(fā)生改變；而Harker- Temple模型的表達(dá)式中雖然出現(xiàn)了含粒徑的量，但是它出現(xiàn)在了表達(dá)式的虛部，根據(jù)物理意義可以知道粒徑對(duì)聲波的衰減影響較大，而對(duì)速度的影響非常小，有時(shí)可以將其忽略。對(duì)于Urick-Ament模型，速度隨著顆粒粒徑的增加呈現(xiàn)增大的趨勢(shì)，更加符合實(shí)際情況。

結(jié)合上述兩種分析比較，界面波在傳播時(shí)具有一定規(guī)律，它的傳播速度和懸濁液的體積濃度及泥沙的顆粒粒徑具有一定的對(duì)應(yīng)關(guān)系。在討論上述三種模型時(shí)，結(jié)合實(shí)際我們發(fā)現(xiàn)，當(dāng)檢測(cè)懸濁液顆粒相體積含量時(shí)，Urick-Ament模型和Harker-Temple模型具有較強(qiáng)的實(shí)用性；而當(dāng)檢測(cè)顆粒粒徑時(shí)，Urick-Ament模型的實(shí)用性是三種模型中最強(qiáng)的。綜上所述，對(duì)于上述三種模型，在同時(shí)進(jìn)行體積濃度和顆粒粒徑檢測(cè)時(shí)，Urick-Ament模型更加貼近實(shí)際，有更好的實(shí)用性。

5 結(jié)語(yǔ)

本文將流固層狀介質(zhì)界面波特征方程與泥沙懸濁液聲傳播模型相結(jié)合，首先對(duì)比了兩層和三層介質(zhì)界面波的頻散特性，隨后基于Urick模型、Urick-Ament模型和Harker-Temple模型這三種懸濁液模型分析了層狀介質(zhì)流體側(cè)介質(zhì)屬性對(duì)界面波波速的影響，結(jié)果說明在同時(shí)適用對(duì)泥沙體積含量和顆粒粒徑的檢測(cè)時(shí)，Urick-Ament模型是相對(duì)合適的模型。所得結(jié)論將為以后用界面波方法對(duì)河流中泥沙體積含量和泥沙顆粒相粒徑的檢測(cè)提供理論依據(jù)。

[1] 侯懷書, 張鎖懷. 基于中低頻超聲波的納米顆粒粒徑測(cè)量[J]. 機(jī)械工程材料, 2011, 35(5): 80-82.

HOU Huaishu, ZHANG Suohuai. Nanoparticle-based particle size measurement of low-frequency ultrasound[J]. Materials for Mechanical Engineering, 2011, 35(5): 80-82.

[2] 朱哲民, 李劍, 鄒薇.有液層負(fù)載時(shí)薄板中類Lamb波的傳播[J].聲學(xué)學(xué)報(bào), 1996, 21(3): 174-181.

ZHU Zheming, LI Jian, ZOU Wei. The propagation of Lamb waves in sheet with liquid laver[J]. Acta Acustica, 1996, 21(3): 174-181.

[3] M.de Billy, G. Quentin. Experimental study of the Scholte wave propagation on a plane surface partially immersed in a liquid[J]. 1983, 54(8): 4314-4322.

[4] 祝捍皓, 樸勝春, 張海剛. 水平分層彈性海底環(huán)境下Scholte波特性的研究[J]. 聲學(xué)技術(shù), 2011, 30(3): 1576-1588.

ZHU Hanhao, PU Shengchun, ZHANG Haigang. Study on the characteristic of scholte waves in flexible hierarchical level under the seabed environment[J]. Technical Acoustics, 2011, 30(3): 1576-1588.

[5] Urick R J. A sound velocity method for determining the compressibility of finely divided substances(S0021-8979)[J]. J. Appl. Phys, 1947, 18(11): 983-987.

[6] Urick R J, W S Ament J. The propagation of sound in composite-media(S0001-4966)[J]. J. Acoust. Soc. Am., 1949, 21(2): 115.

[7] Harker A H, Temple J A G. Velocity and attenuation of ultrasound in suspensions of particles in fluids[J]. J Phys D: Appl Phys, 1988, 21(11): 1576-1588.

[8] 韓慶邦, 錢夢(mèng)騄, 朱昌平. 激光超聲方法研究固-固界面波傳播特性[J]. 物理學(xué)報(bào), 2001, 56(1): 313-320.

HAN Qingbang, QIAN Menglu, ZHU Cangping. Study on solid-soild interface waves with laser ultrasonics[J]. Acta Physica Sinica, 2001, 56(1): 313-320.

[9] Tebbutt J S, Challis R E. Ultrasound wave propagation in colloidal suspensions and emulsions: a comparison of four models[J].Ultrasonics, 1996, 34(2-5): 363-368.

[10] 蘇明旭, 蔡小舒.超細(xì)顆粒懸濁液中聲衰減和聲速的數(shù)值模擬[J]. 上海理工大學(xué)學(xué)報(bào), 2002, 24(1): 21-25.

SU Mingxu, CAI Xiaoshu. Numerical simulation of ultrafine particle suspension sound attenuation and speed of sound[J]. J. University of Shanghai for Science and Technology, 2002, 24(1): 21-25.

Research on the characteristics of fluid-solid interface wave propagation in layered sediment medium

MAO Zhi-bin1, HAN Qing-bang1,2, FAN Hong-hui3, YIN Cheng1, LI Jian2, ZHU Chang-ping1

(1. Internet of Things EngineeringCollege of Hohai University,College of IOT Engineering Changzhou, Changzhou 213022, Jiangsu,China; 2. Huaian Research Institute of Hohai University, Huai’an223001, Jiangsu,China; 3. School of Computer Engineering, Jiangsu University of Technology, Changzhou 213001, Jiangsu,China)

Based on the theory of elastic wave propagation and boundary conditions, the characteristic equation of fluid-solid interface waves propagation in layered sediment medium is derived; three suspended fluid modelsof Urick, Urick-Ament and Harker-Temple are used to investigate the relations between velocity and sediment concentration as well as particle size.By the discussion of the impact of different parameters on the velocity, the velocity variation trends under three models with the change of sediment concentration and particle size are obtained. As a result, it is found that Urick-Ament model is more applicable to the detection of sediment concentration and sediment suspension particle size for the fluid-solid interface wave.

layered medium; interface waves; dispersion curve; suspension models; sediment concentration; particle size

TB551

A

1000-3630(2015)-03-0198-05

10.3969/j.issn1000-3630.2015.03.002

2014-03-05;

2014-06-05

國(guó)家自然科學(xué)基金(11274091、61302124、11274092), 河海大學(xué)中央高校基金項(xiàng)目(2011B11014), 淮安河海研究生院開放基金資助項(xiàng)目。

毛志斌(1989－), 男, 江蘇蘇州人, 碩士, 研究方向?yàn)橥ㄐ烹娐放c聲學(xué)技術(shù)。

韓慶邦, E-mail: hqb0092@163.com