Ritz法解決一類二階常微分方程

符艷麗，么煥民

(哈爾濱師范大學)

0 引言

二階常微分方程廣泛應用于現實生活及科學工程等各種領域，近年來，更多的被投入到試圖尋找微分方程的有效方法上，如，再生核方法［1－2］，變分法、有限元法和外推法［3］，配置法［4］及各種改進的配置法［5］.特別地，對于配置法，常常選取多項式作為基函數［4］，而針對基函數的選取的不同，解的精確程度也不同.

該文針對一類二階微分方程的邊值問題提出一種Ritz法，并采取不同個數的基函數來說明基函數選取的不同，精確度也會不同，通過數值算例，就可以看出這種比較的優勢所在.

1 Ritz法解決常微分方程問題

該文針對以下的常微分邊值問題給出一種Ritz法，

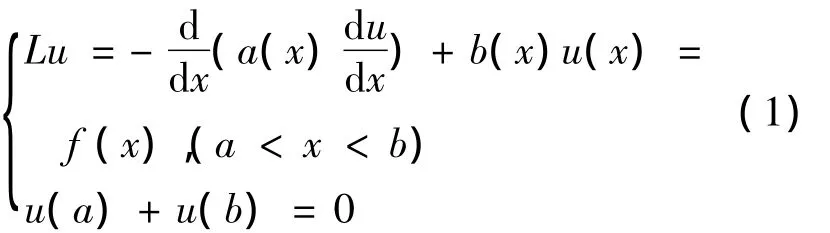
其中a(x)＞0，b(x)≥0且a(x)∈C1［a，b］，b(x)∈C［a，b］.

定義1.1 定義集合［a，b］={f(x)|f(x)∈C2［a，b］，f(a)=f(b)=0}，即將所有在［a，b］在上有二階連續導數且在兩端點為零的函數的集合定義為［a，b］.

定義 1.2 定義內積〈u(x)，v(x)〉 =

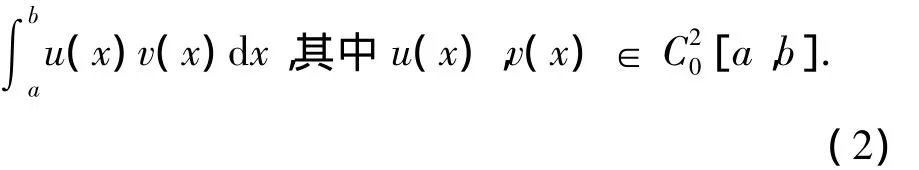
定理1.1 假設u0(x)是方程(1)的解，則u0(x)使泛函R［u(x)］取最小值R［u0(x)］，反之，若u0(x)∈［a，b］使泛函R［u(x)］取最小值R［u0(x)］，則u0(x)是方程(1)的解，其中

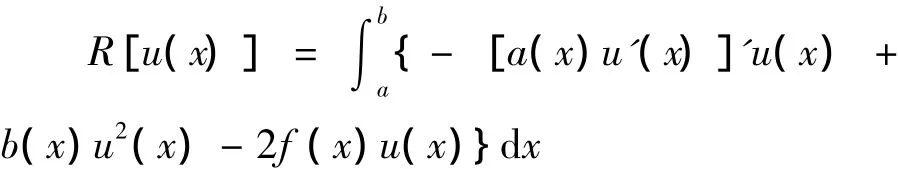
證明 (1)設u0(x)是方程(1)的解，?v(x)∈［a，b］，所以

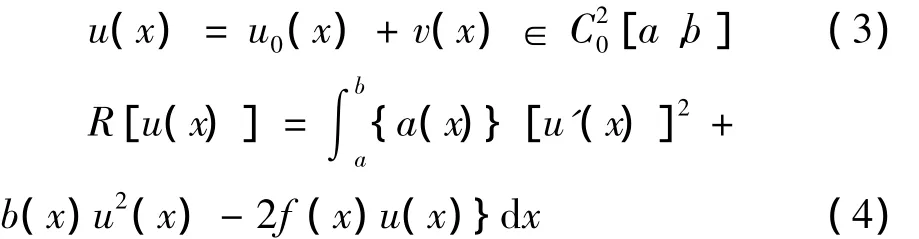
由(3)得

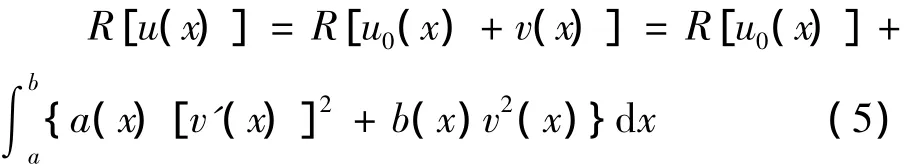
由(1)可知，若v(x)不恒為 0，則(見文獻［3］)，這意味著只要u(x)不恒等于v(x)，那么

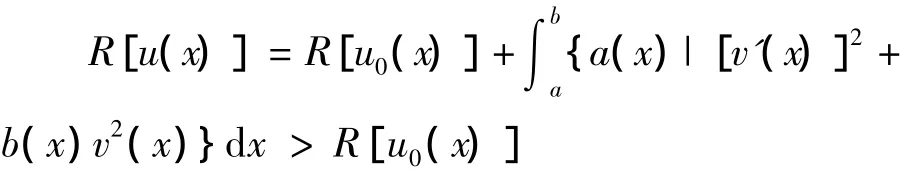
即R［u(x)］在方程(1)下的解u0(x)上達到最小值R［u0(x)］.

(2)假設泛函R［u(x)］在u0(x)上達到最小值R［u0(x)］，對?v(x)∈［a，b］，?λ∈R，有R［u0(x)+λv(x)］=R［u0(x)］+

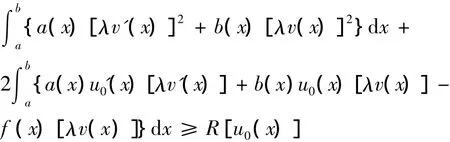
當u0(x)及v(x)固定時，此時上式的后半部分為λ的函數，記為Ψ(λ)，即

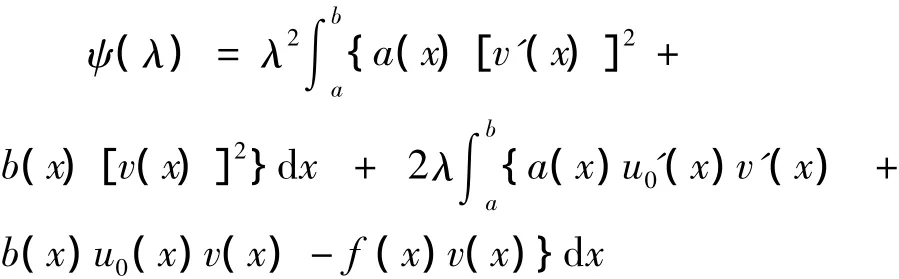
由已知ψ(λ)=aλ2+bλ+c≥0，則Δ=b2–4ac≤0，即b=0.由分部積分有恒成立，那么

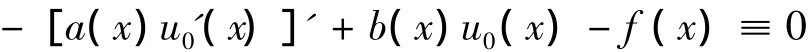
即u0(x)是方程(1)的解(見文獻［3］)，證畢.

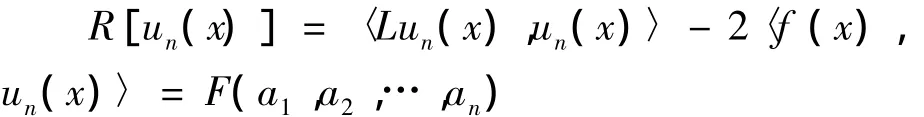
可以把R［un(x)］看成是ai的函數，即此時的ai使R［un(x)］=F(a1，a2，…，an)取最小值.

由于F(a1，a2，…，an)是二次函數，所以此時的最小值就是極小值，令n)，得

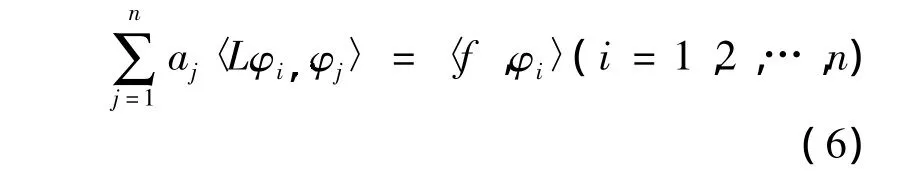
這是以ai(i=1，2，…，n)為變量的n維線性方程組CA=B，解(6)就可以表示出un(x).

下面做一些記號:

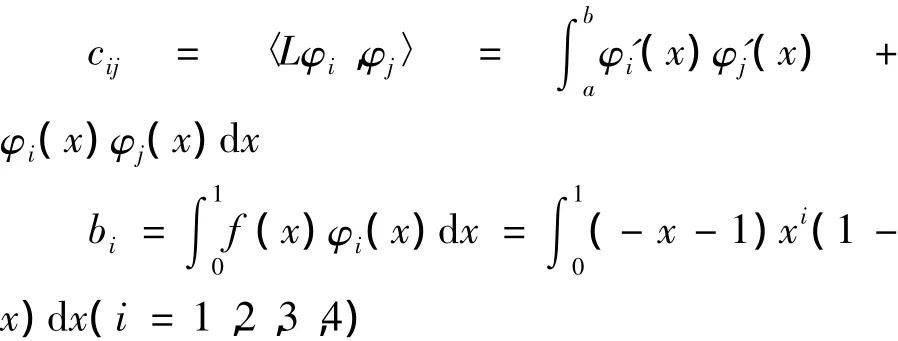
由文獻［2－3］可知方程(1)有唯一解，同時由Ritz法得到的極小化序列{un(x)}平方收斂于方程(1)的精確解u(x).

2 數值算例

令方程(1)中的a(x)=b(x)=1，f(x)=–x－1，即求函數u(x)∈C2［0，1］，使它滿足

此方程的精確解為

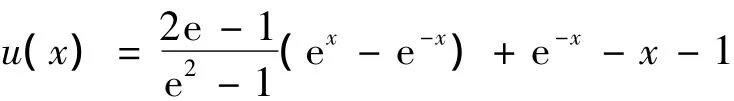
接下來用Ritz法求(7)的近似解un(x)，以資比較，令φi(x)=xi(1–x)(i=1，2，3，4)，顯然φi(0)=φi(1)=0，且φi(x)∈C20［a，b］(i=1，2，3，4)，線性無關，可作為基函數，同時

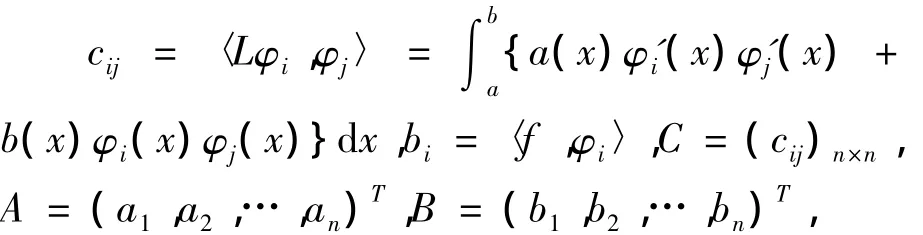
所以，此時得到線性方程組

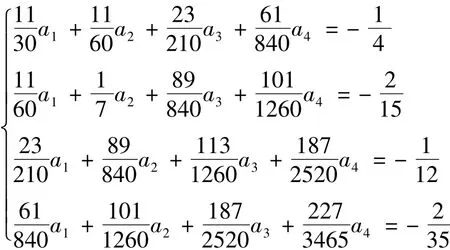
解此方程組得出a1，a2，a3，a4，從而得到近似解

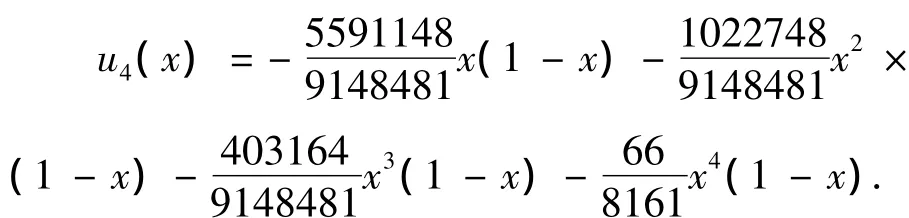
試選點x［0，1］，求得u1.37966×10－6.

現在對［0，1］取十等分點xi=0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1(i=1，2，…，10)，分別求出近似值u4(x)和準確值u(x)，及誤差Δu4(x)并作比較，如表1所示.

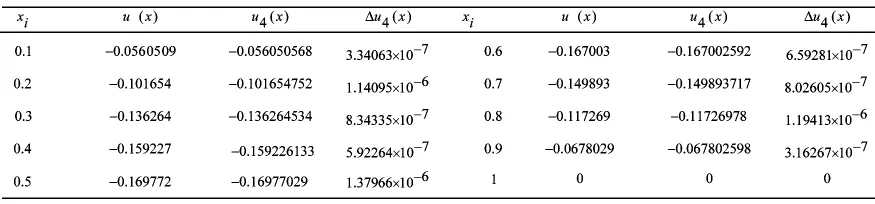
表1

由表1可以看出近似解的誤差Δu4(xi)=u(xi)－u4(xi)，(i=1，2，…，10)已經達到10－7，但文中只取了4個基函數，用同樣的方法可以取更多的基函數來作比較，不難得到收斂速度越來越快的結論.

3 關于Ritz法的幾點說明

(1)使用Ritz法時，對于基函數的選取沒有一定的標準，即針對不同的方程如何選擇基函數才能使誤差最小，收斂速度最快，通常情況下多項式函數是首選，并篩選出最合適的基函數.

(2)使用Ritz法時，即使使用相同的基函數當方程(1)中的f(x)不同時，收斂速度也會不同.

(3)使用Ritz法時，基函數的種類、光滑性、個數不同時，通過文中的研究可以看出方程(1)中近似解與精確解的收斂速度也會不同.

所以，針對不同的方程模型，應該隨機應變地找出合適的基函數，這是完善Ritz法所要做的必要工作，還需要進一步研究.

［1］Li X Y，Wu B Y.Error estimation for the reproducing kernel method to solve linear boundary value problems［J］.Journal of Computational and Applied Mathematics，2013，243:10–15.

［2］吳勃英，林迎珍.應用型再生核空間［M］.北京:科學出版社，2012.

［3］劉詩俊，變分法有限元法和外推法［M］，北京:中國鐵道出版社，1984:64－79.

［4］Russell R D，Shampine L F.A collocation method for boundary value problems［J］.Numerische Mathematic，1972，19:1－28.

［5］Mehdi Dehghan，Ahmad Nikpour.Numerical solution of the system of second－order boundary value problems using the local radial basis functions based differential quadrature collocation method［J］.Applied Mathematical Modelling，2013，37:8578－8599.