數學中考中幾種問題的解決策略

盛愛霞

摘 要： 中考數學中有幾個方面的問題學生丟分嚴重，課堂教學中需專題化解決.本文對存在性問題，數學建模問題，歸納、猜想型問題，動態問題等方面作探討。

關鍵詞： 數學中考 數學問題 解決策略

一、“存在性問題”解題策略

存在性問題是根據已知條件，探索制定適合某個問題的結論的數值、點、直線或其圖形是否存在的題目，常見類型有：（1）等腰三角形存在問題；（2）直角三角形存在問題；（3）平行四邊形存在問題；（4）相似三角形存在問題.在中考中，函數圖像中點的存在問題是重點，其解題思路是：先對結論作出肯定的假設；然后由肯定假設出發，結合已知條件進行正確的計算、推理，若導出矛盾，則否定先前假設；若推出合理的結論，則說明假設正確，由此得出問題的結論.它主要考查考生的觀察、分析、比較、歸納、推理等方面的能力.由于這類題目的綜合性極強，因此中考常以壓軸題出現.幾何與代數相結合的綜合題涵蓋初中階段所學的代數與幾何的重要知識點和多種數學思想方法，特別注意運用數形結合的思想方法溝通幾何與代數知識之間的內在聯系，運用通過數研究形與通過形研究數的解題策略，主要題型為：在坐標系中研究直線型圖形、圓、函數圖像，在直線型圖形和圓中研究幾何變量之間的函數關系，從問題的類型來看主要有探索性問題、存在性問題、開放性問題.

二、“數學建模問題”解題策略

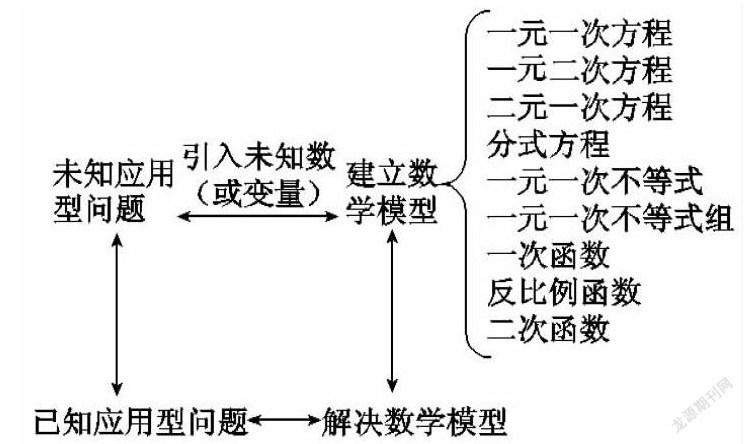
數學應用性問題在近年的數學中考中是每一個省市必考的問題，這類問題的出題率越來越高，題材也越來越廣泛.對這類有實用價值并且應用非常廣泛的問題，通過數學建模的方法一般都可以抽象為數學應用題，因此探究運用建立數學模型的解題思路顯得十分必要，在初中階段通常建立方程模型、不等式模型、函數模型或幾何模型.

三、“歸納、猜想型問題”解題策略

所謂歸納、猜想型問題指的是給出一組具有某種特定關系的數、式、圖形或是給出與圖形有關的操作、變化過程，要求通過觀察、分析、推理、探求其中所蘊含的規律，進而歸納或猜想出一般性的結論，常見的類型有：（1）數式猜想型；（2）圖形規律型；（3）數形結合猜想型.常結合的知識有：數與式的運算、因式分解、不等式的性質、平面直角坐標系、三角形、特殊四邊形、幾何變換圖形的組合等.

解題思想方法：從考慮個別、特殊的對象出發，利用特殊性、特殊數量、特殊點、特殊線段、特殊位置等進行歸納、猜想、概括，從特殊到一般，從而得出規律.

四、“動態問題”解題策略

動態型問題是以點、線、面（如三角形、四邊形）的運動為情境，探索和發現其中規律和結論的中考題型，由于圖形的運動，導致題目的條件不斷改變，隨之相應的數量關系和結論也可能改變.這樣就出現一個事件中蘊含著多個數學問題，既獨立又有聯系，使題目無論從考查知識上，還是解決方法上都具有較強的綜合性，達到培養和考查學生的觀察、試驗、空間想象、分析綜合等解決問題的能力的目的，在全國的中考試卷中常作為壓軸題出現，類型有：（1）點的運動；（2）線的運動；（3）面（如三角形、四邊形）的運動.

解決動態問題的思維與方法：（1）認清問題中的靜態圖形和動態圖形，并確定動態圖形的起始位置和終止位置；（2）畫出不同時刻動態圖形與靜態圖形形成的幾何圖形，這樣就能由“動”變“靜”，再設法分別求解問題.

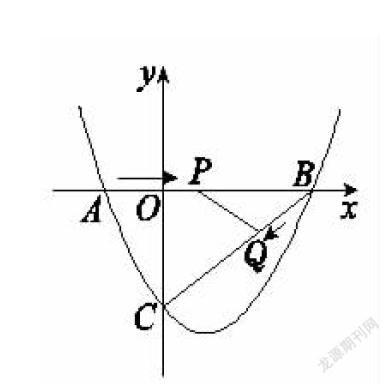
例：如圖，在平面直角坐標系中，拋物線y=ax+bx-3（a≠0）與x軸交于點A（-2，0），B（4，0）兩點，與y軸交于點C.

（1）求拋物線的解析式；

（2）點P從點A出發，在線段AB上以每秒3個單位長度的速度向點B運動，同時點Q從點B出發，在線段BC上以每秒1個單位長度向點C運動.其中一個點到達終點時，另一個點也停止運動.當△PBQ存在時，求運動多少秒使△PBQ的面積最大，最大面積是多少？