生活中的一元二次方程

彭翠紅

我們在學習數學知識的同時，更重要的是學會用數學知識解決生活中的實際問題，這樣才能體現數學的應用價值，下面我們舉幾個與“一元二次方程”相關的實例.

一、 傳播問題

例1 甲型H1N1流感病毒的傳染性極強，某地因1人患了甲型H1N1流感沒有及時隔離治療，經過兩天的傳染后共有9人患了甲型H1N1流感.（1） 平均每天一個人傳染了幾人？（2） 如果按照這個傳染速度，再經過5天的傳染后，這個地區一共將會有多少人患甲型H1N1流感？

【分析】假設平均每天一個人傳染x人，如果前一天只有1個人感染，1天后感染總人數上升為（x+1）人；前一天2個人感染，1天后感染總人數上升為（x+1）+（x+1）=2（x+1）人；前一天有a個人感染，1天后感染總人數上升為a（x+1）人；若前一天（x+1）個人感染，1天后感染總人數上升為（x+1）（x+1）=（x+1）2人.對于例1，1天后感染的總人數是（x+1）人，再過一天后感染總人數上升為（x+1）2人，即兩天后的感染總人數；又過一天感染總人數上升為（x+1）3人，即三天后的感染總人數……；再過5天即7天后的感染總人數為（x+1）7人.

解：（1） 設平均每天一個人傳染了x人，

由題意得：（x+1）2=9，

解這個方程，得：

x1=2，x2=-4（x2=-4不合題意，舍去）.

（2） （x+1）7=37=2 187（人）.

答：（1） 每天平均一個人傳染了2人；（2） 再經過5天的傳染后，這個地區一共將會有2187人患甲型H1N1流感.（可見傳播力量的強大）

練練身手1 某種植物的主干長出若干數目的支干，每個支干又長出同樣數目的小分支，主干、支干和小分支的總數是91，每個支干長出多少小分支？

二、 增長率問題

例2 （2015·甘肅蘭州） 股票每天的漲、跌幅均不超過10%，即當漲了原價的10%后，便不能再漲，叫作漲停；當跌了原價的10%后，便不能再跌，叫作跌停.已知一只股票某天跌停，之后兩天時間又漲回到原價，若這兩天此股票股價的平均增長率為x，則x滿足的方程是（ ）.

A. （x+1）2=11/10 B. （x+1）2=10/9

C. 1+2x=11/10 D. 1+2x=10/9

【分析】本題的難點是跌停前的單價未知，而且單價經歷了跌停，連續兩次增長共三個階段.我們可以假設跌停前的單價為單位1，則跌停后單價為9/10，即第一個階段后的結果；增長1天后的單價為增長前的（x+1）倍，為9/10（1+x），即第二個階段后的總結果；增長2天后是1天后的（x+1）倍，為9/10（x+1）2，即第三個階段后的總結果.因此可得方程：9/10（x+1）2=1，方程兩邊同乘10/9得：（x+1）2=10/9.所以選B.

【點評】無論是流感傳播問題還是增長率的問題，都可以理解為每過一天，數量將是前一天的（1+x）倍，若原始數量是a，則一天后總數量是a（1+x），兩天后總數量是a（1+x）2，三天后總數量是a（1+x）3，……，n天后總數量是a（1+x）n，用乘積的形式表示若干天后的數量比用和的形式要簡潔很多.

三、 利潤問題

例3 百佳超市將進貨單價為40元的商品按50元出售時，能賣500個，已知該商品每漲價1元，其銷售量就要減少10個，為了賺8 000元利潤，售價應定為多少，這時應進貨多少個？

【分析】上述問題中如果銷售價按照單價50元的話，每個利潤是10元，可以賣出500個，共可獲利5 000元，無法完成利潤8 000元的目標，所以只有改變單價并控制適當的單價，才可以完成獲得利潤8 000元的任務.設商品單價為（50+x）元，則每個商品得利潤[（50+x）-40]元，因為每漲價1元，其銷售會減少10，則每個漲價x元，其銷售量會減少10x個，故銷售量為（500-10x）個，根據每件商品的利潤×件數=8 000，則應用（500-10x）·[（50+x）-40]=8 000.

解：設每個商品漲價x元，則銷售價為（50+x）元，銷售量為（500-10x）個，由題意得：（500-10x）·[（50+x）-40]=8 000，

整理得：x2-40x+300=0，

解得：x1=10，x2=30.

經檢驗x1=10，x2=30都符合題意.

當x=10時，50+x=60，500-10x=400；

當x=30時，50+x=80，500-10x=200.

答：要想賺8 000元，售價為60元或80元.若售價為60元，則進貨量應為400個；若售價為80元，則進貨量應為200個.

四、 面積問題

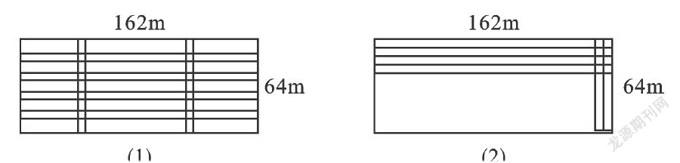
例4 一塊矩形耕地大小尺寸如圖所示，要在這塊土地上沿東西和南北方向分別挖4條和2條小渠，如果小渠的寬相等，而且要保證余下的耕地面積為9 600 m2，那么水渠應挖多寬？

【分析】這類問題的特點是，挖渠所占面積只與挖渠的條數和渠道的寬度有關，而與渠道的位置無關. 為了研究問題方便可分別把東西和南北方向的渠道移動到一起（最好靠一邊），如圖（2）所示.那么剩余可耕的長方形土地的長為（162-2x） m，寬為（64-4x） m；

解：設水渠的寬為x m，由題意得：

（162-2x）（64-4x）=9 600，

解得：x1=1，x2=96（x2=96不合題意，舍去）.

答：水渠的寬為1 m.

練練身手2 （2015·四川自貢）利用一面墻（墻的長度不限），另三邊用58 m長的籬笆圍成一個面積為200 m2的矩形場地.求矩形的長和寬.

參考答案

練練身手1：

解：設每個支干長出x個小分支，則主干數量為1，支干數量為x，小分支數量為x2，由題意得：1+x+x2=91，

解得：x1=-10，x2=9（x1=-10不合題意，舍去）.

答：每個支干長出9個小分支.

【點評】本體是傳播類的問題，但與例1甲型H1N1流感病毒的傳播問題也有些許差別，流感傳播者第一天傳染后，第二天第三天還繼續參與傳播；而支干傳播問題，主干傳播給支干后，主干就不參與繼續傳播，只由支干來傳播給小分支.

練練身手2：

解：設垂直于墻的一邊為x米，由題意得：x（58-2x）=200，解得：x1=25，x2=4.

經檢驗x1=25，x2=4都符合題意.

∴另一邊長為8米或50米.

答：當矩形的長為25米時寬為8米，當矩形的長為50米時寬為4米.

（作者單位：江蘇省南京師范大學第二附屬初級中學）