具有脈沖擴散和擴散時滯的單種群模型研究*

黃玲智(重慶師范大學數(shù)學學院，重慶401331)

具有脈沖擴散和擴散時滯的單種群模型研究*

黃玲智
(重慶師范大學數(shù)學學院，重慶401331)

研究了兩斑塊間具有脈沖擴散和擴散時滯的對數(shù)增長單種群模型，利用脈沖微分方程比較原理和離散動力系統(tǒng)頻閃映射理論，得到了系統(tǒng)持久性和周期解的全局穩(wěn)定性的充分條件.

脈沖擴散;擴散時滯;持久性;全局穩(wěn)定性

0　引言

近年來，很多學者對種群的擴散現(xiàn)象進行了深入的研究［1-3］.擴散是自然界很普遍而且有規(guī)律的現(xiàn)象，比如，鳥兒在冬季來臨時會進行遷徙，但是它們并不在其他季節(jié)擴散.種群在擴散過程中會出現(xiàn)一些損失而且擴散需要時間.

考慮具有脈沖擴散和擴散時滯的對數(shù)增長單種群模型:

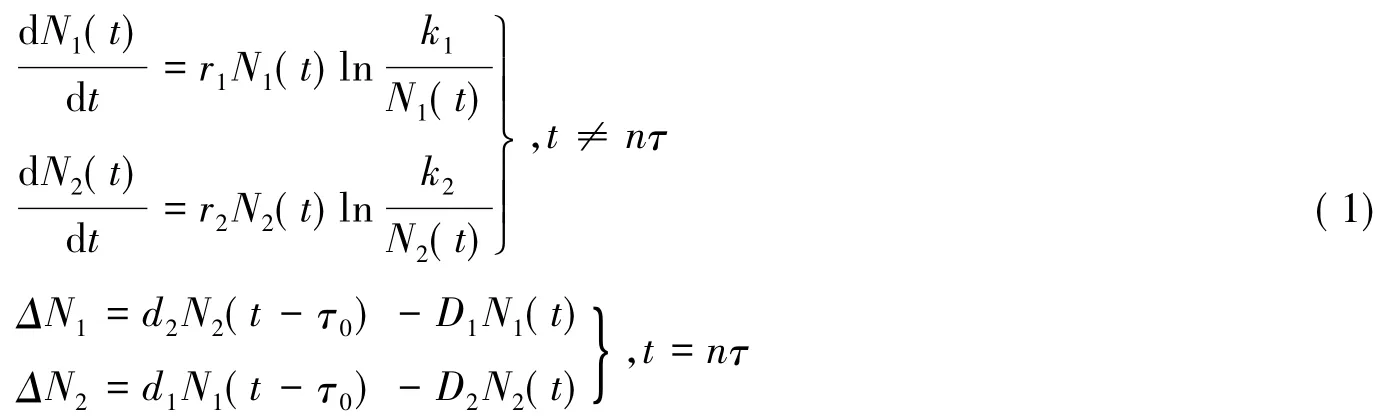
其中Ni(t)(i=1，2)表示t時刻第i個斑塊的種群密度，ri(i=1，2)表示第i個斑塊的內稟增長率，Di(i=1，2)表示種群Ni從第i個斑塊的移出率，di表示種群Ni遷移到第i個斑塊的遷入率，在這里假設0≤di＜Di＜1，也就說明在斑塊間的擴散過程中，種群存在損失，τ0表示種群在擴散過程中所用的時間.

1　預備知識

考慮如下非線性脈沖系統(tǒng):

其中r，k表示正數(shù)，0＜p＜1.

引理1［4］系統(tǒng)(2)存在唯一全局漸進穩(wěn)定的正周期解.

引理2［5］令是連續(xù)映射并在內具有一階導數(shù)，假設DF(0)存在并且另外假設:

(A)當x＞0時，DF(x)＞0.

(B)當0＜x＜y時，DF(y)＜DF(x).

如果F(0)=0，令λ=ρ(DF(0)).如果λ≤1，那么對一切x≥0，F(xiàn)n(x)→0，n→∞;如果λ＞1，那么，或者對一切x＞0，F(xiàn)n(x)→∞，n→∞;或者F存在唯一非零不動q.對于后一種情況q＞0并且對一切x＞0，有Fn(x)→q，n→∞.

如果F(0)≠0，對一切x≥0，或者Fn(x)→∞，n→∞;或者F存在唯一不動q.對于后一種情況q＞0，并且對一切x＞0，有Fn(x)→q，n→∞.

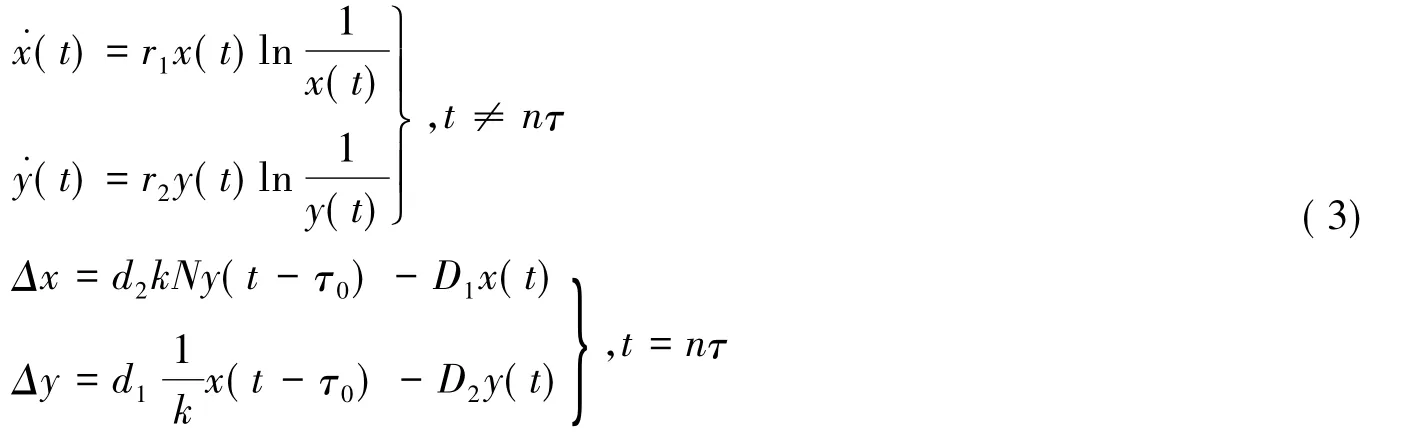
對系統(tǒng)(3)的前兩個方程，在相鄰脈沖點之間進行積分得

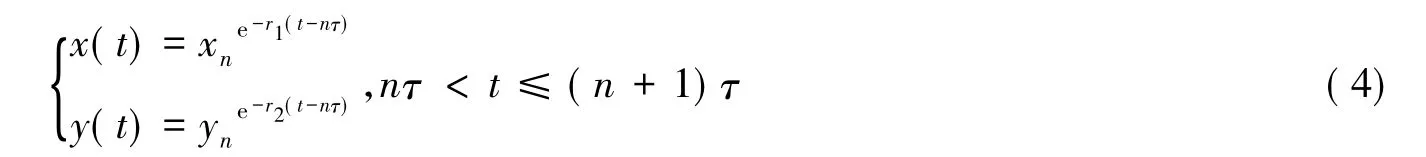
考慮系統(tǒng)(3)的后兩個方程，得到如下的頻閃映射:

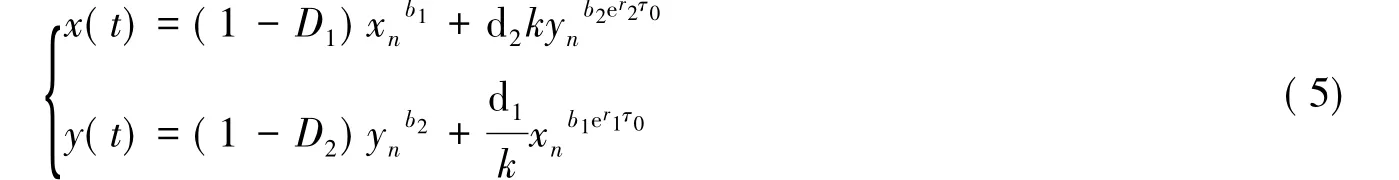
2　持久性

定理1系統(tǒng)(1)是持久性的.

證明首先證明系統(tǒng)(1)一致有上界.令(N1(t)，N2(t))是系統(tǒng)(1)的任意解，初值N(0)＞0，V(t)= N1(t)+N2(t)，λ0=min{r1，r2}，當t≠nτ時，有

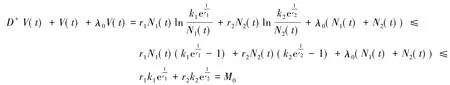
最后證明系統(tǒng)(1)的所有解一致有下界.當di≥0(i=1，2)，有

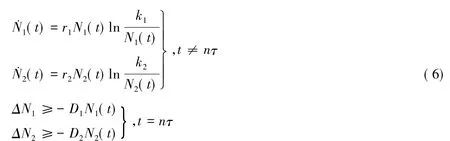
在這個系統(tǒng)(6)中N1(t)，N2(t)沒有任何聯(lián)系，可以將它們獨立出來.

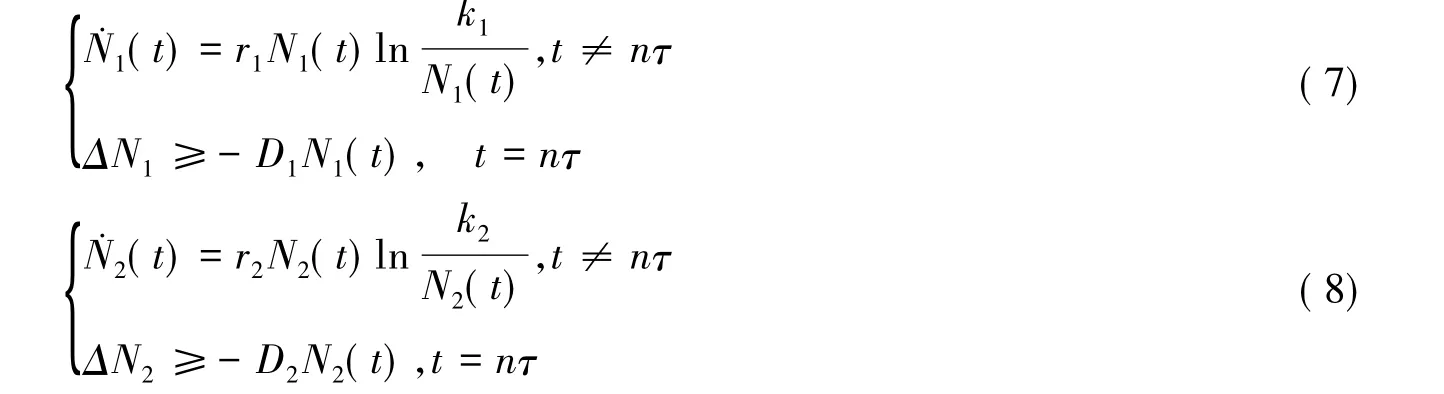
考慮系統(tǒng)(7)的脈沖比較系統(tǒng):

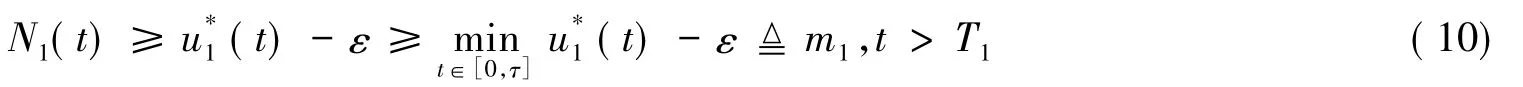
同理可得，對于充分小的ε＞0，存在一個T2＞0，有

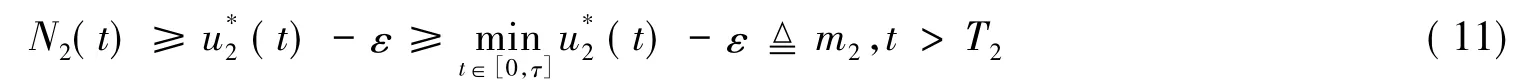
定理1的證明結束.

3　正周期解的穩(wěn)定性

首先證明系統(tǒng)(5)存在唯一的正不動點，即系統(tǒng)(1)存在唯一的正周期解.

定理2當(H1):D1≥d2k和(H2):b1+b2+d1d2＜1成立時，系統(tǒng)(5)存在唯一的正不動點.

證明由系統(tǒng)(5)，得到以下系統(tǒng):

由系統(tǒng)(12)得到

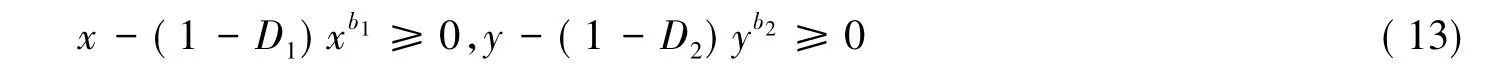
由系統(tǒng)(12)可得

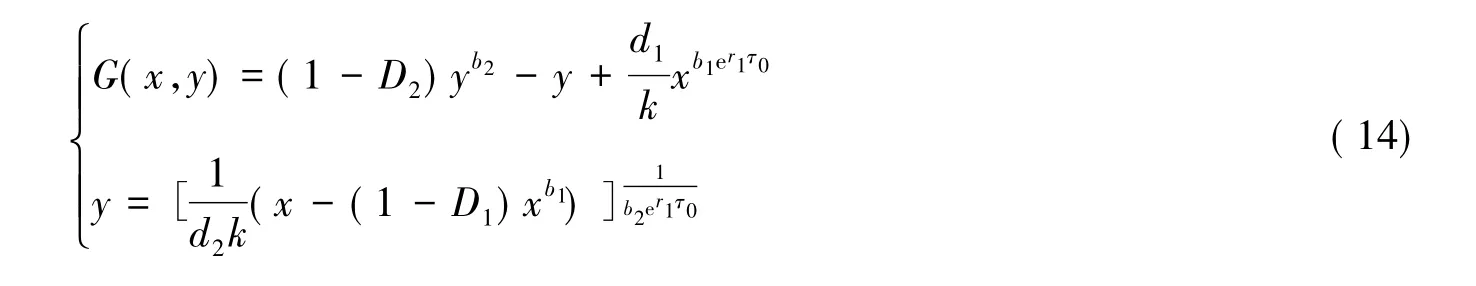
存在(x*，y*)滿足，使得

通過式(14)可得

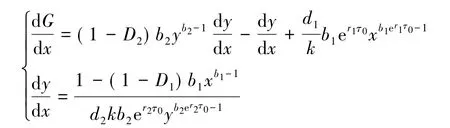
故

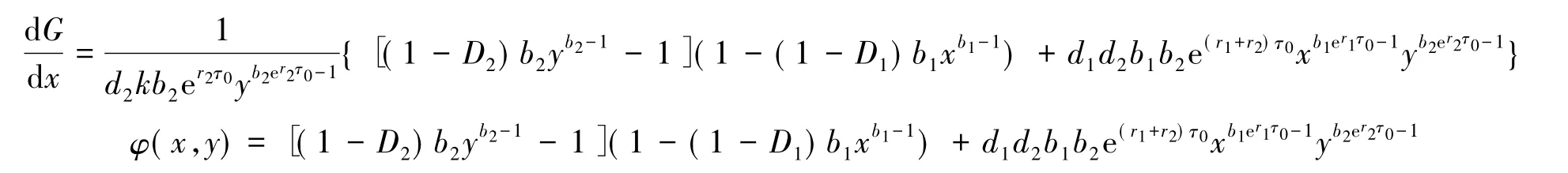
則

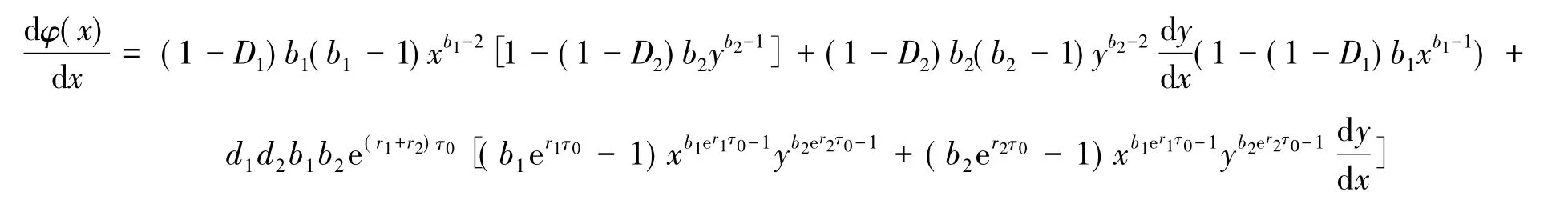
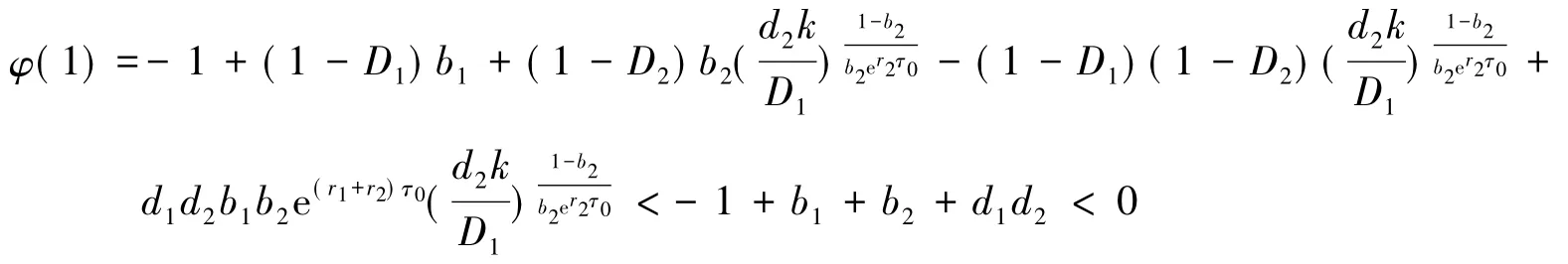
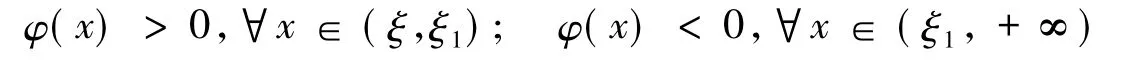
于是有

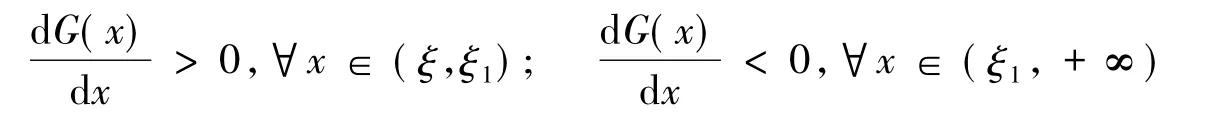
接下來，將證明系統(tǒng)(5)的正不動點(x*，y*)是全局穩(wěn)定的，也就是系統(tǒng)(1)的正周期解是全局漸進穩(wěn)定的.

定理3如果(H1)和(H2)成立，對于每一個(x，y)＞(0，0)，都有

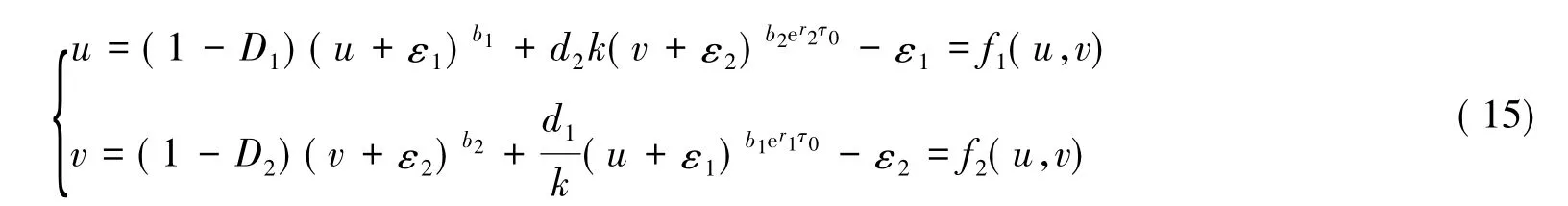
因為

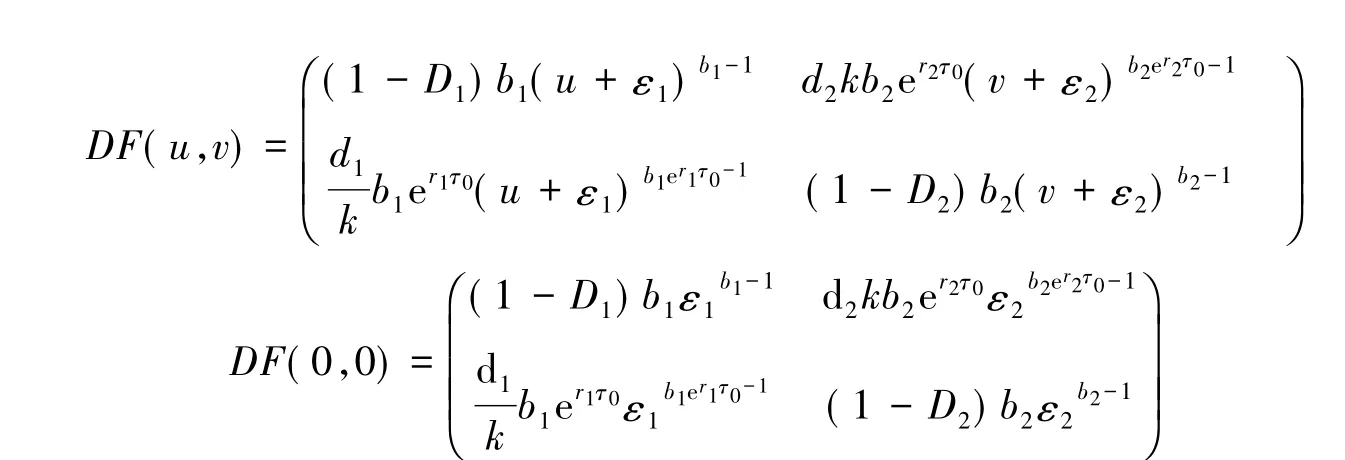
［1］WANG LM，LIU Z J，JH.Impulsive Diffusion In Single Species Model［J］.Chaos，Solitons and Fractals，2007(33):1213-1219

［2］WAN H Y，ZHANG L，LIH L.A Single Species Modelwith Symmetric Bidirectional Impulsive Diffusion and Dispersal Delay［J］.Applied Mathematics，2012(3):1079-1088

［3］JIAO J J，YANG X S，CAI SH.Dynamical Analysis of a Delayed Predator-prey Model with Impulsive Diffusion Between Two Patches［J］.Mathematics and computers in simulation，2009(80):522-532

［4］JIA JW，LI C H.A Predator-prey Gompertz Model with Time Delay and Impulsive Perturbations On the Prey［J］.Discrete Dynamical in Nature and Society，2009(2009):15-19

［5］AMITH H L.Cooperative System of Differential Equations with Concave Nonlinearities［J］.Nonlinear Anal TMA，1986(10): 1037-1052

Research on a Single Species Model with Impulsive Diffusion and Dispersal Delay

HUANG Ling-zhi
(School of Mathematical Sciences，Chongqing Normal University，Chongqing 401331，China)

This paper researches a single species model in logarithmic growth with impulsive diffusion and dispersal delay.Using the comparison theorem of impulsive differential equation and the discrete dynamical system，the permanent sufficient conditions of the system is obtained，and the system has a global stability positive periodic solution.

impulsive diffusion;dispersal delay;permanent;global stability

O175

A

1672－058X(2015)09－0005－05

10.16055/j.issn.1672－058X.2015.0009.002

2015－03－15;

2015－04－28.

國家自然科學基金(11471061);重慶市自然科學基金(CSTC2014jcyjA40004).

黃玲智(1991-)，女，湖南懷化人，碩士研究生，從事微分方程及其應用研究.