融數學建模思想于數學分析教學的探討*

張四保，宋愛麗(喀什師范學院數學系，新疆喀什844008)

融數學建模思想于數學分析教學的探討*

張四保，宋愛麗
(喀什師范學院數學系，新疆喀什844008)

“數學分析”是數學類各專業的一門主干基礎課程，該課程的教學存在著一定的難度;將數學建模思想與方法融入“數學分析”課程的教學是提高該課程教育教學質量與培養學生創新實踐能力的一條有效途徑，就融數學建模思想方法于數學分析教學過程中，提出幾點想法.

數學分析;數學建模;思想;教學

“數學分析”課程是數學類數學與應用數學、信息與計算科學、統計學等專業的一門主干基礎課程.學好“數學分析”課程是學好其他一些后繼課程如“微分方程”、“復變函數”、“實變函數”、“泛函分析”與“概率論與數理統計”等課程的必備基礎.同時“數學分析”課程也是以更高層次、更深入地理解中學數學教材所必需的基礎.通過“數學分析”課程基本知識的傳授與相關習題、實例的訓練，使學生養成嚴謹務實的學風，邏輯思維能力，分析和解決問題的能力有進一步提高.特別是注重學生發現問題、分析問題、解決問題的數學思想的培養.力爭為把學生培養成既有嚴謹的邏輯思維能力、又有科學創新精神的人才打下良好的基礎.因此該課程的教學好壞在一定程度上關系到學生數學思維與數學素質的培養與提高.

1　數學建模及其思想內涵

模型是為了一定目的，對客觀事物的一部分進行簡縮、抽象、提煉出來的原型的替代物，集中反映了原型中人們需要的那一部分特征.

數學模型(Mathematical Model)是關于部分現實世界和為一種特殊目的而做的一個抽象的、簡化的結構.具體來說，數學模型就是為了某種目的，用字母、數字及其他數學符號建立起來的等式或不等式以及圖表、圖像、框圖等描述客觀事物的特征及其內在聯系的數學結構表達式.

數學建模(Mathematical Modeling)簡單理解就是建立數學模型的全過程，也就是在深入調查研究，了解實際問題，做出合理的簡化假設，分析其內在規律等工作的基礎上，獲得數學模型，然后通過求解、計算得到的模型結果來解釋實際問題，并接受實際的檢驗.數學建模的一般步驟如圖1所示，全過程如圖2所示.

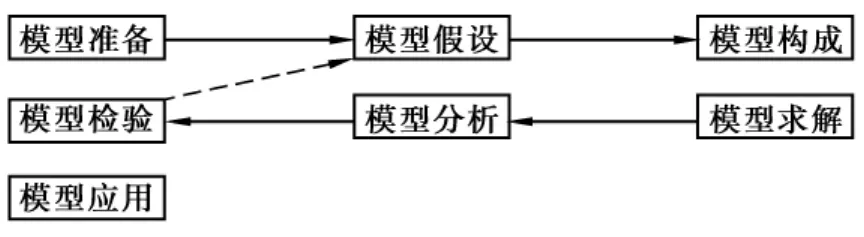
圖1　數學建模的一般步驟

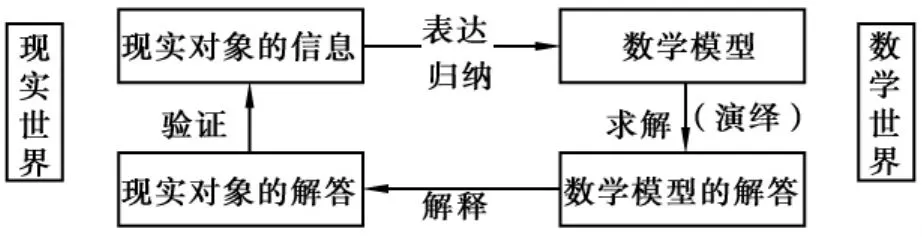
圖2　數學建模的全過程

2　融數學建模思想于“數學分析”課程中的作用與意義

作為數學類最重要的基礎課之一，數學科學的邏輯性和歷史繼承性決定了“數學分析”在數學科學中舉足輕重的地位，數學的許多新思想，新應用都源于這一堅實的基礎.“數學分析”由于對微積分在理論體系上的嚴格化和精確化，確立了在數學科學中的基礎地位，并運用于自然科學的各個領域.同時，數學研究的主體是經過抽象后的對象，數學的思考方式有鮮明的特色，包括抽象化、邏輯推理、最優分析、符號運算等，這些知識和能力的培養需要通過系統、扎實而嚴格的基礎教育來實現，“數學分析”課程正是其中最重要的一個環節.

“數學分析”的教學存在著諸多問題.例如，對于剛進入大學的新生，不太適應大學教師的教學方法與模式;學生認為“數學分析”課程過于抽象，與實際生活距離較遠，對該課程缺乏學習熱情和動力［1］.融數學建模思想方法于“數學分析”課程的教學中，配合適量的數學模型內容進行教學，有利于學生對基礎理論知識的掌握，提高學生分析問題、解決問題的數學實踐應用能力，同時可以激發學生學習數學的積極性與熱情，提高自身素質和素養.可以起到以下作用:激發學生的參與探索的興趣;增強聯系數學理論與實際運用的能力;促進“數學分析”教學的改革;提高大學生的數學素質.

3　融數學建模思想于“數學分析”教學

“數學分析”教學中要求掌握的很多內容可以看作是數學建模的模型求解階段，比如函數的可微性、定積分、重積分、曲線積分、曲面積分的計算等［2］.因此，在實際教學過程中，應適當結合數學模型的建模全過程來進行講解，使學生了解問題的來龍去脈，逐步的進行分析、求解等，使學生在學習的過程中系統地了解與掌握分析問題、解決問題的思想與方法，以提高學生學習數學的興趣，更好的培養學生應用數學的能力.

3.1融數學建模思想于概念、定義教學之中

從恰當的案例中引入概念是將數學建模思想融入“數學分析”課程教學的重要形式［3］.“數學分析”課程中有很多非常重要的概念，如函數、極限、連續、導數、微分、定積分、重積分、級數等，這些概念都是從一些具體問題出發，抓住其在數量關系等方面的共同本質和特性而加以概括、抽象出來的.在一些重要概念教學過程中，對概念的引入，任課教師要精心設計，這樣在知識傳授過程中，讓學生學會數學思想、方法，領會數學的精神實質，知曉知識點的來龍去脈，使學生明白那些看似枯燥無味的概念不是頭腦中所固有的，而是有著很強的現實背景，有其特有的物理原型和表象的.

例如，對于定積分概念，初學時學生倍感這一概念很抽象.其實，這一概念是在很多具體原型的基礎之上抽象而得到的，如求曲邊梯形的面積、旋轉體的體積等.在教學過程之中可以將求曲邊梯形面積作為原型，借助“不變代變”的思想，通過“分劃→近似→求和→取極限”4個步驟，最終將無限細分所得的近似值的極限定義為曲邊梯形面積的值，從而這個幾何問題得到解決［4］.通過這一數學模型來進行教學，可以使學生更好地學習并理解這一概念，比把概念用抽象、不易理解的數學符號直接呈現給學生要生動、形象、有趣的多，更容易使學生記住、理解、掌握知識點，學習數學的熱情勢必會更高，可以達到事半功倍的教學效果.

又例如，在講授無窮級數這一概念時，為了引入該概念，任課教師可以介紹“阿基里斯追龜悖論”.對于該悖論，教師在分析完該悖論的內容、產生的原因、哲學辨析之后，可建立簡單的模型來解釋，其詳細過程可參見文獻［5］.芝諾悖論涉及到了無窮項求和，這是學生先前并未接觸到的，只是熟知有限項求和的相關內容.教師引導學生利用已學的有限項求和概念，結合已學的極限理論，逐漸給出無窮項求和的可能性及基本方法，極大地激發學生學習的興趣.

3.2融數學建模思想于定理、結論教學之中

“數學分析”中有很多較為抽象、不易理解的定理，如何講授這樣的定理，使學生更容易理解、掌握與靈活運用定理解決一些實際問題，這是教學過程的一大難點［6］.對于定理的證明，可將定理的結論視為是一個數學模型，將定理的條件視為模型的假設條件，即可根據預先設置好的問題情景逐步地引導學生發現定理的結論，最終建立相應的模型.這樣融入數學建模思想于教學的方法，一方面使學生學到了數學知識，另一方面讓他們體驗到探索、發現和創造的過程，是培養學生意識與創新能力的好途徑.

多年來，在講授數學課程的過程中，常常會遇到學生提出這樣一個問題:數學知識究竟有什么用?許多學生知道數學知識有用，必須學好，但在實際生活中似乎又看不到數學有什么用，也不知道怎樣用，在什么時候用，尤其是數學中的定理結論之類.這樣一來，學生會喪失學習的興趣.為了提高學生的興趣，培養學生的數學應用能力，在一些定理、結論的教學過程中，適時增加一些數學模型的實例.

案例:椅子能在不平的地面上放穩嗎［7］?

模型的假設:①4條腿一樣長，椅腳與地面點接觸，4只腳連線呈正方形;②地面高度連續變化，可視為數學上的連續曲面;③地面相對平坦，使椅子在任意位置至少3只腳同時著地.

模型的構成:利用正方形的對稱性，以椅腳連線為對稱，椅腳按O點進行旋轉，其旋轉示意圖如圖3所示，用θ(對角線與x軸的夾角)表示椅子位置，4只腳著地表明4個椅腳與地面的距離為零，其中這4個距離都是θ的函數.根據正方形對稱性，4個距離中可以進行組合，實際考慮兩個距離:A，C兩腳與地面距離之和，用f(θ)表示;B，D兩腳與地面距離之和，用g(θ)表示.根據假設②可知，f(θ)與g(θ)為連續函數，椅子在任意位置至少3只腳著地，于是正方形ABCD繞O點旋轉，對任意θ，f(θ)，g(θ)中至少一個為0.這樣，椅子能不能在不平的地面上放穩這一問題轉化為數學模型:已知f(θ)與g(θ)為連續函數，對任意θ，f(θ)·g(θ)= 0，且g(θ)=0，f(θ)＞0，證明存在θ0，使f(θ0)=g(θ0)=0.

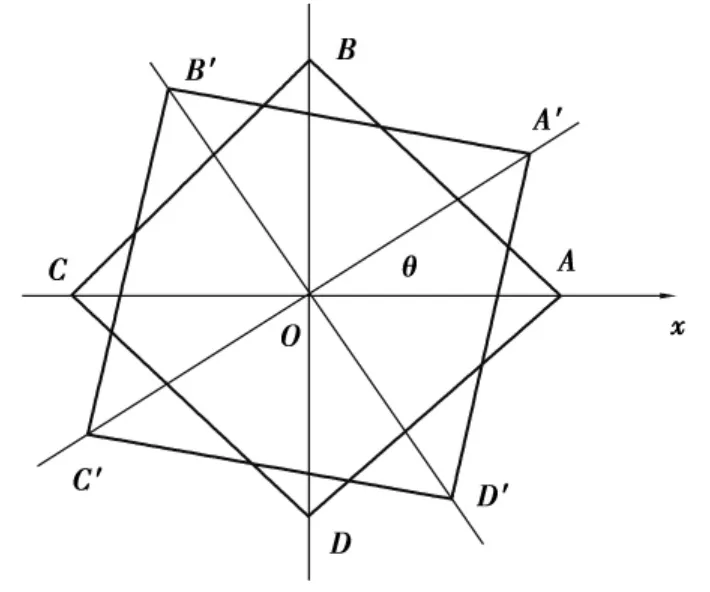
圖3　椅腳旋轉示意圖

模型求解:由連續函數的根的存在定理解決此問題.

這樣把理論應用到實踐中去，解決一些實際問題，可以達到加深理解，深化、鞏固所學理論的作用.

3.3融數學建模思想于作業之中

作業是學生經過獨立思考，自覺、有目的地分析問題、解決問題，將學得的知識運用于實際的智力活動過程，是鞏固新授知識，形成技能技巧，培養良好的思維品質，發展學生智力的重要途徑，是課堂教學過程中不可跨越的一環.通過寫作業可以檢查學生學習的結果，加深對知識的理解和記憶，充分發揮學生的智慧和潛力，同時也有助于培養學生的思維能力.針對“數學分析”理論性較強的特點，有目的讓學生解決一些實際問題.只有把理論應用到實踐中去，解決幾個實際問題，才能達到理解、深化、鞏固所學理論的效果［8］.在“數學分析”的習題課教學中，教師可根據實際情況適時將教材中的一些純數學問題進行改編、加工成一些具有實際意義的應用題，引導學生運用所學的數學分析有關理論知識以及思想、方法來解決問題.這一過程事實上就是進行數學建模的過程.通過這樣應用題目的解決，使學生能夠更加深刻地體會到學習“數學分析”的樂趣和意義.

4　融數學建模思想于“數學分析”教學中應注意的問題

融數學建模思想于“數學分析”教學中，一定要把握度的問題，在一些問題上不要刻意去追求.由于課時有限，課堂教學過程中“插入”內容課時不宜安排過多，否則將會影響課程教學計劃;但又不能“蜻蜓點水”，沒有一定的深度.這就要求教師要充分研究“數學分析”教學內容，精選合適的案例，充分發揮數學建模的思想，并將之作為“數學分析”課程教學的延伸性和推廣性內容來講授.在這過程中，需注意以下幾條:注意循序漸進性，切記急功近利;案例要精，反映主題;正確處理好與數學分析課程學習的關系.

5　結語

目前，在全國大學生數學建模大賽活動的影響與推動下，“數學建模”與“數學實驗”等課程已是各個高校高年級的選修或必修課程.“數學分析”是大一年級的基礎課程之一，融數學建模思想、方法于“數學分析”課程的教學中，這對教育教學改革具有積極的意義，這將有助于提高學生應用數學意識與能力，逐漸提高學生利用數學理論與原理解決實際問題的能力.在具體實施的過程中，教師應處理好教學內容的“嚴謹性”和“實用性”的關系，以促進教育教學改革的持續良性發展.

［1］師文英，陳俊敏，高紅亞.關于數學分析課程教學的幾點思考［J］.教育教學論壇，2011(27):141-142

［2］徐艷艷，陳廣貴.關于如何激發學生學習數學分析課興趣的幾點思考［J］.高等教育研究，2014，31(1):18-20

［3］李聲鋒，張裕生，梅紅.將數學建模思想融入“數學分析”課程教學的探索與實踐［J］.赤峰學院學報，2011，27(7):247-248

［4］王娟，侯玉雙，劉興薇，等.數學建模思想在數學分析課程教學中的應用［J］.科技信息，2013(23):42-44

［5］羅朝暉.關于數學建模思想滲入數學分析教學的思考［J］.教育與職業，2007(20):114-115

［6］黃敬頻.數學建模思想在數學分析課程教學中的應用［J］.廣西大學學報，2003，28(s):21-24

［7］姜啟源，謝金星，葉俊.數學模型［M］.4版.北京:高等教育出版社，2011

［8］韋程東，羅雪晴，程艷琴.在數學分析教學中融入數學建模思想的探索與實踐［J］.高教論壇，2008(3):77-79

Discussion on Infiltrating the Idea of Mathematical Modeling in Mathematical Analysis Teaching

ZHANG Si-bao，SONG Ai-li
Department of Mathematics，Kashgar University，Kashgar 844008，China

Mathematical Analysis is an essential course for themajor ofmathematical science.There are some difficulties in teaching this course.To infiltrate the idea and method ofmathematicalmodeling in the Mathematical Analysis teaching can improve the quality of education and teaching，and it is one of the effectivemethod of training students’innovative and practical ability.This paper proposes some thoughts on the infiltration.

Mathematical Analysis;mathematicalmodeling;idea;teaching

G642;O141

A

1672－058X(2015)09－0098－04

10.16055/j.issn.1672－058X.2015.0009.023

2014－07－17;

2015－01－15.

喀什師范學院教研教改重點課題階段性成果(KJGZ1301).

張四保(1978-)，男，江西峽江人，講師，碩士，從事數論研究.