非奇異M矩陣Hadamard積的特征值界的新序列*

蔣建新，李艷艷(文山學(xué)院數(shù)理系，云南文山663000)

非奇異M矩陣Hadamard積的特征值界的新序列*

蔣建新，李艷艷
(文山學(xué)院數(shù)理系，云南文山663000)

利用非奇異M矩陣A的逆矩陣A－1元素單調(diào)的上下界序列和改進(jìn)的圓盤定理，得到了M矩陣B與A－1的Hadamard積以及最小特征值下界單調(diào)遞減的新估計(jì)式.

M矩陣;Hadamard積;最小特征值;下界

關(guān)于非奇異M矩陣A的逆矩陣A－1與M矩陣B的Hadamard積的最小特征值下界的研究，已得到許多估計(jì)式［1－6］.但這些估計(jì)式有些涉及矩陣的特征值，有些涉及A－1的元素，有些又涉及A的譜半徑，當(dāng)矩陣階數(shù)較大時(shí)計(jì)算比較困難.此處利用非奇異M矩陣A的逆矩陣A－1元素單調(diào)的上下界序列和改進(jìn)的圓盤定理，得到了下界單調(diào)遞減的一系列新估計(jì)式.這些估計(jì)式只與矩陣的元素有關(guān)，當(dāng)?shù)螖?shù)較高時(shí)，幾乎可以逼近真值.

1　預(yù)備知識(shí)

首先引入一些記號(hào):

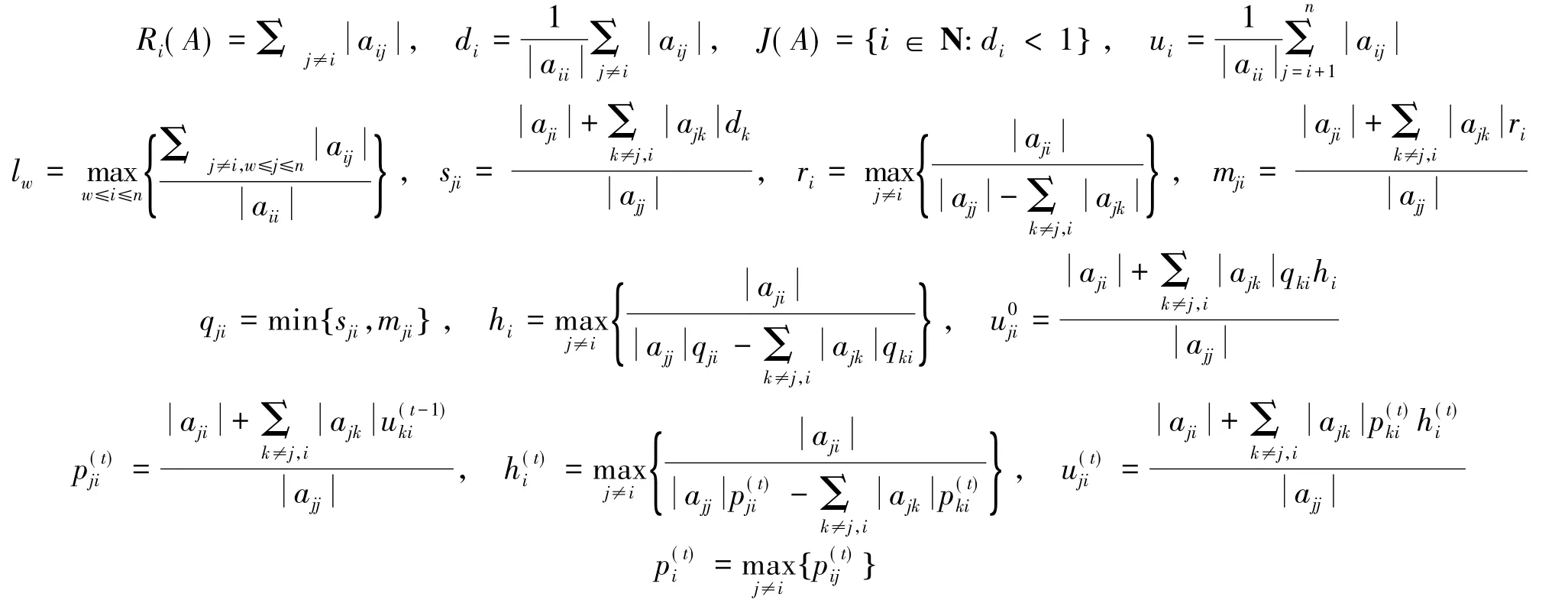
其次，給出一些定義和引理.

定義1［1］設(shè)，如果則稱A為Z矩陣.

定義2［1］設(shè)為Z矩陣，若A可表示為，其中，則稱A為M矩陣，當(dāng)α＞ρ(P)時(shí)，稱A為非奇異M矩陣，非奇異M矩陣的集合用Mn表示.

定義3［1］σ(A)={λ1，λ2，…，λn}表示矩陣A=(aij)∈Cn×n的n個(gè)特征值λ1，λ2，…，λn組成的集合，稱為A的譜，A的最小特征值記作τ(A)=min{Re(λ):λ∈σ(A)}.

定義4［1］設(shè)稱為A和B的Hadamard積.

引理1［1］若A=(aij)∈Rn×n是M矩陣，則存在正對角矩陣D，使D－1AD是嚴(yán)格對角占優(yōu)矩陣，也是M矩陣.

引理2［1］設(shè)A，B，C，D∈Rn×n，其中C，D是對角矩陣，則

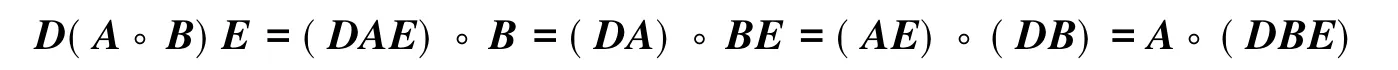
引理3［2］設(shè)A=(aij)∈Cn×n，x1，x2，…，xn是一組正實(shí)數(shù)，則A的所有特征值包含在復(fù)平面C的如下區(qū)域中:

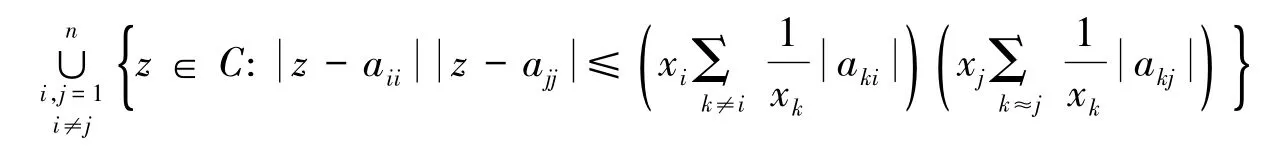
引理4［3］設(shè)A=(aij)∈Rn×n是行嚴(yán)格對角占優(yōu)的M矩陣，則i，j∈N，j≠i，t=1，2，…，有式(1)(2)成立:

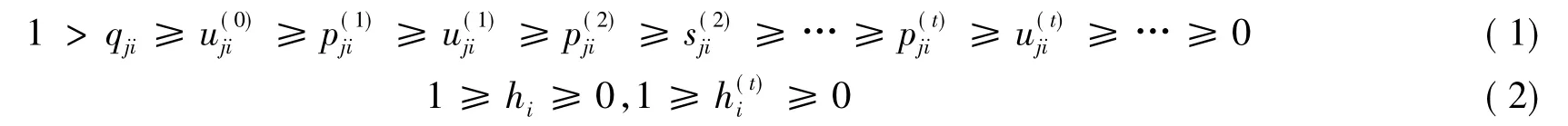
引理5［3］設(shè)A=(aij)∈Rn×n是行嚴(yán)格對角占優(yōu)M矩陣，則A－1=(βij)存在且有下列不等式(3)成立:

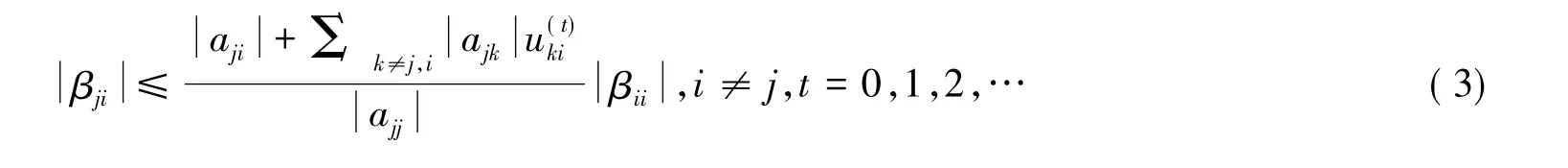
2　主要結(jié)果

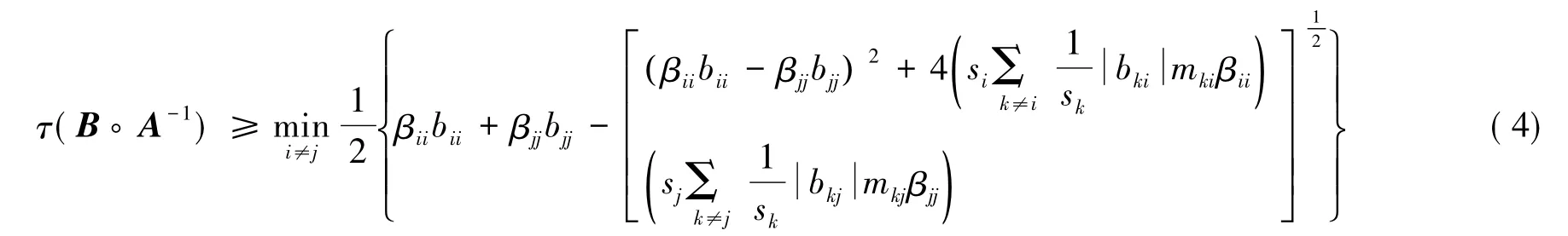
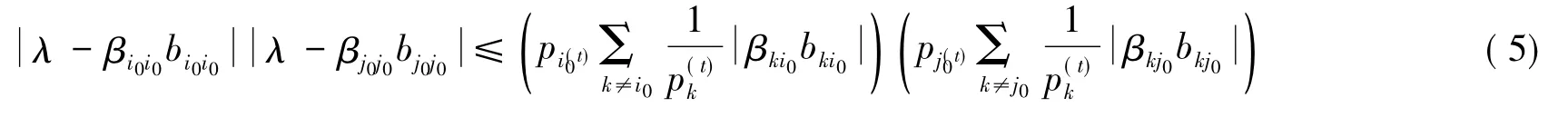
又因?yàn)?/p>

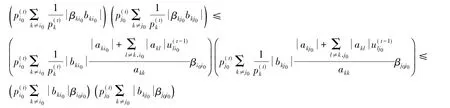
則有

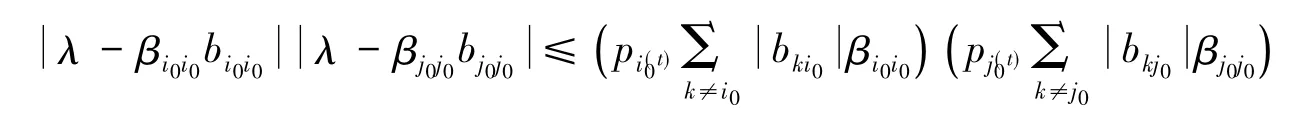
化簡整理得

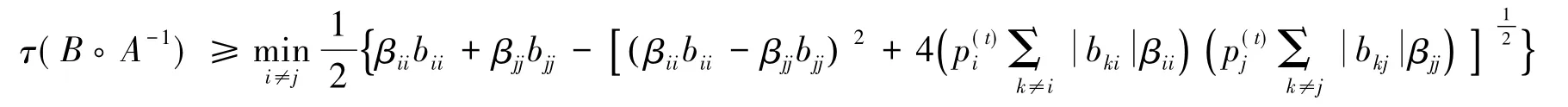
2)若A，B有一個(gè)可約，類似文獻(xiàn)［5］中定理2.2.2的證明知此時(shí)定理1也成立.

3　數(shù)值例子

假設(shè)

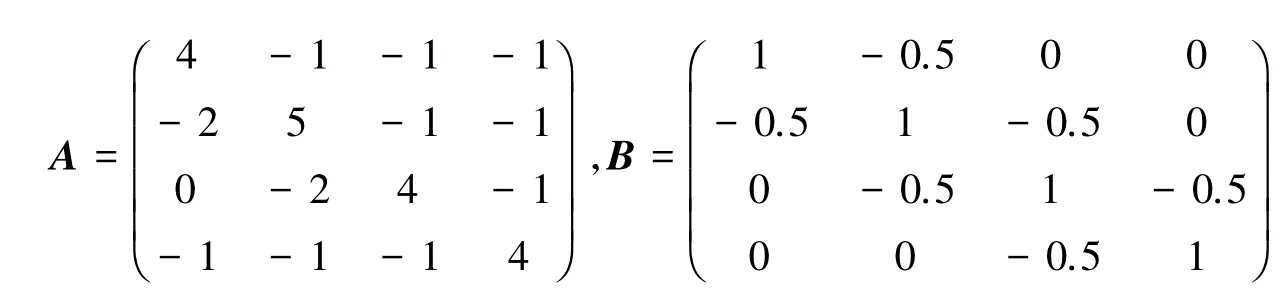
此例進(jìn)一步說明了所得結(jié)果的有效性.

［1］陳景良，陳向暉.特殊矩陣［M］.北京:清華大學(xué)出版社，2000

［2］王德鳳.矩陣Hadamard積與Fan積的最小特征值與譜半徑界的估計(jì)［D］.昆明:云南大學(xué)，2011

［3］趙建興.M-矩陣最小特征值估計(jì)及其相關(guān)問題研究［D］.昆明:云南大學(xué)，2014

The New Sequence of the Eigenvalue Bounds of the Hadamard Product of Nonsingular Matrix

JIANG Jian-xin，LIYan-yan
(Department of Mathematics and Physics，Wenshan University，Wenshan 663000，China)

By using the upper and lower bounds on themonotone sequence for inversematrix A－1elements of nonsingular M matrix A and improved disk theorem ofmatrix，this paper obtains the new estimator of theminimum eigenvalue bounds decreasingmonotonically of Hadamard product of M matrix B and A－1.

matrix;Hadamard product;minimum eigenvalue;lower bound

O151.2

A

1672－058X(2015)09－0020－03

10.16055/j.issn.1672－058X.2015.0009.005

2015－03－13;

2015－04－02.

云南省教育廳科學(xué)研究基金項(xiàng)目(2013Y585);文山學(xué)院重點(diǎn)學(xué)科數(shù)學(xué)建設(shè)項(xiàng)目(12WSXK01).

蔣建新(1981-)，男，講師，碩士，從事矩陣?yán)碚摷捌鋺?yīng)用研究.