初等變換在向量組的線性相關性中的應用*

張平平，徐陽棟(重慶郵電大學理學院，重慶400065)

初等變換在向量組的線性相關性中的應用*

張平平，徐陽棟
(重慶郵電大學理學院，重慶400065)

線性方程組的解及向量組的線性相關性是線性代數的核心內容，而初等變換是研究它們的最有力的工具，因此應用好這一工具對學習線性代數非常有幫助;用“提問—總結—舉例”的方式給學生闡述了初等變換在向量組的線性相關性中的應用.

初等變換;向量組;最大線性無關組;線性相關

為了便于敘述，給出下面已熟悉的初等變換的性質作為引理.

引理1［1］設A是一個m×n矩陣，對A施行一次初等行變換，相當于在A的左邊乘以相應的m階初等矩陣;對A施行一次初等列變換，相當于在A的右邊乘以相應的n階初等矩陣.

引理2［1］方陣A可逆的充分必要條件是存在有限個初等矩陣P1，P2，…，Pl，使得A=P1P2，…，Pl.

引理3［1］對于m×n矩陣A，可經過一系列的初等行變換化成行最簡形矩陣.

下面通過“提問題—解決問題—總結—舉例”的方式給出線性變換在向量組的線性相關性中的應用.

若矩陣P是一m階可逆矩陣，矩陣A=［α1，α2，…，αn］，B=［β1，β2，…，βn］均為m×n矩陣，αj，βj(j=1，2，…，n)分別是它們的列向量，且滿足PA=B.

問題1試證向量組βi1，βi2，…，βir是向量組β1，β2，…，βn的最大線性無關組的充分必要條件是向量組αi1，αi2，…，αir是向量組α1，α2，…，αn的最大線性無關組.

證明只證充分性，必要性可類似地證明.由題意得

i)首先要證向量組βi1，βi2，…，βir線性無關.令

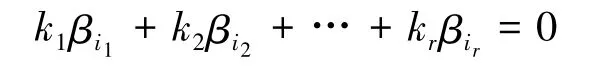
把式(1)代入得

由P是可逆矩陣，左右兩邊同時乘以P－1得，

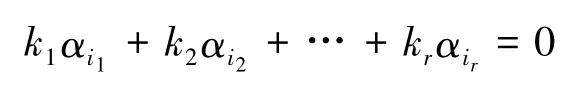
再由假設向量組αi1，αi2，…，αir是最大無關組，知αi1，αi2，…，αir線性無關，從而有

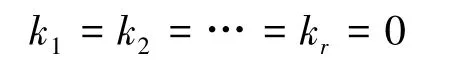
于是向量組βi1，βi2，…，βir線性無關.

ii)其次要證βi(i=1，2，…，n)可由向量組βi1，βi2，…，βir線性表出.

由向量組αi1，αi2，…，αir是向量組α1，α2，…，αn的最大線性無關組，知αi(i=1，2，…，n)可由向量組αi1，αi2，…，αir線性表出，即存在數ki1，ki2，…，kir使得

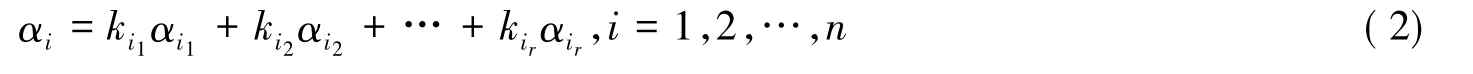
對式(2)左右兩邊同時乘以矩陣P，并結合式(1)，得

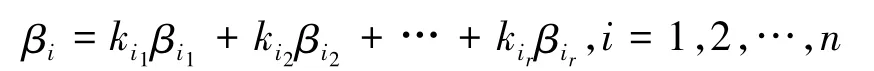
即證βi(i=1，2，…，n)可由向量組βi1，βi2，…，βir線性表出.

由i)，ii)知充分性得證.

由問題1知，若在向量組β1，β2，…，βn中很容易找到其最大無關組，則就可以得到向量組α1，α2，…，αn相應的一個最大線性無關組.知道行最簡形矩陣的非零行的第一個非零元素所在的列向量就是該矩陣的列向量所組成的向量組的一個最大無關組.同時由問題的證明過程知道，βi(i=1，2，…，n)由其最大線性無關組線性表示的表出系數與αi(i=1，2，…，n)由其相應的最大線性無關組線性表示的表出系數相同;而行最簡形矩陣的列向量很容易寫出由其非零行的第一個非零元素所在的列向量的線性表示的表出系數.再根據引理1，2及3就有找一給定向量組的最大線性無關組并把其余的向量用該最大線性無關組線性表示的方法，并以命題的方式總結如下:

命題1將矩陣A=［α1，α2，…，αn］進行一系列的初等行變換使其化成行最簡形矩陣B=［β1，β2，…，βn］，且設該最簡形矩陣中的非零行的第一個非零元素所在的列標依次為i1，i2，…，ir，且有則向量組αi1，αi2，…，αir就是向量組α1，α2，…，αn的一最大線性無關組，并且

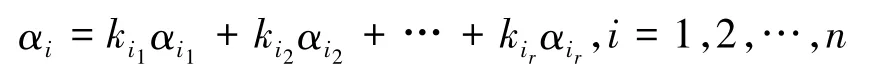
從問題中提煉出方法，然后再歸納總結，這是數學當中重要的研究手段［2］.

例1設矩陣

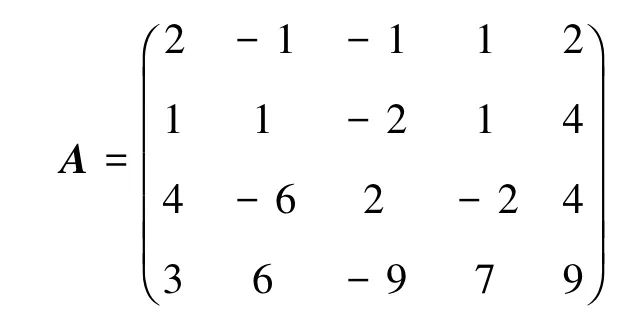
求矩陣A的列向量組的一個最大線性無關組，并把不屬于最大線性無關組的列向量用最大線性無關組線性表示.

解對矩陣A施行一系列的初等行變換變為行最簡形矩陣

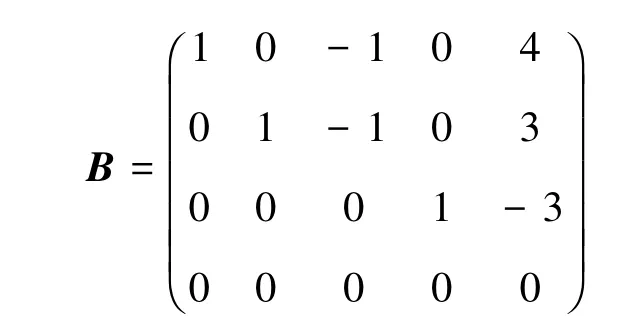
顯然B中的非零行的第一個非零元素所在的列的列標分別為1，2，4，由命題1知道

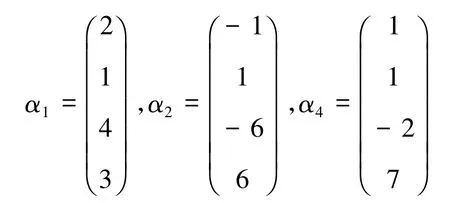
為該列向量組的最大線性無關組.在B的列向量組中，很容易得到如下線性表示式

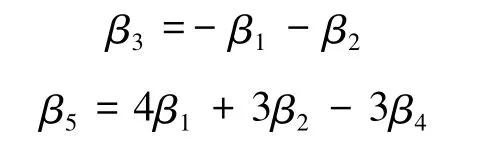
由命題知道

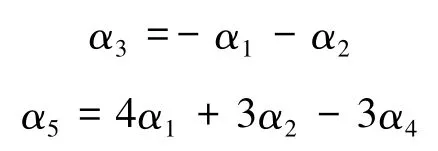
盡管隨著計算機的發展，判斷一向量組的線性相關性及線性表示問題很容易在計算機上實現［3］，然而這些是要在相應理論研究的基礎上實現的.因此向量組的線性相關性及線性表示問題的理論研究還是非常有意義的.

［1］同濟大學數學系.工程數學線性代數［M］.5版.北京:高等教育出版社，2007

［2］曾靜，程珍珍，耿立剛.定積分定義在證明和求極限中的應用［J］.重慶工商大學學報:自然科學版，2013，30(2):18-20

［3］孫祥凱，張付臣.例析線性規劃教學中解的判定準則［J］.科技文匯，2014(280):47-49

The Application of Elementary Transformation in the Linear Dependence of Vector Sets

ZHANG Ping-ping，XU Yang-dong
(School of Science，Chongqing University of Posts and Telecommunications，Chongqing 400065，China)

The solution to system of linear equations and the linear dependence of vector sets are the core content in linear algebra，and elementary transformation is a powerful tool to research them.Hence，it is very helpful tomaster the tool for learning linear algebra.This paper states the application of elementary transformation in the linear dependence of vector sets in the way of“asking question-summing up-taking example”.

elementary transformation;vector sets;maximal linearly independent subset;linearly dependence

O151.2

A

1672－058X(2015)09－0023－03

10.16055/j.issn.1672－058X.2015.0009.006

2015－01－17;

2015－03－10.

國家數學天元基金(11426055).

張平平(1985-)，女，江西上饒人，講師，博士研究生，從事數值線性代數研究.