一次還本付息債券利息調整探討

（廣州科技貿易職業學院 廣東廣州511442）

2007年賀飛躍同志的《一次還本付息債券應計利息會計核算的改進》（以下簡稱賀文）舉例說明到期一次還本付息債券的會計核算可能會出現“利息調整過度”現象。賀文所談的“利息調整過度”現象，是指到期一次還本付息、溢價發行的債券，在運用實際利率法對其溢價部分進行攤銷的過程中，出現記于“應付債券——利息調整”明細科目的累計攤銷額，超過原記于該明細科目的待攤銷溢價金額，從而導致后期需要在“應付債券——利息調整”賬戶中轉回所超金額的現象。隨后，王玉海同志在2008年發表了《一次還本付息債券應計利息會計核算的設計——兼與賀飛躍同志的商榷》（以下簡稱王文），指出賀文所舉例子的債券實際利率6.5537%，為使用插值法得出的估計實際利率，而非真實實際利率；并認為，賀文所謂的利息“調整過度”，是由于在應用實際利率法時，“使用插值法估算出的估計實際利率的結果”，因此，在使用實際利率法進行利息調整時，“只要找到真實的實際利率，就不會出現所謂的‘調整過度’現象”。對王文的這些觀點，筆者認為，也是值得商榷的。

一、賀文例子所用的債券實際利率，符合《企業會計準則》的相關定義，不能因為該利率可能是采用插值法估算出來的，就認為它不是真實的實際利率

《企業會計準則第22號——金融工具確認和計量》第十四條明確指出：實際利率，是指將金融資產或金融負債在預期存續期間或適用的更短期間內的未來現金流量，折現為該金融資產或金融負債當前賬面價值所使用的利率。我們再來看賀文所舉的例子：2007年1月1日某企業發行債券，面值500萬元，期限4年，年利率8%，按單利法計算，到期一次還本付息。該企業溢價發行債券，實際收到發行價款512萬元。按實際利率法計算：2007年1月1日債券賬面價值為512萬元，4年后債券賬面價值=500×（1+8%×4）=660 （萬元）。 設債券實際利率為 R， 則 512×（1+R）4=660，解得R=6.5537%。從以上解的過程來看，該債券實際利率6.5537%符合《企業會計準則》的相關定義。而且，筆者應用EXCEL軟件對該利率進行復核，證實這個數據是比較精確的（已精確到小數點后4位數）。

二、按實際利率計算到期一次還本付息債券的攤余成本及各期利息費用時，如果出現賀文中的“利息調整過度”現象，那只能歸因于債券面值、票面利率、債券期限和實際收到的發行價款等因素，而非王文所說的由于“使用插值法得出的估計實際利率而非真實實際利率”的結果

到期一次還本付息、溢價發行的債券，在其會計核算中出現利息調整過度現象的充分必要條件如下：1/R-1/i＜n-1（R＞0，i＞0，n≥2）；或者 A＜B＜[A（1+i·n-i）n/（1+i·n）n-1]（A（1+i·n）＞B＞A＞0，i＞0，n≥2）。 其中，A 為債券面值，B 為實際收到的發行價款，i為票面利率，n為債券期限，R為實際利率 （根據資金時間價值的相關公式，有 B（1+R）n=A（1+i·n），即 R 由債券面值、票面利率、債券期限和實際收到發行價款這些因素共同決定）。詳細的數學證明如下：

首先證明其必要性，分兩個步驟完成該項證明。第一步，證明對于到期一次還本付息、溢價發行的債券，第一期（假設債券于1月1日發行，第一期則指發行當年1月1日至12月31日的期間）計算的實際利息費用（攤余成本×實際利率），小于應計利息（債券面值×票面利率），即證明由，有，進而。 由于是溢價發行的債券，有 B＞A＞0，故因此，B·R·n＜A·i·n，兩邊除以 n，得 B·R＜A·i。這就證明了一次還本付息、溢價發行的債券，一開始對其溢價部分進行攤銷時，總是借記“應付債券——利息調整”科目，與發行時記于“應付債券——利息調整”貸方的溢價部分方向相反。第二步，再證明如果到期一次還本付息、溢價發行的債券在其會計核算中出現“利息調整過度”現象，那么，公式1/R-1/i＜n-1（R＞0，i＞0，n≥2）一定成立。 根據第一步驟的證明，前期溢價攤銷額記于“應付債券——利息調整”科目的借方，因此，如果存在“利息調整過度”現象，就會導致后期出現溢價攤銷額記于“應付債券——利息調整”科目貸方的情形。換句話說，如果出現“利息調整過度”，至少在最后一期會出現實際利息費用大于應計利息的情形 （這是因為攤余成本在逐期增大的緣故）。第n期（債券的最后一期）期初的攤余成本為 B（1+R）n-1，所以該期的實際利息費用為 B·R（1+R）n-1=B·R（1+R）n/（1+R），把 B（1+R）n=A（1+i·n）代入，有 B·R（1+R）n-1=A·R（1+i·n）/（1+R），而應計利息仍然是 A·i。 如果最后一期出現實際利息費用大于應計利息，則有B·R（1+R）n-1=A·R（1+i·n）/（1+R）＞A·i，整理后得 1/R-1/i＜n-1。 又由 1/R-1/i＜n-1，得 R＞i/（1+i·n-i），結合 B（1+R）n=A（1+i·n）及 B＞A，進一步得 A＜B＜A（1+i·n-i）n/（1+i·n）n-1（為簡潔起見，下文采用符號 F（i，n）表示（1+i·n-i）n/（1+i·n）n-1）。 必要性得證。

充分性的證明為以上必要性證明的逆過程，此處不再詳列。

在上述證明當中，我們不禁會問：對于到期一次還本付息、溢價發行的債券，總是可以找到滿足條件1/R-1/i＜n-1（R＞0，i＞0，n≥2）的 R 值嗎？ 它不會僅僅出現在某些特例中吧？這個問題交由以下的證明來回答。由上證明得知，1/R-1/i＜n-1 等價于 A＜B＜A·F（i，n）。 那么，A＜A·F（i，n）（A＞0，i＞0，n≥2）的命題是否恒成立呢？答案是肯定的，我們來看以下的詳細證明。 設，其中 i＞0，n≥2。 函數 g（i）對 i求導數，得該導數小于 0，所以 g（i）在 i的定義域（0，+∞）上是單調減函數；又由于當 i→0 時，g（i）的極限為 0，因此，（1+i·n）/移項得兩邊乘 n 次方，得（1+i·n）n-1＜（1+i·n-i）n，故 1＜（1+i·n-i）n/（1+i·n）n-1，因此，A＜A·F（i，n）成立。 又由于債券采用溢價發行方式，故有B＞A。所以，總是能找到滿足條件A＜B＜A·F（i，n）的B值。換言之，對于到期一次還本付息、溢價發行的債券，滿足條件 1/R-1/i＜n-1（R＞0，i＞0，n≥2）的 R 值一定能找到。命題證畢。

三、應用以上公式分別對賀文及王文所提例子進行解釋

賀文所提的例子在前面已給出。例子中，2007年初該債券溢價發行時，已確認“應付債券——利息調整”科目貸方發生額12萬元。在接下來的2007年末、2008年末和2009年末3個資產負債表日，“應付債券——利息調整”科目借方發生額分別為6.4451萬元、4.2460萬元和1.9028萬元，合計12.5939萬元，超過其初始貸方發生額12萬元，出現了賀文中所稱的“利息調整過度”現象，并導致2010年反過來要貸記“應付債券——利息調整”科目0.5939萬元。出現這種現象，是該溢價發行債券的實際利率R為6.5537%或發行價款為512萬元，符合以下條件的結果：（1/6.5537%-1/8%）=2.758556＜（4-1）=3， 或 500＜512＜500×F （8%，4）=513.97。

再來看王文中不會出現利息調整過度現象的例子：2007年1月1日某企業發行債券，面值500萬元，期限4年，年利率9.72%。按單利法計息，到期一次還本付息。該企業溢價發行債券，實際收到發行價款550萬元。該債券到期還本付息金額為：500×（1+9.72%×4）=694.40 （萬元）， 又由694.40×（1+R）-4=550，解得實際利率R為6%。此例沒有出現利息調整過度現象，是該溢價發行債券的實際利率6%或實際收到發行價款550萬元符合以下條件的結果：（1/6%-1/9.72%）=6.378601＞（4-1）=3， 或 550＞500×F （9.72%，4）=519.47。下面，我們為王文的例子找一個滿足條件不等式1/R-1/i＜n-1的R值 （除該例子中實際收到的發行價款外，其他條件不變）。假設王文例子中，實際收到的發行價款不是550萬元，而是510.40萬元（大于面值500萬元，但小于500×F（9.72%，4）=519.47（萬元），則在該債券攤銷溢價的會計核算過程中，必將會出現 “利息調整過度”現象。由694.40×（1+R）-4=510.40，解得實際利率 R 為 8%，符合 1/R-1/i＜n-1不等式，即將相應的數據代入不等式，有 （1/8%-1/9.72%）=2.2119＜（4-1）=3。 修改后，各期的應計利息、實際利息費用、利息調整和攤余成本如表1所示。可以看出，截至2009年年末，“應付債券——利息調整”明細賬的借方累計發生額達到13.243萬元，超過了原記入該明細賬貸方的待攤銷溢價10.4萬元，即出現所謂的“利息調整過度”現象。所以在2010年年末，在“應付債券——利息調整”明細賬記貸方發生額2.843萬元（注：因受所保留的小數位數的影響，本文調整了最后一期的利息調整金額），轉回前述所超金額。

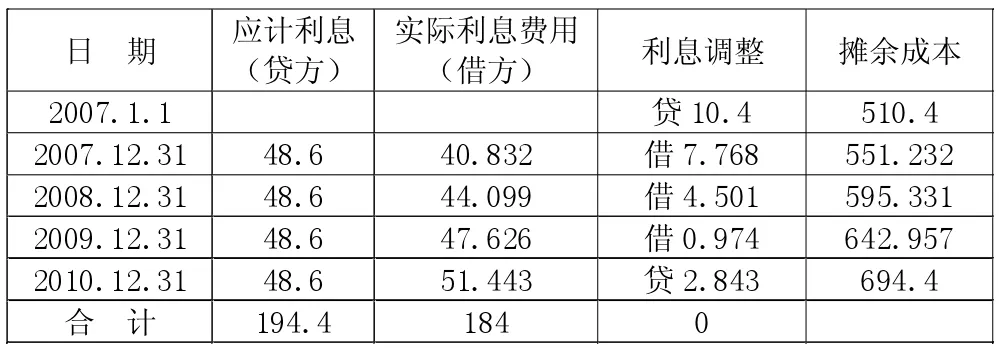
表1 修改后王文例子利息調整計算列表 單位：萬元

四、總結

結合實際利率的定義及上述通過數學證明的條件公式展開具體分析，我們清楚地看到，出現利息調整過度現象的主要原因，不是由于“使用插值法得出的估計實際利率而非真實實際利率”造成的，而是由債券面值、票面利率、債券期限和實際收到的發行價款這些因素在一定條件下產生的結果。