雙排行星齒輪系統的靜態均載特性行為

盛冬平，朱如鵬，靳廣虎，陸鳳霞，鮑和云

?

雙排行星齒輪系統的靜態均載特性行為

盛冬平，朱如鵬，靳廣虎，陸鳳霞，鮑和云

(南京航空航天大學機電學院，江蘇南京，210016)

建立雙排行星齒輪傳動系統的計算模型，并針對其進行靜態均載特性行為的理論研究。模型中考慮各級行星齒輪的偏心誤差，靜態傳遞誤差，時變嚙合剛度等參數，并利用傅里葉級數法求解系統載荷平衡方程。定性地研究行星輪的偏心誤差，齒圈的支撐剛度，行星輪的支撐剛度以及一級行星架的扭轉剛度等參數對系統靜態均載特性行為的影響，并據此得到一些理論分析結果。該研究延伸和擴展了對雙排行星輪系均載特性行為的認識，并為進一步進行動力學均載行為的理論和實驗研究形成一定的基礎，同時也為雙排行星輪系的設計提供一定的 參考。

雙排行星齒輪系；靜態均載；支撐剛度；偏心誤差；扭轉剛度

行星齒輪傳動系統具有空間緊湊、高功率密度以及低噪聲等特性，使得其在實際應用中比平行軸傳動系統具有更廣泛的應用前景。行星輪系包含多個行星輪以用來傳遞和分解作用在輪系中的某一構件上(太陽輪、內齒圈或行星輪)的輸入扭矩，這極大地降低了單對齒輪嚙合對之間的嚙合力，同時也有效地減少了空間的占用。然而，由于系統存在制造誤差、安裝誤差以及磨損等因素，導致作用在每個行星輪上的載荷分布不一致。有關于行星齒輪傳動的均載特性的問題，國內外眾多學者已經進行了大量的理論和實驗研究，也提出了很多新的模型和方法，有些已經得到論證，并應用于工程。Seager[1]提出利用一個簡化的模型來證明浮動的太陽輪對具有3~6個行星輪傳動系統均載性能的重要性。Kahraman[2]構建了一個行星齒輪系的動力學模型，該模型可以用來設定具有任意個數的行星輪，以及任意可能的相應的齒輪尺寸和公差帶，和固定或者浮動的太陽輪，同時針對其提到的相關變量進行了有限的參數化研究。Kahraman[3]利用數學模型和實驗，再次研究了行星齒輪系統的均載特性，并且借助一個含有4個行星輪的實驗來驗證其數學模型。Bodas等[4]利用建立行星輪系的有限元模型來研究各種誤差對均載特性行為的影響，最后，他們根據各種誤差對均載特性的不同影響將其分為3個不同類別。Ligata等[5]在Kahraman[3]研究基礎上進行了進一步的研究，但只是在他們的理論研究中增加了行星輪的個數以及扭矩等參數，且實驗結果和理論分析獲得了一致。Ligata等[6]和Singh[7]提出了一個簡化的模型用來預測行星輪的均載特性。其他的一些理論研究包括Gu等[8]和Montestruc[9]都證實了之前的研究。最新的研究由 Boguski等[10]完成，他們提出一個新的方法來測量行星齒輪系中行星輪的均載和太陽輪的徑向運動軌跡。一些國內外學者還針對行星輪彈性支撐軸進行了理論和實驗研究，認為彈性支撐軸可以改善行星輪系的均載性能。Hicks[11]提出一個新的方法來使行星輪獲得更低的支承剛度，即當行星架是懸臂梁結構時，行星輪的支承可以利用雙懸臂梁銷軸和套筒聯接的結構來降低支承剛度。Fox等[12]進一步擴展了Hicks[11]的方法，他們在銷軸上加工了凹槽來進一步降低行星輪的支承剛度，然而這種設計的代價是提高了銷軸的彎曲應力。后來Fox等[13]在論文中討論了他們的設計，并用實驗研究來證明他們的“彈性銷”設計極大地改善了均載性能，尤其是當行星輪個數越多時效果越好。Montestruc[14]論證了這種設計，并且定量地分析了其優點。國內學者從事行星齒輪的均載特性的研究相對較晚，方宗德等[15]利用Fourier級數方法求解了2K?H型行星減速系統的運動微分方程，并計算了齒輪偏心誤差對齒輪載荷均勻性的影響。肖鐵英等[16]建立了NGW型行星齒輪結構的計算模型，并提出了當量嚙合誤差和等效嚙合剛度的概念。袁茹等[17]定量地描述了不同支承剛度下功率在各行星輪間分配不均衡程度和嚙合動載荷波動程度。陸俊華等[18]建立了2K?H型行星傳動系統的計算模型，從靜力學角度分析了系統的均載機理。葉福明等[19]建立了非等模數非等壓力角NGW型行星齒輪系的靜態均載特性的計算模型，得到一些理論研究結果。盡管國內外眾多學者已經進行了大量的關于行星輪系均載特性的研究，然而到目前為止，幾乎都是針對單排行星齒輪系，尚沒有涉及雙排行星輪系的建模和均載特性研究。為此，本文作者提出一個不考慮動態效應的關于雙排行星輪系的計算模型，系統并定性地分析了包括行星輪偏心誤差，支承剛度，內齒圈的支撐剛度以及一級行星架的扭轉剛度等參數對系統靜態均載特性的影響，并由此得出一些理論結果。

1 雙排行星齒輪系統的建模

1.1 物理模型

雙排行星齒輪系統由兩排獨立的行星輪系組成，并由第1級行星架1和第2級太陽輪2的輸入軸聯接在一起，兩排行星輪系的連接部件(后文稱為中間部件)具有一定的扭轉剛度c1s2，以用來傳遞動力，如圖1所示。第1級的太陽輪1可徑向浮動，行星輪1i和2i由安裝在行星架上的銷軸和軸承來支承，其支承剛度分別為p1和p2。在一些典型的減速器結構中，內齒圈1和2為由長薄壁圓筒支撐，具有一定的支撐剛度r1和r2，以獲得更好的均載特性。原動機的扭轉D作用在1級太陽輪1上，外部負載L作用在2級行星架2的輸出軸上。

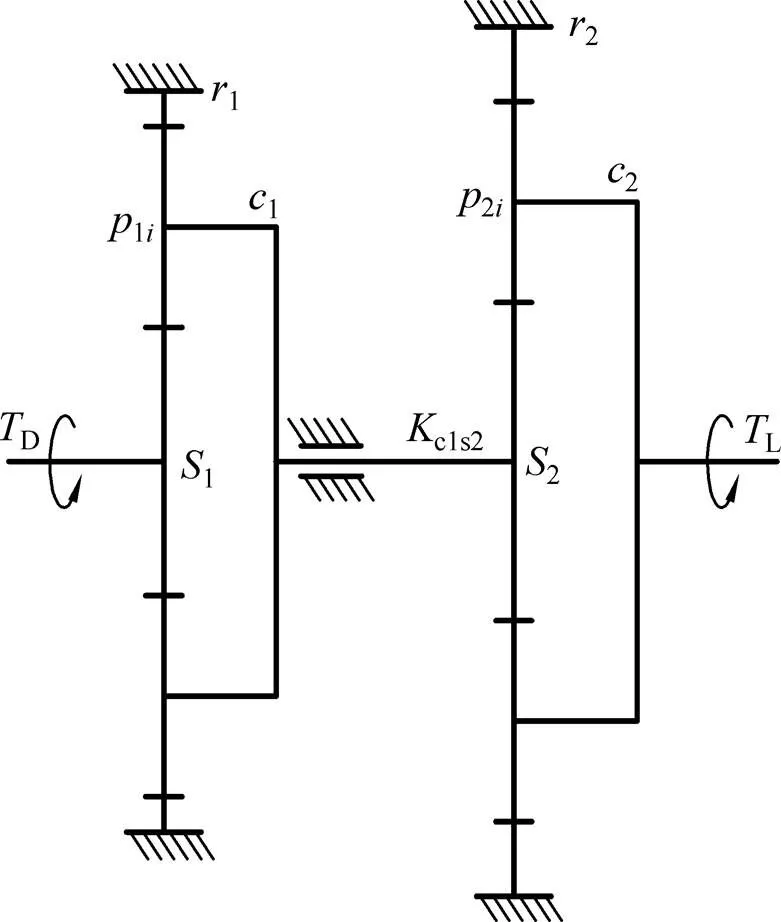
圖1 雙排行星齒輪系統動力傳動原理圖

考慮到第1級和第2級行星輪系間的共同特性，故可利用第1級行星齒輪系統為例來說明雙排行星齒輪系統的自由度，如圖2所示。內齒圈存在彈性支撐，故認為具有2個平動自由度r1和r1，徑向浮動的太陽輪具有3個自由度，包括轉動自由度s1、水平方向位移自由度s1和垂直方向位移自由度s1。行星輪也具有3個自由度，包括繞安裝銷軸的轉動自由度pi、沿著行星輪和太陽輪中心連線方向的位移自由度pi和與之垂直的位移自由度pi。行星架由于安裝軸承對其在徑向位移的限制，使得其只有一轉動自由度c1。另外，盡管第2級行星輪系的太陽不具備徑向浮動能力，但是同樣具有3個自由度，即s2，s2和s2。基于以上分析，在第1級行星輪系有個行星輪和第2級行星輪系具有個行星輪的雙排行星齒輪系統中，共存在12+3(+)個廣義坐標，如下式所示。

式中：i=1，2，…，N；j=1，2，…，M。

1.2 幾何關系

1.2.1 行星輪在嚙合線上的等效偏心誤差

為了便于研究，本文進行簡化處理，假定所有齒輪為標準的漸開線直齒齒輪，不考慮變位系數的影響，忽略軸承的支承間隙和齒輪嚙合副的齒側間隙，同時認為行星架的安裝和制造誤差均包含在行星輪的偏心誤差中[19]。圖3顯示了行星輪系中各齒輪的偏心誤差在太陽輪和行星輪的嚙合線(外嚙合)以及行星輪和內齒圈的偏心誤差在嚙合線(內嚙合)上的等效誤差的幾何關系。由圖3(a)可以得到太陽輪和行星輪分別在外嚙合線上的等效偏心誤差并可以表示為

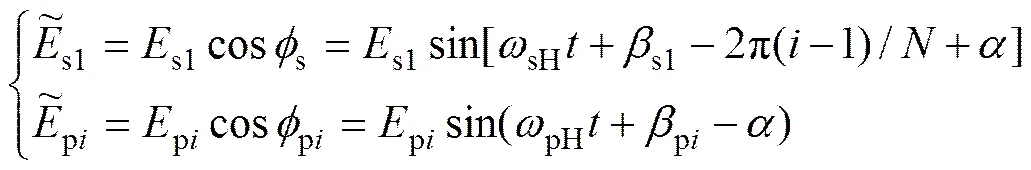
式中：=1，2，…，；和分別為太陽輪和行星輪在外嚙合線上的等效偏心誤差；為太陽輪相對行星架的轉動頻率且等于；為行星輪相對行星架的轉動頻率且等于；為太陽輪的轉動頻率；p和s分別為行星輪和太陽輪的齒數；和分別為太陽輪和行星輪偏心誤差的初始相位角；為齒輪壓力角。

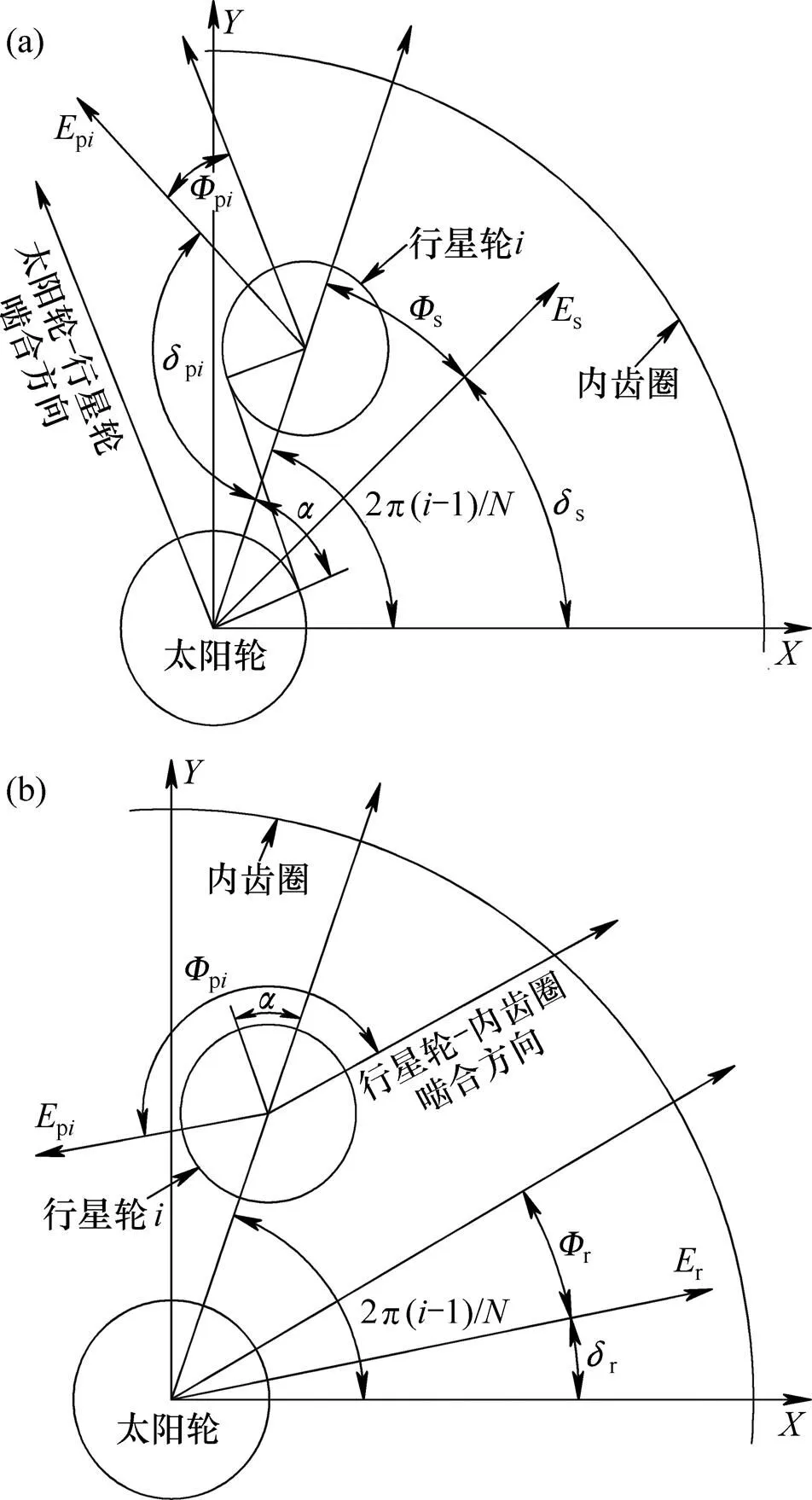
(a) 太陽輪和行星輪的偏心誤差在外嚙合線上等效誤差；(b) 行星輪和內齒圈的偏心誤差在內嚙合線上等效誤差

另外根據圖3(b)所描述的幾何關系，可以得到行星輪和內齒圈的偏心誤差在內嚙合線上的等效誤差和分別為

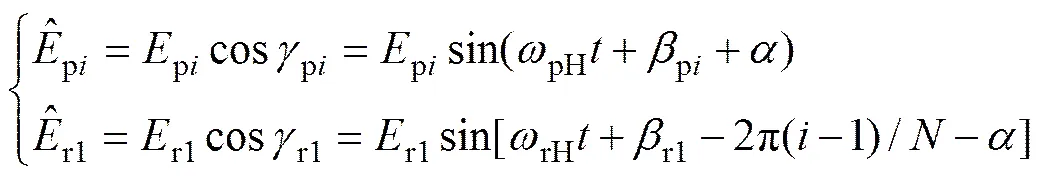
1.2.2 齒輪的平動在嚙合線上的等效位移

由于太陽輪、行星輪和內齒圈存在平動位移，而此位移在一定程度上影響了嚙合副間的彈性嚙合力，故有必要將其分別投影到內外嚙合線上獲得其在嚙合線上的等效位移，從而用于彈性嚙合力的計算。同樣地，取單排行星輪系為例來分析它們之間的幾何關系，根據圖4可以得到各齒輪在各自坐標系中的平動位移在相應嚙合線上的等效位移如下：

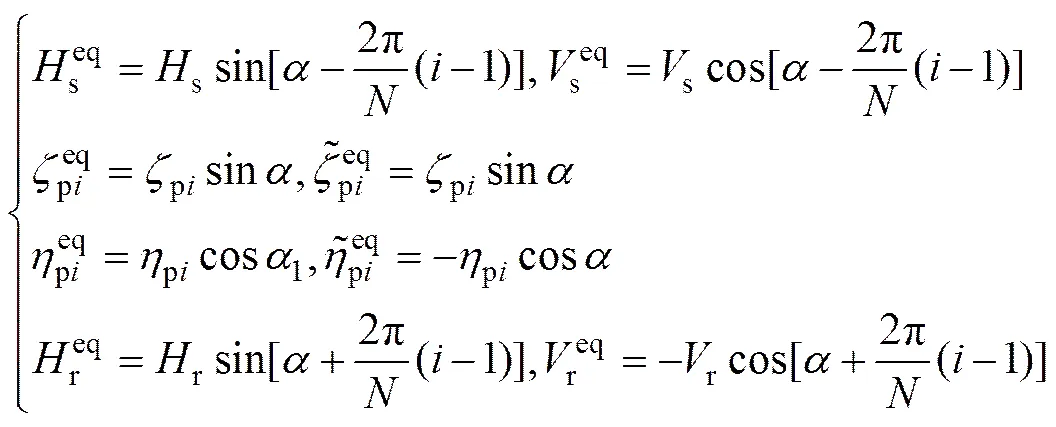
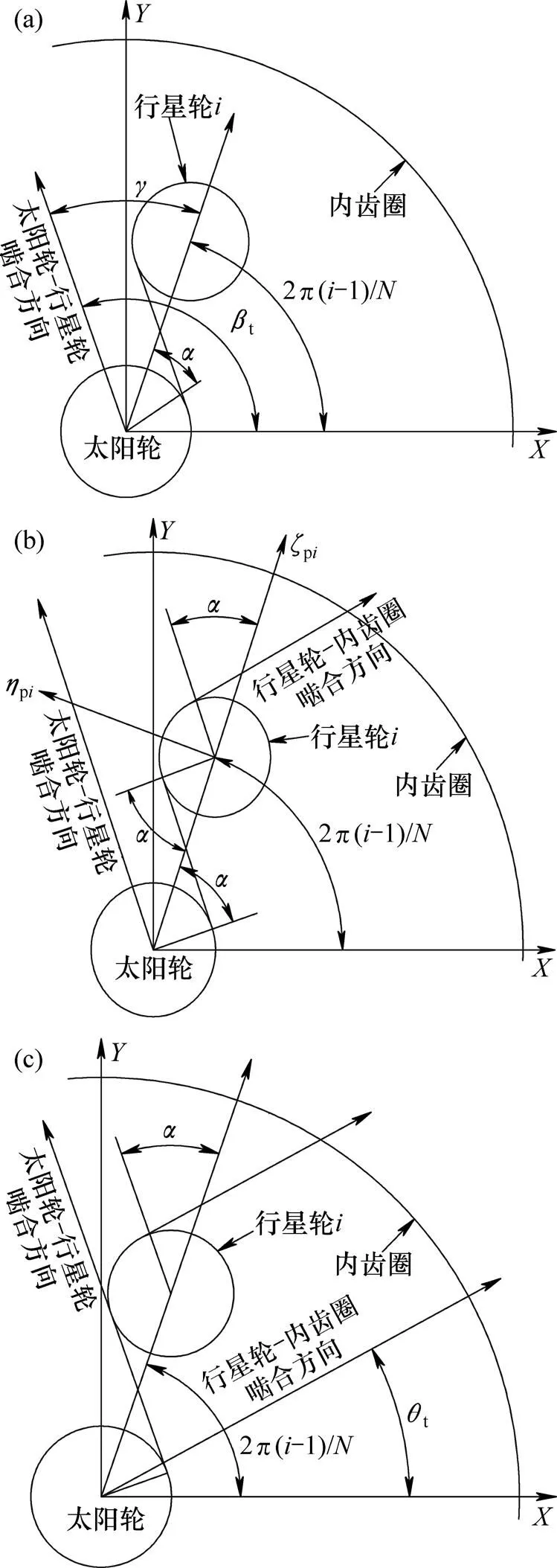
(a) 太陽輪的平動在外嚙合線上的等效位移；(b) 行星輪的平動在內外嚙合線上的等效位移；(c) 行星輪的平動在內外嚙合線上的等效位移

1.3 彈性嚙合力

取單排行星輪系為例來計算輪系中內外各嚙合副間的彈性嚙合力，可由如下公式得到：

式中：=1，2，…，；spi和rpi分別為太陽輪和行星輪以及行星輪和內齒圈之間的彈性嚙合力。spi()和rpi()分別為內外嚙合線上的時變嚙合剛度，可以用傅里葉級數來表示，為簡化計算，此處只取一次基頻諧波項。spi和rpi分別為內外嚙合線上的相對位移，如下式所示：

式中：=1，2，…，；s1和pi分別為太陽輪和行星輪的基圓半徑；spi()和rpi()分別為在外嚙合和內嚙合線上的時變綜合誤差；和為嚙合副間的靜態傳遞誤差[20?21]的幅值；和分別為靜態傳遞誤差的初始相位；為內外嚙合副的嚙合齒頻，并可以證明其等于。

1.4 系統載荷平衡方程

根據如上分析且在不考慮動態效應的情況下，可以推導出雙排行星齒輪系統的靜態載荷平衡方程，如下式所示：

式中：=1，2，…，；=1，2，…，；和分別為第1級和第2級行星輪系的行星輪的支承剛度；r1和r2分別為第1級和第2級輪系內齒圈的支撐剛度；為中間部件的扭轉剛度；s2為第2級輪系中太陽輪的支承剛度；c1和c2分別為第1級和第2級的行星架的等效半徑；s1和s2分別為第1級和第2級的太陽輪的基圓半徑；和分別為第1級和第2級中第個和第個行星輪的基圓半徑；和分別為第1級行星輪系中第個行星輪在內外嚙合線上的彈性嚙合力；和分別為第2級行星輪系中第個行星輪在內外嚙合線上的彈性嚙合力；D和L分別為系統的輸入扭矩和負載扭矩，可通過系統的輸入功率和輸入轉速求得。

2 雙排行星輪系的靜態均載特性的參數研究

為了從實際應用的角度來分析支承剛度和扭轉剛度等系統參數對雙排行星輪系的靜態均載特性的影響，本文從一個真實的齒輪傳動系統中提取出相關參數，如表1所示。另外由于輸入和輸出扭矩的波動取決于原動機和負載，很難消除和測量，因此本文忽略了它們的波動量。方程(6)的解可以通過傅里葉級數法[15]求得，該方法是將系統平衡方程的剛度矩陣、阻尼矩陣和解向量進行定常化，并略去二階小量，最后利用利用線性疊加原理獲得系統的解向量。

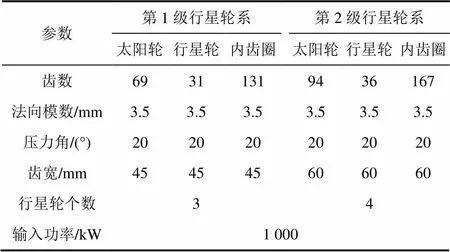
表1 雙排行星齒輪系統的基本結構參數

將方程(6)的解向量代入式(4)，可以得到各級輪系中行星輪在外嚙合副間的嚙合力和，結合兩級行星輪系的輸入扭矩1和2，可以得到各級輪系中單個行星輪的均載系數和為

式中：=1，2，…，；=1，2，…，。

最后可以通過下式分別得到第1級和第2級行星齒輪系統的靜態均載系數[18?19]和：

式中：=1，2，…，；=1，2，…，。

2.1 行星輪的偏心誤差對系統均載特性的影響

圖5顯示了當系統在一組確定的參數下，且相對阻尼比=0.03和輸入轉速=3 000 r/min，第1級和第2級行星輪的偏心誤差在0~80 μm范圍內單獨變化時分別對第1級和第2級行星輪系均載系數的影響。從圖5(a)可以看出：當第1級行星輪的偏心誤差逐漸增加時，第1級輪系的均載系數近似線性地增加了近3%，而第2級輪系的均載系數幾乎保持不變，說明第1級行星輪偏心誤差對第2級輪系均載的影響可以忽略不計。另外，從圖5(b)可以看出：隨著第2級行星輪偏心誤差的增長，第1級輪系的均載系數近似線性增長了3%，而第2級輪系的均載系數則非線性地增長了35%，這表明兩級輪系之間由于第2級行星輪的偏心誤差相關的耦合項產生了一定的耦合作用。比較圖5(a)和5(b)可以看出：在雙排行星輪系的傳動系統中，第2級行星輪的偏心誤差對系統的均載特性影響較大。同時可以判斷出，與第1級行星輪偏心誤差對其自身均載的影響相比，均載系數對第2級行星輪的偏心誤差具有更高的靈敏度。

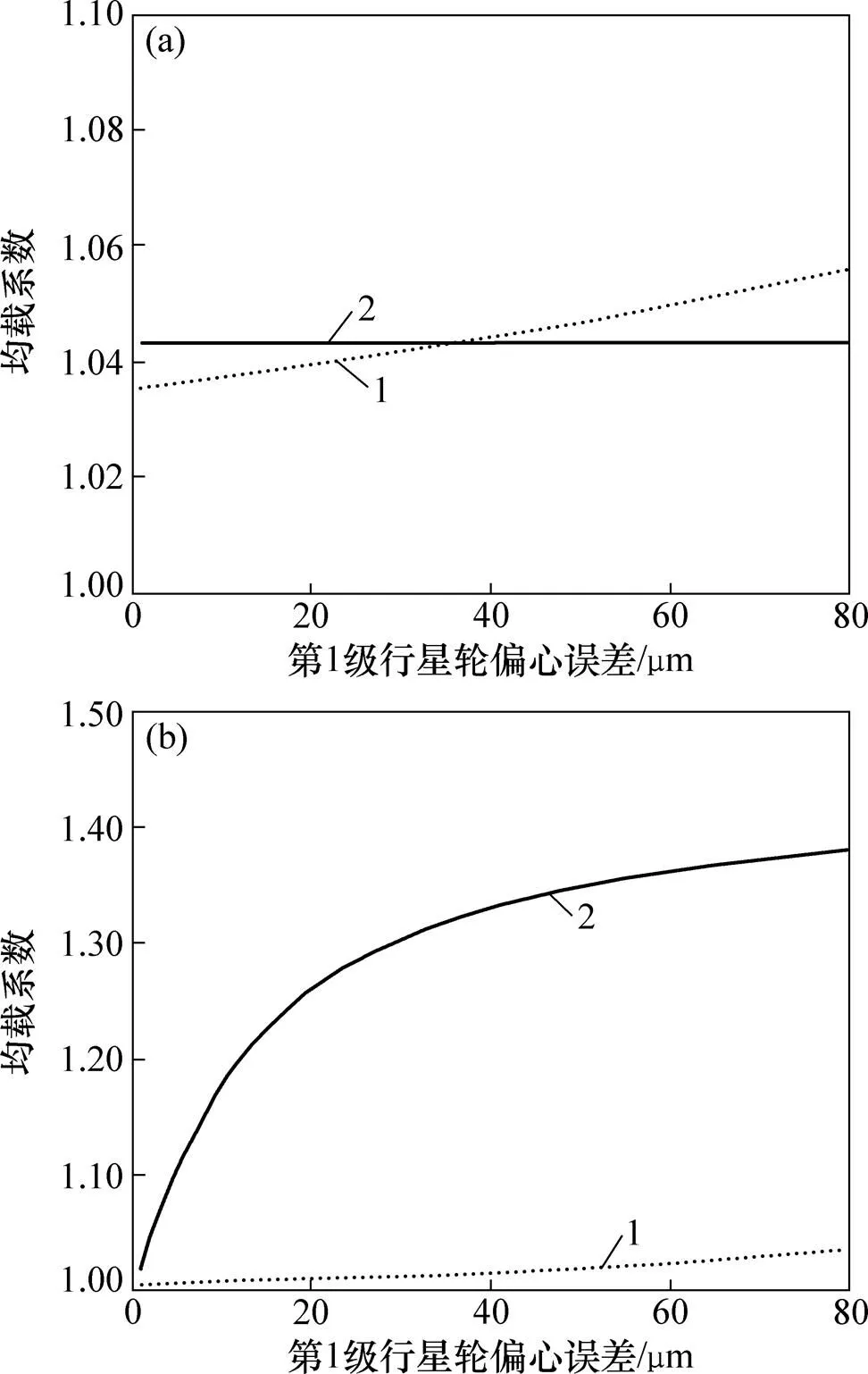
(a) 第1級行星輪偏心誤差單獨變化時第1級和第2級輪系的均載系數；(b) 第2級行星輪偏心誤差單獨變化時第1級和第2級輪系的均載系數

2.2 內齒圈的支撐剛度對系統均載特性的影響

根據現有關于2K?H型行星輪系的均載特性方面的文獻來看，幾乎所有的計算模型都將內齒圈完全固定，不考慮其支撐變形所帶來的影響。然而在一些實際應用中，內齒圈由長薄壁圓柱體支撐，帶有一定的彈性，這種設計被認為對系統的均載性能有一定的改進作用，盡管這種作用到目前為止還沒有在理論和實驗中證實過。為了在理論上驗證這種彈性支撐齒圈的設計對改善均載性能的具體影響，本文通過一個實際算例來說明其作用。圖6顯示了系統在輸入轉速= 3 000 r/min和相對阻尼比=0.03的情況下，系統均載系數隨著各級齒圈支撐剛度單獨變化時的曲線。從 圖6(a)可以看出：當第1級齒圈的支撐剛度從100 MN/m到1 000 MN/m逐漸增加時，第1級輪系的均載系數增加了2%左右，而第2級輪系的均載系數幾乎沒有變化。另外，從圖6(b)可以看出：隨著第2級齒圈的支撐剛度的增長，第1級輪系的均載系數同樣幾乎沒有變化，而第2級輪系的均載系數則大幅增長了15%左右。以上實例分析從理論上證明了彈性支撐齒圈的設計的確可以優化行星輪系的均載性能。另外通過比較圖5和圖6，可以發現一個共同點，即第2級輪系的參數(包括行星輪的偏心誤差和齒圈的支撐剛度)跟第一級輪系的參數相比，其對均載系能的影響更大，靈敏度也更高。經過初步研究，這可能是由于系統本身的結構參數所導致，如第1級和第2級行星輪的個數的不同，以及各級相對應的行星輪、太陽輪，內齒圈的齒數和模數的不同均可能導致該現象，最終結論還需要通過更多的計算實例來進行對比分析得到。

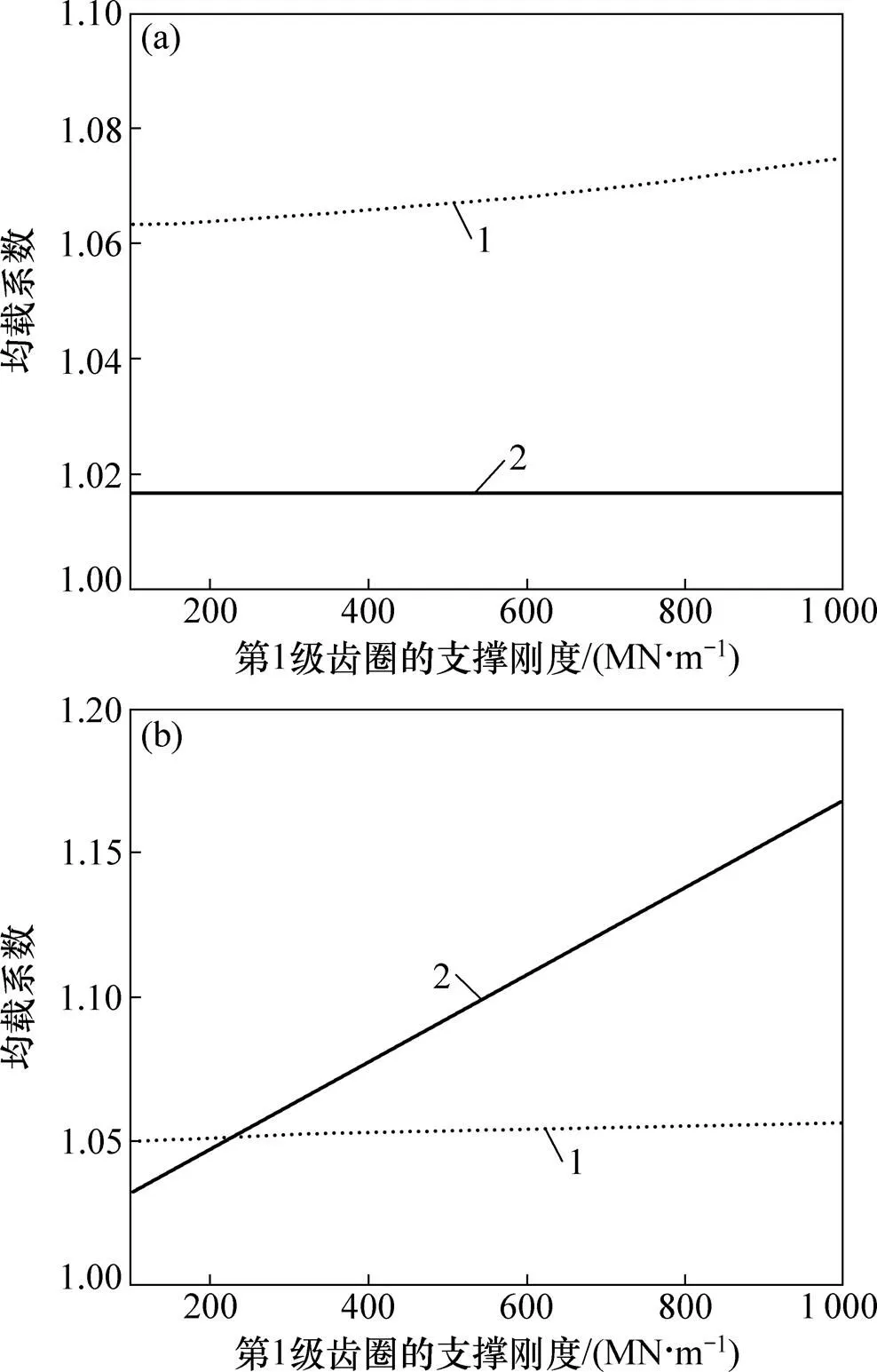
(a) 第1級內齒圈支撐剛度單獨變化時第1級和第2級輪系的均載系數；(b) 第2級內齒圈支撐剛度單獨變化時第1級和第2級輪系的均載系數

2.3 行星輪支承剛度對系統均載特性的影響

圖7顯示了系統在輸入轉速為3 000 r/min以及低阻尼=0.03工況下運行時，當第1級和第2級行星輪的支承剛度從100 MN/m到500 MN/m之間單獨變化時系統各級輪系的均載系數的變化曲線。從圖7(a)可知：隨著第1級行星輪支撐剛度的增加，第1級輪系的均載系數近似線性地增加20%，而第2級輪系的均載系數幾乎沒有變化。但是從圖7(b)可以看出：隨著第2級行星輪的支承剛度的增長，第2級輪系的均載系數則呈現非線性的增長15%，且第1級輪系的均載系數也隨之增長8%，這說明兩級行星輪系之間由于第2級行星輪的支承剛度的影響而存在一定的耦合作用。從圖7(a)和7(b)可以看出：各級行星輪的支承剛度對其所歸屬的行星輪系的均載性能都有著顯著的影響。另外，盡管在一些具體參數未知的情況下，文中2.1和2.3節的計算和分析結果跟現有的關于單對行星輪系的均載特性的理論和實驗研究具有較好的一致性[17, 22?25]，同時這也證明了雙排行星齒輪傳動系統模型的正確性。需要注意的是，雖然從2.2節和2.3節的分析可知，降低內齒圈和行星輪的支承剛度有利于系統均載性能，然而過度提高均載性能將影響結構本身強度和壽命，這需要在設計的過程中綜合考慮行星輪系的各項指標，國外已經有多個針對行星輪支承結構的文獻來討論如何改進設計來降低銷軸的支承剛度以獲得更優的均載性能[11?14]。

(a) 第1級行星輪支承剛度單獨變化時第1級和第2級輪系的均載系數；(b) 第2級行星輪支承剛度單獨變化時第1級和第2級輪系的均載系數

2.4 中間部件的扭轉剛度對系統均載特性的影響

中間部件的扭轉剛度對兩級行星輪系的靜態均載特性有著重要意義。如圖8所示，系統在輸入轉速= 3 000 r/min，相對阻尼比=0.03的工況下，隨著扭轉剛度從20 MN?m/rad增長到80 MN?m/rad，第1級行星輪系的均載系數以緩慢的速度并單調地降低了1%左右，而第2級行星輪系的均載系數則單調地增長了8%。可以明顯地看出中間部件的扭轉剛度對第1級行星輪系的均載系數影響較弱，而對第2級行星輪系的均載系數影響較大。另外，由于兩級行星輪系的均載系數的特性曲線具有不同的單調性(第1級輪系單調減小，第2級輪系單調增大)，這意味著必有一平衡點存在，且通過多個算例證明該平衡點是普遍存在的，并不僅僅限于某一特殊的參數條件，這意味著在實際的雙排行星齒輪系統的設計中，當考慮扭轉剛度對各級輪系的均載特性的影響時，對該平衡點的分析和控制顯得尤其重要。

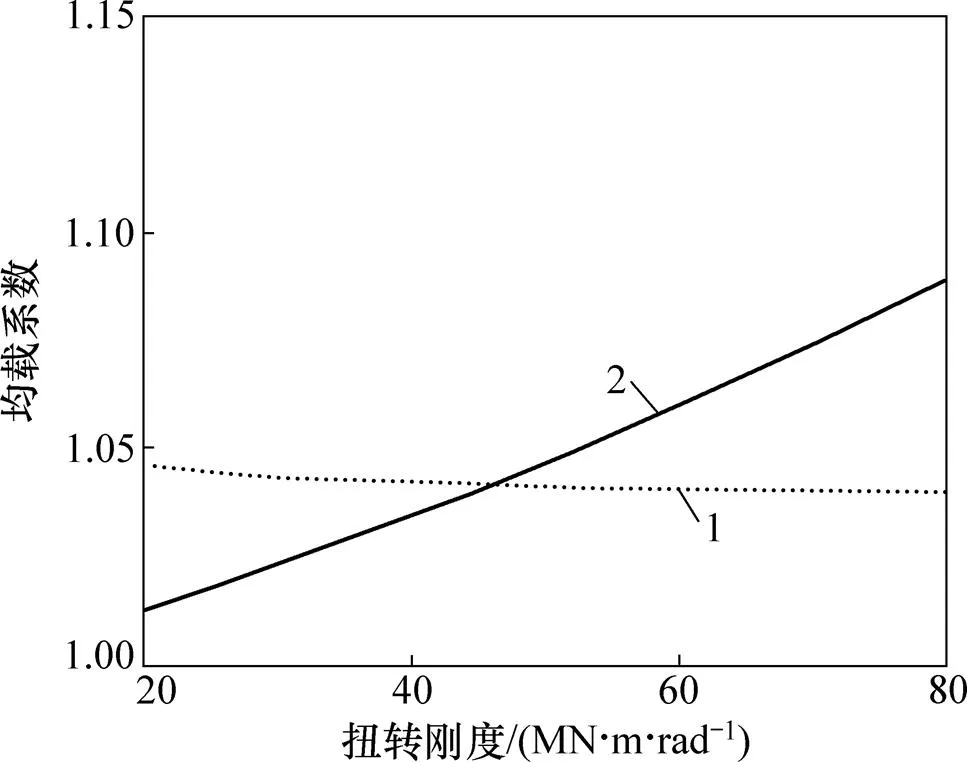
1—第1級行星輪系；2—第2級行星輪系

3 結論

1) 建立了雙排行星輪系傳動系統的靜力學均載計算模型，模型中考慮了時變嚙合剛度、行星輪支承剛度、中間部件的扭轉剛度和靜態傳遞誤差等參數，并針對該模型進行了靜態均載特性的參數研究。

2) 第1級和第2級輪系中的行星輪偏心誤差對系統的靜態均載特性有較大影響，且兩級行星輪系之間通過該參數存在一定的彈性耦合。

3) 從理論上證明了兩級輪系中內齒圈的彈性支撐設計能夠改善系統的均載性能，且通過降低第2級內齒圈的支撐剛度對改善靜態均載性能的貢獻更大。

4) 行星輪的支承剛度對系統靜態均載特性有顯著的影響，且第2級行星輪的支承剛度對其均載的影響更明顯，其變化對均載系數也更敏感，同時兩級輪系之間通過該參數存在較弱的耦合效應。

5) 中間部件的扭轉剛度對第1級輪系的靜態均載特性影響較小，而對第2級輪系的均載影響則較大。第1級和第2級輪系的靜態均載特性曲線上的平衡點對雙排行星齒輪的設計具有指導意義。

[1] Seager D L. Load sharing among planet gears[C]//SAE Paper. Warrendale: SAE International, 1970: 700178.

[2] Kahraman A. Load sharing characteristics of planetary transmission[J]. Mech Mach Theory, 1994, 29: 1151?1165.

[3] Kahraman A. Static load sharing characteristics of transmission planetary gear sets: Model and experiment[J]. SAE Trans, 1999, 108(6): 1954?1963.

[4] Bodas A, Kahraman A. Influence of carrier and gear manufacturing errors on the static planet load sharing behavior of planetary gear sets[J]. JSME Int J Ser C, 2004, 47(3): 908?915.

[5] Ligata H, Kahraman A, Sing A. An experimental study of the influence of manufacturing errors on planetary gear stresses and planet load sharing[J]. Journal of Mechanical Design, 2008, 130: 041701.

[6] Ligata H, Kahraman A, Singh A. A closed-form planet load sharing formulation for planetary gear sets using a translational analogy[J]. Journal of Mechanical Design, 2009, 131: 021007.

[7] Singh A. Load sharing behavior in epicyclic gears: Physical explanation and generalized formulation[J]. Mech Mach Theory, 2010, 45: 511?530.

[8] Gu X, Velex P. A lumped parameter model to analyze the dynamic load sharing in planetary gears with planet errors[J]. Appl Mech Mater, 2011, 86: 374?379.

[9] Montestruc A N. Influence of planet pin stiffness on load sharing in planetary gear trains[J]. Journal of Mechanical Design, 2011, 133: 014501.

[10] Boguski B, Kahraman A, Nishino T A. New method to measure planet load sharing and sun gear radial orbit of planetary gear sets[J]. Journal of Mechanical Design, 2012, 134: 071002.

[11] Hicks R J. Load equalizing means for planetary pinions: US, 3303713[P]. 1967.

[12] Fox G P, Jallat E. Epicyclic gear system: US, 6994651[P]. 2006.

[13] Fox G P, Jallat E. Use of the integrated flexpin bearing for improving of the performance of epicyclical gear systems[EB/OL]. [2008]. http://www.timken.com/enus/solutions/ energy/indenergy/Documents/FlexpinBearingPaper.pdf.

[14] Montestruc Aalfred N. A numerical approach to calculation of load sharing in planetary gear drives[J]. Journal of Mechanical Design, 2010, 132: 014503.

[15] 方宗德, 沈允文, 黃鎮東. 2K-H行星減速器的動態特性[J]. 西北工業大學學報, 1990, 8(4): 361?371. FANG Zongde, SHEN Yunwen, HUANG Zhendong. Analysis of dynamic behaviour of 2k-h planetary gearing[J]. Journal of Northwestern Polytechnical University, 1990, 8(4): 361?371.

[16] 肖鐵英, 袁盛治, 陸衛杰. 行星齒輪機構均載系數的計算方法[J]. 東北重型機械學院學報, 1992, 16(4): 290?295. XIAO Tieying, YUAN Shengzhi, LU Weijie. Calculative method of load balance coefficient in planetary gear[J]. Journal of Northeast Heavy Machinery Institute, 1992, 16(4): 290?295.

[17] 袁茹, 王三民, 沈允文. 行星齒輪傳動的動率分流動態均衡優化設計[J]. 航空動力學報, 2000, 15(4): 410?418. YUAN Ru, WANG Sanmin, SHEN Yunwen. Dynamic optimum design of power shared out equally among the planetary gears[J]. Journal of Aerospace Power, 2000, 15(4): 410?418.

[18] 陸俊華, 李斌, 朱如鵬. 行星齒輪傳動靜力學均載分析[J]. 機械科學與技術, 2005, 24(6): 702?705. LU Junhua, LI Bin, ZHU Rupeng. Analysis of static load sharing in planetary gearing[J]. Mechanical Science and Technology, 2005, 24(6): 702?705.

[19] 葉福民, 朱如鵬, 鮑和云. 非等模數非等壓力角NGW型行星齒輪系靜力學均載行為[J]. 中南大學學報(自然科學版), 2011, 42(7): 1960?1966. YE Fumin, ZHU Rupeng, BAO Heyun. Static load sharing behavior in ngw planetary gear train with unequal modulus and pressure angles[J]. Journal of Central South University (Science and Technology), 2011, 42(7): 1960?1966.

[20] Houser D R. Gear noise state of the art[C]//Proceedings of Inter-Noise. Avignon, France, 1988: 601?606.

[21] Kahraman A, Singh A. Non-linear dynamics of a spur gear pair[J]. Journal of Sound and Vibration, 2009, 142(1): 49?75.

[22] Singh A, Kahraman A, Ligata H. Internal gear strains and load sharing in planeteary transmissions-model and experiments[J]. Journal of Mechanical Design, 2008, 130(7): 0726002.

[23] 孫智民, 沈允文, 李素有. 封閉行星齒輪傳動系統的動態特性研究[J]. 機械工程學報, 2002, 38(2): 44?48. SUN Zhimin, SHEN Yunwen, LI Suyou. Study on dynamic behavior of encased differential gear train[J]. Chinse Journal of Mechanical Engineering. 2002, 38(2): 44?48.

[24] 鮑和云, 朱如鵬. 兩級星型齒輪傳動靜力學系統基本浮動構件浮動量分析[J]. 中南大學學報(自然科學版), 2006, 37(3): 553?557. BAO Heyun, ZHU Rupeng. Floating displacement static analysis of basic floating part of 2-stages star gear train[J]. Journal of Central South University (Science and Technology), 2006, 37(3): 553?557.

[25] 陸俊華, 朱如鵬, 靳廣虎. 行星傳動動態特性分析[J]. 機械工程學報, 2009, 45(5): 85?90. LU Junhua, ZHU Rupeng, JIN Guanghu. Analysis of dynamic load sharing behavior in planetary gearing[J]. Journal of Mechanical Engineering, 2009, 45(5): 85?90.

Static load sharing behavior of double-row planetary gear train

SHENG Dongping, ZHU Rupeng, JIN Guanghu, LU Fengxia, BAO Heyun

(College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

A new model for analyzing the static load sharing characteristics of double-row planetary gear set was proposed, and planet’s eccentricity error, static transmission error, and time-varying meshing stiffness were taken into consideration. The equilibrium equations were determined by the method of Fourier series, and the behavior of static load sharing characteristics affected by the system parameters including gear eccentricity error, ring gear’s supporting stiffness, planet’s bearing stiffness and torsional stiffness of first stage carrier were investigated quantitatively. Theoretical analysis extends our current understanding of behavior of static load sharing characteristics, forms the basis of further theoretical and experimental research, and provides guidelines for the designing of the double-row planetary gear transmission system.

double-row planetary gear; static load sharing; supporting stiffness; eccentricity error; torsional stiffness

10.11817/j.issn.1672-7207.2015.10.012

TH132

A

1672?7207(2015)10?3637?09

2015?02?22；

2015?05?17

國家自然科學基金資助項目(51375226)；高等學校博士學科點專項科研基金資助項目(20113218110017)；江蘇省高校優秀學科建設工程資助項目(PAPD)；江蘇省研究生創新基金資助項目(CXZZ11_0199)；中央高校基本科研業務費專項資金資助項目(NZ2013303，NZ2014201)(Project (51375226) supported by the National Natural Science Foundation of China; Project (20113218110017) supported by the Doctoral Program Foundation of Institutions of Higher Education of China; Project (PAPD) supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions, China; Project (CXZZ11_0199) supported by the Funding of Jiangsu Innovation Program for Graduate Education, China; Projects (NZ2013303, NZ2014201) supported by the Fundamental Research Funds for the Central)

朱如鵬，博士，教授，從事齒輪傳動系統的動力學研究；E-mail：rpzhu@nuaa.edu.cn

(編輯 陳愛華)