基于因素分布模型的微震定位精度敏感性分析

高永濤，吳慶良，吳順川，楊凱，豆麗萍，姚鵬飛

?

基于因素分布模型的微震定位精度敏感性分析

高永濤，吳慶良，吳順川，楊凱，豆麗萍，姚鵬飛

(北京科技大學(xué)土木與環(huán)境工程學(xué)院，金屬礦山高效開采與安全教育部重點(diǎn)實(shí)驗(yàn)室，北京，100083)

根據(jù)微震定位方程，基于誤差最小原理，構(gòu)造微震定位精度敏感性評(píng)價(jià)的輸入輸出數(shù)學(xué)模型，選取震源點(diǎn)到各檢波器之間距離測(cè)量誤差、微震波波速標(biāo)定誤差和信號(hào)到時(shí)拾取誤差3個(gè)影響因素作為分析因子。從信息熵的角度，分析因素分布密度函數(shù)，并通過泛函變分求得相應(yīng)表達(dá)式。采用正交法設(shè)計(jì)16組方案，根據(jù)分布函數(shù)求取因素各水平值，進(jìn)行全局敏感性分析。研究結(jié)果表明：3個(gè)因子取值在給定區(qū)間內(nèi)均符合均勻分布；無論是對(duì)內(nèi)場震源點(diǎn)還是外場震源點(diǎn)，微震波波速誤差，是對(duì)定位結(jié)果影響最大的因素，各因子對(duì)定位精度影響的主次順序?yàn)椋篹，e，e；對(duì)于內(nèi)場震源點(diǎn)，3個(gè)因素對(duì)定位精度均有高度顯著影響。但對(duì)于外場震源點(diǎn)，可能由于因素之間的交互作用或者試驗(yàn)誤差影響，僅微震波波速標(biāo)定誤差對(duì)定位精度有高度顯著影響。相關(guān)研究可為微震監(jiān)測(cè)的準(zhǔn)確定位等提供針對(duì)性指導(dǎo)。

微震；定位精度；敏感性；分布模型；誤差

隨著深部礦產(chǎn)資源的采掘和地下空間的開發(fā)利用，地下工程不斷走向深部，特別是非煤礦山及隧道工程，高應(yīng)力條件下巖爆、地質(zhì)缺陷活化等問題日漸突出，單純靠傳統(tǒng)的巖石力學(xué)手段已經(jīng)遠(yuǎn)遠(yuǎn)不能滿足現(xiàn)實(shí)安全監(jiān)測(cè)的需要，基于地球物理學(xué)發(fā)展起來的微震技術(shù)可以有效的監(jiān)測(cè)巖石微破裂發(fā)生的位置，近年來，已經(jīng)廣泛地應(yīng)用于礦山、水電等地下工程監(jiān)測(cè)[1?3]。微震事件的空間分布規(guī)律包含著巖體不穩(wěn)定區(qū)域的位置、范圍和方向等大量信息，然而由于實(shí)際工程的復(fù)雜多樣，造成定位結(jié)果會(huì)出現(xiàn)不同程度的誤差，少則幾米，多則數(shù)十米。影響微震定位精度的因素較多，且大部分具有隨機(jī)性、可變性、模糊性等不確定特點(diǎn)，要進(jìn)行準(zhǔn)確可靠的定量分析較為困難，因此，對(duì)影響定位精度的根本因素進(jìn)行敏感性分析十分必要。目前用于因素敏感性分析的方法很多，按考慮影響因素多少可分為單因素分析法(局部敏感性分析)和多因素分析法(全局敏感性分析)。單因素分析法只檢驗(yàn)單個(gè)因素對(duì)模型的影響程度，計(jì)算簡單快捷，但需要一定的假設(shè)，與實(shí)際情況不符，代表性的研究有Garson算 法[4]、隨機(jī)檢驗(yàn)法[5]等；而多因素分析法可檢驗(yàn)多個(gè)因素對(duì)模型結(jié)果產(chǎn)生的總影響，并考慮了因素之間的相互作用對(duì)模型輸出的影響，更符合實(shí)際情況，在橋 梁、結(jié)構(gòu)、經(jīng)濟(jì)、水文、環(huán)境、生態(tài)等領(lǐng)域得到廣泛應(yīng)用[6?12]，代表性的研究有方差分解法[10]、偏導(dǎo)數(shù)(PaD2)法[11]，拉丁超立方單因子每次(LH-OAT)方 法[12]。由于敏感性分析在一定的輸入輸出模型和因素分布模型基礎(chǔ)上進(jìn)行的，因此，本文作者根據(jù)微震定位方程，基于誤差最小原理構(gòu)造相應(yīng)的輸入輸出數(shù)學(xué)模型，并從信息熵的角度分析因素分布密度函數(shù)，最后采用正交設(shè)計(jì)法進(jìn)行全局敏感性分析，找出相應(yīng)的較敏感因素和最敏感因素。本文作者的研究可為微震監(jiān)測(cè)的準(zhǔn)確定位等提供針對(duì)性指導(dǎo)。

1 輸入輸出模型的建立

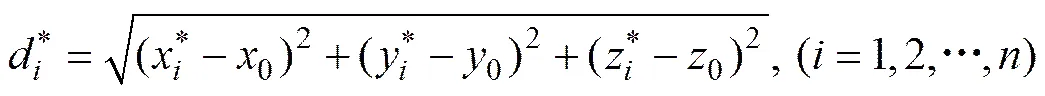
若發(fā)震時(shí)間為0，檢波器接收到信號(hào)的時(shí)間為，震源到各檢波器之間巖層中的微震波傳播速度(均勻速度模型)為，則定位方程為

從式(2)可以看出：礦山現(xiàn)場地質(zhì)地形復(fù)雜、資源開采時(shí)人類活動(dòng)干擾等原因?qū)ξ⒄鹗录ㄎ痪鹊挠绊懽罱K體現(xiàn)在3個(gè)方面：震源點(diǎn)到各檢波器之間距離的測(cè)量誤差(即檢波器坐標(biāo)測(cè)量誤差)、微震波波速標(biāo)定誤差、信號(hào)到時(shí)拾取誤差。假定參數(shù)測(cè)量值與真值之間誤差為(=1, 2, …,;=1, 2, 3)，則

將式(3)代入定位方程可得：

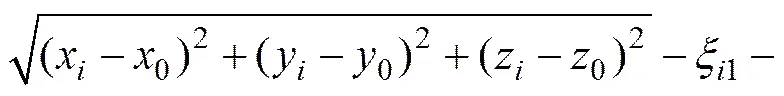
(4)

2 影響因素分布密度函數(shù)

為分析微震定位精度對(duì)相關(guān)參數(shù)的敏感程度，選取震源點(diǎn)到各檢波器之間的距離測(cè)量誤差D、微震波波速標(biāo)定誤差V和信號(hào)到時(shí)拾取誤差T這3個(gè)因素作為分析因子。假定在某次微震事件定位分析過程中，某個(gè)因子值有種可能，且它們出現(xiàn)的概率分別為，則這個(gè)因子的熵為

若測(cè)量誤差值有無窮多個(gè)可能，且連續(xù)分布，則熵可寫為

求極限可得

假定某個(gè)因子只可能出現(xiàn)在有限區(qū)域[,]內(nèi)，則限制條件記為。由于事先無法準(zhǔn)確預(yù)測(cè)該因子取值，即不確定性最大，則對(duì)應(yīng)的熵應(yīng)為極值，對(duì)熵變分，則有。

定義函數(shù)

使其滿足歐拉方程

通過限制條件，求得

顯然某個(gè)因子取值在給定區(qū)間內(nèi)符合均勻分布，式(13)為均勻分布的一般表達(dá)式。

3 因子各水平取值及試驗(yàn)方案的優(yōu)化設(shè)計(jì)

在全局敏感性分析中，若對(duì)每個(gè)因素的每個(gè)水平都相互搭配進(jìn)行全面分析，則隨著因素和水平數(shù)的增加，處理組合數(shù)將急劇增加，必然會(huì)耗費(fèi)大量的時(shí)間、人力和物力。大量研究表明：在全部處理組合中，采用正交設(shè)計(jì)方法，僅挑選部分有代表性的水平組合(處理組合)進(jìn)行分析，同樣能達(dá)到理想結(jié)果。

若某個(gè)因子值的分布區(qū)間為[,]，分布密度函數(shù)為，選取個(gè)水平將該分布密度函數(shù)曲線下的全部面積做?1等分，算上頭尾區(qū)間，則相應(yīng)的積分上限即為各水平值，即

采用3因素4水平L16(45)進(jìn)行正交設(shè)計(jì)。正交試驗(yàn)設(shè)計(jì)方案如表1所示。

表1 正交試驗(yàn)設(shè)計(jì)方案

4 算例分析

假定在空間區(qū)域內(nèi)，6個(gè)傳感器位于球體的6個(gè)方位點(diǎn)，坐標(biāo)(單位均為m)分別是(0，500，500)，(500，0，500)，(1 000，500，500)，(500，1 000，500)，(500，500，1 000)和(500，500，0)。假定微震源(232，604，746)和(673，700，1 200)分別位于檢波器陣列的內(nèi)、外場區(qū)域，微震波在介質(zhì)中傳播的等效波速=5.2 m/ms，發(fā)震時(shí)間統(tǒng)一為某日10:00:00:20，傳感器與震源空間分布位置如圖1所示，本文規(guī)定在某1次微震事件中，外界對(duì)單一因素造成的誤差相等。

選用北京科技大學(xué)自主研發(fā)的微地震監(jiān)測(cè)系統(tǒng)(BMS)作為監(jiān)測(cè)設(shè)備，對(duì)河北某礦山進(jìn)行1 a多的微震監(jiān)測(cè)[13]統(tǒng)計(jì)發(fā)現(xiàn)，震源點(diǎn)到各檢波器之間的距離測(cè)量誤差D(m)、微震波波速標(biāo)定誤差V(m/ms)和信號(hào)到時(shí)拾取誤差T(ms)這3個(gè)因子的分布區(qū)間分別為[0, 6]，和[0, 3]，參照因素各水平的求解方法和正交試驗(yàn)方案，可得內(nèi)、外場震源點(diǎn)的3因素4水平值如表2所示。

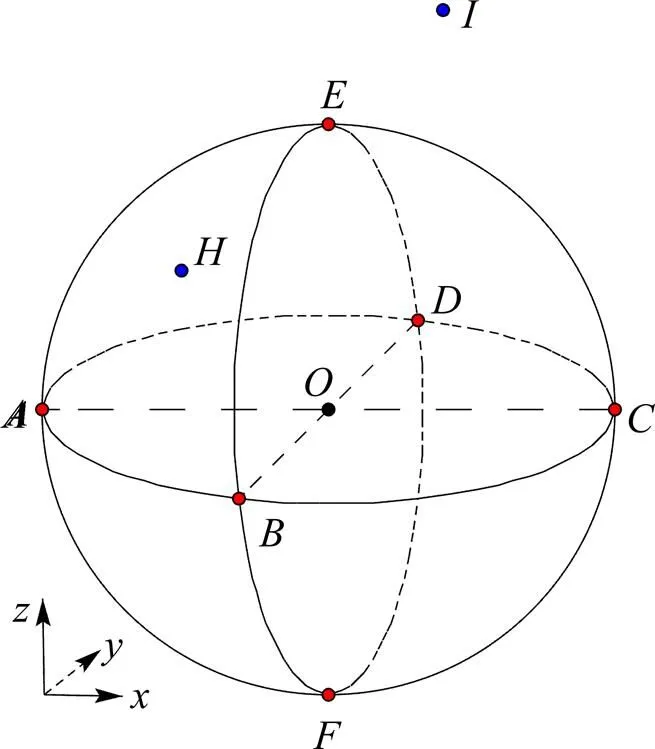
圖1 傳感器與震源空間分布位置示意圖

最終求得內(nèi)、外場震源點(diǎn)的定位結(jié)果(各16組)，如表3所示。

5 敏感性分析

根據(jù)表3所示的定位結(jié)果，分別采用直觀分析方法和方差分析法對(duì)影響微震定位精度的3個(gè)因素進(jìn)行敏感性分析。設(shè)試驗(yàn)次數(shù)為，每個(gè)因素的水平數(shù)為個(gè)，每個(gè)水平作/(即次)試驗(yàn)。

5.1 直觀分析(極差分析)

表4所示為內(nèi)場震源點(diǎn)試驗(yàn)結(jié)果的極差分析，表5所示為外場震源點(diǎn)試驗(yàn)結(jié)果的極差分析。表4和表5中：K為第列因素水平所對(duì)應(yīng)的試驗(yàn)指標(biāo)的和；為K的平均值；R為第列因素的極差，反映了第列因素的水平變動(dòng)時(shí)，定位精度的變動(dòng)幅度。根據(jù)極差R，可以判斷因素的主次。

從表4和表5可知：各列的極差不相等，這說明各因素的水平改變對(duì)定位精度的影響不相同，R越大，表示該列因素的數(shù)值在試驗(yàn)范圍內(nèi)的變化會(huì)導(dǎo)致定位精度在數(shù)值上變化越大，所以，極差最大的那1列即微震波波速誤差，對(duì)定位結(jié)果影響最大的因素，也就是最主要的因素。由于內(nèi)場和外場震源點(diǎn)試驗(yàn)結(jié)果的極差R從大到小的順序均為V，T，D，故各因素從主到次的順序?yàn)椋?i>V，T，D。

相對(duì)各因子列(第1，2和3列)，空白列(第4列)的水平均值隨著水平數(shù)的改變而變化(變化很小)，說明因素之間有一定的交互作用，或試驗(yàn)有一定的試驗(yàn)誤差影響(外場震源定位結(jié)果較為明顯)。但由于其極差小于各因素列的極差，故而本算例中暫不考慮其影響。

表2 正交設(shè)計(jì)時(shí)內(nèi)、外場震源點(diǎn)的3因素4水平值

表3 內(nèi)、外場震源點(diǎn)的定位結(jié)果

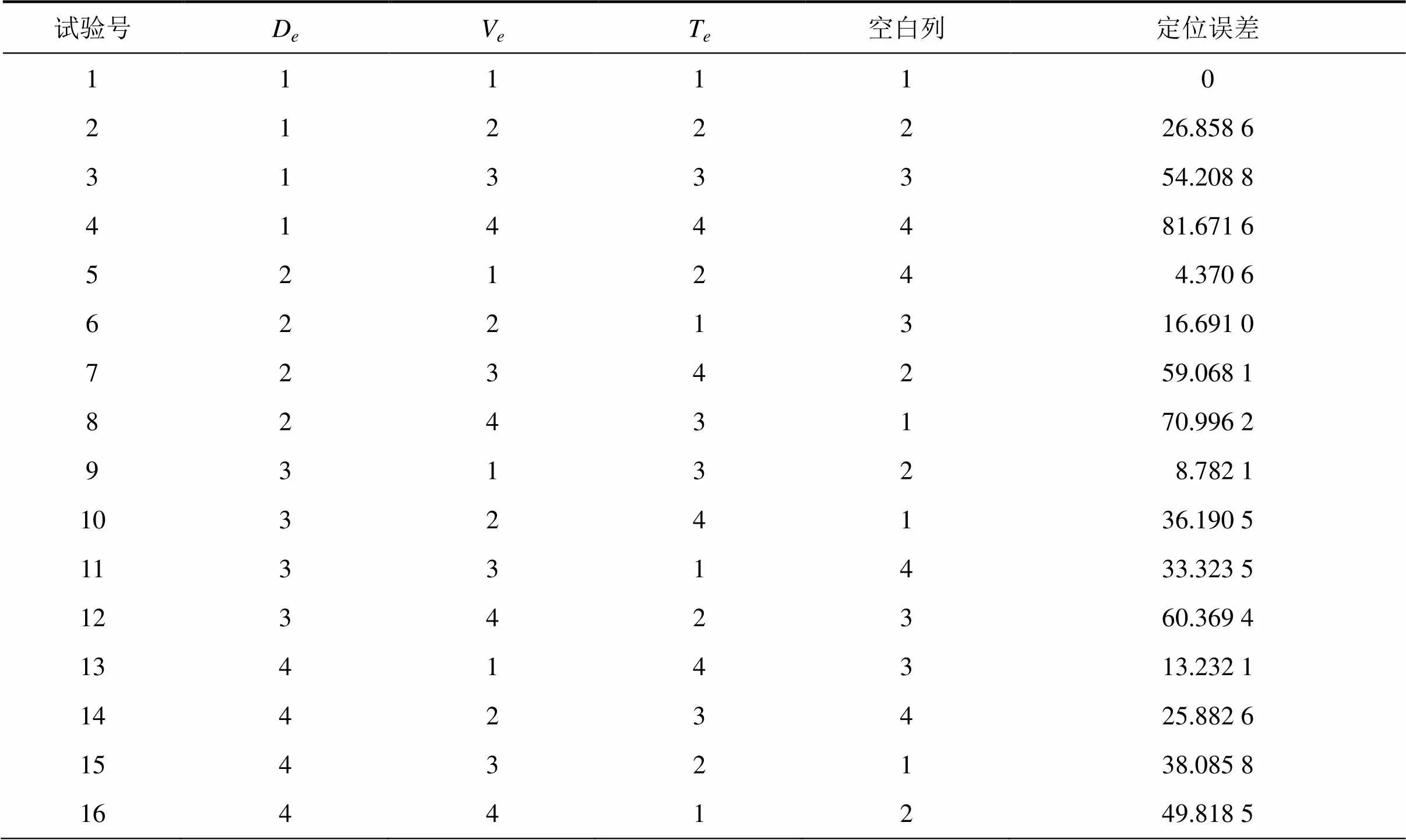
表4 內(nèi)場震源點(diǎn)試驗(yàn)結(jié)果的極差分析