Fourier分析中的幾個核函數研究

王志珍

（上海師范大學數理學院，上海 200234）

Fourier分析中的幾個核函數研究

王志珍

（上海師范大學數理學院，上海 200234）

研究Fourier分析中的Dirichlet核函數、Fejér核函數和Poisson核函數，介紹優核的概念.證明Dirichlet核函數不是優核，Fejér核函數和Poisson核函數是優核.

優核；Dirichlet核函數；Fejér核函數；Poisson核函數

1　引言

Fourier分析是分析領域的重要基礎和組成部分，隨著數學與科技的不斷發展，Fourier分析也在越來越多的領域展示出其重要性.Fourier分析既可以應用于純數學領域（如數論）［1］，又是應用數學領域（如信號與圖像處理）的重要工具［2］.文獻［3-4］通過構建基于Fourier分析的濃度動量法對濕地環境進行研究，得到濕地灘涂流的解析解，從而給出濕地環境彌散現象的細節描述.

給定一以2π為周期的可積函數f（x），其Fourier級數展開為：

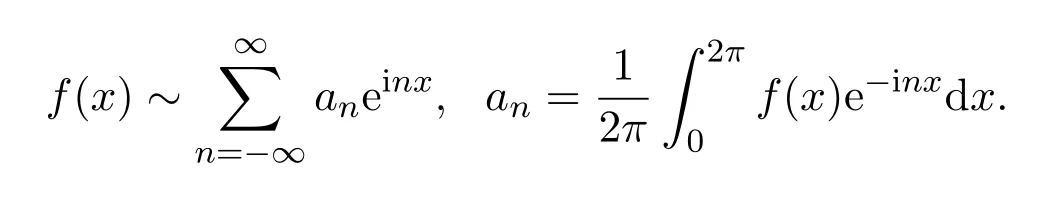
一個自然的問題是：如果f（x）在某一點x處連續，其Fourier級數能否在這一點收斂到f（x）？更進一步，如果f（x）處處連續，其Fourier級數能否一致收斂到f（x）？實際上關于Fourier級數收斂性的研究很早就開始了，早在十九世紀，Dirichlet就給出了著名的Dirichlet收斂定理［5］，但其結果只是針對Fourier級數常規求和而言的.如果只考慮常規求和，一個連續函數的Fourier級數展開甚至可能不收斂.Zygmund曾構造出一個在區間［-π，π］連續的函數，但其Fourier級數在［-π，π］上可列個點處發散的例子［6］.之后人們注意到級數的求和方法可以不拘泥于常規求和，并引入Cesàro求和與Abel求和以豐富級數求和理論.文獻［7］研究了這三種求和方式優缺點，指出常規求和適用范圍最小，Abel求和適用范圍最廣.本文將通過改變Fourier級數的求和方式并引入相應的核函數概念，研究Fourier級數在不同求和方式下其收斂性會有哪些有趣的結果.

2　核函數概念

定義Dirichlet核函數如下：

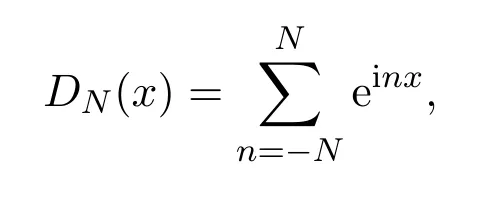
則f（x）的Fourier級數的部分和可寫為：

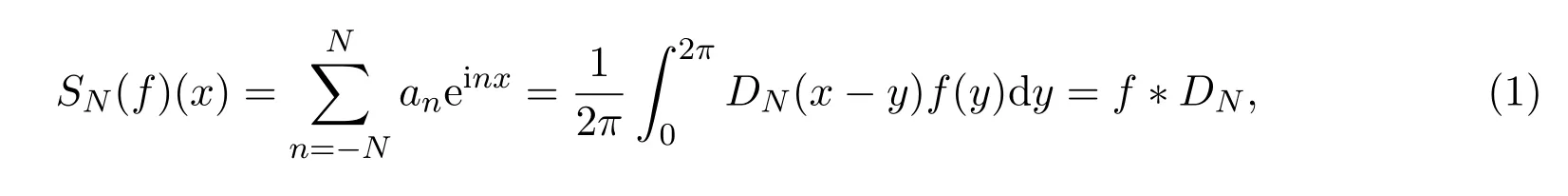
即f（x）的Fourier級數的部分和可視為f（x）與Dirichlet核函數作卷積.

定義2.1給定一族函數｛Kn（x）｝，如果滿足如下三個條件：

注2.1文獻［1］給出了關于優核的非常重要而有用的結論：如果｛Kn（x）｝是一族優核，則若f（x）在點x處連續，必有

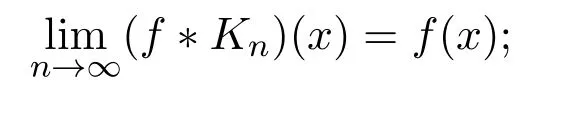
若f（x）處處連續，則極限是一致收斂的.

接下來，以這個結論為出發點，考察f（x）的Fourier級數在不同求和方式下的收斂問題.

3　三類核函數研究

首先考察Dirchlet核函數，有如下結論.

定理 3.1Dirichlet核函數不是優核.

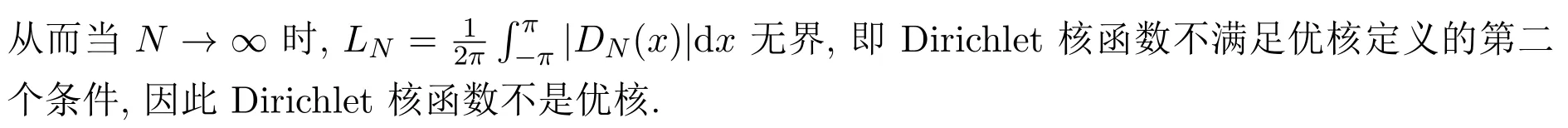
如果函數f（x）只滿足連續性條件，那么其Fourier級數不能保證收斂到f（x），這與定理2.1的結論相符.那么如何去改進呢？文獻［7］指出對級數采用不同的求和方式可能會使發散的級數變得收斂，Abel可和的適用范圍要大于Cesàro可和，而Cesàro可和要比常規可和的適用范圍更廣.受這個結論啟發，本文首先研究將Fourier級數由常規求和改為Cesàro求和會得到什么結論.由（1）式知Sn（f）=f?Dn，現在對Fourier級數取N階Cesàro平均，得

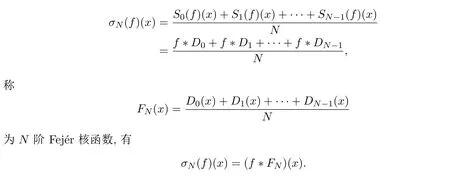
這樣可將Fourier級數在Cesàro求和方式下的收斂性問題轉化為研究函數f（x）與Fejér核函數做卷積的收斂性問題.關于Fejér核函數，有如下結論.

定理 3.2Fejér核函數是優核.

注3.1根據注2.1和定理3.1可知，若函數f（x）在點x處連續，則其Fourier級數的Cesàro和會在點x處收斂到f（x）；如果函數f（x）是處處連續的，則其Fourier級數的Cesàro和會一致收斂到f（x）.

最后研究將Fourier級數求和方式改為適用范圍最廣的Abel求和會有什么結果.

定理 3.3Poisson核函數是優核.

注3.2根據注2.1和定理3.3可得結論：若函數f（x）在點x處連續，則其Fourier級數的Abel和會在點x處收斂到f（x），如果函數f（x）是處處連續的，則其Fourier級數的Abel和會一致收斂到f（x）.

4　結論

函數f（x）的Fourier級數展開可視為f（x）與某個核函數作卷積，對Fourier級數采用不同的求和方式相當于讓f（x）與不同的核函數作卷積.本文首先介紹了優核的概念并指出，一個優核可以讓卷積運算具有好的收斂性.通過這一點可以指出：若對Fourier級數采用常規求和，即讓f（x）與Dirichlet核函數做卷積，并不能保證級數一致收斂到連續函數f（x）；若對Fourier級數采用Cesàro求和或者Abel求和，即讓f（x）與Fejér核函數或Poisson核函數作卷積，則可以保證級數一致收斂到連續函數f（x）.

［1］Stein E M，Shakarchi R.Fourier Analysis，an Introduction［M］.Princeton：Princeton Univ.Press，2011.

［2］Blackledge J M，Digital Image Processing.Mathematical and Computational Methods［M］.Chichester：Horwood Publishing，2005.

［3］Wu Z，Zeng L，Chen G Q，et al.Environmental dispersion in a tidal flow through a depth-dominated wetland［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17：5007-5025.

［4］Zeng L，Chen G Q，Wu Z，et al.Flow distribution and environmental dispersivity in a tidal wetland channel of rectangular cross-section［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17：4192-4209.

［5］Dirichlet G L.Sur la convergence des séries trigonomentriques qui serventà representer une fonction arbitraire entre des limites données［J］.Crelle，Journal für die reine angewandte Mathematik，1829，4：157-169.

［6］Zygmund A.Trigonomentical Series［M］.Cambridge：Cambridge Univ.Press，1959.

［7］張立柱.級數的常規可和，Cesàro可和與Abel可和的幾點討論［J］.純粹數學與應用數學，2013，29（6）：565-571.

［8］陳紀修，於崇華，金路.數學分析［M］.2版.北京：高等教育出版社，2004.

Studies on several kernels in Fourier analysis

Wang Zhizhen
（Mathematics&Science College，Shanghai Normal University，Shanghai200233，China）

Dirichlet kernel，Fejér kernel and Poisson kernel in Fourier analysis are studied in this paper，the concept of good kernel is introduced and we proved that Dirichlet kernel is not a good kernel but Fejér kernel and Poisson kernel are good kernels.

good kernel，Dirichlet kernel，Fejér kernel，Poisson kernel

O173.1

A

1008-5513（2015）03-0238-07

10.3969/j.issn.1008-5513.2015.03.003

2014-08-23.

上海市一級學科建設項目.

王志珍（1974-），博士，副教授，研究方向：魯棒控制，圖像處理，數學分析.

2000 MSC：40C99