Hilbert C?-模中融合框架的新刻畫

相中啟，黃時祥

（上饒師范學院數學與計算機科學學院，江西上饒334001）

Hilbert C?-模中融合框架的新刻畫

相中啟，黃時祥

（上饒師范學院數學與計算機科學學院，江西上饒334001）

觀察到HilbertC?-模中融合框架原定義的不合理性，然后通過權重集的選取將其改進，得到融合框架的新定義并給出其等價形式.特別地，利用算子理論方法得到了HilbertC?-模中融合框架的一個新刻畫.

HilbertC?-模；融合框架；刻畫

1　引言

Hilbert空間中框架的概念由Duffin和Schaeffer［1］于上世紀50年代引入.直到30多年后小波時代開啟的1986年，Daubechies等［2］的突破性研究，才使得框架理論開始被廣泛關注.目前，框架理論已被廣泛應用于信號處理、圖像處理和抽樣理論等方面［35］.更多詳情請參閱文獻［6-10］.

在考慮用局部框架來構造整體框架時，Casazza和Kutyniok［11］定義了Hilbert空間中的融合框架（子空間框架），它是框架概念的推廣.2008年，A.Khosravi和B.Khosravi［12］又將融合框架的概念由Hilbert空間推廣到HilbertC?-模中去，研究了許多與Hilbert空間中融合框架類似的性質.

值得注意的是，雖然HilbertC?-模是Hilbert空間的推廣，但是二者之間還是存在許多的差異.比如，Hilbert空間上關于連續線性泛函的Riesz表示定理并不適用于HilbertC?-模，這蘊含著HilbertC?-模上的某些有界算子沒有伴隨算子；HilbertC?-模中存在不可補的閉子模等.同時應當指出，由于嵌入在HilbertC?-模中的C?-代數的復雜性，以及Hilbert空間中的一些有用的技巧在HilbertC?-模中要么缺失要么未知，從而導致HilbertC?-模中的框架問題要比Hilbert空間復雜許多，框架理論由Hilbert空間到HilbertC?-模的推廣工作并不是平凡的.此外，近年來的研究表明HilbertC?-模理論與小波和框架理論有著多方面的緊密聯系，一方的發展都將對另一方的發展起著積極的促進作用，因此HilbertC?-模中框架的研究工作很有意義.

本文進一步討論HilbertC?-模中融合框架的相關性質.全文主要做了以下兩個方面的工作：一是通過權重集的選取改進了HilbertC?-模中融合框架的原有定義，給出融合框架的新定義并得到了新定義的更便于使用的等價形式；二是從算子理論的角度給出HilbertC?-模中融合框架的一個新刻畫.值得強調的是，該刻畫利用可伴算子的Moore-Penrose逆的相關性質給出了確切的融合框架界.

2　預備知識

本節回顧一些基本定義和性質.首先引入HilbertC?-模的定義.

定義2.1設A是有單位元1A的C?-代數，H是一左A-模，且設A上的線性結構與H上的線性結構是相容的，即

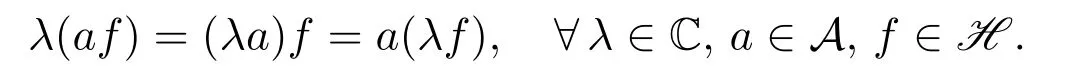
若存在一個映射〈·，·〉：H×H→A滿足：

（1）〈f，f〉≥0，且〈f，f〉=0當且僅當f=0，?f∈H；

（2）〈f，g〉=〈g，f〉?，?f，g∈H；

（3）〈af+g，h〉=a〈f，h〉+〈g，h〉，?a∈A，f，g，h∈H，

則稱｛H，〈·，·〉｝為準HilbertA-模，映射〈·，·〉稱為A-值內積.?f∈H，定義若H關于范數‖·‖完備，則稱｛H，〈·，·〉｝為HilbertA-模，或者A上的HilbertC?-模.

定義2.2設H是C?-代數A上的HilbertC?-模，E?H是一子模.若存在子模F?H使得H=E⊕F，則稱E是可補的.特別地，若E⊕E⊥=H，則稱E是正交可補的.

定義2.3設H和K是C?-代數A上的兩個HilbertC?-模，映射T：H→K稱為可伴的，如果存在映射T?：K→H，使得

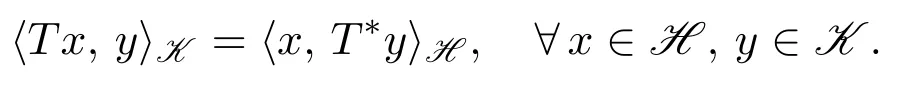
稱T?為T的伴隨算子.

定義2.4設H和K是C?-代數A上的兩個HilbertC?-模，T：H→K是可伴算子，那么可伴算子T?：K→H稱為T的Moore-Penrose逆，如果它滿足：

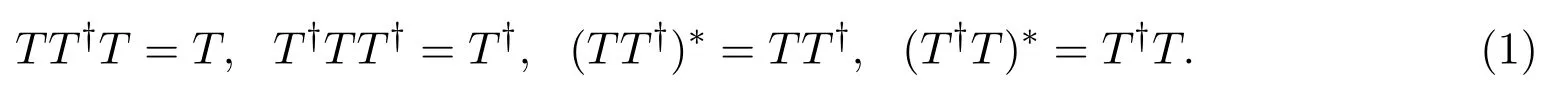
為了證明主要結論，需要下面幾個引理.

引理2.1［13］設H是C?-代數A上的HilbertC?-模，T：H→H是可伴算子，則

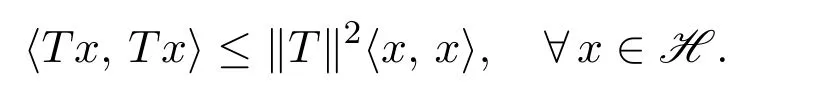
引理2.2［14］設H和K是C?-代數A上的兩個HilbertC?-模，且設T：H→K是可伴算子，則下列條件等價：

（1）T是滿射；

（2）T?關于范數下有界，即存在m＞0使得任意f∈K，‖T?f‖≥m‖f‖；

（3）T?關于內積下有界，即存在m′＞0使得任意f∈K，〈T?f，T?f〉≥m′〈f，f〉.

引理2.3［15］設M和N是C?-代數A上的兩個HilbertC?-模，T：M→N是一線性映射，則下列條件等價：

（1）算子T是有界和A-線性的；

（2）存在常數K≥0使得對所有的x∈M，不等式〈Tx，Tx〉≤K〈x，x〉在A中成立.

引理2.4［16］設H和K是C?-代數A上的兩個HilbertC?-模，T：H→K是可伴算子，則T的Moore-Penrose逆T?存在當且僅當T有閉的值域.

本節最后約定一些記號.本文中，A指有單位元1A的C?-代數，U是HilbertA-模，J是有限或可數指標集.對于j∈J，記πHj表示HilbertC?-模H到其閉子模Hj上的正交投影.

3　HilbertC?-模中融合框架的新定義及其等價形式

HilbertC?-模中融合框架的定義由文獻［12］引入.

定義3.1設｛Pj｝j∈J是U的一列正交可補的閉子模，又設｛υj｝j∈J是A中的一列權重，即每個υj都是正可逆的.如果存在實數0＜C≤D＜∞，使得

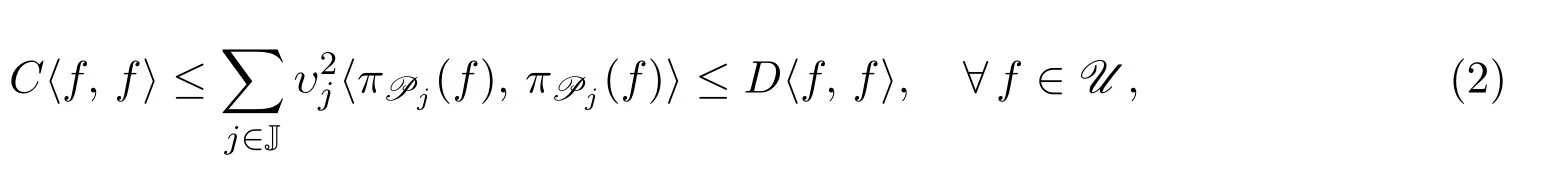
則稱P=｛（Pj，υj）｝j∈J是U的融合框架.

設P=｛（Pj，υj）｝j∈J是U的融合框架，文獻［12］定義其框架算子為：

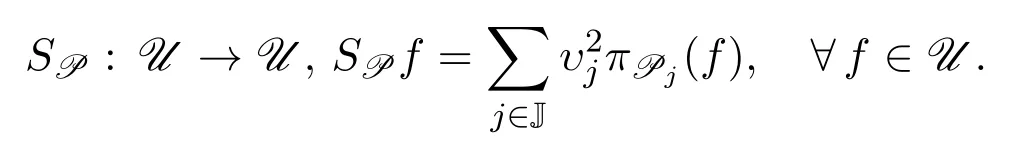
由定義3.1易見SP是可逆的正算子，且SP是自伴的，因為

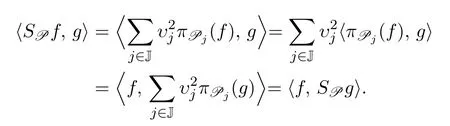
事實上

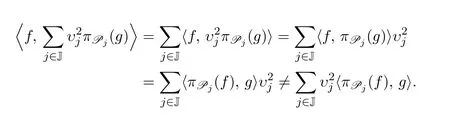
原因在于，作為C?-代數A中的兩個元素，υ2j與〈πPj（f），g〉不一定可以交換次序.注意到，若任意j∈J，υj是正實數，則有

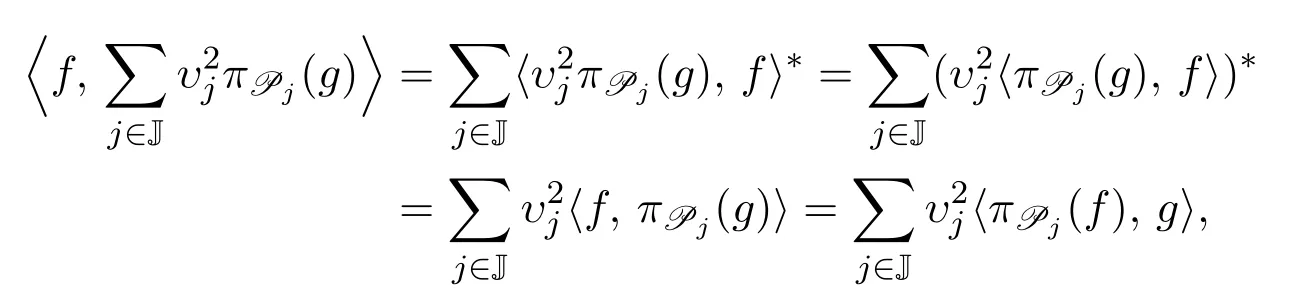
于是可證SP是自伴算子.故可將定義3.1改進為：

定義3.2設｛Pj｝j∈J是U的一列正交可補的閉子模，又設｛υj｝j∈J是R中的一列權重，即每個υj都是正的實數.如果存在實數0＜C≤D＜∞使得

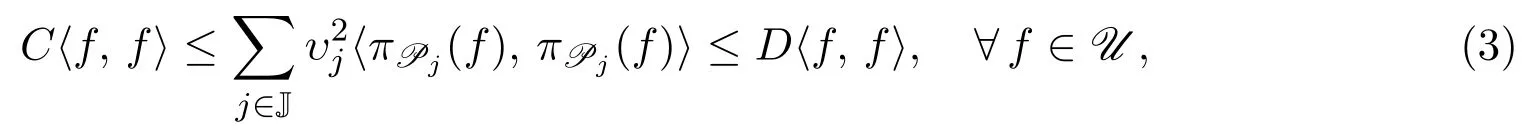
則稱P=｛（Pj，υj）｝j∈J是U的融合框架，C！D稱為融合框架界.如果C=D，則稱P是緊融合框架；如果C=D=1，則稱P是Parseval融合框架.如果（3）式右端的不等式成立，則稱P是Bessel界為D的Bessel融合序列.

設P=｛（Pj，υj）｝j∈J是U的融合框架，則P的框架算子SP定義為：∑

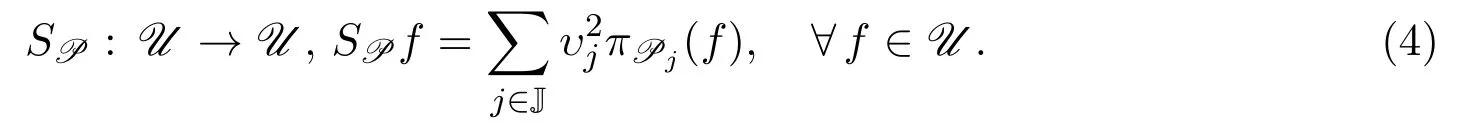
易見SP是可伴的正可逆算子.

下面給出HilbertC?-模中融合框架新定義的更便于使用的等價形式，它的優勢在于對于C?-代數中的兩個正元，比較它們的范數要比比較其自身容易得多.

定理3.1設｛υj｝j∈J是R中的一列權重，｛Pj｝j∈J是U的一列正交可補的閉子模，使得任意f∈U，級數按范數收斂，則P=｛（Pj，υj）｝j∈J是U的融合框架當且僅當存在實數0＜C≤D＜∞，使得

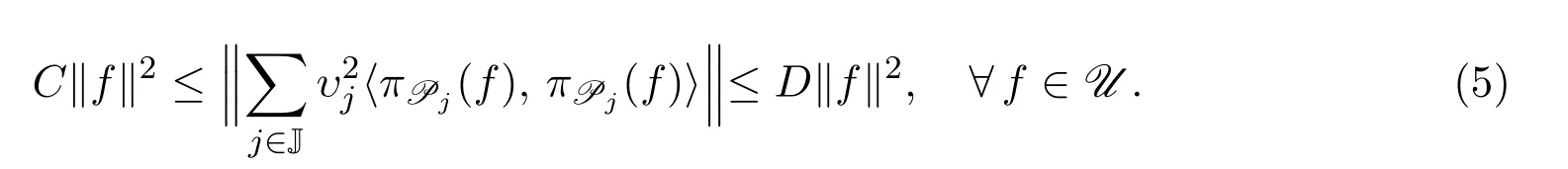
作為定理3.1的一個應用，有如下的Bessel融合序列成為融合框架的等價條件.

定理3.2設P=｛（Pj，υj）｝j∈J是U的Bessel融合序列，則它是融合框架當且僅當對任意的f∈U存在常數M＞0以及序列｛gj，f｝j∈J∈l2（J，U），使得

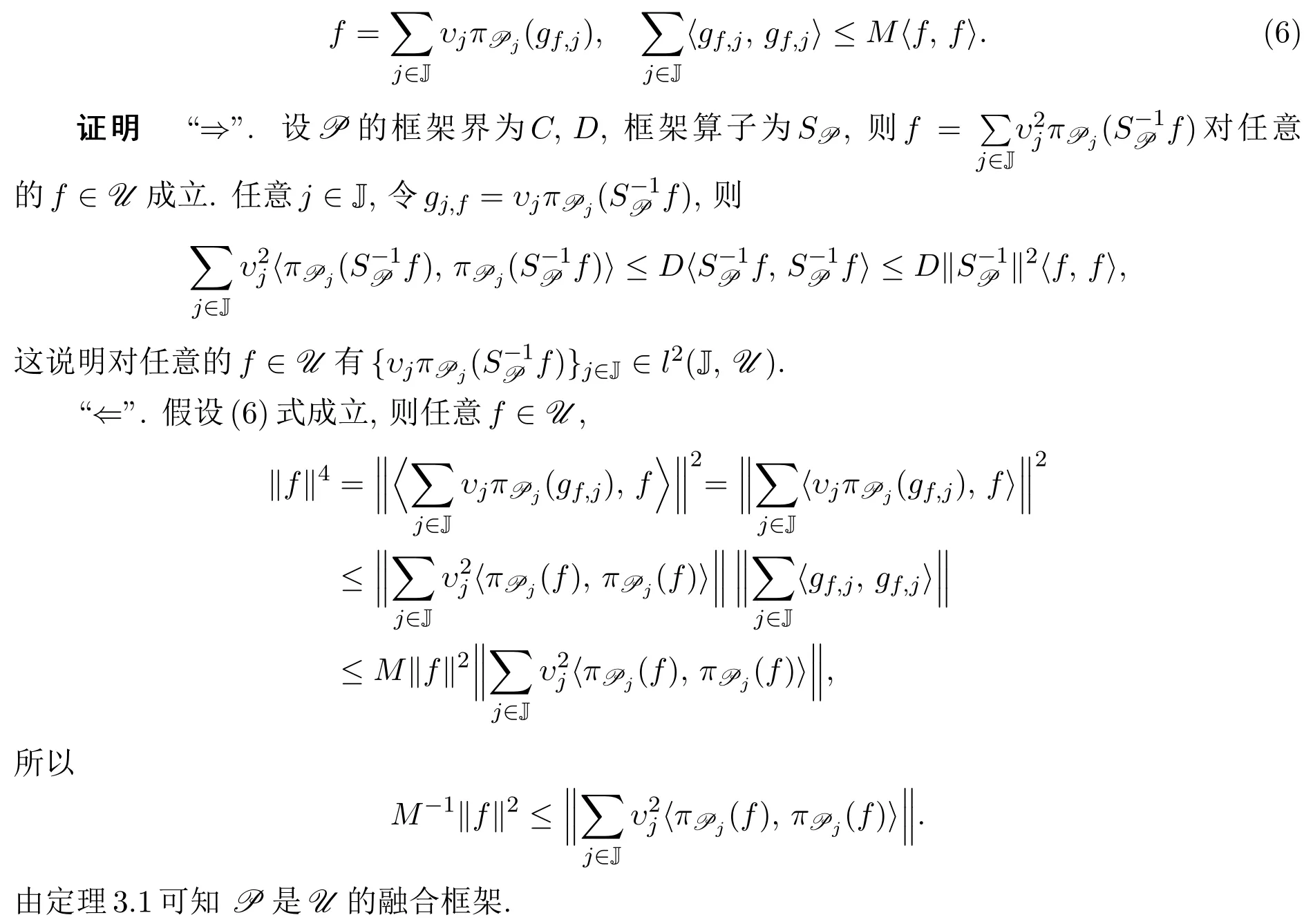
4　HilbertC?-模中融合框架的新刻畫

本節從算子理論的角度給出HilbertC?-模中融合框架的一個新刻畫.

定理4.1設｛υj｝j∈J是R中的一列權重，｛Pj｝j∈J是U的一列正交可補的閉子模，則P=｛（Pj，υj）｝j∈J是U的融合框架當且僅當算子

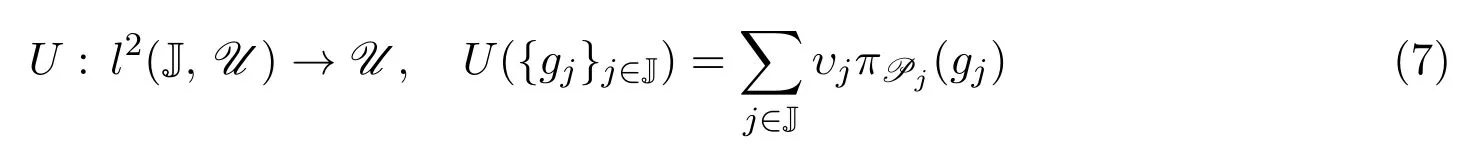
是已定義的有界滿射算子.此時框架界為‖U?‖-2，‖U‖2，其中U?是U的Moore-Penrose逆.

推論4.1設｛υj｝j∈J是R中的一列權重，｛Pj｝j∈J是U的一列正交可補的閉子模，則P=｛（Pj，υj）｝j∈J是U的Bessel界為D的Bessel融合序列當且僅當（7）式中的算子U是已定義的有界算子且

注4.1（1）如果J是有限集，則｛υj｝j∈J∈l∞（J），于是可知U是已定義的有界算子.

（2）由定理4.1的證明過程可知，如果U是已定義的有界算子，則它是可伴的且其伴隨算子由下式給出：

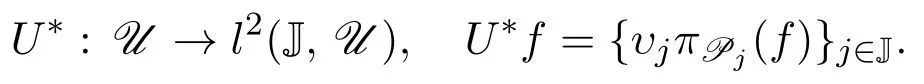
（3）假設J不是有限集，U是已定義的.若U有界，則｛υj｝j∈J∈l∞（J）.若則對任意k∈N存在υjk＞k.任意選取fjk∈Pjk滿足‖fjk‖=1，則有

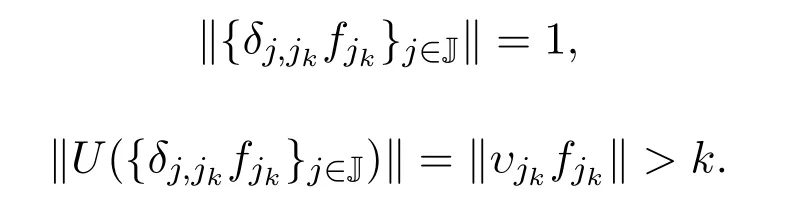
因此U不是有界算子.

［1］Duffin R J，Schaeffer A C.A class of nonharmonic Fourier seriers［J］.Trans.Amer.Math.Soc.，1952，72（2）：341-366.

［2］Daubechies I.Ten Lectures on Wavelets［M］.Philadelphia：SIAM，1992.

［3］Feichtinger H G，Strohmer T.Gabor Analysis and Algorithms：Theory and Applications［M］.Boston：Birkh?user，1998.

［4］Feichtinger H G，Strohmer T.Advances in Gabor Analysis［M］.Boston：Birkh?user，2003.

［5］Casazza P G.Modern tools for Weyl-Heisenberg frame theory［J］.Adv.Imag.Elect.Phys.，2001，115（1）：1-127.

［6］Christensen O.An Introduction to Frames and Riesz Bases［M］.Boston：Birkh?user，2002.

［7］唐青松，張祥德，陸小軍，等.非均勻Gabor框架的穩定性［J］.純粹數學與應用數學，2009，25（4）：828-832.

［8］李嵐.算子框架的穩定性［J］.純粹數學與應用數學，2008，24（1）：375-378.

［9］相中啟，賈琛琛.Christensen的改進結果在研究框架擾動中的應用［J］.蘭州大學學報：自然科學版，2012，48（4）：115-118.

［10］相中啟，簡輝華.Hilbert空間中連續框架擾動的新結果［J］.蘭州大學學報：自然科學版，2013，49（3）：405-408.

［11］Casazza P G，Kutyniok G.Frames of subspaces［J］.Contemp.Math.，2004，345：87-113.

［12］Khosravi A，Khosravi B.Fusion frames and g-frames in Hilbert C?-modules［J］.Int.J.Wavelets Multiresolut.Inf.Process，2008，6（3）：433-466.

［13］Lance E C.Hilbert C?-modules：A Toolkit for Operator Algebraist［M］.Cambridge：Cambridge University Press，1995.

［14］Aramba?i? L.On frames for countably generated Hilbert C?-modules［J］.Proc.Amer.Math.Soc.，2007，135（2）：469-478.

［15］Paschke W L.Inner product modules over B?-algebras［J］.Trans.Amer.Math.Soc.，1973，182：443-468.

［16］Xu Q X，Sheng L J.Positive semi-definite matrices of adjointable operators on Hilbert C?-modules［J］.Linear Algebra Appl.，2008，428（4）：992-1000.

New characterization of fusion frames in Hilbert C?-modules

Xiang Zhongqi，Huang Shixiang
（College of Mathematics and Computer Science，Shangrao Normal University，Shangrao334001，China）

An observation shows that the original definition of fusion frames in Hilbert C?-modules is unreasonable and then，it is improved by a replacement of the associated weight set.An equivalent form of the new definition of fusion frames in Hilbert C?-modules is also given and，especially，a new characterization of fusion frames in Hilbert C?-modules is obtained by the method of operator theory.

Hilbert C?-module，fusion frame，characterization

O174.6

A

1008-5513（2015）05-0456-08

10.3969/j.issn.1008-5513.2015.05.003

2014-12-28.

國家自然科學基金（11271148）.

相中啟（1979-），博士，講師，研究方向：分形理論與小波分析.

2010 MSC:46L99，42C15