基于紅外檢測乳腺腫瘤的多參數反演研究*

黃鑒，盧玫，李博漢，張濤

(上海理工大學，能源與動力工程學院，上海 200093)

1 引 言

乳腺癌為女性中最常見的惡性腫瘤，其發病率自上世紀70年代末起一直呈上升趨勢，已成為當前社會的重大公共衛生問題。早期發現、早期診斷是提高療效、降低乳腺癌死亡率的關鍵。目前診斷的方法主要有X射線、CT檢測、MRI檢測等方法，這些方法或者昂貴，或者會對人體有一定的傷害。隨著紅外熱像儀測量精度的不斷提高，使得熱像儀越來越多的被用到乳腺腫瘤診斷中。

通過紅外熱像儀檢測獲得的紅外熱像圖來診斷乳腺腫瘤[1]的方法主要是比對病變乳腺體表溫度與正常乳腺體表溫度，這種診斷方法僅是一種定性分析。其實，乳腺體表溫度不僅與腫瘤的性質有關，也與腫瘤的大小、位置、個體乳腺組織的導熱系數等諸多因素有關。國內外學者在紅外檢測乳腺腫瘤方面已做了一些研究，Gonz′alez[2]研究了不同熱像儀測量精度條件下，各種大小腫瘤能被檢測到的最大深度。Mital等[3]在二維計算模型下，根據單一的目標函數對乳腺腫瘤的位置、大小及代謝產熱進行反演計算，并獲得較高精度的解。Bezerra[4]等對乳腺腫瘤的導熱系數及內部的血液灌注率進行反演計算，并實驗研究了熱像儀與人體之間距離對反演精度的影響。研究者在求解此類反問題時用到的優化方法主要有序列二次規劃法[4]，遺傳算法[5]，神經網絡法[6]，模式搜索法[7]等。在求解反問題時，不論采用哪種優化算法，都需利用測點溫度信息建立一個目標函數，而單一目標函數在反演多個參數時，對各個參數的優化調整存在一定的盲目性。

本研究以紅外熱像儀檢測乳腺腫瘤為應用背景，通過紅外熱像儀測得的體表溫度，建立與反演參數相關的多目標函數，并對所采用的粒子群優化算法中的更新方式進行了相應的改進，以提高多參數反演的準確度和計算速度。

2 物理模型和數學描述

2.1 物理模型

本研究所討論的物理問題原型是根據紅外檢測乳腺腫瘤所得到的體表溫度定量分析腫瘤的位置、腫瘤代謝熱強度和和乳腺組織的導熱系數。這一問題可以抽象為一個含有內熱源的多參數導熱反問題。首先將檢測對象簡化為如圖1所示的半球體，直徑d=0.144 m；腫瘤及腫瘤代謝熱抽象為半徑r=0.01 m的球體熱源；底面Γb為腔體內平面，半球面Γt為紅外檢測乳腺體表面。人體表面的散熱包括體表與周圍環境的對流換熱、輻射換熱和汗液的蒸發，檢測時人體靜坐，因此忽略汗液蒸發。根據測量所得熱像圖，選用若干觀測點溫度，反演熱源位置、熱源強度及導熱系數。

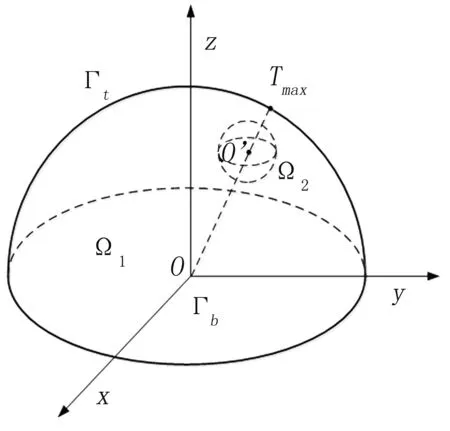
圖1 腫瘤檢測抽象模型Fig 1 Abstract model for tumor detection

2.2 數學描述

為便于建立數學模型和計算，坐標系設置見圖1。半球底面置于坐標系xoy平面，紅外熱像圖中表面溫度最高點置于坐標系yoz平面。由于半球體內部物性參數均勻，半球表面熱邊界條件相同，所以熱源中心也在yoz平面，且半球體溫度場對稱于yoz平面。描述上述物理問題的微分方程采用如式(1)所示的生物體傳熱方程—PENNES[8]方程，對應的定解條件如式(2)～(4)所示。

λ2T+wbiρbθb(Tb-T)+Qmi=0

(1)

∈Ω=Ω1+Ω2
T=T0∈Γb

(2)

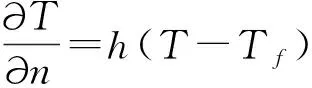
(3)

T=Tm，,jj=1，2，3……n

(4)

式中，T為溫度，℃；Tb為血液溫度，℃；λ為導熱系數，W/m·℃；wbi為血液灌注率，s-1；ρb為血液密度，kg/m3；cb為血液比熱容，J/kg·℃；Qmi為組織的代謝產熱，W/m3；下標i=1，2，分別對應正常乳腺組織區域Ω1及腫瘤區域Ω2；T0為半球底面溫度，℃；Tf為環境溫度，℃；h為考慮對流換熱和輻射換熱的總換熱系數，W/m2·℃；Tm,j為邊界觀測點測量溫度，℃；n為測點數。

3 多參數導熱反問題的求解

導熱反問題求解的一般流程為：首先對反演參數隨機預測一個值，根據預測值求解式(1)～(3)所描述的導熱正問題，得到求解區域的溫度場，然后跟據觀測點的計算溫度值Tc,j和式(4)給出的測量溫度值計算由式(5)定義的目標函數值：

(5)

若目標函數F值滿足收斂條件，則反演結束；若不滿足，則通過優化算法調整反演參數值，重新代入式(1)～(3)計算，直至目標函數F滿足收斂條件。

3.1 輔助目標函數

在多參數反演過程中，僅以式(5)所示單一目標函數作為多個參數調整的依據存在盲目性。不同的物理參數對邊界溫度存在不同的影響，鑒于這一特點，考慮在式(5)所示目標函數基礎上，增加與被反演參數相應的輔助目標函數，用于多參數反問題求解過程中參數的調整、優化。針對本研究的導熱反問題，則分別研究熱源位置、導熱系數等參數對表面溫度影響的規律，然后在此基礎上建立相應的熱源位置目標函數和導熱系數目標函數。

(1) 熱源位置目標函數

李博漢[9]等在反演熱源位置的導熱反問題中采用了相關度作為目標函數，其表達式為：

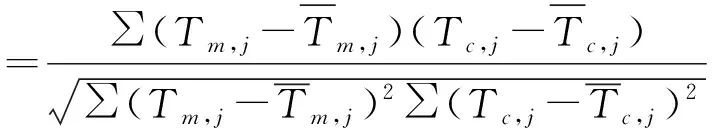
(6)

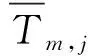
在同時反演多個參數的情況下，如果相關度受熱源強度、導熱系數影響不大，則仍可沿用此相關度。為此計算了熱源位置、導熱系數和代謝熱強度等反演參數分別偏離真實值時的相關度，結果見表1。可以看出，相關度受腫瘤位置影響較大：預測位置與真實位置偏差越大，相關度就越小；而相關度受導熱系數及熱源強度的影響較小。因此，式(6)定義的相關度也適合應用在多參數導熱反問題中，作為搜索熱源位置的輔助目標函數。

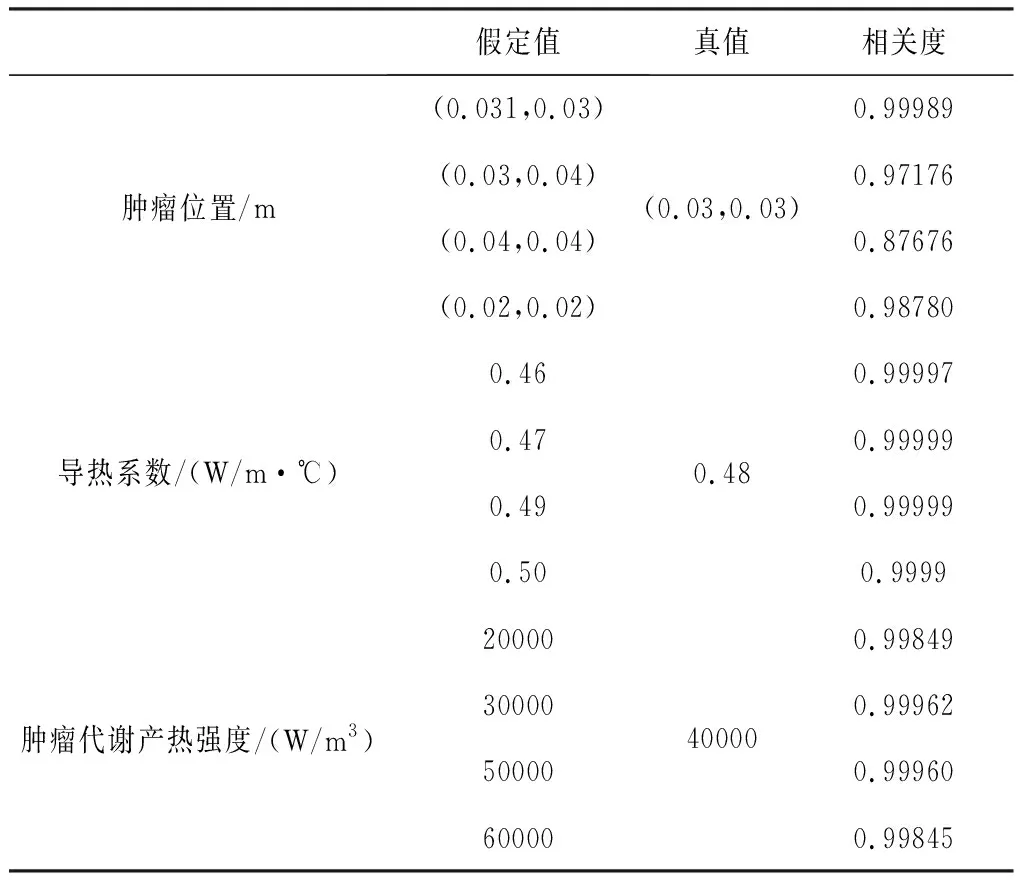
表1 各參數對相關度的影響

(2)導熱系數目標函數

導熱系數反應了物體熱傳導的能力，物體置于同樣的環境中，較強的熱傳導能力使內部的熱量容易向外傳遞，邊界散熱的熱流密度增大，邊界溫度增加，反之邊界溫度將降低。為分析導熱系數與熱源強度、熱源位置對邊界溫度的相對影響，計算了表2所示工況的溫度場，并將邊界上觀測點溫度值繪制成圖2所示曲線。

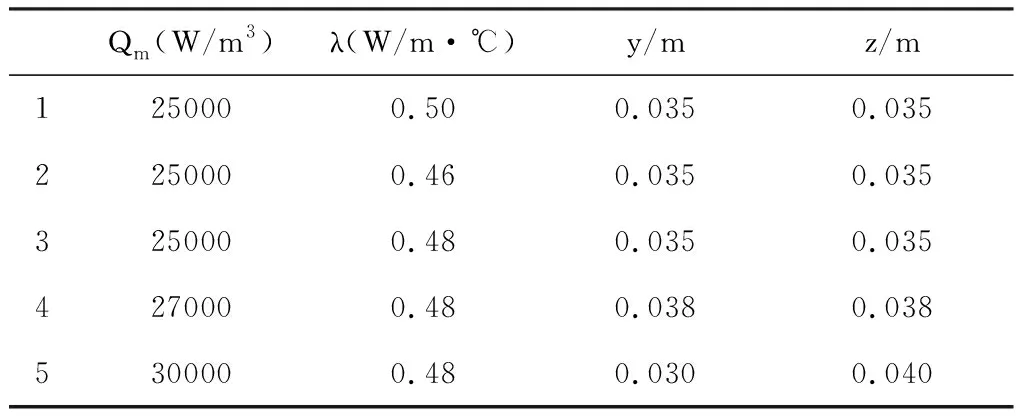
表2 熱源參數及導熱系數取值

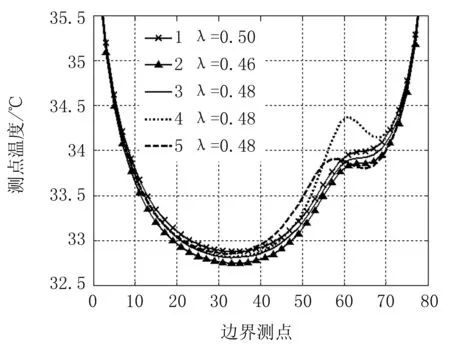
圖2不同導熱系數對應邊界測點溫度示意圖

Fig2Testpointstemperaturefordifferentthermalconductivity

圖2曲線1、2、3分別對應表2計算工況1、2、3。可以看出，隨著導熱系數增大，邊界上各觀測點溫度值均相應增大。圖2曲線3、4、5分別對應表2計算工況3、4、5，即導熱系數不變、熱源位置和熱源強度變化的3個計算工況。由曲線3、4、5可以看出，熱源強度、熱源位置的變化對靠近熱源位置的邊界溫度影響較大，而在距離熱源位置較遠的邊界區域，如測點10～20，三個工況對應的溫度曲線基本重合，這說明該區域溫度受熱源位置、熱源強度影響很小。因此，當計算得到的導熱系數趨于真值時，該區域觀測點的計算溫度應趨于測量溫度值。根據這一特點可以建立式(7)所示的眾數為反演導熱系數的輔助目標函數：

M=mode(Tm,1-Tc,1，Tm,2-Tc,2，…Tm,n-Tc,n)

(7)

所有邊界測點溫度計算值與測量值之差的絕對值中出現頻率最高的數即為眾數，眾數越接近0，則說明反演參數中的導熱系數越接近真值。

3.2 粒子群算法更新方式改進

粒子群算法PSO(particle swarm optimization，PSO)[10]是Kennedy和Eberhart提出的一種基于群體智能的全局隨機搜索算法。粒子群算法中，每個粒子在求解空間中的位置代表了優化過程中的一組預測值，并以各自的速度在求解空間內搜索，其基本位置和速度更新方程為:

xi(k+1)=xi(k)+vi(k+1)

(8)

vi(k+1)=ωvi(k)+c1r1[xpbesti(k)-xi(k)]+c2r2[xgbest(k)-xi(k)]

(9)

式中，k為迭代步計數；xi為粒子i在求解空間中位置矢量，x=(x1,x2,…xN)，N為反演參數數目，即求解空間維數；i=1,2,3,…,s，s為粒子總數；vi為粒子i飛行速度矢量，v=(v1,v2,…vN)；ω為慣性權重；c1為認知系數；c2為社會系數；r1、r2為[0,1]均勻分布的隨機數；xpbesti為粒子i所經過的所有位置中目標函數F值最小的位置；xgbest為全部粒子所經過的所有位置中目標函數F值最小的位置。

由式(8)～(9)所描述的更新方程可知，僅有一個目標函數時，粒子搜索下一個空間位置的三個飛行速度分量，由目標函數F控制。而本研究提出了與反演參數相關的多目標函數后，則可以根據輔助目標函數對飛行速度分量進行調整。因此，需要對上述更新方程做出相應的改進(改進粒子群算法—modified particle swarm optimization，MPSO)。

針對熱源位置和導熱系數反演參數，計算過程中分別記錄下所有粒子經過的相似度最高的位置xgpbest1、xgpbest2和眾數最小的位置xgpbest3，這些位置中分別具有相對最優的熱源位置和導熱系數。飛行速度分量更新方程為：

vij(k+1)=ωvij(k)+c1r1[xpbestij(k)-xij(k)]+c2r2[xgbest j(k)-xij(k)]+c3r3[xgpbest j(k)-xij(k)]

(10)

式(10)中，j=(1,2,3)；c3為多目標社會系數；r3為均勻分布隨機數。與式(9)相比，式(10)對速度的調整增加了由輔助目標函數確定的第四項。

對于熱源位置參數，定義xgpbestj，j=1,2的更新方程為：

(11)

對于導熱系數，定義xgpbestj,j=3的更新方程為：

(12)

4 數值計算結果及分析

計算時，設半球底面溫度Tc=37℃，半球體表面總對流換熱系數h=5W/(m2·℃)，環境溫度Tf=22℃。 PENNES方程中各參數設置見表3。

表3 PENNES方程物性參數

表4粒子群算法系數取值及參數搜索范圍

Table4ValuesofcoefficientsinMPSO,PSOandestimatedparameters’searchsope

粒子數s10最大迭代次數kmax300慣性權重ω0.8-kkmax×0.8 認知系數c12.0社會系數c2kkmax×0.2 多目標社會系數c30.2-kkmax×0.2 熱源強度搜索范圍700≤Qm≤70000導熱系數搜索范圍0.46≤λ≤0.500.22≤y2+z2≤0.58熱源位置搜索范圍θ=arctan(zy)根據熱像圖上溫度最高測點及相鄰兩個測點確定

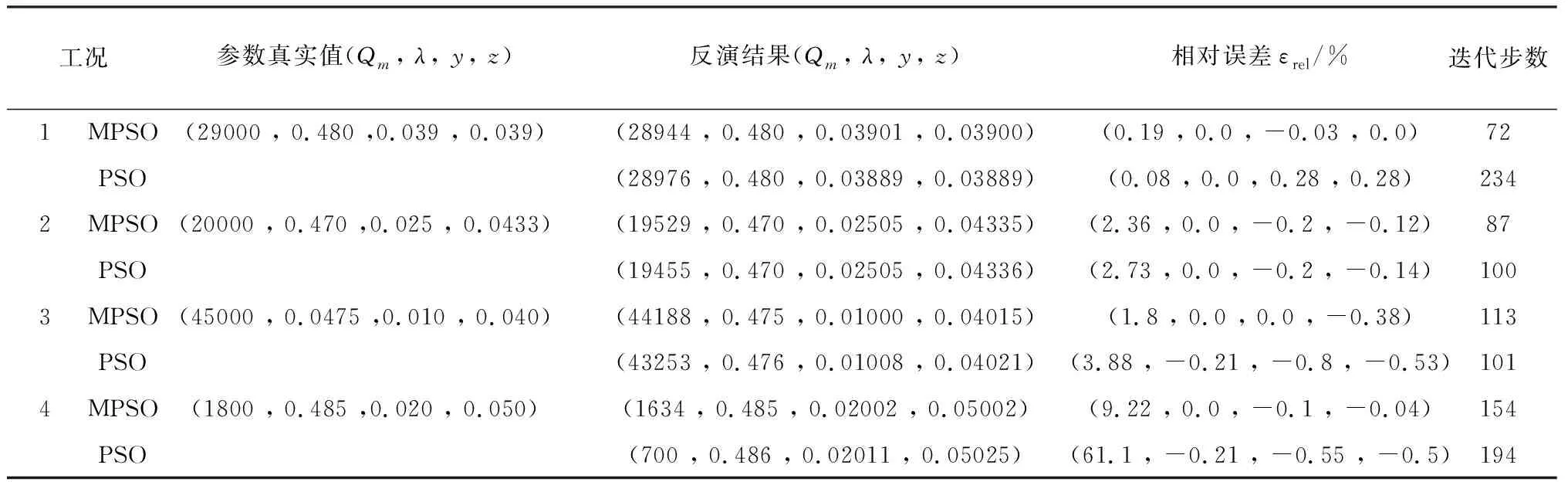
分別采用MPSO和PSO兩種方法對不同工況進行反演計算，其計算結果列于表5。

表5所列結果顯示，三個反演參數中導熱系數及熱源位置的相對誤差較小, 均在1%以內，而熱源強度的相對誤差較大。圖3所示為各工況中反演得到的熱源強度的誤差絕對值，圖4為對應工況的測點溫度分布曲線。對照圖3、圖4可以發現，體表溫度變化越大，計算結果誤差就越小。相同病變情況下，MPSO反演得到的結果，其相對誤差普遍小于PSO，而且在體表溫度變化微弱的情況下，更能顯示出MPSO的優勢。通過四組不同算式的計算，MPSO達到收斂條件的迭代步數約為100，相較PSO約為150的平均迭代步數，反演所需時間縮短33%。

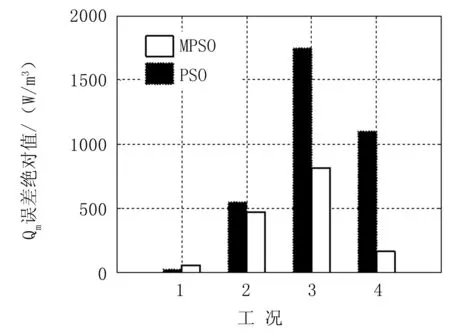
圖3 Qm誤差絕對值

工況參數真實值(Qm, λ, y, z)反演結果(Qm, λ, y, z)相對誤差εrel/%迭代步數1MPSO(29000 , 0.480 ,0.039 , 0.039)(28944 , 0.480 , 0.03901 , 0.03900)(0.19 , 0.0 , -0.03 , 0.0)72PSO(28976 , 0.480 , 0.03889 , 0.03889)(0.08 , 0.0 , 0.28 , 0.28)2342MPSO(20000 , 0.470 ,0.025 , 0.0433)(19529 , 0.470 , 0.02505 , 0.04335)(2.36 , 0.0 , -0.2 , -0.12)87PSO(19455 , 0.470 , 0.02505 , 0.04336)(2.73 , 0.0 , -0.2 , -0.14)1003MPSO(45000 , 0.0475 ,0.010 , 0.040)(44188 , 0.475 , 0.01000 , 0.04015)(1.8 , 0.0 , 0.0 , -0.38)113PSO(43253 , 0.476 , 0.01008 , 0.04021)(3.88 , -0.21 , -0.8 , -0.53)1014MPSO(1800 , 0.485 ,0.020 , 0.050)(1634 , 0.485 , 0.02002 , 0.05002)(9.22 , 0.0 , -0.1 , -0.04)154PSO(700 , 0.486 , 0.02011 , 0.05025)(61.1 , -0.21 , -0.55 , -0.5)194

圖5所示為分別采用PSO和MPSO求解算例4時各反演參數時最優解(xgbest)的收斂曲線，在圖5(a)、5(b)中一個較為明顯的特征是， PSO搜索得到最優熱源位置收斂曲線變化緩和，下一個迭代步獲得的最優解近似于上一步。而MPSO有較多的鋸齒型波動，下一步獲得的最優解與上一步相比更似一個突變。這是由于PSO在位置更新時僅受單一目標函數控制，而MPSO在搜索熱源位置的過程中，位置更新受到兩個目標函數的影響，并且這兩個目標函數所確定的熱源位置最優解通常是不一致的，這勢必會增大粒子的搜索范圍，使其能不拘泥于原來的最優解，因此，MPSO中粒子有著更強的搜索能力，并最終得到更接近真值(y=0.02,z=0.05)的解；圖5(c)顯示的最優導熱系數收斂曲線所反映的情況與熱源位置收斂曲線近似，MPSO在搜索導熱系數時同樣受輔助目標函數影響，最終的反演結果也是MPSO優于PSO。而從圖5(d)曲線中可以看出PSO在搜索熱源強度時陷入了搜索范圍的下界限，并在之后的搜索過程中一直困于局部最優解。MPSO搜索結果也一度到達下界限，但隨后便跳出局部最優，并最終獲得與真值接近的解，這說明輔助目標函數雖沒有直接影響粒子在搜索熱源強度時的更新方式，但間接的對搜索過程帶來了積極的影響。圖6為目標函數F收斂曲線，其結果表明PSO在經過30次左右的迭代步后，目標函數值下降非常緩慢，說明求解已經陷入了局部最優。而MPSO在30次迭代步之后的搜索過程中，目標函數值依然不斷下降。

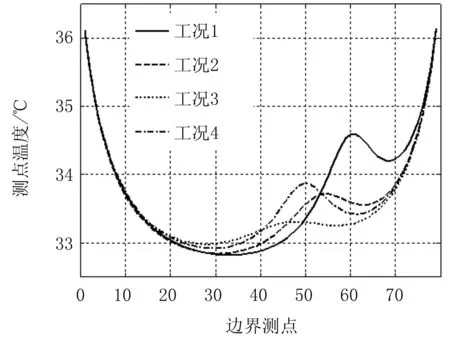
圖4各工況測點溫度分布圖

Fig4Thedistributionoftestpointstemperatureinfourcases

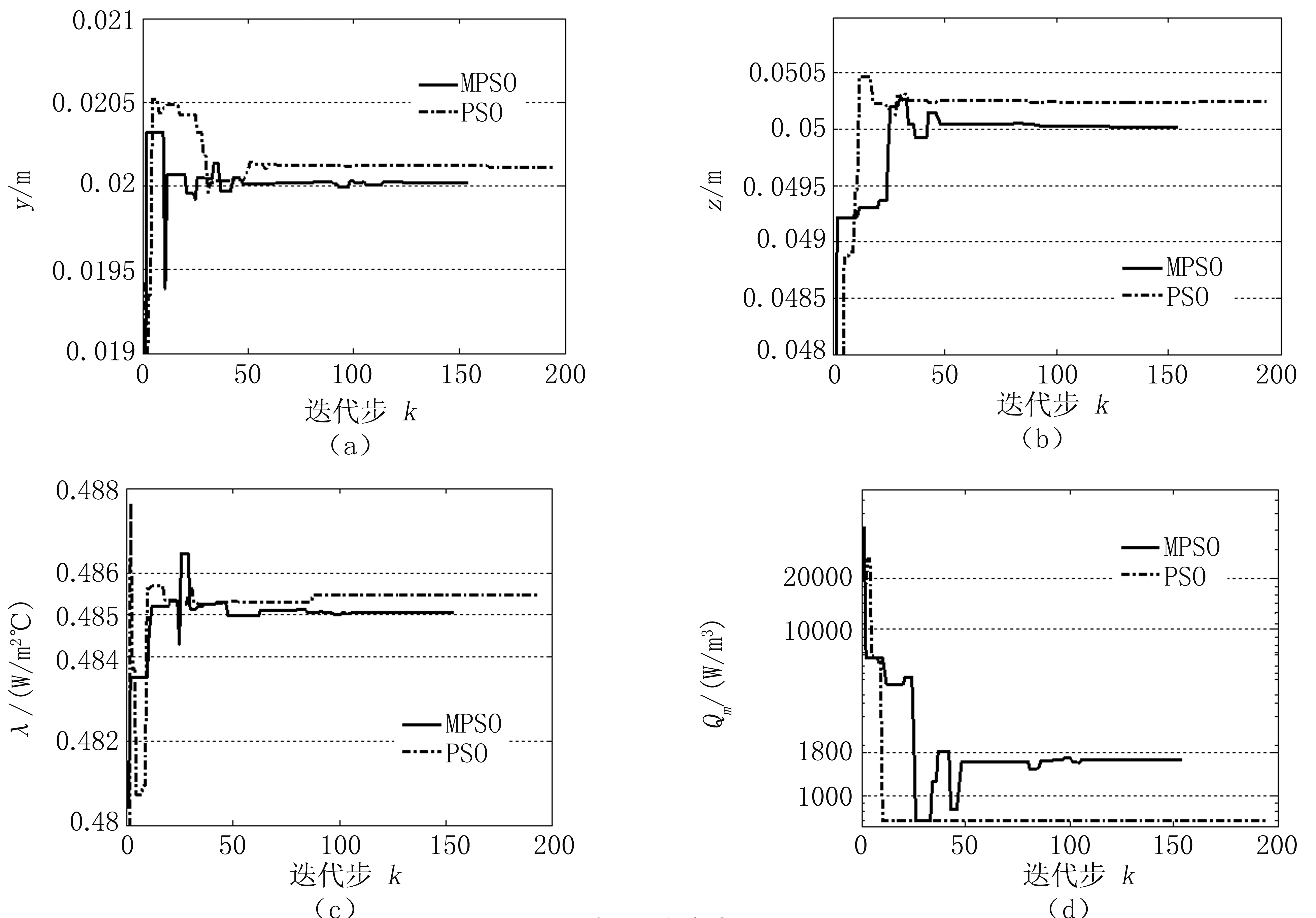
圖5各反演參數收斂曲線
(a)熱源位置y坐標收斂曲線； (b)熱源位置z坐標收斂曲線；
(c)導熱系數λ收斂曲線； (d)熱源強度Qm收斂曲線；
Fig5Convergenceplotofmultivariables

(a) convergence plot of y; (b) convergence plot of z; (c) convergence plot of λ; (d) convergence plot of Qm

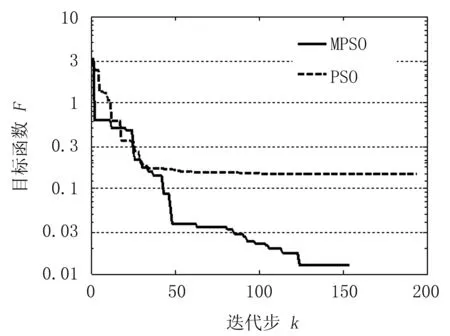
圖6 目標函數F收斂曲線Fig 6 Convergence plot of fitness fuction F

粒子群算法是一種基于概率的算法，反演求解過程中具有隨機性，引入輔助目標函數，增大了粒子在位置更新過程中遇到全局最優解的概率。相似度目標函數及眾數目標函數所確定的最優熱源位置，及最優導熱系數以xgpbest項的形式參與到粒子的更新過程中，使得粒子群反演參數中的熱源位置項及導熱系數項往xgpbest靠攏，從而增大得到全局最優解的概率。

5 結論

本研究采用粒子群算法，根據紅外熱像圖上觀測點的溫度，可準確反演出內部腫瘤未知參數。同時根據熱源位置、導熱系數對邊界溫度的不同影響，建立相關度及眾數作輔助目標函數的多目標粒子群算法，通過對不同的工況的數值模擬結果表明：與PSO相比，MPSO計算收斂速度快，獲得的解更精確；在搜索過程中，最優解更新頻次高，不易陷入局部最優；在觀測點溫度差異小的工況下，MPSO的優勢更為明顯，提高了反演的準確性。