數形結合思想的教學探尋與思考

凌伯軍

【關鍵詞】數形結合 數學思想

教學方法 思考

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2015）09A-

0037-02

“數”與“形”是數學的兩塊根基，在數學發展進程中，它們常常結合在一起，在內容上互相聯系，在方法上互相交織，在思想上互相滲透。重視“數”與“形”的和諧融合，可使數學問題化難為易，化繁為簡，幫助學生更好地學習數學，是每一個數學教師理應重點思考的問題。

一、“數”“形”邂逅的策略與價值

（一）在混沌處“邂逅”，讓知識清晰明了

其實，有些數學問題不僅僅是簡單的以“數”變“形”，或以“形”變“數”，而是“形”與“數”的互相轉換，有時是“形”的直觀變為“數”的嚴密，有時是“數”的嚴密聯系到“形”的直觀。學生在解決問題時，往往需要認真分析其內在的“形”“數”之間的聯系，實現有效的互相轉換。常用的方法有看“形”想“數”和見“數”思“形”兩種。

為了加深學生對加法和乘法的理解，筆者在教學乘法的相關知識后設計了一組練習：13+4和13×4，讓學生用手中的學具來擺一擺、說一說，這兩個算式表示什么意思。

生1：13+4，先擺13根小棒，再擺4根小棒，然后把3根小棒和4根小棒先合在一起，是7根，最后和一捆合一起就是17根。

生2：13×4，先擺13根小棒，又擺13根小棒，再擺13根，還要擺13根，表示的是4個13根小棒相加，所以是52根，和上面的13+4是不同的。

師：其他同學聽明白了嗎？第一個表示13根和4根合起來，而13×4則表示4個13根合起來。

這樣，通過學生自己擺小棒、說算理，進行了清晰地對比，讓學生從加法和乘法各自意義的角度深刻地理解了為什么乘法中的一位數要與多位數的每一個數位上的數字相乘，而加法只要相同數位的數字相加。

（二）在復雜處“邂逅”，讓問題簡單易做

數學是關于現實世界的空間形式和數量關系的學科，學生要深刻理解這些復雜的數量關系存在的困難，這時就需要教師深入研究，找準數與形的契合點，將數與形巧妙地結合起來，引導學生畫一畫，借助直觀圖形，化復雜為簡單，引發聯想，促進形象思維和邏輯思維的融合。

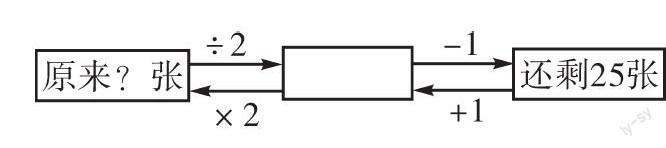
如，蘇教版五年級下冊《解決問題的策略》單元第89頁練一練：小軍收集了一些畫片，他拿出畫片的一半還多1張送給小明，自己還剩25張。小軍原來有多少張畫片？很多學生都是這樣解決的：25×2=50（張），50+1=51（張）。這樣的解法明顯是倒推的順序錯了，如果讓學生把小軍的畫片變化的過程畫出來（如下圖），倒推就變得相對簡單了。

由于畫出了小軍畫片的變化圖，學生很清楚地看出了畫片變化的過程，為倒過來推想提供了有效的幫助，學生很快尋找到了解決問題的辦法：先把多送的1張拿回來，25+1=26（張），再擴大2倍算出原來的張數，26×2=52（張）。

（三）在抽象處“邂逅”，讓思維自然生成

在教學抽象概念時，如果能將抽象概念與形象圖形聯系起來，把“數”和“形”結合起來，就可以豐富學生的感性材料，為建構與理解數學概念奠定堅實的基礎。

例如，在教學蘇教版四年級下冊《素數和合數》時，筆者改變了教材的思路，而是首先從哥德巴赫猜想引入，讓學生通過閱讀哥德巴赫猜想，學生發現3、5、7是素數，但不知道什么是素數。然后筆者分別用3個、5個、7個小正方形來表示3、5、7這三個數，引導學生觀察拼成的長方形，理解3、5、7這三個數有什么共同點？

通過分別出示3個正方形、5個正方形和7個正方形的演示，幫助學生建立3、5、7這三個數和形的聯系；通過分別將3個正方形、5個正方形和7個正方形拼成一個長方形的演示，幫助學生進一步深層次地去發掘3、5、7這三個數的聯系（只能拼成一種長方形），進而找到3、5、7這三個數同為素數的聯結點。形象直觀的圖形演示，有助于“數”的概念本質把握。

（四）在總結處”邂逅”，讓學習聯為一體

數學知識之間是有機聯系的，具有嚴密性和系統性等特點。教師可以引導學生將已有知識，根據一定的統一標準分類，使之更加條理化和系統化，使所學的知識形成連續的數學知識結構。比如，在教學蘇教版五年級數學上冊《認識小數》后，筆者設計了這樣的總結：

師：今天我們發現，當不能用整數表示時，就把1平均分成10份，每一份就是十分之一，也就是今天我們認識的0.1，這也是一個計數單位；如果這個計數單位還是太大，怎么辦？再把十分之一平均分成10份，每一份是百分之一。還太大呢？再繼續平均分成10份，就這樣每次把計數單位平均分成10份，其中的一份就產生了更小的計數單位。

師：你們看，這樣小數家族的整數部分就越來越壯大了，向左計數單位越來越大，向右計數單位越來越小。它們還是以小數點為分界點。

有了這樣數和形的緊密結合，更能加深學生對小數的理解，并且對每個計數單位的大小有了直觀認識，這樣，讓學生看“形”思“數”、見“數”想“形”，從本質上對小數有了深刻的認識。

二、“數”“形”邂逅的思考與建議

數形結合既能體現數的嚴謹，又能展現形的直觀，是一種重要的數學思想和數學方法。小學生抽象思維能力較差，數形“嫁接”是化抽象為直觀的一種很有效的方法。“數形邂逅”也要講求契機，那教學中我們需要注意什么呢？

（一）當學生理解困難時

荷蘭著名數學教育家弗賴登塔爾提出：學生的學習活動，與其說是學習數學，不如說是學習“數學化”。低年級學生對于題目中的有用信息進行輸入、處理是教學難點，特別是部分接受能力、理解能力較弱的學生，更是存在較大困難。此時，“數形結合”能很好地把學生的生活經驗“數學化”。學生在創造他們個性化的“數學畫”的同時，他們的頭腦也在不斷地經歷“數學化”。

（二）當學生學習枯燥時

在數學教材中，數學的美無處不在。讓學生把數學的美“畫”出來，并及時地進行交流，學生非常喜歡這樣學，非常喜歡學這樣的數學。比如教學《平移和旋轉》和《軸對稱圖形》，筆者給學生提供了很多現實生活中的花邊，課后讓學生設計花邊。學生設計出來的那些美麗的作品讓筆者不由不感嘆孩子的創造力和想象力。通過這樣布置作業，筆者發現學生學數學的熱情高了，寫作業的興趣也高了。

（三）當學生思維受阻時

小學生的思維是由具體形象思維向抽象邏輯思維發展的關鍵時期，當學生的思維受阻時，通過畫一畫、議一議的過程，讓學生在畫的過程中更全面、更深入地理解問題，在合作交流中解決問題，發展數學思維。

總之，利用“數形結合”思想能使“數”與“形”有機統一起來，借助“形”的直觀來理解抽象的“數”，運用“數”與“式”來概括與抽象刻畫“形”的特征，直觀與抽象相互配合，取長補短，從而順利、高效地解決問題，完善數學結構。教師善于運用數形結合思想，多創造“數”與“形”的美麗邂逅，可以讓學生更喜歡數學，促進學生數學思維能力的發展，提升數學素養。

（責編 林 劍）