轉子偏心凸極永磁電機電樞磁場解析研究

曹晴，李槐樹，周羽，周石

（海軍工程大學電氣工程學院，武漢430033）

轉子偏心凸極永磁電機電樞磁場解析研究

曹晴，李槐樹，周羽，周石

（海軍工程大學電氣工程學院，武漢430033）

本文基于許-克變換針對轉子偏心凸極永磁電機建立了磁場計算模型。首先計算方波磁勢作用下電機的直、交軸電樞磁場；然后計算不規則磁勢分布條件下的直、交軸電樞磁場；電樞磁場即為兩者疊加。該方法適用于各種偏心情況下的電機磁場計算。將本模型計算的電樞磁場分布與有限元比較，結果吻合，證明其準確性和有效性。

轉子偏心凸極永磁電機直、交軸電樞磁場

0　引言

凸極永磁電機具有高功率密度、高過載能力、易于弱磁調速、調速范圍寬、突出的轉矩控制能力等優點。因此廣泛應用于風力發電、航空航天、數控加工以及新能源混合電動汽車等領域［2］。采用轉子偏心結構的凸極PMSM，氣隙不均勻，氣隙磁場中的諧波含量減小，因而電動勢和電流的諧波含量減小，附加的諧波鐵損和銅損減小，使得電機效率大幅提升［3-4］。轉子偏心凸極永磁電機結構復雜，利用有限元計算，電機結構參數改變時需重新建立模型，剖分網格，使用不夠便捷。解析計算法可方便快捷的進行電機結構參數的更改，優化電機性能。

現有運用解析法進行磁場計算和分析的研究，主要針對表貼式永磁電機，凸極永磁電機通常采用有限元法進行磁場計算，少有文獻對復雜結構的凸極永磁電機磁場計算提出一般的解析表達式。如文獻［5］采用解析法計算考慮開槽的分數槽集中繞組永磁同步電機電樞反應磁場，分析了不同極槽配合電機的電樞反應磁場的諧波成分和開槽對諧波成分和幅值的影響；文獻［6］采用解析法計算表貼式永磁電機空載氣隙磁場，求解拉普拉斯方程和泊松方程，通過矢量磁位求得氣隙磁通密度表達式；文獻［7］、［8］采用有限元數值計算得到嵌入式永磁電機的氣隙磁密波形，充分考慮電機的漏磁、飽和等因素的影響，計算精度高。為了簡化其磁場計算，方便電機結構參數調整，優化電機，有必要對此類結構復雜永磁電機電樞反應磁場的一般分布規律進行研究。

本文首先利用許克變換得到的隱函數公式分別推導了電樞磁勢為方波磁勢時直軸電樞磁場和交軸電樞磁場，以此為基礎求得不規則磁勢分布時的直、交軸電樞磁場在氣隙中的分布規律，最后通過與有限元法計算結果的對比分析，證明其有效性和準確性。

2　凸極永磁電機解析模型

為簡化計算，在不影響電機性能計算的前提下，作如下基本假定：

1）定轉子內表面光滑；

2）永磁體磁導率近似與空氣相等；

3）鐵心磁導率為無窮大；

4）忽略渦流和飽和效應。

轉子偏心凸極永磁同步電機的結構示意圖如圖1所示。點O為定子軸心，H為轉子極弧中心與電機軸心的偏心距離，Rs為定子內半徑，δmin定轉子間的最小氣隙長度，δ（θ）定轉子間不同氣隙空間角對應的氣隙長度，δmax定轉子間最大氣隙長度。

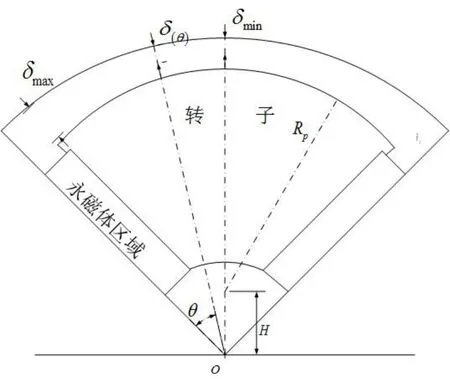
圖1　偏心凸極永磁同步電機的結構示意圖

3　電樞磁場解析計算

基于雙反應理論，電樞磁場包括直軸電樞磁場和交軸電樞磁場，兩者疊加即為電樞反應磁場。

3.1直軸電樞磁場解析計算

直軸磁路中由于永磁體的存在，當直軸磁勢作用于直軸磁路時，一部分降在氣隙上，一部分降在永磁體所占的區間。其走向分布見圖2。直軸電樞磁場由直軸電樞磁勢fd和轉子鐵心磁勢Fm共同作用產生，轉子鐵心磁勢Fm是與電樞磁勢大小相關的方波磁勢。區間I、II的磁通分別指直軸電樞磁勢fd、轉子鐵心磁勢Fm單獨作用時的磁通，兩者磁通的疊加即為氣隙部分磁通。

根據磁通的走向，由磁通連續性定理可知：

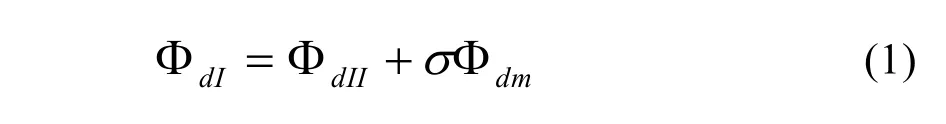
區間I的磁通ΦdI：

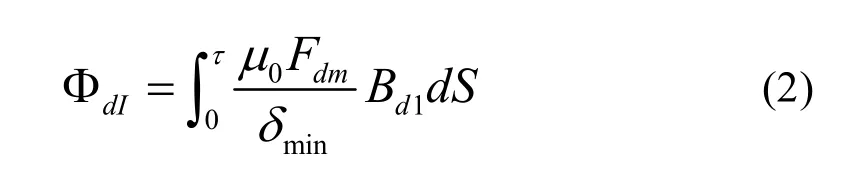
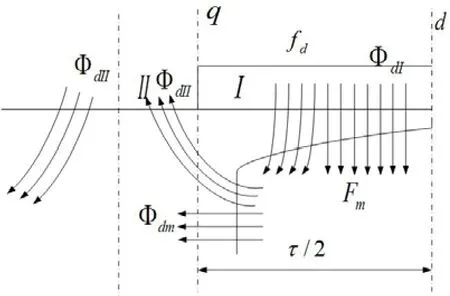
圖2　直軸磁通走向分布

區間II的磁通ΦdII：

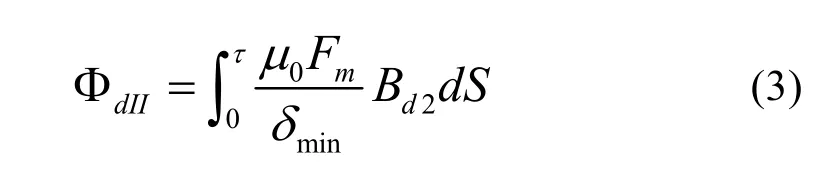
經過永磁體部分的磁通Φdm：

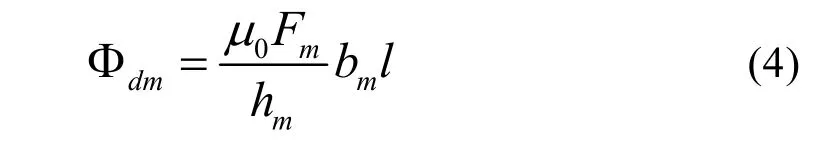
由（1）、（2）、（3）、（4）解得

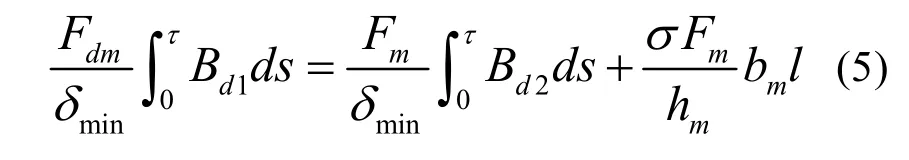
其中：σ為漏磁系數；μ0=4π×10-7為真空磁導率；Fdm為直軸電樞磁勢的最大值；Fm為鐵芯內部磁勢；Bd1為直軸電樞磁勢產生的磁通密度；Bd2為鐵心磁勢產生的磁通密度；l為電機軸向長度。

作用在氣隙上的磁動勢為方波磁勢時，在氣隙中產生的直軸相對磁通密度Bd，利用許克變換得到的直軸磁密隱函數公式（6）求得。

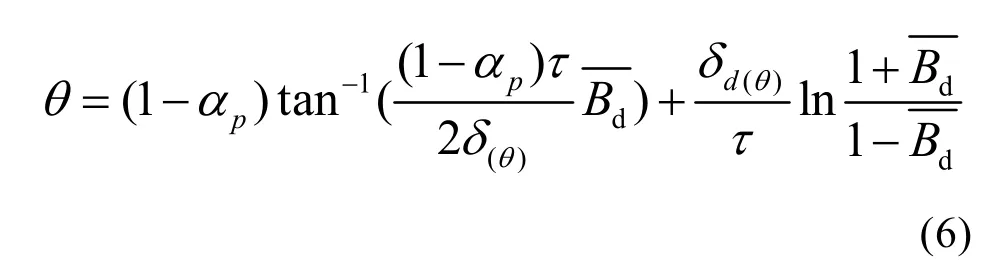
其中：θ為氣隙空間電角度；pα極弧系數；為極距，p為極對數；為得到的直軸相對磁通密度，相對磁通密度指最大磁通密度為“1”的磁通密度分布。

直軸電樞磁勢為方波時，直軸電樞磁勢產生的磁場和鐵芯磁勢產生的磁場在氣隙中的分布規律一致，只是幅值大小不相同，因而有：

實際運行中，電機直、交軸電樞磁勢并非為方波磁勢，而是隨著轉子位置的不一樣，呈不規則形狀分布，因此電機電樞磁場的計算，須考慮不同磁勢分布情況。

對于直軸電樞磁場，直軸電樞磁勢為任意磁勢時，直軸電樞磁勢作用產生的磁場和鐵芯磁勢產生的磁場在氣隙中的分布規律不一致，幅值大小也不相同，直軸電樞磁勢作用產生的磁場在氣隙中的分布規律與直軸電樞磁勢分布規律相關，而鐵心磁勢始終為方波磁勢，則其分布規律不變：

直軸電樞磁勢作用產生的磁場幅值和鐵芯磁勢作用產生磁場的幅值分別為：

則最終得到的直軸電樞磁勢為方波、任意波磁勢時，直軸電樞磁場的一般表達式分別為：

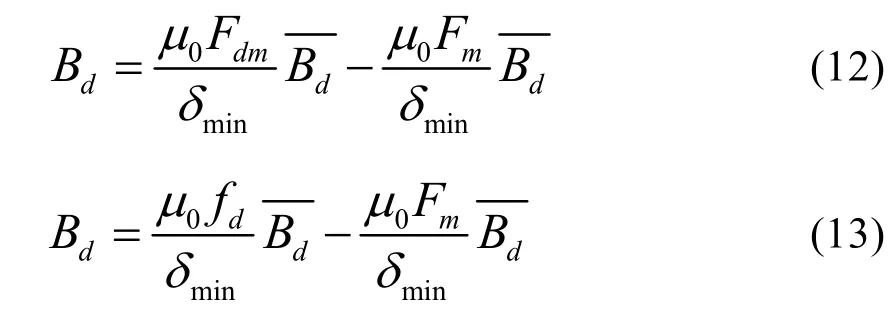
3.2交軸電樞磁場解析計算

作用在氣隙上的磁動勢為方波磁勢時，在氣隙中產生的交軸相對磁通密度，利用許克變換得到的交軸磁密隱函數公式（14）、（15）得到。

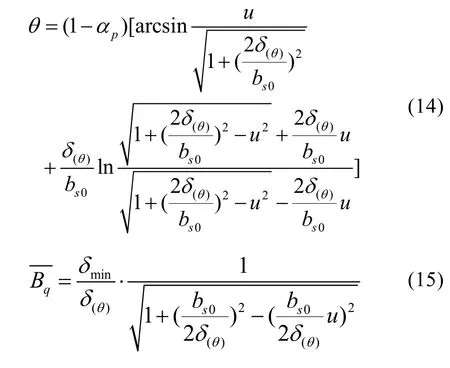
其中，u=0～1為中間變量，bs0為極間距。

交軸電樞磁勢為方波磁勢時產生的交軸磁場在氣隙中的分布為：

交軸電樞磁勢為任意磁勢時，產生的交軸磁場在氣隙中的分布與交軸電樞磁勢在氣隙中的分布有關，即：

其中，fq為交軸電樞磁勢，Fqm為交軸電樞磁勢的最大值。

此時，交軸電樞磁勢作用產生磁場的幅值：

最終得到交軸電樞磁勢為方波、任意波磁勢時，交軸電樞磁場的一般表達式分別為：

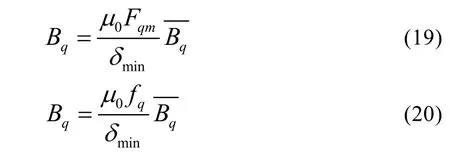
4　解析法與有限元法結果對比分析

凸極永磁同步電機磁場的實驗驗證不方便實施，采用被大家認可的有限元的方法驗證此方法的準確性。解析計算方法得到的結果與相應的有限元的方法得到的結果相吻合，則可證得解析計算方法的準確性。以4極48槽的凸極永磁電機樣機為算例進行驗證。偏心凸極永磁電機主要結構尺寸參見表1。

表1　偏心凸極永磁電機主要結構尺寸

直、交軸有限元計算模型如圖3（a）、（c）所示。解析法與有限元法得到的電樞磁場在氣隙空間的分布規律的對比如圖3（b）、（d）所示。由于定子開槽的影響，有限元計算波形在施加電流位置會有較大突變，而采用解析法計算的直、交軸電樞磁場磁密波形與有限元計算出的磁密波形僅在施加電流的位置有差異，其余位置均能較好吻合。

有限元計算得出的波形在施加電流位置會有較大突變的原因在于有限元開槽的槽口邊緣聚磁效應導致高次諧波幅值加大，使得開槽點磁密出現大的突變，當不考慮開槽影響時，突變也就不存在了，而本文解析計算方法不考慮開槽的影響，因而兩者波形在槽口施加電流處會有一定差別。磁密的計算是為了分析計算電機電感參數和電機性能，通常開槽影響可通過卡氏系數進行修正。

5　總結

本文利用許-克變換得到的隱函數公式，采用基于方波磁勢磁場的解析計算方法來進行轉子偏心凸極永磁電機的磁場解析研究，以一臺4極48槽的電機為樣機，計算電機交直軸電樞反應磁場，并通過與有限元數值計算的對比，驗證了該方法的準確性和有效性。

該方法具有如下優勢：1.能夠方便快捷、準確有效地進行復雜結構嵌入式永磁電機的磁場計算；2.針對電機的不同性能要求，可快速有效地進行電機結構參數的更改，利于電機的優化設計。

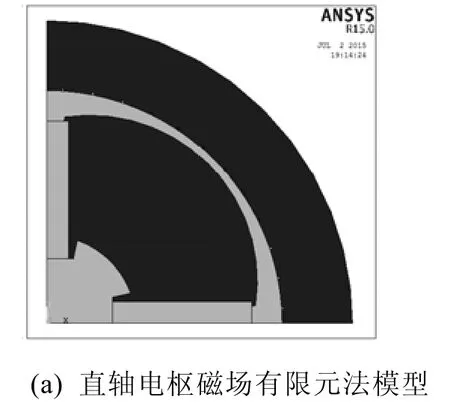
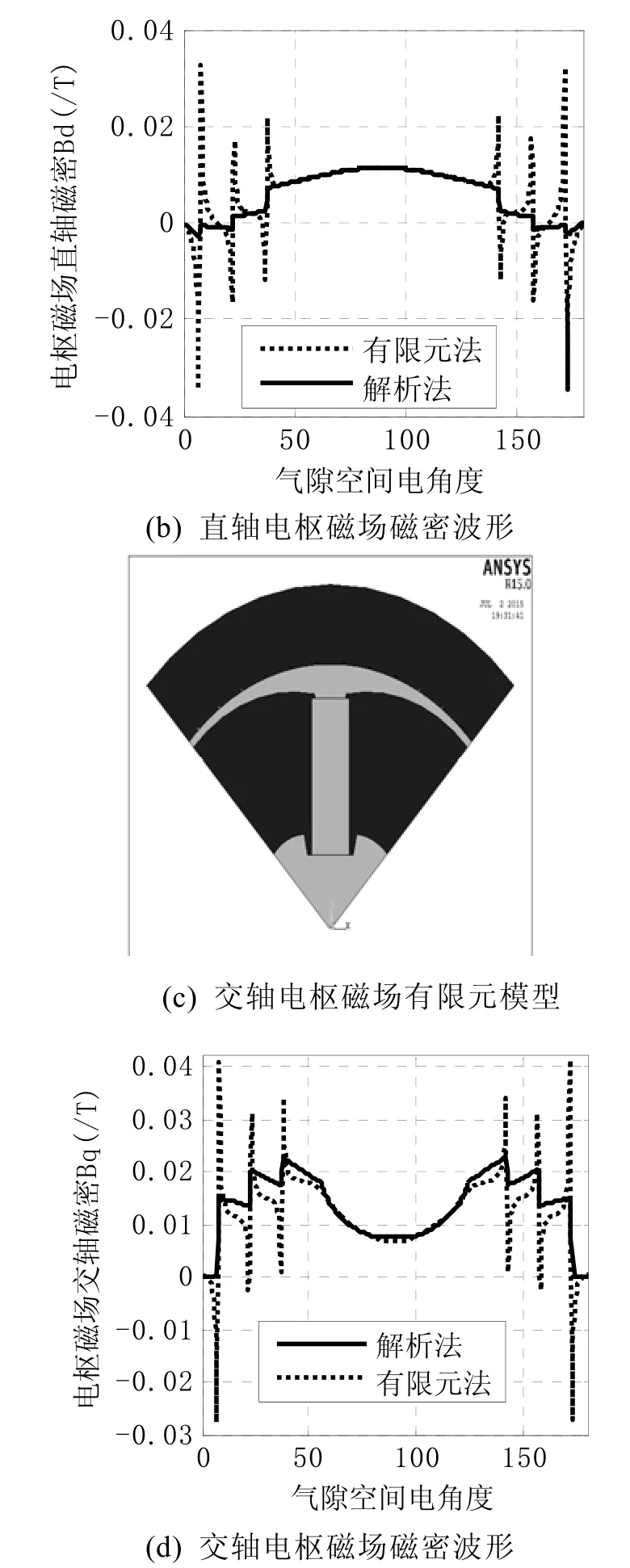
圖3　解析法與有限元法電樞磁場對比

［1］王慶春.表面磁體永磁電機主磁場的分布特性［J］.船電技術，2000，（1）：17-21.

［2］吳海鷹.永磁電機電磁計算［J］.船電技術，2004，（5）：18-22.

［3］黃克峰，李槐樹，金朝紅，李帥.低速大推力圓筒永磁直線電動機磁場分析［J］.微特電機，2012，40（2）：4-6.

［4］黃克峰，李槐樹，周羽.三相切向結構永磁電動機電感參數解析計算［J］.微特電機，2010，（7）：7-11.[5]林福,左曙光,馬琮淦,譚欽文.考慮開槽的分數槽集中繞組永磁同步電機電樞反應磁場解析計算[J].電工技術學報,2014,29（5）:29-35.

[6]章躍進,江建中,屠關鎮.應用數值解析結合法計算旋轉電機磁場[J].電工技術學報,2004,19（1）: 7-11.

[7]陳超,劉明基,張健,陳偉華,羅應立.利用不均勻氣隙優化自起動永磁電機的氣隙磁密波形[J].電機控制與應用,2010,37（7）:1-5.

[8]王玉彬,孫建鑫.分數槽集中繞組嵌入式永磁同步電機設計[J].電工技術學報,2014,29（5）:70-75.

[9]石有計.內置式永磁同步電動機電感參數計算分析[J].微特電機,2014,42（4）:4-7.

[10]ChauKT,ChanCC,LiuC.Overviewof permanentmagnet brushless drives for electric and hybrid electricVehicles[J].IEEE Transactions on Industrial Electronics,2008,55(6):2246-2257.

Analyticalstudy on Calculating Armature-reaction Field ofsalient PMSM with Eccentric Rotor

Cao Qing，Li Huaishu，Zhou Yu，Zhoushi
（College of Electrical Engineering，Naval University of Engineering，Wuhan 430033，China）

Models based onschwarz-Christoffel's transformation of asalient PMSM with rotor eccentricity is presented.At first，motor's direct-quadrature（d-q）axis's armature-reaction field undersquare wave magnetomotive force is calculated.Then，d-q armature-reaction field under magnetomotive force without regular distribution is analyzed.Finally，armature-reaction field can be obtained bysuperposing them.This method can be applied to magnet calculation of different types of motors with rotor eccentricity. Armature-reaction field of this motor was calculated by using this analytical method and Finite Element Method（FEM）.The resultsshows that the two cases agree well，and theValidity and accuracy of the presented method areVerified.

eccentric rotor；salient PMSM；d-q axis；armature-reaction field

TM351

A

1003-4862（2015）10-0074-04

2015-08-25

曹晴（1990-），女，碩士研究生。研究方向：異步起動永磁同步電動機。