雙馬達回轉同步驅動系統建模與控制研究

劉湘琪　蒙　臻　倪　敬　朱澤飛

1.浙江理工大學，杭州，310018　　2.杭州電子科技大學，杭州，310018

雙馬達回轉同步驅動系統建模與控制研究

劉湘琪1，2蒙臻1倪敬2朱澤飛2

1.浙江理工大學，杭州，3100182.杭州電子科技大學，杭州，310018

針對雙液壓馬達回轉高性能同步驅動問題，引入無阻尼行星系齒輪傳動彈性動力學理論，基于雙液壓馬達回轉運動特性建立了系統非線性動力學模型；針對回轉系統跟蹤性能和同步性能要求，引入迭代學習控制算法(ILC)，提出了結合離散化PID控制器結構的IL-PID同步控制策略。該控制策略基于“等同式”同步控制原理，在各單通道內部采用獨立的離散化PID控制實現系統跟蹤性能，在多通道間采用基于閉環D型學習律的IL控制實現系統同步性能。在五自由度液壓伺服機械手上的實際應用結果表明，該控制策略相比于傳統的PID控制具有較好的跟蹤性能和同步驅動性能。

雙液壓馬達回轉驅動模型；迭代學習控制算法(ILC)；IL-PID同步控制；電液伺服驅動

0　引言

多驅動回轉系統是采用多執行器協同驅動實現運動部件相對回轉的裝置，廣泛應用于盾構機、塔式起重機、挖掘機等大型工程機械以及多軸飛行仿真轉臺等高技術設備中。目前，多驅動回轉系統主要采用多電機回轉驅動形式和多液壓馬達回轉驅動形式。多電機驅動形式采用多個交流電動機經減速器驅動回轉裝置，具有傳動效率高、運行噪聲小、可維護性好等特點,其缺點是執行器體積較大、安裝配合精度要求較高、制動性能較差，當驅動負載發生較大的波動時，執行器容易因剛性過載而發生故障。多液壓馬達回轉驅動形式雖然傳動效率較低，但液壓驅動的功率密度比電機驅動的功率密度大[1]，在滿足驅動功率的前提下，可以優化執行器體積，合理利用回轉系統的內部空間，降低回轉系統的制造成本，同時還能在很大程度上消除和抑制負載擾動因素的影響[2]，因此，研究多液壓馬達驅動回轉機構動力學特性及系統響應特性具有重要的實際意義。

國內外許多學者在多驅動回轉系統建模與控制方面進行了相關研究。Ali等[3]受生物大腦情緒學習的啟發，針對閥控電液伺服馬達定位控制問題，通過遞歸最小二乘法辨識馬達模型參數，并基于該模型設計了情緒學習智能控制器，采用在線實時學習優化控制參數，實現系統高精度定位性能；Hossam等[4]采用LS-SVM方法辨識離線閥控液壓馬達系統，然后基于仿真測試控制器參數和速度表數據，設計了閥控液壓馬達系統的速度控制器；郭治富等[5]針對三軸仿真轉臺的兩個閥控馬達子系統同步問題，設計了一種模型參數辨識控制器，通過灰箱辨識來獲得同步子系統的實際模型參數，為同步控制設計提供幫助；張今朝等[6]針對多電機同步系統的強耦合、非線性特性，采用局部模型網絡的多模型建模方法，通過加權綜合線性子模型，最終得出了速度和張力的全局模型；鄧先榮[7]針對天線伺服系統多電機驅動時容易激發差速振蕩的問題，提出了和速負反饋控制法等同步的控制方法，實現轉速、電流雙閉環調速控制系統多電機的轉速同步控制；王麗梅等[8]針對雙直線電機同步驅動機械耦合問題，設計了解耦控制器，使系統具有較高的響應能力。但上述研究一方面大多偏重于針對閥控馬達的線性特性建模，對多馬達回轉系統的動力學描述較為模糊，所建立的模型不夠細致；另一方面大多集中于電氣驅動領域，偏重于設計伺服電機同步驅動控制方式；還有所設計的智能控制算法停留在理論研究實驗階段，不易實現。因此，開展多馬達回轉同步驅動系統建模與控制研究十分必要。

本文以五自由度(degree of freedom,DOF)液壓伺服機械手的雙馬達回轉同步驅動系統為測試平臺，引入了忽略阻尼作用的簡化型行星齒輪彈性驅動理論和非線性閥控液壓馬達理論，建立了實際系統動力學模型，引入迭代學習(iterative learning,IL)原理，提出了一種IL-PID同步控制策略，并通過仿真和實際應用驗證了該控制策略的有效性。

1　系統模型

液壓機械手系統如圖1所示，主要由夾取系統、俯仰系統、推拉系統及回轉系統組成。雙馬達回轉系統如圖2所示，主要由驅動部分、支撐部分以及轉體部分組成。其中驅動部分包括兩個液壓馬達，以及同軸連接的等參數驅動齒輪，由電液比例閥對液壓馬達進行控制；支撐部分包括底座以及固定在底座上的傳動外齒圈；轉體部分包括回轉平臺與轉軸，且驅動部分的馬達安裝于回轉平臺上，轉軸與底座通過軸承連接。該回轉系統工作原理為：采用外嚙合的驅動方式，由2個液壓馬達伺服同步驅動等參數驅動齒輪，基于外齒圈嚙合的反作用力矩實現回轉運動。

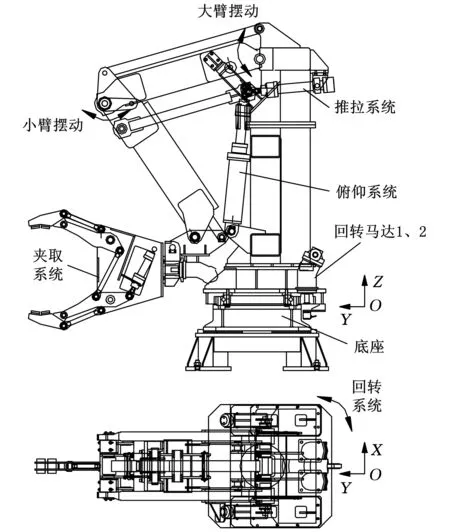
圖1　5DOF液壓伺服機械手機構圖

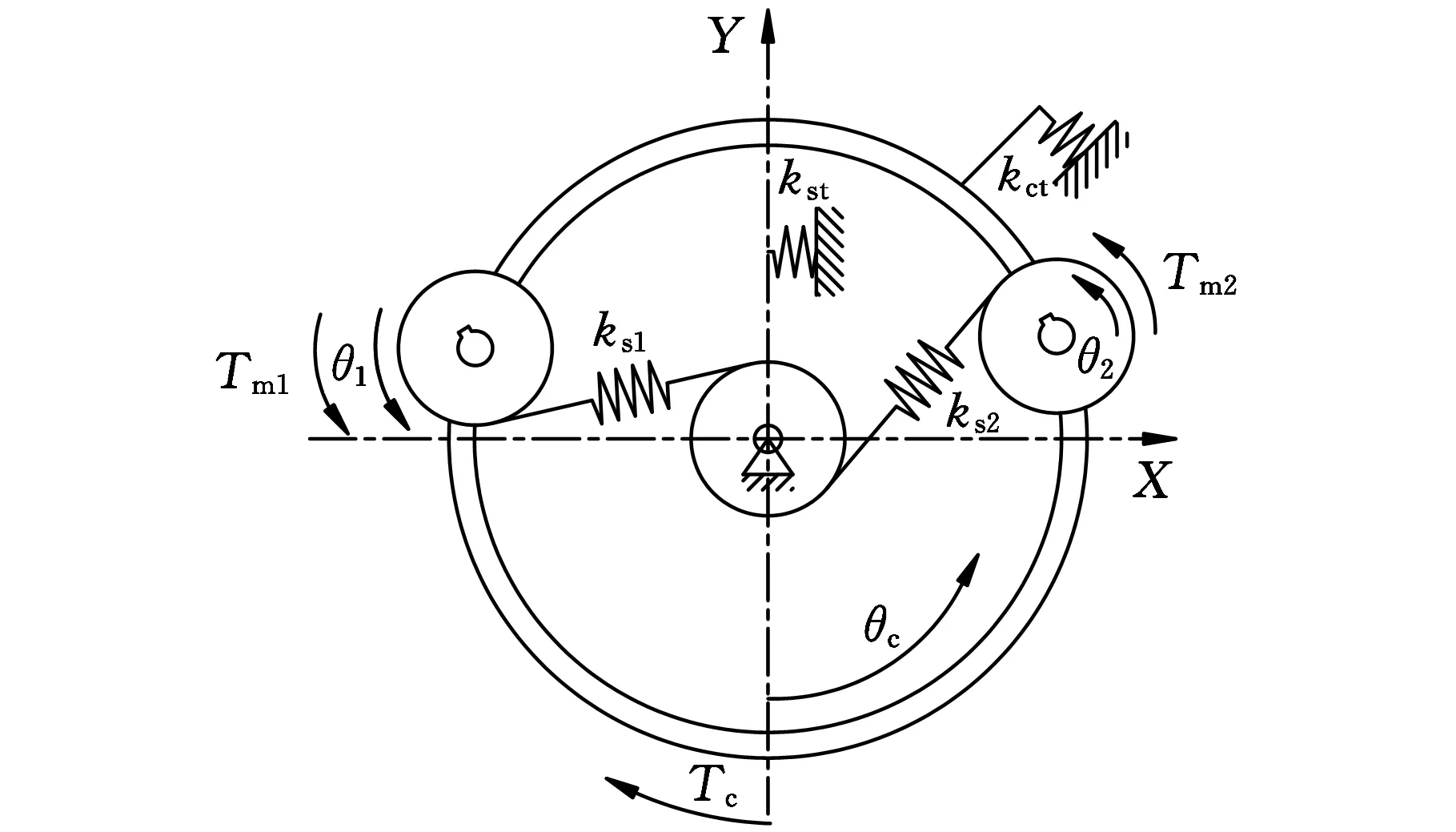
圖3　驅動部分行星傳動系統模型

如果只考慮驅動部分，可以將雙馬達回轉系統簡化為圖3所示模型。圖中，θ1、θ2分別為驅動齒輪1、2的角位移，由于機械結構中驅動齒輪與液壓馬達輸出軸同軸直連，因此可將θ1和θ2視作液壓馬達1、液壓馬達2輸出軸的角位移進行研究(液壓馬達1、2分別由各通道比例閥控制)；θc為回轉平臺的角位移，在本文中視作行星傳動系桿的角位移進行研究；kit(i=c，s)為構件的切向支承剛度；ksn(n=1，2)為齒輪外嚙合的時變嚙合剛度；Tc為系統折算到系桿上的負載力矩，N·m；Tm1、Tm2分別為兩驅動齒輪的驅動力矩，亦是折算到兩液壓馬達軸上的負載轉矩，N·m。

1.1馬達同步驅動過程動力學方程

如圖2所示的行星傳動系統，其動力學特性較為復雜。為了便于研究，本系統忽略阻尼作用，僅考慮各構件扭轉振動，根據各構件的受力以及牛頓第二定律建立系統的動力學方程如下[9]：

(1)

δsn=(θn-θccosα)+esn(t)

式中，Jc為系桿的轉動慣量，kg·m2；Jm1、Jm2分別為兩驅動齒輪的轉動慣量，kg·m2；m1、m2分別為兩液壓馬達及驅動齒輪的質量，kg；R為系桿中心半徑，mm；r為兩驅動齒輪半徑，mm；α為齒輪嚙合角；δsn(n=1,2)為外齒圈相對于第n個驅動齒輪的位移沿外嚙合方向的投影；θn(n=1,2)為第n個驅動齒輪的角位移，rad；esn(n=1,2)為第n個驅動齒輪與外齒圈的綜合嚙合誤差，rad。

1.2馬達角位移與回轉角位移耦合關系

在運動過程中，由于冗余驅動的耦合作用，嚙合系統會沿著系桿產生一個基于驅動齒輪1、2旋轉中心的耦合力矩。類比三自由度集中質量系統線彈性耦合作用，可得驅動齒輪轉角θ1、θ2和回轉平臺轉角θc有如下關系：

(2)

1.3單通道馬達力矩平衡方程

根據力矩平衡原理以及式(1)可得單通道馬達的力矩平衡方程為

(3)

j=1, 2

式中,Bmj為第j個液壓馬達的等效黏性阻尼系數，N·s/m；Jj為第j個液壓馬達軸的轉動慣量，kg·m2；Dmj為第j個液壓馬達的排量，m3/(Pa·s)。

1.4單通道馬達負載流量方程

根據文獻[10]，以液壓馬達為研究對象，第j個液壓馬達的負載流量方程如下：

(4)

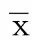
1.5單通道馬達流量連續性方程

根據文獻[10]，非對稱閥控液壓馬達的流量連續性方程為

(5)

式中,Vtj為第j個液壓馬達的有效容積，m3；Ctj為第j個液壓馬達的泄漏系數；βe為系統的有效容積模數。

1.6雙馬達回轉系統數學模型

由式(1)～式(5)，選取θ=[θ1θ2pL1pL2]T，這樣可得到所求的雙馬達回轉系統的數學模型如下：

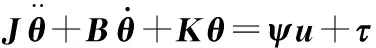
(6)

u=[00u1u2]T

τ=[-Tcr/(2Rcosα)-Tcr/(2Rcosα)00]T

Jz=(Jc+m1R+m2R)r2/(2R2kctθc)

式中，u為系統控制輸入；τ為系統擾動；Kj為控制輸入增益。

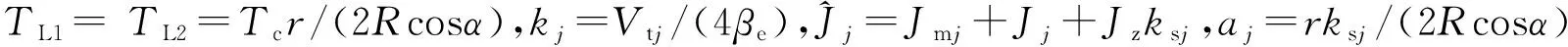
2　系統IL-PID同步控制研究

2.1IL-PID同步控制策略分析

如式(6)和圖4所示的雙馬達回轉同步驅動模型具有較強的非線性耦合特性，且未知信息較多，常規驅動控制方式難以實現跟蹤精度要求。因此受文獻[11]的啟發，針對本系統所具有的重復回轉運行特性，借鑒具有無需辨識系統參數、適用于重復運動系統等特點的IL(iterative learning)算法，結合“等同式”PID構建了圖5所示的IL-PID雙馬達同步控制策略。圖中，r為指令輸入值；e1和e2分別是第1、2通道的跟蹤誤差量；

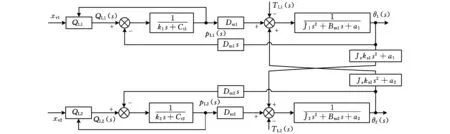
圖4　雙馬達回轉驅動系統模型

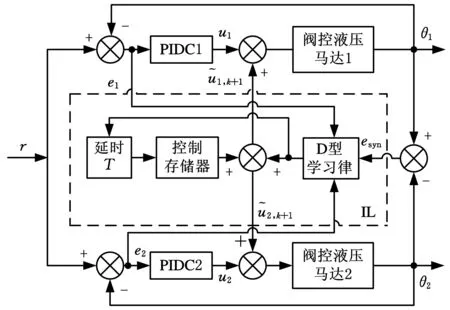
圖5　IL-PID同步控制策略原理圖

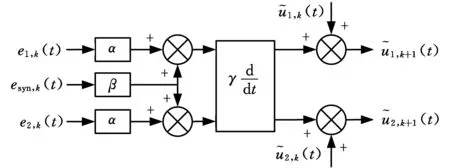
圖6　D型學習律

2.2具體IL-PID同步控制器設計

根據上述控制策略的分析，控制器設計過程分為如下幾步。

(1)PID算法離散化。第j個通道的PID控制輸出uj可表示為

(7)

式中，KPj、KIj、KDj分別為第j個通道的PID控制器的比例、積分和微分參數；Δt為采樣時間間隔。

(8)

基于離散化處理，可將式(8)改寫為

(9)

(3)迭代截止條件。構建的式(9)所示的學習律，在系統每次重復運行后，都必須檢驗迭代截止條件：|esyn|<ε1、|ej|<ε2。另外，通過限制最大迭代次數k≤kmax，也能停止迭代。

(4)控制輸出。結合式(7)和式(9)，可得IL-PID同步控制器的輸出為

(10)

(5)IL-PID控制器參數取值條件。系統的狀態方程為

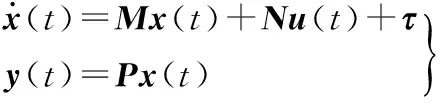
(11)

式中，x(t)、u(t)、y(t)分別為系統的狀態向量、輸入向量和輸出向量，均為2維；M、N、P為具有適當維數的矩陣函數，其中，M=[0 1 K/J B/J]，N=[0 ψ/J]T，P=[1 0]。

因此，IL-PID控制器的參數α、β和γ雖然通常采用系統調試過程中的經驗數據，但其取值必須滿足系統收斂的必要條件[11]：

ρ([I+(α+β)γPM]-1)t=0<1

(12)

3　系統仿真與實驗研究

本文研究涉及的5DOF液壓伺服機械手的雙馬達回轉同步驅動平臺實物如圖7所示，其中圖7a為5DOF液壓伺服機械手實物，圖7b為機械手運動伺服控制系統，主要元件及參數為：液壓油源工作壓力8MPa，工作流量100L/min，圖1所示的機械手俯仰系統工作角度為0°～33°，機械手最大夾持負載為1000kg，液壓馬達型號為A2FM56/61W、絕對位置旋轉編碼器型號為E6B2-C、力士樂比例伺服閥型號為4WRZE10-75、脈沖計數模塊、DA模塊、研華工控機。根據文獻[12]，系統其他參數如表1所示。

(a)5DOF液壓機械手(b)伺服控制系統圖7　5DOF液壓伺服機械手系統

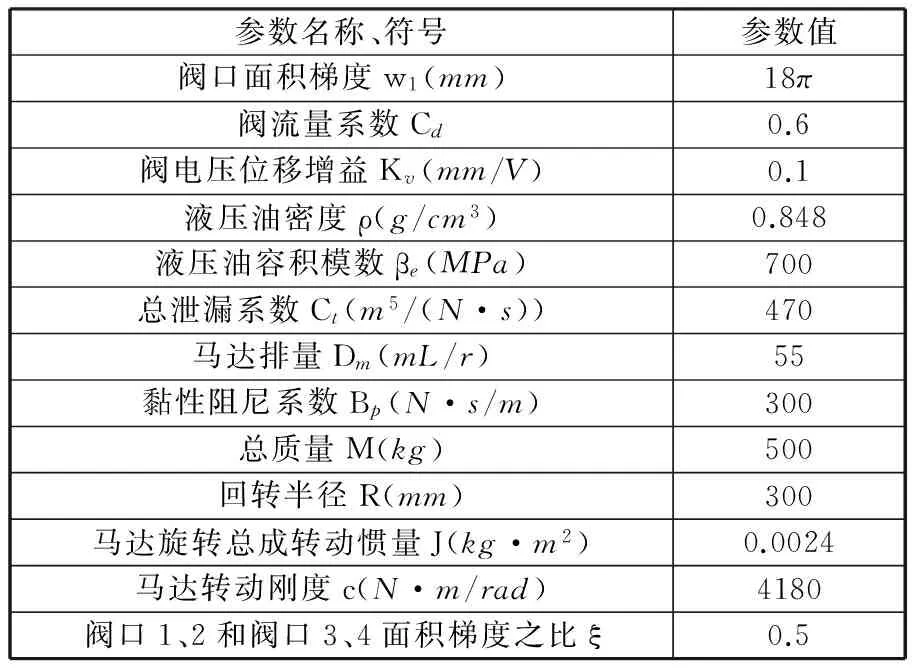
參數名稱、符號參數值閥口面積梯度w1(mm)18π閥流量系數Cd0.6閥電壓位移增益Kv(mm/V)0.1液壓油密度ρ(g/cm3)0.848液壓油容積模數βe(MPa)700總泄漏系數Ct(m5/(N·s))470馬達排量Dm(mL/r)55黏性阻尼系數Bp(N·s/m)300總質量M(kg)500回轉半徑R(mm)300馬達旋轉總成轉動慣量J(kg·m2)0.0024馬達轉動剛度c(N·m/rad)4180閥口1、2和閥口3、4面積梯度之比ξ0.5

為了檢驗IL-PID同步控制器的有效性，以常規PID同步控制器為對比對象，選取5DOF液壓伺服機械手穩定工作狀態為研究工況：系統在±1.5rad的范圍內循環運行，加速時間為0.5s，運轉速度設定為200rad/min(本文研究涉及的液壓伺服機械手最大回轉速度)，同步控制器參數如表2所示。

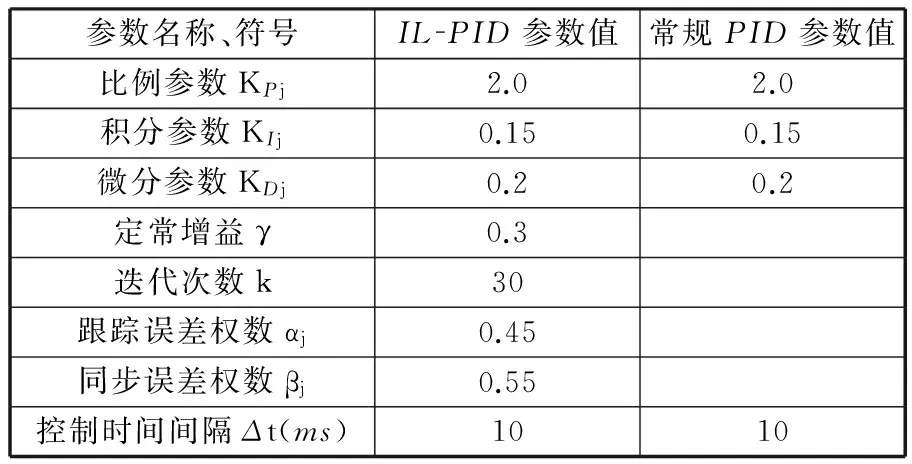
表2　控制器參數表

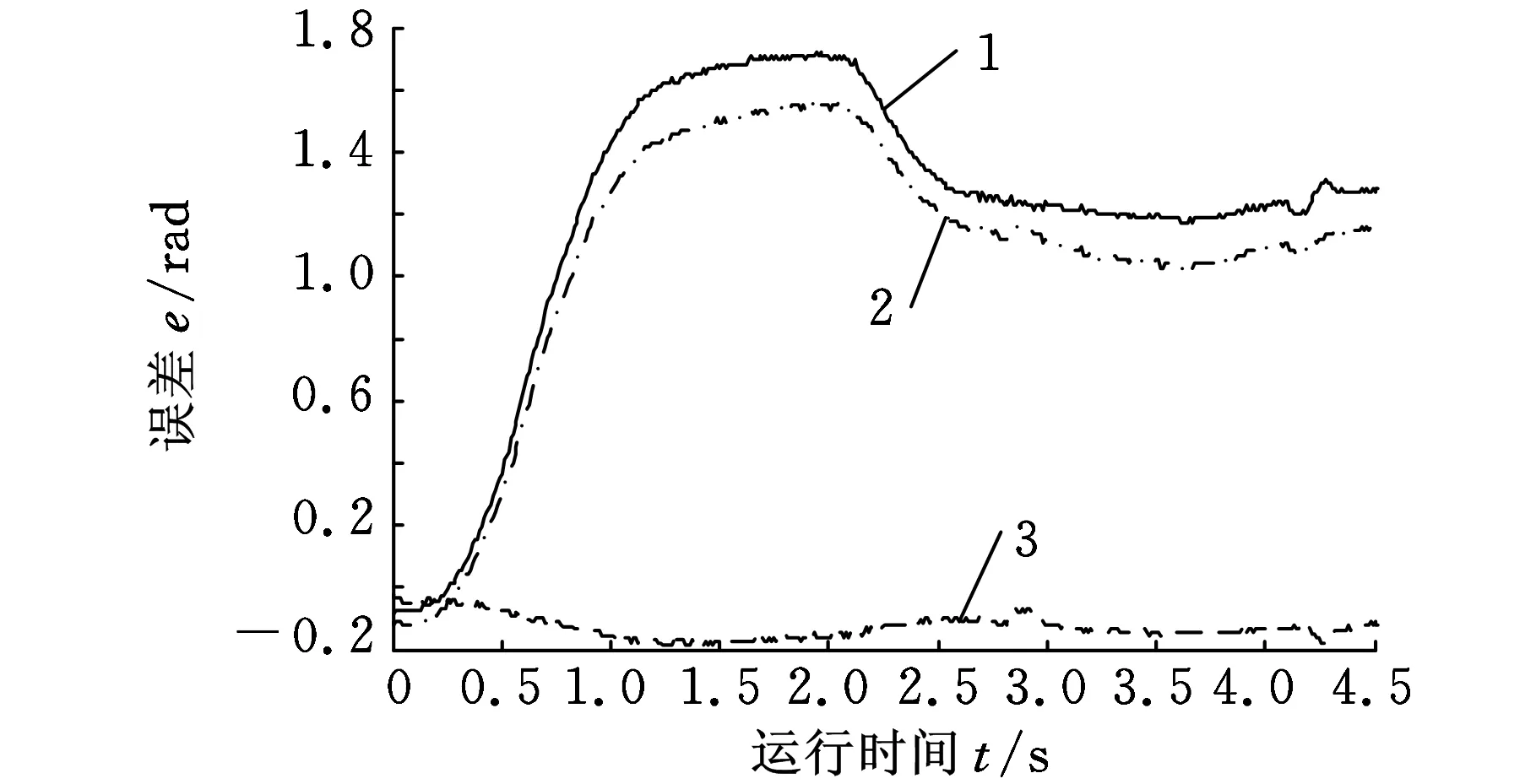
兩種控制策略的實際應用結果如圖8～圖11所示。圖12顯示了IL-PID同步控制器對于系統每次運行的最大同步誤差值esyn在30次迭代中輸出的過程。

1.液壓馬達1的跟蹤誤差　2.液壓馬達2的跟蹤誤差　3.兩馬達的同步誤差圖9　回轉系統PID同步控制實際運行結果

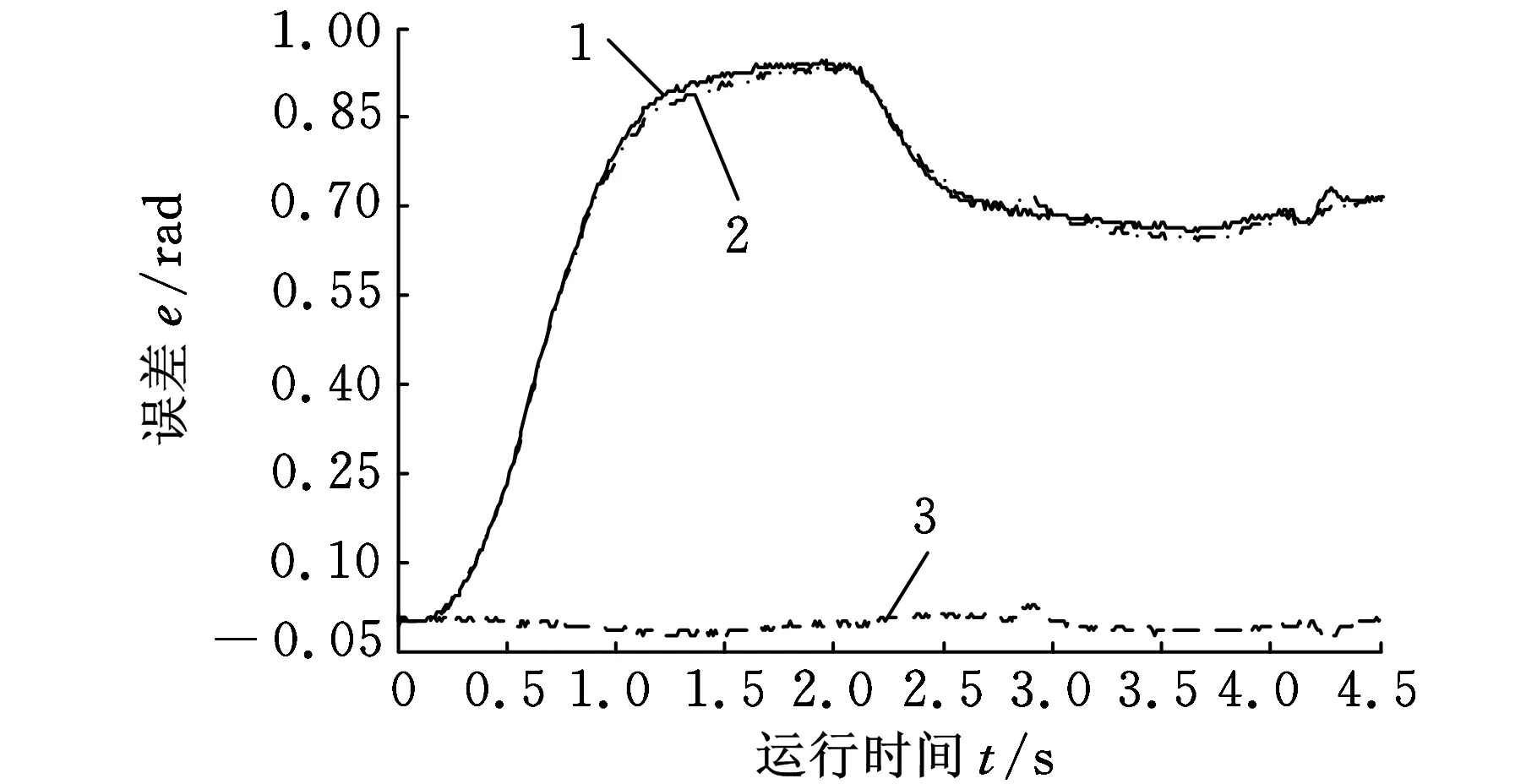
1.液壓馬達1的跟蹤誤差　2.液壓馬達2的跟蹤誤差　3.兩馬達的同步誤差圖10　回轉系統IL-PID同步控制仿真運行結果

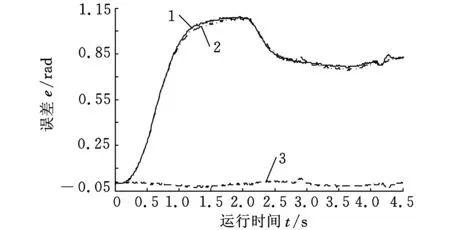
1.液壓馬達1的跟蹤誤差　2.液壓馬達2的跟蹤誤差　3.兩馬達的同步誤差圖11　回轉系統IL-PID同步控制實際運行結果

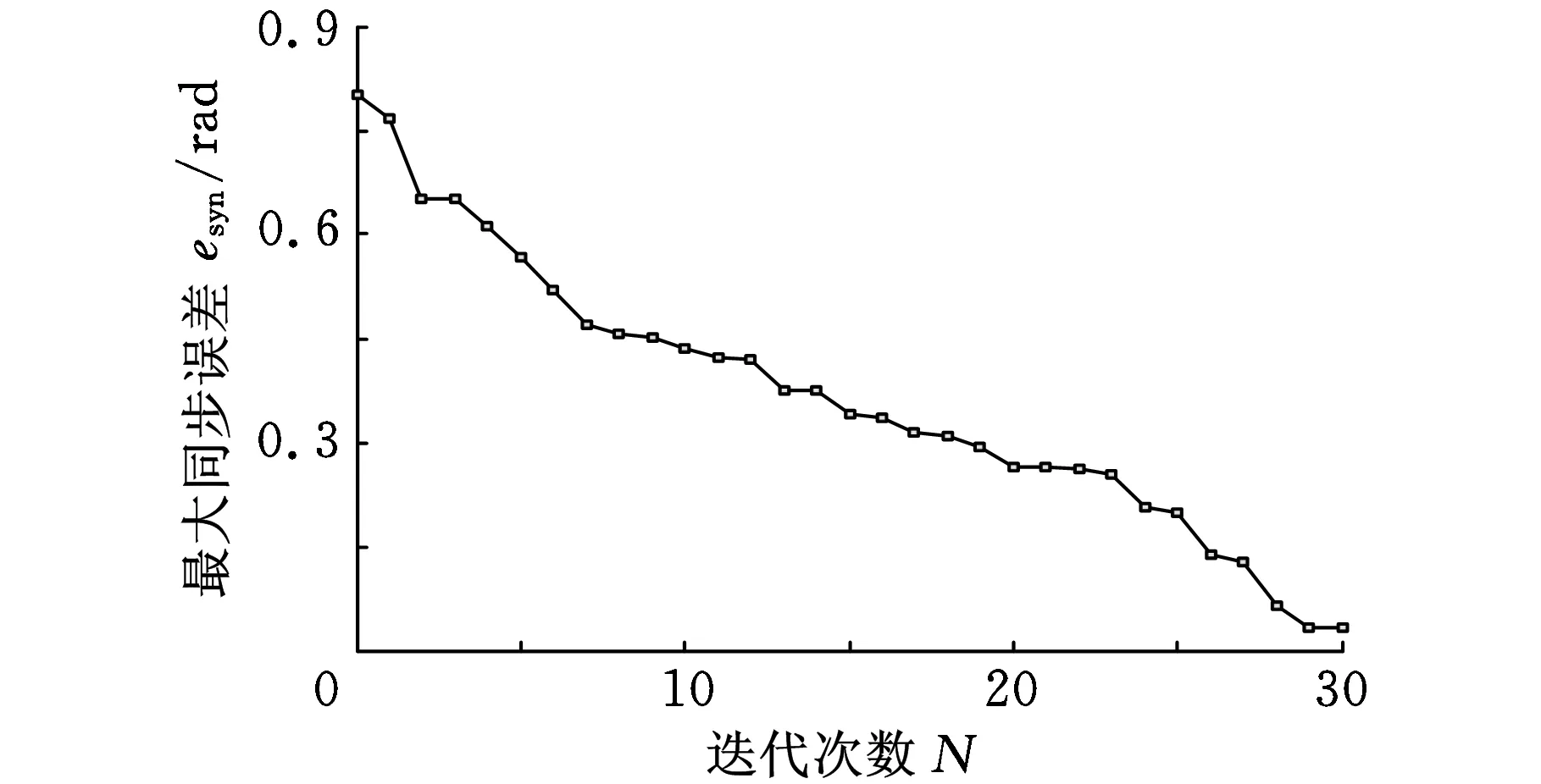
圖12　回轉系統IL-PID同步誤差修正動態過程

對比圖8與圖9可以看出，常規PID同步控制仿真與實際運行過程中，液壓馬達1和液壓馬達2的跟蹤誤差基本一致(相差在0.2rad以內)，液壓馬達1和和液壓馬達2的同步誤差基本一致(在±0.2rad之內)。

對比圖10和圖11可以看出，IL-PID同步控制仿真與實際運行過程中，液壓馬達1和液壓馬達2的跟蹤誤差基本一致(相差在0.15rad以內)，液壓馬達1和和液壓馬達2的同步誤差基本一致(在±0.05rad之內)。

對比圖8和圖10可以看出，在系統仿真控制情況下，IL-PID同步控制器的液壓馬達1和液壓馬達2的跟蹤誤差降低到區間[0.7，0.9]rad內，雙馬達同步誤差在±0.05rad左右，比常規PID同步控制器的各馬達跟蹤誤差小了0.6rad，雙馬達同步誤差減小了0.15rad。這就說明，IL-PID同步控制器比常規PID同步控制器具有更快的跟蹤響應速度和更好的雙馬達同步性能。

對比圖9和圖11可以看出，在系統實際控制情況下，IL-PID同步控制器的液壓馬達1和液壓馬達2的跟蹤誤差降低到區間[0.85，1.15]rad內，雙馬達同步誤差在±0.05rad左右，比常規PID同步控制器的各馬達跟蹤誤差減小了0.5rad，雙馬達同步誤差減小了0.15rad。這就說明，IL-PID同步控制器比常規PID同步控制器具有更快的跟蹤響應速度和更好的雙馬達同步性能。

從圖12可以看出，IL-PID同步控制器對于雙馬達的同步誤差修正效果是一個動態過程。在每次系統同步驅動過程中，控制器基于上一次運行效果為經驗模型，產生如圖11所示的同步誤差修正過程，從而在無需人工修改控制器PID控制參數的前提下，達到系統自我同步誤差修正的目的。

綜上所述，IL-PID同步控制器比常規PID同步控制器具有更快的跟蹤響應速度和更好的雙馬達同步性能。

4　結論

(1)本文結合簡化型行星齒輪彈性驅動理論和非線性閥控液壓馬達理論，建立了雙馬達回轉驅動系統模型，結合IL算法，提出了一種IL-PID同步控制策略，并將它實際應用到5DOF液壓伺服機械手中。

(2)通過常規PID和IL-PID同步控制器在實際5DOF液壓伺服機械手中的雙馬達回轉同步驅動平臺控制結果對比，得出IL-PID同步控制器比常規PID同步控制器具有更好的系統跟蹤性能和同步驅動性能的結論。

(3)提出的IL-PID同步控制策略不僅對于雙馬達回轉同步驅動系統具有良好的控制效果，還可適用于其他高度重復運行MIMO系統的同步控制中。

[1]錢冰哲, 潘高星. 恒壓閉式靜壓轉臺液壓系統設計[J].液壓氣動與密封, 2013(4)：18-20.

QianBingzhe,PanGaoxing.DesignoftheHydraulicSystemforClose-typeHydrostaticRotaryWorktable[J].HydraulicsPneumatics&Seals, 2013, (4)：18-20.

[2]張光譜, 陳其林, 陳宇華. 液壓等分回轉臺的設計應用[J]. 產品開發與設計, 2013, 40(4)：67-70.

ZhangGuangpu,ChenQilin,ChenYuhua.TheDesignandApplicationofHydraulicDirectRotaryTable[J].Machinery, 2013, 40(4)：67-70.

[3]AliS,HadiS,KamyarG,etal.IdentificationandReal-timePositionControlofaSero-hydraulicRotaryActuatorbyMeansofaNeurobiologically

Motivated Algorithm[J]. ISA Transactions, 2012, 51：208-219.

[4]Hossam M K, Mohammad E B. Implementation of Speed Controller for Rotary Hydraulic Motor Basaed on LS-SVM[J]. Expert Systems with Applications, 2011, 38：14249-14256.

[5]郭治富, 王榮, 趙克定. 基于參數辨識的雙馬達同步驅動控制研究[J]. 機床與液壓, 2008, 36(5)：119-121.

Guo Zhifu, Wang Rong, Zhao Keding. Research on Dual-motor Driven Servo System Based on Parameter Identification[J]. Machine tool & Hydraulics, 2008, 36(5)：119-121.

[6]張今朝, 劉國海, 潘天紅. 多電機同步系統的多模型辨識[J]. 電機與控制學報, 2009, 13(1)：138-142.

Zhang Jinzhao, Liu Guohai, Pan Tianhong. Multi-model Identification to Multi-motor Synchronous System[J]. Electric Machines and Control, 2009, 13(1)：138-142.

[7]鄧先榮. 天線伺服系統多電機同步控制方法[J]. 現代雷達, 2005, 27(6)：45-51.

Deng Xianrong. Methods of Synchronization Control with Multi-motor Drivers in Antenna Servo System[J]. Modem Radar, 2005, 27(6)：45-51.

[8]王麗梅, 黃飛. 雙直線電機同步驅動技術的研究[J]. 電氣傳動, 2009, 39(6)：51-54.

Wang Limei, Huang Fei. Research on Synchrodrive Technique of Dual Linear Motors[J]. Electric Drive, 2009, 39(6)：51-54.

[9]張策. 機械動力學[M]. 北京：高等教育出版社, 2008.

[10]倪敬. 電液伺服同步驅動系統控制理論與應用[M]. 北京：機械工業出版社, 2013.

[11]于少娟, 齊向東, 吳聚華.迭代學習控制理論及應用[M]. 北京：機械工業出版社, 2005.

[12]成大先. 機械設計手冊[M]. 5版.北京：化學工業出版社, 2011.

(編輯王艷麗)

Modeling and Synchronous Control on Rotary System with Dual Motor

Liu Xiangqi1，2Meng Zhen1Ni Jing2Zhu Zefei2

1.Zhejiang Sci-Tech University，Hangzhou,310018 2.Hangzhou Dianzi University，Hangzhou,310018

Aimed at the high performance synchronous driving problem of dual hydrauic motors rotation，the elasticity theory of undamped planetary gear transmission was introduced. On the basis of analyzing the movement characteristics of dual motors hydraulic rotation system, the nonlinear model was established. For the rotation system index requirements of tracking performance and synchronization performance, ILC algorithm was introduced, and the IL-PID servo synchronization control strategy with the combination of discrete PID controller structure was proposed. This control strategy was based on “equivalent” type synchronous control principle, independent discrete PID control was adopted to realize the system tracking performance within each single channel,the IL control which was based on closed-loop D-type learning law was adopted to realize the system synchronization performance among the multi-channels. The results of practical applications on 5-DOF of hydraulic servo manipulator show that the control strategy has better tracking performance and synchronous driving performance than the traditional PID control.

double hydraulic motors driving model; iterative learning control (ILC) algorithm;IL-PID synchronization control; electro-hydraulic servo driving

2013-12-09

TG156DOI：10.3969/j.issn.1004-132X.2015.04.008

劉湘琪，女，1975年生。浙江理工大學機械與自動控制學院博士研究生,杭州電子科技大學機械工程學院講師。主要研究方向為機械設計及理論。發表論文7余篇。蒙臻，男，1986年生。浙江理工大學機械與自動控制學院博士研究生。倪敬，男，1979年生。杭州電子科技大學機械工程學院教授、博士。朱澤飛(通信作者)，男，1963年生。杭州電子科技大學黨校辦教授、博士研究生導師。