蜂窩復合材料超聲輔助切割工具設計

吳　欣　胡小平　于保華　紀華偉　陸志平　夏曉晴

杭州電子科技大學,杭州,310018

蜂窩復合材料超聲輔助切割工具設計

吳欣胡小平于保華紀華偉陸志平夏曉晴

杭州電子科技大學,杭州,310018

在蜂窩復合材料超聲輔助切割系統設計中，針對大變幅系數超聲變幅桿的設計及其與加工工具配合的問題，基于“代替法”，結合有限元評估技術，建立了超聲變幅桿和加工刀具的連接結構設計方法。首先，基于超聲輔助加工原理，設計了具有大變幅能力的階梯-懸鏈型復合變幅桿。然后，基于“代替法”，研究變幅桿長度減小對變幅桿聲學性能的影響規律。進而，基于有限元仿真技術，研究裝配后聲學系統的聲學性能。最后，采用設計的超聲輔助切割系統對蜂窩材料進行切割加工實驗研究，發現切割面無毛刺，加工過程無粉塵產生，從而驗證了設計的超聲輔助切割聲學系統的有效性。

超聲輔助;蜂窩材料;變幅桿;代替法

0　引言

蜂窩復合材料由于具有良好的比強度、比剛度、抗疲勞性能，在航空領域得到了廣泛應用。但在蜂窩材料的切割加工過程中,存在加工粉塵大，加工零件表面質量差、尺寸精度低的問題。超聲輔助加工工藝是指在蜂窩切割過程中給切割刀具施加耦合超聲振動，使刀具與工件材料之間發生間斷性沖擊與分離，最終使材料發生分離。超聲輔助切割工藝可以有效地避免加工粉塵的產生，并且獲取高質量的加工表面。

在復合材料超聲輔助加工方面，歐洲和美國的各大飛機制造廠和航空復合材料的研發生產企業已將超聲切割設備應用于生產。但是，由于國外公司的技術壟斷，故針對蜂窩材料的超聲輔助切割系統的相關資料極少公開。在國內,雖然對CFRP復合材料[1]、SiCp/Al復合材料等的超聲輔助加工工藝進行了一定的研究,但是關于蜂窩復合材料的超聲輔助加工的研究較為少見。

蜂窩復合材料切割系統不同于一般的超聲輔助加工系統,它需要具備較大的變幅能力，以實現蜂窩復合材料沖擊分離的目的。蜂窩復合材料超聲輔助切割時，為保證零件加工的質量和效率，工具端部的振幅需要達到20～30 μm,而一般的超聲換能器輸出振幅為2～3 μm,因此,需要采用具有較大變幅能力的變幅桿以獲取滿足工程需要的工具振幅。蜂窩復合材料的切割刀具為非規則形狀，其結構尺寸和質量相對于變幅桿而言較大,不能簡單地簡化為一個質量點進行處理，因而，不能簡單地以等效質量方法進行變幅桿的設計。切割刀具和變幅桿耦合在一起實現超聲系統的機械振動模式和振幅的放大。常規的基于一維波動方程的變幅桿設計方法不能為三維放大結構的設計提供有力的技術支撐。本文結合理論設計方法和有限元分析技術,對大變幅系數超聲變幅桿及其與工具的連接部分的設計問題進行了研究。

變幅桿的研究主要集中在常規的變幅桿如高斯型、懸鏈型和階梯型變幅桿,其中階梯型變幅桿具有加工方便、變幅能力強的特點，但同時截面變化部位的應力集中現象也比較明顯[2]。此外,隨著仿真技術和優化技術的發展,學者們也提出了一些新型的變幅桿。Wang等[3]基于遺傳算法,設計了Bazier曲線形狀的變幅桿,在實現較大變幅的同時也改善了變幅桿內部的應力分布狀況。Roopa等[4]在塑料連接工藝中研究了該變幅桿，得到了較好的結果。另外一種實現較大放大系數的變幅桿是復合變幅桿[5]。

變幅桿和工具耦合在一起時,傳統的設計方法往往基于等效質量法,如高斯變幅桿設計時,端部可以采用規則的圓柱進行替代[2]。但是該方法主要是針對工具的質量和尺度都比較小的情況，當工具的尺度比較大時，往往會產生較大的誤差。而有限元方法適應性廣，具有很強的靈活性，在超聲系統性能評估和設計方面應用廣泛[6-8]。

因此,本文基于“代替法”，結合有限元評估技術，研究了超聲變幅桿和加工刀具的連接結構設計方法及其關鍵技術。

1　階梯-懸鏈復合變幅桿設計

縱波在桿件中傳播的波動方程為

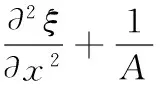
(1)

式中,w為圓頻率；E為彈性模量;ρ為密度;A為面積;ξ為質點位移。

本文設計的變幅桿分為兩段,上半段為λ/4的階梯型變幅桿,下半段為λ/4的懸鏈型變幅桿,λ為波長，如圖1所示。

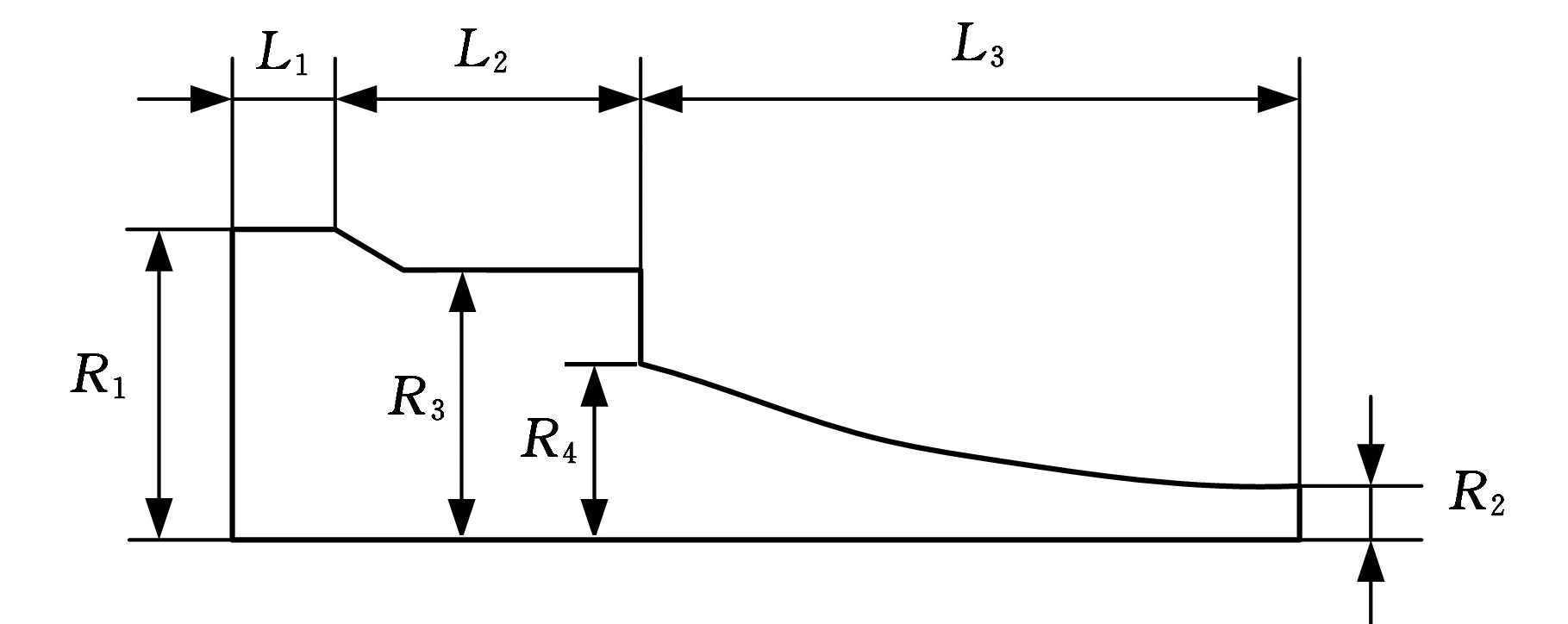
圖1　階梯-懸鏈復合變幅桿

節點在窄端的四分之一波長的階梯型變幅桿的頻率公式為

cot(kL1)cot(kL2)=S1/S2

(2)

式中,L1、L2分別為四分之一波長變幅桿的大端和小端的長度;S1、S2分別為大端和小端的面積。

根據式(2),選用L1為15 mm,L2為43.6 mm,大端半徑為43.5 mm,小端半徑為38 mm。

兩端自由的四分之一波長懸鏈型變幅桿長度為

(3)

根據式(3),設置懸鏈的大端半徑為25.5 mm,小端半徑為8 mm,計算懸鏈型變幅桿的長度為94.8 mm。

階梯-懸鏈復合變幅桿的相關參數如表1所示。為了與常規變幅桿的性能進行對比,設計了單一懸鏈型變幅桿，相關參數如表1所示。

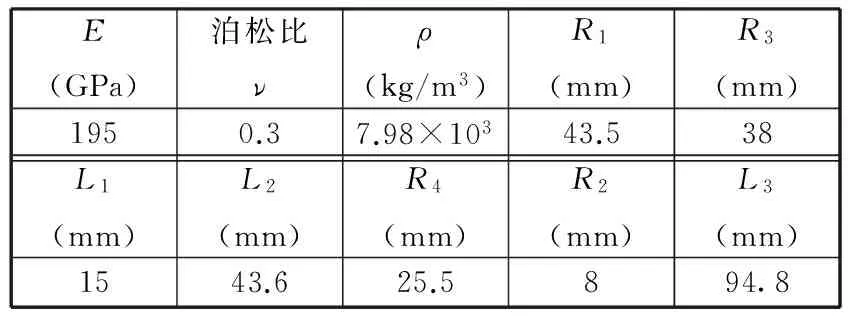
表1　階梯-懸鏈復合變幅桿結構參數

2　基于“代替法”的變幅桿與加工工具耦合設計

蜂窩材料切割刀具為一個非規則結構的刀片,如圖2所示。當超聲變幅桿耦合了切割刀具后,整個系統的縱振頻率、節點和放大系數會發生變化。因此,本文采用“代替法”設計變幅桿與工具的連接，即在變幅桿的端部截去一部分，取而代之的是加工工具，如圖3所示。由于切割刀具形狀復雜，采用理論分析較為困難，因此，結合有限元分析技術,動態調整分析模型的幾何尺寸,系統分析耦合后的聲學系統的性能。

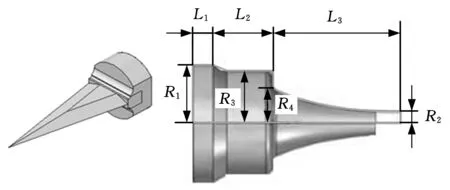
圖2　加工刀具圖3　代替法示意圖

2.1超聲輔助切割系統加工工具設計

超聲輔助切割系統加工工具由刀具和支座構成。刀具座具有支撐刀具和與變幅桿連接兩個功能，因此材料采用與變幅桿性能相差不大的鋼材。刀具選用硬質合金，硬質合金刀具的彈性模量和密度都比較大,在振動的過程中相當于一個質量塊，因此對刀具座與變幅桿的連接具有較高的要求。如果采用剛度和硬度都比較小的鈦合金,可能出現刀片橫向擺動,從而導致切割時刀具不鋒利的現象出現。

2.2變幅桿截去后的性能分析

首先分析變幅桿尺寸調整后的性能數據，即研究長度縮短后變幅桿的振動特性。采用FEMAP前處理軟件中的模型特征編輯命令可以方便地修改變幅桿的長度。通過NXNASTRAN分析，得到隨變幅桿的長度減小,變幅桿放大系數和縱振頻率的變化規律。

從圖4中可以看到,隨著四分之一波長的懸鏈變幅桿的長度減小,復合變幅桿的縱振頻率線性增加。從圖5中可以看出,變幅桿的放大系數隨其長度的減小而逐漸減小。在研究的范圍內，超聲變幅桿的聲學性能基本呈線性變化。

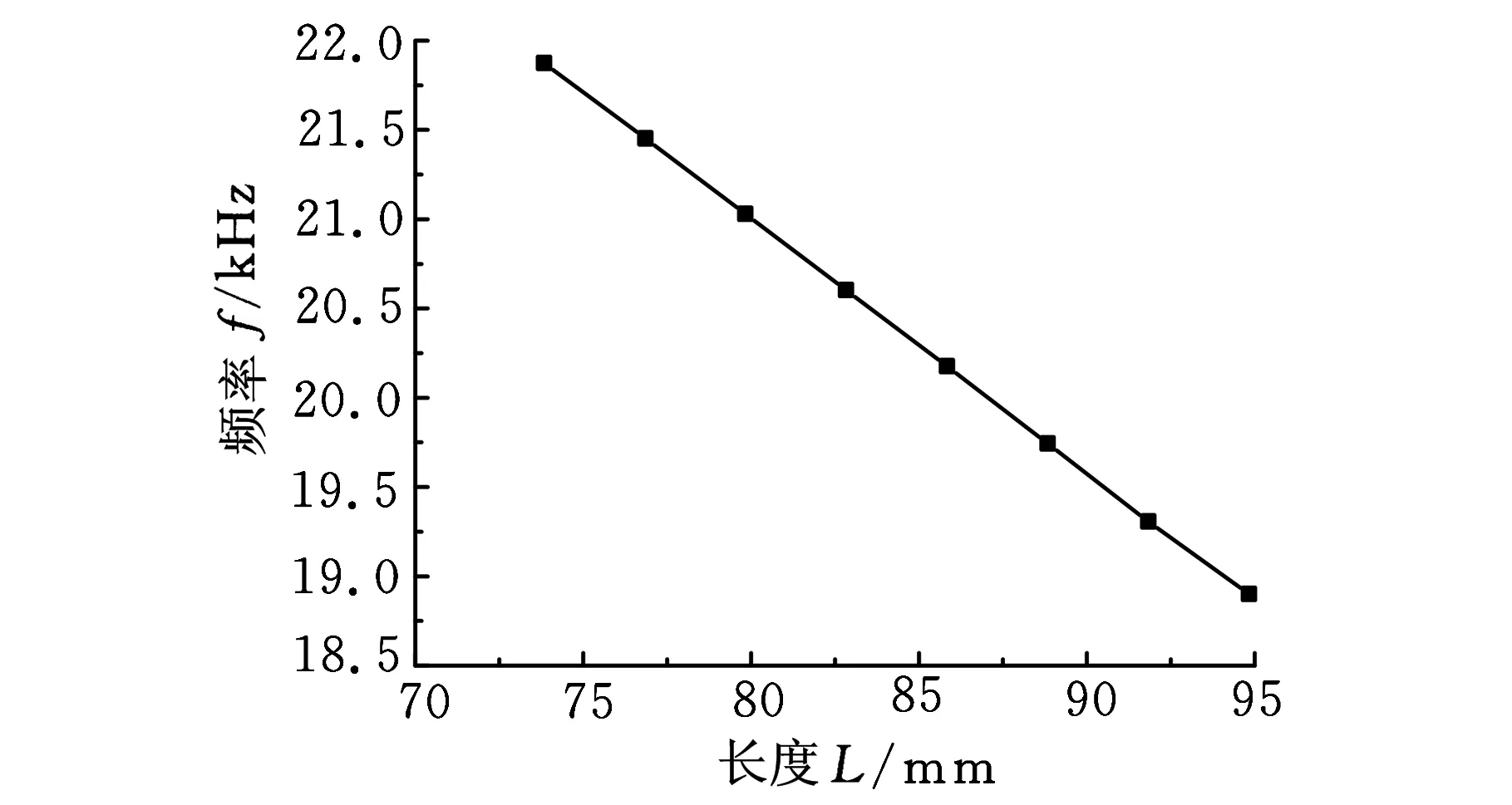
圖4　縱振頻率隨長度的變化規律

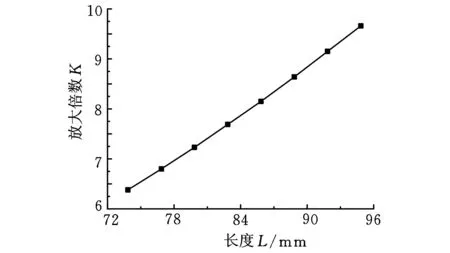
圖5　放大系數隨長度的變化規律

2.3整體聲學系統性能評估

刀具和變幅桿耦合在一起后，結構的性能將會發生顯著變化,因此,采用有限元技術虛擬評估耦合在一起的切割工具的振動特性。首先，將工具耦合到分析模型中，分析整體系統的動力學性能。然后通過調整變幅桿的長度得到整體的聲學系統性能。基于有限元分析結果，設計復合變幅桿中的懸鏈部分的桿件長度由94.84 mm減小為79.84 mm。

有限元分析結果表明，整體聲學系統的放大系數為9.765,比原先的復合變幅桿的放大系數9.66稍大。分析其原因,認為刀具為薄片狀,導致整體聲學系統的長度為180.6 mm,要大于初始設計的變幅桿的長度153.6 mm,所以刀尖的振幅有所增大。

基于有限元方法計算得到整體聲學系統的縱振頻率為19.74 kHz。超聲電源的工作頻率設計為20 kHz,模型的縱振頻率與設計頻率的相對誤差為1.3%,滿足設計要求。

圖6所示為超聲聲學系統19.74 kHz下的縱振模式。圖7給出了超聲聲學系統在19.74 kHz縱振模態下沿變幅桿軸線方向節點的相對位移。該節點位移不是變幅桿在激振下的真實振幅。但是根據模態計算原理，該位移為系統在諧振狀態下結構各點振幅相對于基準點變換后的相對位移,因此,該曲線可以認為是在19.74 kHz激振頻率下,結構沿變幅桿軸線方向振幅的相對變化規律。

圖6　超聲聲學系統19.74 kHz下的縱振模式

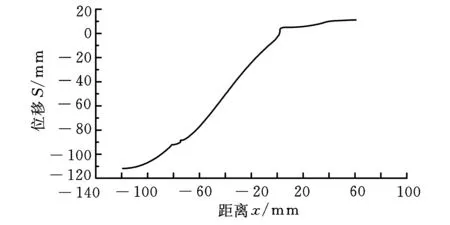
圖7　19.74 kHz縱振模式下沿變幅桿軸向上節點的位移曲線

變幅桿節點處的振幅為零。從圖7中可以看到：當x=1.5 mm時,計算得到的位移為0，該處即為仿真得到的節點。曲線中的橫坐標為變幅桿軸向方向，坐標為零(x=0)處是切割刀具結構設計的節點，該處計算得到的位移為-3 mm,該位移相對于端部120 mm的位移而言非常小。可見，設計的節點位置和計算得到的節點位置相差不超過1.5 mm。

此外，一般變幅桿的節點處需要加上一個支撐法蘭，該支撐法蘭厚度在理論上認為越薄越好，但是在工程應用中,一般為1～3 mm,以保證支撐法蘭的剛度，而設計的節點位置和仿真得到的節點位置偏差僅為1.5 mm,所以,可以認為設計的變幅桿節點位置與計算得到的節點位置基本吻合。

3　加工刀具幾何結構和材料參數對聲學系統穩健性的影響

超聲聲學系統的設計中可控因素為產品的幾何結構，不可控因素是材料的性能參數如材料的彈性模量和密度。因此，本文主要研究刀具的彈性模量發生的微小變動對結構的縱振的頻率、模式和放大系數的影響規律，即結構性能對材料彈性模量的敏感程度。

3.1變幅桿加工對稱性對超聲聲學系統性能的影響

當變幅桿加工精度較低時,如變幅桿結構的對稱性較差,結構振動時,薄片狀結構切割刀具會因彎曲剛度不足而發生擺動。該擺動現象會導致刀片切割材料時發生過度摩擦現象,嚴重時發生刀片斷裂現象。

為了表現變幅桿關于刀片中面的非對稱性,對變幅桿一側細分網格,另一半劃分粗糙網格。當模型網格對稱時(圖8a),刀具具有較好的縱振模式。而當變幅桿的對稱性較差時(圖8b),刀片具有明顯的彎曲模式。因此，加工變幅桿時需要注意其對稱性，以保證刀具的壽命。

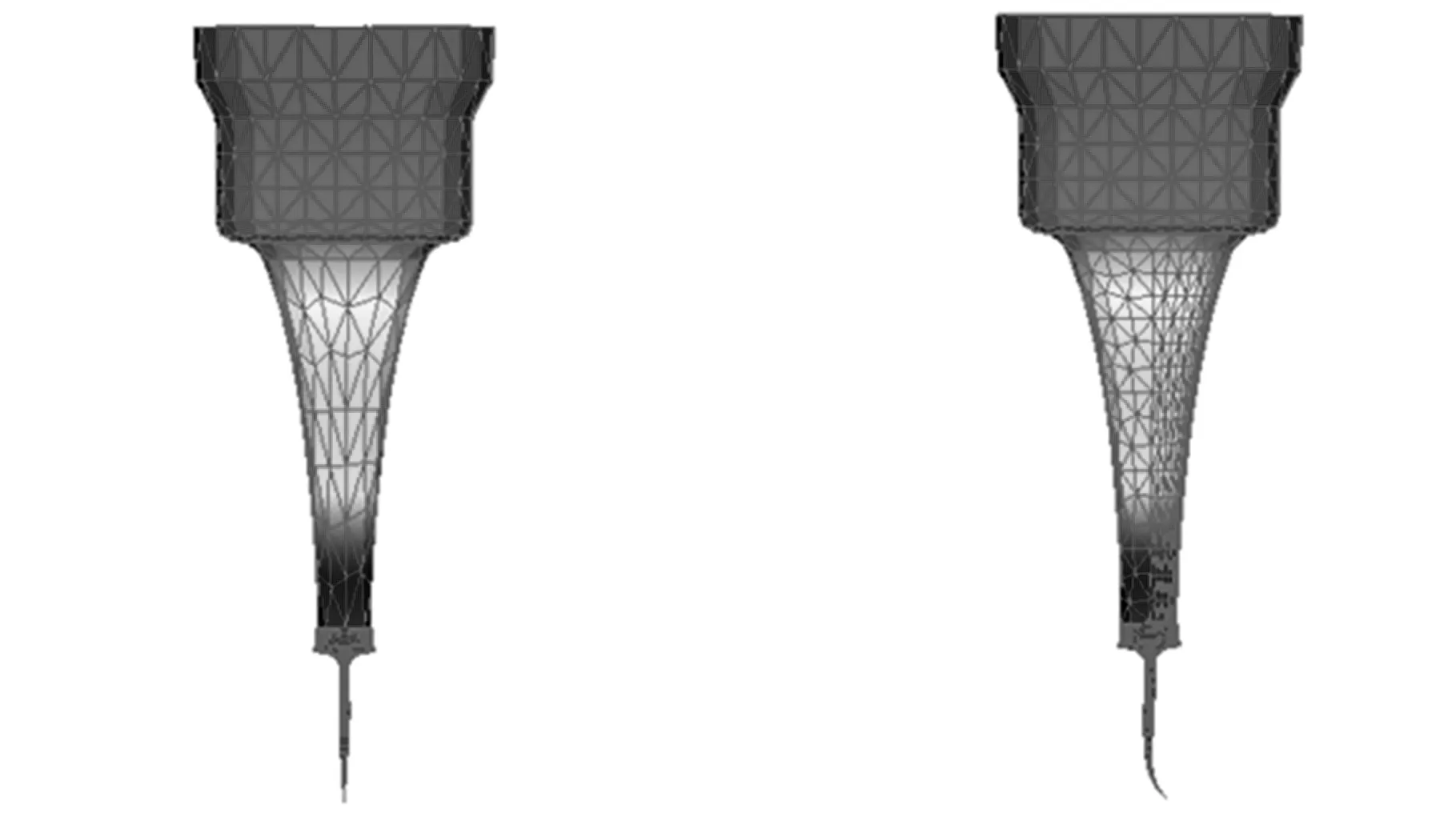
(a)對稱性較好(b)對稱性較差圖8　變幅桿對稱性對縱振模態的影響

3.2刀具材料性質波動對超聲聲學系統的影響

硬質合金多為鈷(Co)鎳(Ni)合金,不同的牌號材料性質相差較大。表2給出了刀具材料密度為14.81×103kg/m3,取不同的彈性模量值時，計算得到的變幅桿縱振頻率和放大系數。由表2可以發現當刀具的彈性模量發生變化時，聲學系統的縱振頻率基本不發生變化，而放大系數會有一定的變化。在研究的彈性模量取值范圍內，當彈性模量有10%的變化時，放大系數僅有1%的變化。所以,在彈性模量的取值范圍內,可以認為刀具彈性模量的變化對聲學系統的影響較小。

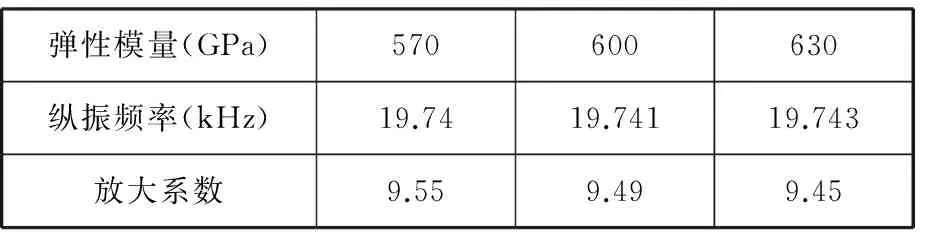
表2　刀具不同彈性模量時的聲學系統縱振頻率

4　超聲輔助切割過程實驗研究

4.1超聲輔助切割系統縱振頻率測試

為了使變幅桿能夠固定在工作臺架上,在變幅桿節點處增加了支撐結構，進而采用數控加工的方式，加工出設計的蜂窩復合材料切割系統,如圖9所示。

圖9　超聲輔助切割聲學系統

對加工的超聲輔助切割系統進行相關數據的采集。利用型號為TH2818的同惠元件分析儀測試變幅桿和裝配好的切割工具的聲學系統的縱振頻率，測試結果如圖10所示。

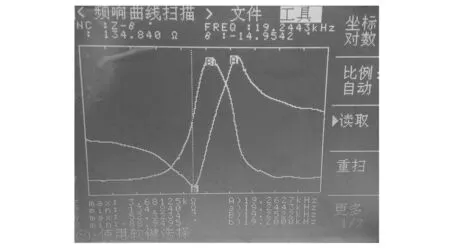
(a)變幅桿縱振頻率

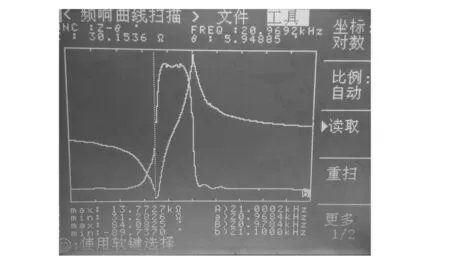
(b)聲學系統縱振頻率圖10　變幅桿和整個聲學系統縱振頻率測試

變幅桿的縱振頻率和耦合加工刀具之后的縱振頻率分別為20.97 kHz和19.24 kHz,而采用有限元設計計算的頻率分別為21.4 kHz和19.74 kHz,兩者相對于實驗測試數據的相對誤差分別為1.9%和2.6%。誤差產生的原因為：一方面可能是加工變幅桿的曲線形狀具有一定偏差，另一方面取用的材料參數可能有所偏差。

4.2蜂窩復合材料切割實驗

采用設計的超聲輔助切割平臺對蜂窩復合材料進行切割實驗。

超聲輔助加工過程中,換能器輸入功率為0.12kW,工作頻率為19.2kHz。刀尖部位的振幅難以測量，因此，對變幅桿端部的振幅進行了測量，變幅桿端部振幅為17 μm。切割時，將蜂窩材料粘到工作臺上，工作臺采用伺服驅動進給,實驗裝置如圖11a所示。

切割后的蜂窩復合材料表面如圖11b所示。蜂窩材料的切割過程是一個粗加工過程，對加工零件的表面加工精度沒有細致要求,僅要求加工表面沒有明顯毛刺。而從圖11b中可見,蜂窩復合材料的切割平面光滑,沒有明顯毛刺產生,滿足蜂窩復合零件加工要求。

(a)加工過程(b)加工表面圖11　切割蜂窩復合材料實驗

此外,當不耦合超聲振動進行切割時，由于需要的切割力較大，材料較為難以切割，并且切割過程中會有粉塵產生。因此，設計的超聲輔助切割系統不僅可以有效地減少加工過程產生的粉塵,而且可以大幅減小加工過程中的材料切割力。

在材料切割過程中存在變幅桿溫升較高的現象,這意味著變幅桿和切割刀具之間存在著一定的阻抗匹配問題，這也是下一步研究的重點問題。

5　結論

本文針對蜂窩復合材料的加工過程，基于超聲輔助加工原理，設計了超聲輔助加工聲學系統。針對大變幅系數超聲變幅桿與加工工具配合的問題，基于“代替法”，結合有限元評估技術，建立了超聲變幅桿和加工刀具的連接結構設計方法。采用設計的超聲輔助切割系統對于蜂窩材料進行切割加工實驗研究，研究過程表明：

(1)階梯-懸鏈復合變幅桿具有10倍振幅放大能力，而同樣截面尺寸的懸鏈變幅桿的放大系數為4.9。

(2)提出了基于代替法和有限元評估技術的變幅桿和工具耦合設計方法，設計了滿足要求的超聲輔助切割系統。

(3)蜂窩復合材料切割實驗研究表明,超聲輔助切割工藝可以實現快速高質量的蜂窩復合材料切割，并且加工過程無粉塵產生。

(4)在蜂窩復合材料切割實驗中發現超聲變幅桿部位存在較大溫升現象，該問題是下一步研究重點。

[1]馬付建. 超聲輔助加工系統研發及其在復合材料加工中的應用[D]. 大連: 大連理工大學, 2013.

[2]林仲茂.超聲變幅桿的原理和設計[M]. 北京: 科學出版社, 1987.

[3]Wang D A,Nguyen H D.A Planar Bezier Profiled Horn for Reducing Penetration Force in Ultrasonic Cutting [J]. Ultrasonics, 2014, 54(1): 375-384.

[4]Roopa Rani M, Rudramoorthy R. Computational Modeling and Experimental Studies of the Dynamic Performance of Ultrasonic Horn Profiles Used in Palstic Welding[J]. Ultrasonic,2013,53(3):763-772.

[5]張可昕. 基于有限元的超聲復合變幅桿的動力學分析及優化設計[D]. 北京：北方工業大學, 2012.

[6]Lucas M,MacBeath A,McCulloch E,et al.A Finite Elment Model for Ultrsonic Cutting[J].Ultrasoincs, 2006, 44: 503-509.

[7]Kuo K L. Ultrasonic Vibrating System Design and Tool Analysis[J]. Transactions of Nonferrous Metals Society of China, 2009,19(S1): 225-231.

[8]馮冬菊,趙福令,徐占國.使用Inventor軟件的超聲變幅桿模態分析[J].應用聲學,2010,29(1):69-73.

Feng Dongju,Zhao Fuling,Xu Zhanguo.Modal Analysis of Ultrasonic Horn Using theInventor Software[J].Applied Acoustics,2010,29(1):69-73.

(編輯袁興玲)

Design of Ultrasonic Cutting Tool for an Ultrasonic Assisted Cutting Process of Nomex Honey-comb Materials Based on Substitution Method

Wu XinHu XiaopingYu BaohuaJi HuaweiLu ZhipingXia Xiaoqing

Hangzhou Dianzi University,Hangzhou,310018

A substitution method under help of the finite element method was proposed to solve the problem of the coupled design of a composite horn and the cutting tool of an ultrasonic acoustic system for the noomex honeycomb material cutting process.First,a stepped-catenoidal composite horn with high displacement amplification factor was designed by using the theory of elastic wave propagation and finite element analysis technique.Then,the influences of the horn length on the vibration characteristics were studied based on substitution method using finite element method.The performance of the ultrasonic vibration system was studied by using finite element method.Finally,the ultrasonic acoustic system was fabricated and the ultrasonic assisted cutting experiments were performed,and the nomex honeycomb materials were cut effectively by using the designed system.The machined surface shows high surface quality which is smooth without burrs.Thus,the effectiveness of the designed cutting tools was demonstrated.

ultrasonic;nomex;horn;substitution method

2014-03-17

國家自然科學基金資助項目(KYZ013710037);中國博士后科學基金資助項目(2013M541769)；國防科工局重大專項(A3920133001)；浙江省自然科學基金資助項目(LY14E050025)

TH136DOI：10.3969/j.issn.1004-132X.2015.06.019

吳欣，男，1979年生。杭州電子科技大學機械工程學院講師、博士。主要研究方向為材料成形過程仿真技術。發表論文10余篇。胡小平，女，1971年生。杭州電子科技大學機械工程學院教授。于保華，男，1978年生。杭州電子科技大學機械工程學院工程師、博士。紀華偉，男，1976年生。杭州電子科技大學機械工程學院副教授、博士。陸志平，男，1974年生。杭州電子科技大學機械工程學院高級工程師。夏曉晴，女，1989年生。杭州電子科技大學機械工程學院碩士研究生。