一種半波整流的非對稱結構LLC諧振變換器

廖鴻飛，熊 宇，王志強

（1.中山火炬職業技術學院 電子工程系，中山 528436；2.華南理工大學 電力學院，廣州 510641）

0 引言

由于LLC諧振變換器的功率器件能在全負載范圍內實現軟開關，因此在大功率場合得到了廣泛的應用。但是橋式LLC諧振變換器的輸出通常采用全波整流，其功率器件數量較多，變壓器副邊需要中心抽頭，繞制復雜，成本較高，使LLC諧振變換器在小功率場合中應用較少。

相對于全波整流，半波整流的器件數量最少，并且變壓器不需要中心抽頭，結構簡單，可以有效的降低成本。采用半波整流的LLC諧振變換器，由于其原邊諧振網絡在一個開關周期中的諧振是非對稱的，因此稱為非對稱結構LLC諧振變換器[1]。而全波整流的LLC諧振變換器稱為對稱結構LLC諧振變換器。

本文對非對稱結構LLC諧振變換器的工作原理和參數設計進行了詳細分析，并設計了120W的實驗樣機，對非對稱結構LLC諧振變換器的參數設計及性能進行了驗證。

1 非對稱結構LLC諧振變換器的工作原理分析

非對稱結構LLC諧振變換器的結構圖如圖1所示，該圖中Vin為輸入直流電壓；開關管Q1和Q2為變換器中半橋結構的兩個開關管，Q1，Q2互補導通，其占空比固定為50%。DS1和DS2分別為開關管Q1和Q2的體二極管；CS1和CS2為開關管Q1和Q2的寄生電容；Cr為串聯諧振電容；Lm為勵磁電感，Lr為串聯諧振電感，變壓器的變比為n；D為副邊整流二極管，C為輸出濾波電容，RL為負載。

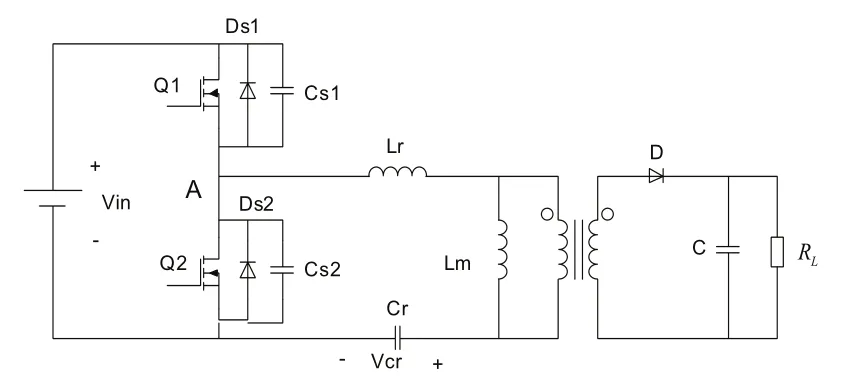
圖1 非對稱結構LLC諧振變換器示意圖

非對稱結構LLC諧振變換器的工作波形如圖2所示，在一個開關周期中，非對稱結構LLC諧振變換器有7個工作階段。

階段1（t0-t1），當t=t0時，變換器上管Q1導通，Q2斷開，Q2的漏源極之間的電壓為Vin；原邊串聯諧振電感Lr與電容Cr諧振，輸出整流二極管正向導通，輸入電源的能量通過變壓器和輸出整流二極管向輸出傳遞。同時變壓器的原邊被輸出電壓箝位，變壓器原邊電壓為Vp=nVo，激磁電感電流在原邊電壓作用下線性上升。

階段2（t1-t2），當t=t1時，激磁電感的電流與諧振電流相等，輸出整流二極管的電流下降到零，自然關斷，原邊激磁電感Lm不再被箝位，與諧振電感Lr，諧振電容Cr構成串聯諧振。由于這個諧振比前一個諧振的周期大很多，因此電流近似為線性。

階段3（t2-t3），當t=t2時，Q1關斷，為防止Q1，Q2同時導通，Q1關斷后，在Q2導通前有一定的死區時間，此時Q1，Q2均為關斷狀態。由于此時原邊諧振電流正向流動，諧振電流給Q2的寄生電容Cs2放電，并給Q1的寄生電容Cs1充電，Q2的漏源極之間的電壓下降至零。

階段4（t3-t4），當t=t3時，由于Q2的漏源極之間的電壓下降到零，Q2的體二極管DS2導通，原邊電流通過Q2的體二極管繼續流動，并反向增大。DS2的導通，為Q2的零電壓開通創造了條件。當t=t4時，給Q2的柵極施加一個高電平，Q2實現零電壓開通。

階段5（t4-t5），當t=t4時，Q2導通，而D一直處于截止狀態，因此原邊激磁電感Lm, 串聯諧振電感Lr和諧振電容Cr構成諧振。由于Lm較大，因此此諧振周期較長，其諧振頻率遠小于開關頻率，諧振網絡的電壓超前于電流。經一段時間后，諧振電流將反向流動。

階段6（t5-t6）當 t=t5時，Q2關斷，在死區時間內，原邊的諧振電流將給Q1和Q2的寄生電容充電，使A點電位上升到Vin，此時Q1的漏源極之間的電壓下降到零。

階段7（t6-t7）當t=t6時，由于Q1的漏源極之間的電壓下降到零，Q1的體二極管DS1導通。當t=t7時，給Q1的柵極施加一個高電平，Q1實現零電壓開通。

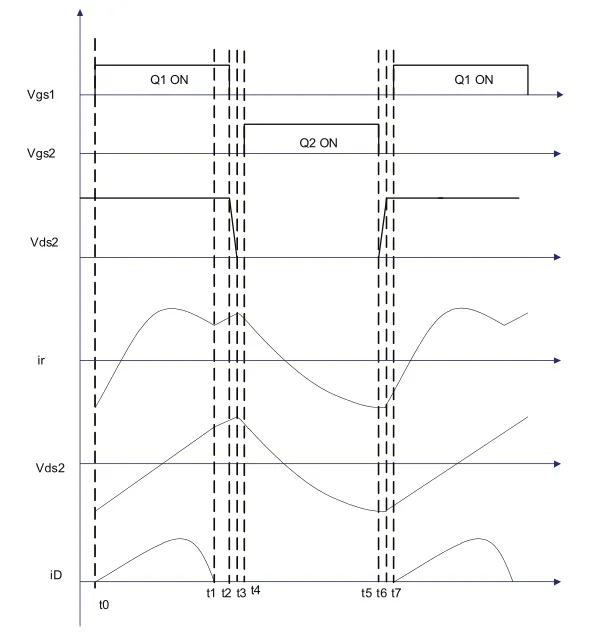
圖2 非對稱結構LLC諧振變換器的工作波形

2 參數設計

2.1 輸出負載特性

由于諧振變換器的特性對負載存在一定的依賴性，因此在對LLC諧振變換器進行參數設計時，需要對副邊整流電路進行等效分析，獲得其交流等效電阻。由于非對稱結構LLC諧振變換器的輸出采用半波整流，輸出整流二極管只在半個周期內導通，因此與傳統的LLC諧振變換器的交流等效負載不同。

LLC諧振變換器的變壓器輸出為電流源性質，其電流波形近似為正弦波。輸出電流平均值IO與整流網絡輸入電流有效值Iinrms之間的關系為：

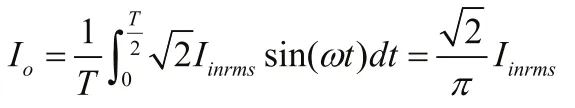
假設此整流二端網絡的輸入電阻為Ri，忽略二極管的損耗，由功率平衡：

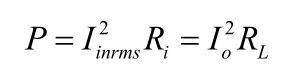
折算到變壓器原邊可以得到等效交流電阻為：

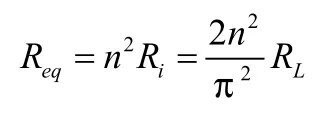
從上式可以看出，在相同負載情況下，半波整流電路的等效電阻小于全波整流電路的等效電阻[2]。

2.2 增益特性分析

由變換器的工作原理分析得到，變換器在Q1導通期間向負載傳遞能量，Q2導通期間原邊諧振主要是為了使Q1實現軟開關。因此在Q1導通期間，諧振網絡的等效模型如圖3所示。VinFHA為開關網絡提供的方波的基波分量，Vp為輸出電壓通過變壓器折射到原邊的電壓。

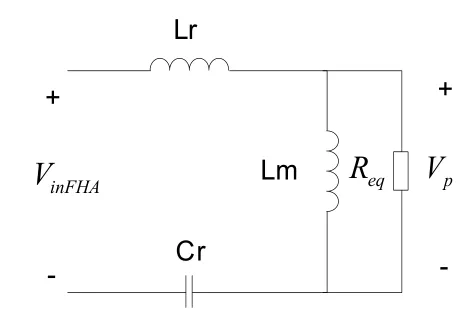
圖3 諧振網絡的等效模型

諧振網絡的交流增益為[3]：

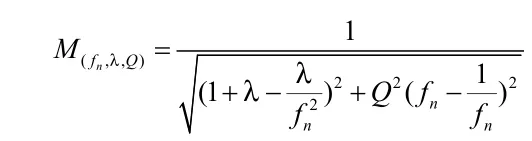
從以上分析可以看出，非對稱結構LLC諧振變換器在向負載輸出能量時發生諧振，其諧振特性與對稱結構的LLC諧振變換器非常接近。但是由于半波整流的負載交流等效電阻小于全波整流的交流等效電阻，因此在相同參數條件下，非對稱結構的LLC的Q值大于對稱結構的LLC的Q值，非對稱結構LLC的曲線更為平緩，這意味著在負載發生變化時，工作頻率的變化范圍相對較寬。圖4所示為相同參數條件下非對稱結構與對稱結構LLC諧振變換器的增益曲線對比。

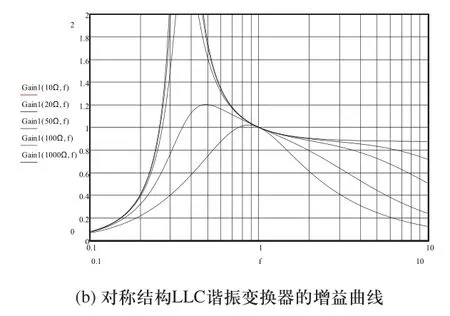
圖4 兩種結構LLC諧振變換器的增益曲線

2.3 軟開關條件分析

LLC諧振變換器實現ZVS的條件，是諧振網絡工作在感性區域，電壓超前于電流。由于非對稱結構LLC在不同開關模態下，諧振網絡的結構不同，因此有必要對其ZVS條件進行分析。

當Q1導通、Q2關斷時，其諧振網絡的輸入阻抗為：

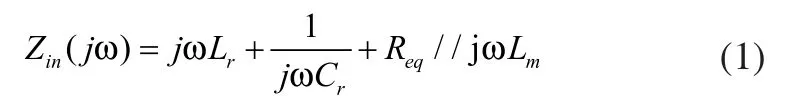
當Q1關斷、Q2導通時，其諧振網絡的輸入阻抗為：

要使諧振網絡工作于感性區域，需要兩種狀態下的阻抗角均大于零。因此可得到實現ZVS的最大Q值為，其中Mmax為所需的最大交流增益。

同時，從原理分析中可知，在死區時間內，激磁電流需要給寄生電容放電，使MOSFET實現ZVS，因此有：

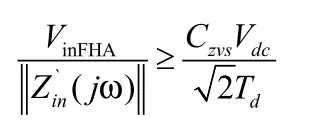
因此可得：

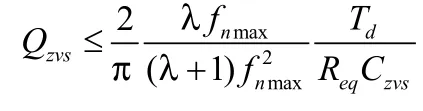
式中，fnmax為最高歸一化頻率，Td為死區時間，Czvs為MOSFET的寄生結電容。

設計時，為了保證實現軟開關，所取Q值應小于Qmax以及Qzvs。

2.4 電流應力分析

對于非對稱結構的LLC諧振變換器，輸出整流二極管只在Q1導通的半個周期內導通，進行能量傳遞，原副邊電流應力均大于對稱結構的LLC諧振變換器。在Q1導通期間，原邊電流包含輸出的電流及激磁電流，其有效值為[4]：

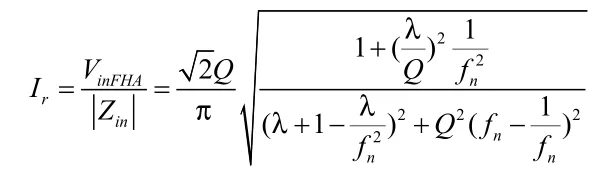
由式(1)可見，非對稱結構LLC變換器的輸入阻抗與對稱結構LLC變換器基本接近，因此兩種結構的LLC變換器原邊電流也基本接近。

輸出整流二極管電流為原邊諧振電流與激磁電流之差，而原邊諧振電流ir(t)與原邊激磁電流im(t)為：

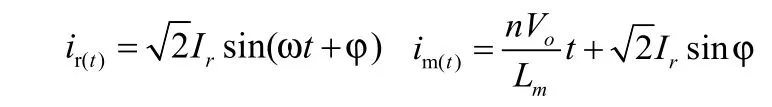
因此輸出整流二極管電流為：

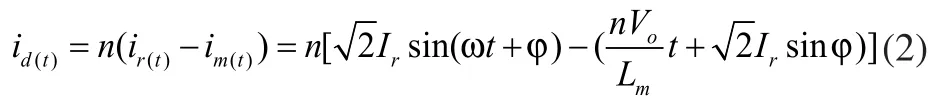
其中ω為諧振角頻率，φ為諧振網絡電壓與電流的相位差。

從式(2)可以看到，輸出整流二極管電流并非純正弦波，其平均電流為負載電流，因此輸出整流二極管的峰值電流大小取決于其導通時間的長短，而輸出整流二極管的導通時間為原邊諧振電流和勵磁電流相等的時刻。與相同負載下的對稱結構LLC諧振變換器相比較，由于非對稱結構LLC諧振變換器原邊諧振電流增大，而原邊激磁電流的斜率相同，因此非對稱結構LLC諧振變換器輸出整流二極管的導通時間增長，其峰值電流得到有效控制。圖5為兩種結構LLC諧振變換器的仿真波形圖，從仿真波形中可見，非對稱結構LLC諧振變換器的輸出整流二極管的峰值電流為對稱結構LLC諧振變換器輸出整流二極管峰值電流的1.6倍。

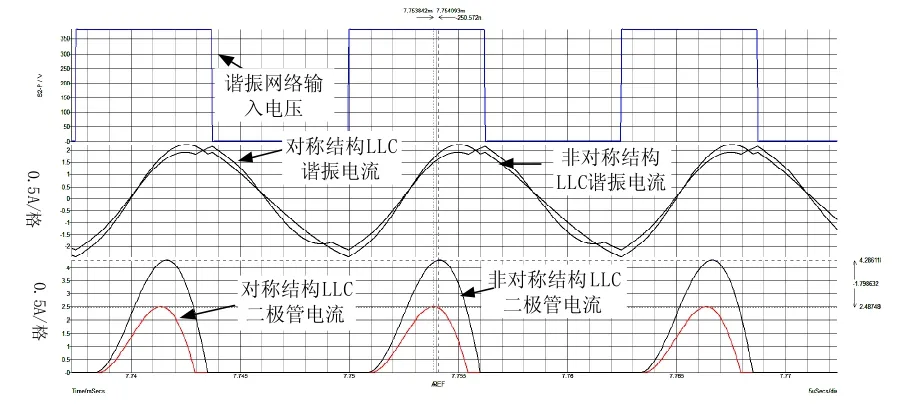
圖5 對稱結構LLC諧振變換器與非對稱結構LLC諧振變換器仿真波形對比

3 實驗驗證

為驗證該方案的可行性，根據上述的參數設計方法，設計了120W的驗證電路，輸入電壓為Vin=390Vdc，輸出電壓為Vo=24V，輸出電流為Io=5A， Lr=105μ H，Lm=750μ H，Cr=22nF，變壓器采用PQ32/30磁芯，采用L6599為控制芯片。

圖6為Q2的驅動波形Vgs及漏源極之間的波形Vds，Q1,Q2之間留有一定的死區時間。從波形中可見，Q2導通前，其DS電壓已經下降到零，Q1，Q2均實現了ZVS。圖7為輸出整流二極管電流id與電壓波形Vd，從圖中可見，輸出整流二極管關斷前電流已經下降到零，輸出整流二極管實現了ZCS。

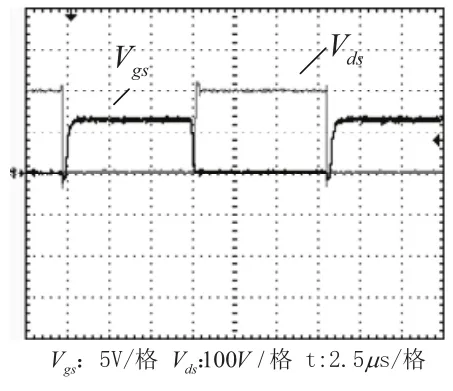
圖6 Q2驅動波形及DS波形

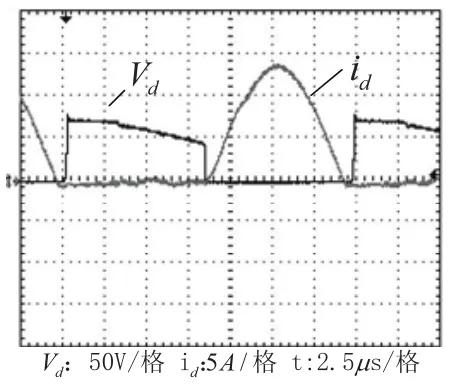
圖7 輸出整流二極管電壓與電流波形

4 結論

針對全波整流的LLC諧振變換器輸出整流功率器件較多，變壓器結構復雜等缺點，本文對采用半波整流的非對稱結構LLC諧振變換器進行了研究，分析了其工作原理和參數設計方法，仿真研究和實驗數據表明，該方案是切實可行的，非對稱結構LLC諧振變換器所有器件均能實現軟開關，結構簡單。該方案的提出，對LLC諧振變換器在小功率場合的應用具有重要意義。

[1] 顧亦磊,等.非對稱結構多路輸出LLC諧振型變換器[J].中國電機工程學報,2006,26(5):82-87.

[2] R.L.Steigerwald,A Comparison of Half-Bridge Resonant Converter[J].IEEE Transaction on power electronics 1988,3(2):174-182.

[3] James F L,Robert M.Steady-state analysis of the LLC series resonant converter[A].Proceedings of Annual Applied Power Electronics Conference,California[C],US,2001.

[4] 馬皓,等.一種改進的LLC變換器諧振網絡參數設計方法[J].中國電機工程學報,2008,28(23):6-11.

[5] Junseok Cho,Joonggi Kwon, Sangyoung Han.Asymmetrical ZVS PWM Flyback Converter with Synchronous Recti fi cation for Ink-Jet Printer[J].Power Electronics Specialists Conference[C].2006,1-7 .

[6] 李偉平,等.基于LLC的計算機電源設計[J].電力電子技術,2014.48(11):31-33.