利用面積法求有關線段的長
☉江蘇省泰州市第二中學附屬初中曹文喜 汪 艷
利用面積法求有關線段的長
☉江蘇省泰州市第二中學附屬初中曹文喜汪艷
面積法就是通過面積的相互轉化或面積與邊、角關系的互相轉化,而使問題得到解決的方法.對三角形而言,就是指利用三角形的面積自身相等的性質,或根據等高(底)的兩個三角形的面積之比等于對應底邊(對應高)的比的性質等進行解題的一種方法.利用面積法解題具有便捷、快速的特點,它是中學數學中一種常見的解題方法.現舉例如下.
一、利用三角形的面積自身相等的性質求線段的長
問題1:已知等腰△ABC中,AB=AC=10,底邊BC上的高AD=8,求腰AC上的高BE的長.
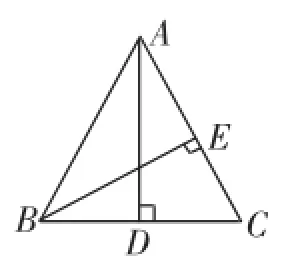
圖1
分析:如圖1,由勾股定理可得DC= 6,根據等腰三角形的“三線合一”的性質得到BC=12,利用△ABC自身的面積相等的性質得:BC·AD=AC·BE,這樣很快就求得BE=9.6.
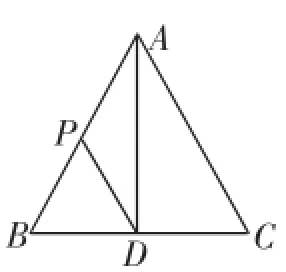
圖2
變式1:如圖2,已知△ABC中,AD是△ABC的中線,AD=4,BC=6,AC=5,點P是AB邊上的一點,且△PBD是以BP為底的等腰三角形,求線段AP的長.
分析:過D作DH⊥AB,垂足為H,因為AC2=AD2+CD2,所以∠ADC=90°,即AD⊥BC.
根據等腰三角形的“三線合一”的性質,得到PH= HB,所以PB=,所以線段AP的長為.
總結:運用面積法,需要借助等腰三角形的“三線合一”的性質和勾股定理,這樣才能利用三角形的面積自身相等的性質求出有關線段的長.
變式2:如圖3,在△ABC中,AD⊥BC于D,CE⊥AB于E,CE與AD交于H,已知EH=EB=3,AE=4,求AD的長.
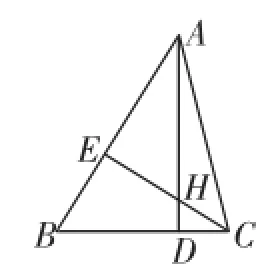
圖3
在Rt△AEH和Rt△CEB中,因為EH=EB,所以可證得Rt△AEH≌Rt△CEB,所以CE=AE=4,CB=AH=5.
總結:運用面積法,需要利用三角形全等求出有關線段的長,這樣才能很便利地利用三角形的面積自身相等的性質解題.
變式3:如圖4,已知在△ABC中,BC=10,底邊BC上的高為AD,∠A=45°,AD⊥BC,垂足為D,且BD=6,BE⊥AC,垂足為E,BE交AD于O,求O點到AB的距離.
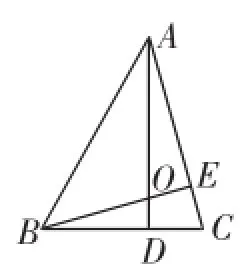
圖4
分析:這是一道難度較大的綜合題,過O作OH⊥AB,垂足為H,則OH的長就是O點到AB的距離.根據三角形的面積自身相等的性質,如果我們能夠求出AO、AB的長,那么我們就可以求出OH的長.因為∠A=45°,BE⊥AC,所以AE=BE.易得△AOE≌△BCE,所以OA=BC=10.
總結:運用面積法,需要根據題目所給的特殊條件,運用相似三角形和全等三角形的性質,這樣才能利用面積法求出有關線段的長.
拓展1:求證矩形一邊上的任意一點到兩對角線的距離之和為定值.
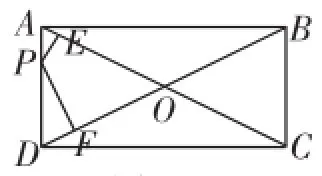
圖5
如圖5,矩形ABCD中,AB=m,BC=n,P為AD邊上的任意一點,PE⊥AC,PF⊥BD,求證:PE+PF的長為定值.
分析:在矩形ABCD中由AB=m,BC=n,可得對角線AC=BD=,連接OP,則可把△AOD拆分成△AOP和△ODP,這樣△AOD的面積就等于△AOP的面積和△ODP的面積的和,作OH⊥AD,根據△AOD自身的面積相等的性質可得:AD·OH,所以PE+PF=即PE+PF的長為定值.
總結:這是一道以矩形為背景的題,其本質也是利用三角形自身的面積相等的性質解題,只是將三角形拆成便于求解面積的兩個小三角形而已.
拓展2:如圖6,在平面直角坐標系中,四邊形OABC為矩形,OC=6,OA=8,將矩形OABC沿AC翻折,點B正好落在點D處,求D點的縱坐標.
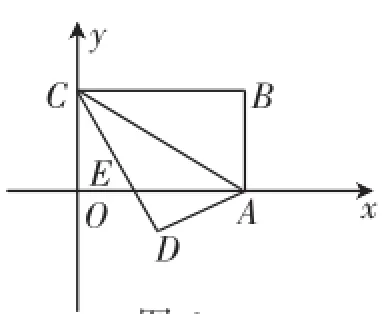
圖6
分析:過點D作DH⊥x軸,垂足為H.設OE的長為x,則AE的長為(8-x).
由題意可知∠BCA=∠ACD,∠BCA=∠OAC,所以∠ACD=∠OAC,所以EC=EA=8-x.
在△OEC中,(8-x)2=62+x2,解得x=.
總結:這是一道將矩形置于平面直角坐標系中的問題,可以先根據勾股定理和全等三角形的性質求出有關線段的長,再利用三角形的面積相等得到所要求的解.
拓展3:如圖7,四邊形ABCD是菱形,連接對角線AC,過點D作DH⊥AB于H,交AC于點M,CD=,對角線AC=10,求DH和MB的長.
分析:連接BD交AC于O,因為四邊形ABCD是菱形,所以AC⊥BD,且AC、BD互相垂直平分,所以AO=5.
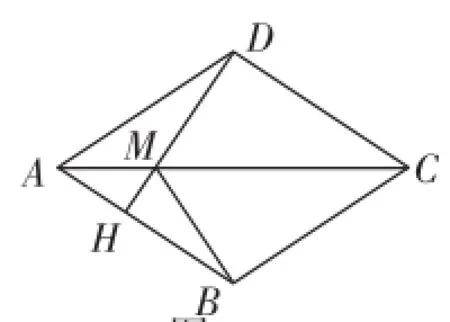
圖7
根據對稱性可得MD=MB.
總結:這是一道以菱形為背景的題,可以根據菱形的對角線互相垂直平分的性質,再利用面積相等法解之.
拓展4:如圖8,AD是△ABC的角平分線,以點C為圓心,CD為半徑作圓交BC的延長線于點E,交AD于點F,交AE于點M,且∠B=∠CAE,EF∶FD=4∶3,DE=10.求線段ME的長.
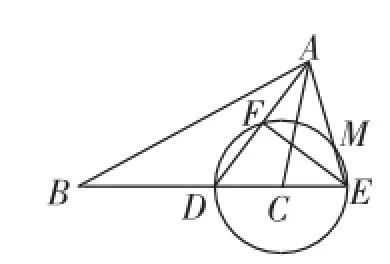
圖8
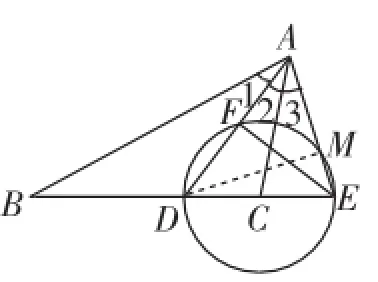
圖9
分析:如圖9,連接DM,則DM⊥AE.
由AD是△ABC的角平分線,得∠1=∠2.
又∠ADE=∠1+∠B,∠DAE=∠2+∠3,且∠B=∠3,則∠ADE=∠DAE,則ED=EA=10.
由ED為⊙O的直徑,得∠DFE=90°,則EF⊥AD,則點F是AD的中點,故FD=FA.
總結:這是一道有關圓的綜合題,利用直徑所對的圓周角是直角,這樣就得到了三角形的高,從而很自然地想到了運用面積法求之.
二、根據等高(底)的兩個三角形的面積之比等于對應底邊(對應高)的比的性質等進行解題
問題2:如圖10,在△ABC中,∠BAC=60°,AB=7,AC=6,過C作CE⊥CA,交AB的延長線于E,AD是∠BAC的平分線,過B作BP∥EC,交AD于P,連接CP,過B作BF∥PC,交AC的延長線于F,求線段CF的長.
分析:在Rt△ECA中,由∠BAC= 60°,得∠E=30°,所以AE=12,所以BE=5.
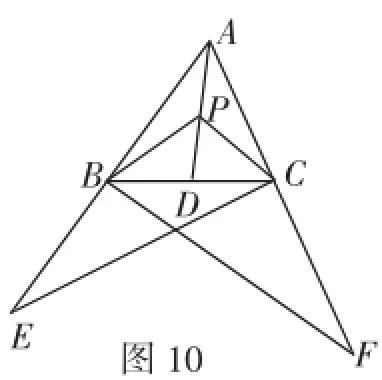
圖10
由于點P在∠BAC的平分線上,而BE、CF同時在這個角的兩邊上,所以P到BE、CF的距離相等,即△PBE與△PCF的兩條高相等.
由CE∥PB,可得S△PBE=S△PBC.
同理S△PCF=S△PBC.則S△PBE=S△PCF,進而可以求出CF=BE= 5.
總結:根據等高的兩個三角形的面積之比等于對應底邊的比的性質,可以通過證明等高的兩個三角形的面積相等,證得對應的底邊相等,從而求得有關線段的長.
變式:如圖11,在△ABC中,DE∥BC,交AB于D,交AC于E,AF∥EB交CB于F,AG∥DC交BC于G,如果BF= 5,求線段CG的長.
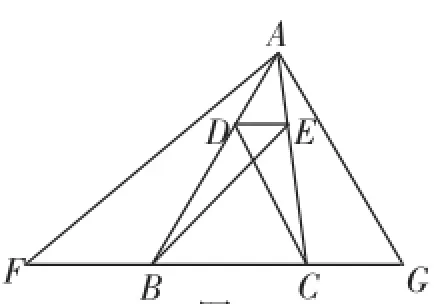
圖11
分析:通過觀察圖形,連接EF、DG.
由于△EBF和△DCG是等高的兩個三角形,要證BF= CG,只要證明S△EBF=S△DCG.
由AF∥EB,可得S△EBF=S△ABE同理,S△ADC=S△GCD.
由DE∥BC,得S△BDE=S△CDE.同加上S△ADE,可得S△ABE= S△ACD.
所以得到S△EBF=S△DCG,根據如果等高的兩個三角形的面積相等,那么它們對應的底邊相等,可得到線段CG=5.
總結:此題更一般化,根據平行線間的距離處處相等,先得出同底的兩個三角形的面積相等,再利用等高的兩個三角形的面積之比等于對應底邊的比的性質,通過證明等高的兩個三角形的面積相等,證得對應的底邊相等,從而求得有關線段的長.
總之,面積法是一種重要的解題方法,借助面積法可以把幾何問題中的線段關系或其他量與量的關系轉化為面積關系來解決,從而起到化繁為簡、化難為易的作用.
1.彭翕成,張景中.仁者無敵面積法[M].上海:上海教育出版社,2011.

