數控自動換刀機械手的運動分析

張繼紅（四川職業技術學院，四川　遂寧　629000）

數控自動換刀機械手的運動分析

張繼紅
（四川職業技術學院，四川遂寧629000）

數控機床的先進性不僅表現在其控制系統和機床主體的先進性上，而且其輔助功能，諸如自動換刀，自動裝夾等也體現了先進性.自動換刀系統首要解決的就是換刀時運動的準確要求，才能保證準確地從主軸上卸刀并放入刀庫中，才能保證準確地從刀庫里取出下一把刀并裝入主軸上.同時也希望自動換刀機械手具有靈活，通用的特性.文章對換刀機械手進行了正運動和逆運動分析，解決了機械手換刀的位置問題.

數控換刀；機械手；運動分析

古代人們就夢想著能制造出類似于人類自身的某種裝置，來代替人完成人們的日常作業工作，以便減輕或者代替人的某些勞動.據記載中國三國志中的諸葛亮曾經制造過“木牛流馬”幫助部隊運送糧草.大藝術家科學家達芬奇也曾設計和制造過很復雜的機械裝置，來取代人的某些功能.而機器人時代的到來則是現代科學技術的結晶，其歷史也不過幾十年.1961年世界上第一臺工業機器人問世，其名曰“Unimati”.隨后機器人技術及應用迅猛地發展起來了.機器人技術是高科技發展的重要方向之一，機器人學成為研究機器人及其相關技術的科學，是涉及到精密機械，電氣，微電子，計算機技術，控制技術，傳感技術和人工智能的綜合學科.

數控加工中心上的傳統換刀裝置只能算一種機構而已，起止位置固定，把不同工序使用的刀具從主軸卸下放入刀庫，把下一把刀具從刀庫取出裝入主軸.采用自動換刀機械手后換刀具有很好的柔性，如圖1.機械手換刀首先需要解決的就是手部起止位姿的求解，即機械手運動分析.

1　換刀機械手正運動分析

要實現對換刀機械手空間軌跡的控制，完成精確的換刀作業，就需要求解工業機械手在空間的位置和姿態.即對機器人進行運動學分析，包括正運動學和逆運動學分析.

機器人手部的位置就是從某基準坐標所描述的位置矢量（x,y,z）.而姿態表示抓取物體的方向（α，β，γ）.正運動學分析就是從關節角求出機械手末端的位姿，逆運動學分析則是由機械手末端位姿求出各關節角如圖1.

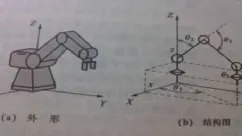
圖1　

1.1手部的位姿描述

手部的位姿可用坐標系來描述，如圖2.

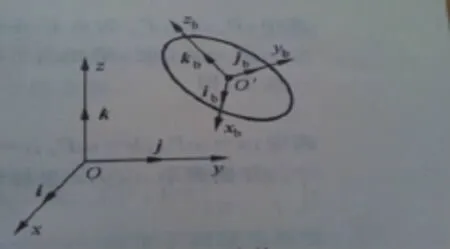
圖2　

設｛O：x,y,z｝為固定坐標系，｛Oˊ：xb,yb,zb｝為動坐標系，且動坐標系由固定坐標系經平移，旋轉而來.那么機械手部的空間位置可用動坐標系的原點Oˊ在固定坐標系中的位置表示：

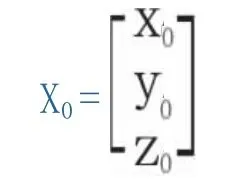
而手部的空間姿態則可以用動坐標系的三個單位向量ib，jb，kb的方向來表示，就是動坐標相對于固定坐標的方向余弦（i*ib，j*ib，k*ib）,（i*jb，j*jb，k*jb）,（i*kb，j*kb，k*kb），其中i，j，k是固定坐標系單位向量.即：

收稿日期：2015-05-04

作者簡介：張繼紅(1965-)，男，四川遂寧人，四川職業技術學院副教授.研究方向：機器人，先進制造技術.

［ibjbkb］=［i j k］*R

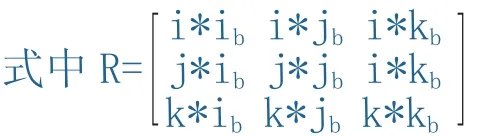
知道了機械手手部的空間位置和手抓的方向，那么其抓取物體就沒有問題了.

1.2手部的齊次坐標變換

要求解機械手手部的位姿和關節角需要進行齊次坐標變換，以建立手部和關節的位置關系，從而求解未知的參數.坐標的齊次變換就是將n維空間的點用n+1維坐標表示.在空間坐標系{O：x,y, z}中任一點的位置矢量P,則有：

P=［PXPYPZ1］T

單位矢量i，j，k齊次坐標描述為：

X=［1 0 0 0］T

Y=［0 1 0 0］T

Z=［0 0 1 0］T

假如有一簡單的一連接桿的機械手，在機器人坐標系中，相對于連接桿不動的設為固定坐標，例如基座；而手部關節隨連接桿有運動的設為動坐標.這一機器人手持加工刃具進行作業加工，若基座固定坐標系為｛O：x,y,z｝，手部動坐標系為｛Oˊ：xb,yb,zb｝.刃具中心P相對于固定坐標系其坐標是（x,y,z），相對于動坐標系坐標是（xb,yb,zb），手部中心Oˊ在固定坐標系的坐標是（x0,y0,z0），則三個矢量關系為：

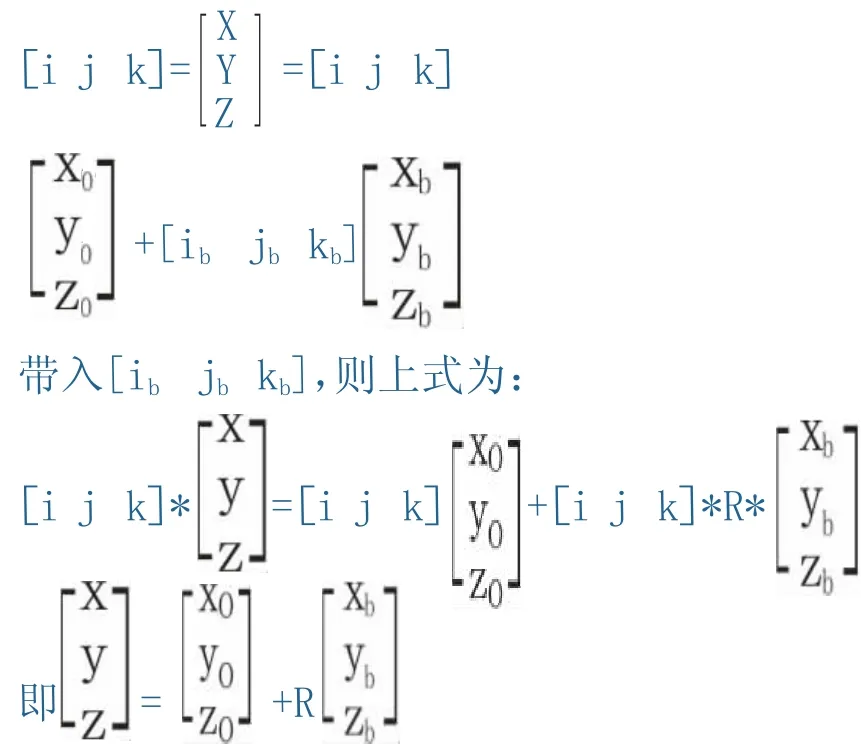
若令X=［x,y,z］T,Xb=［xb,yb,zb］T,X0=［xo,yo,zo］T,則得坐標變換方程：

X=X0+RXb

通常機械手都是多連桿，多關節，多自由度的，故從手部到基座可以通過一系列坐標變換求得，其合成的坐標變換矩陣描述為：

T=T1T2T3…Tn

2　換刀機械手逆運動分析

通過機械手的正運動分析，可以從機座開始經過一系列的已知連桿關節的運動求解手部的目標位置姿勢.而加工中心換刀機械手的設計則正好相反，往往是已知的某一把刀具在刀庫中的位置，機械手從已知位置取刀后要裝入已知位置的主軸上，需要求解各關節的位姿值，從而利用計算機控制關節微電機實現手部的位姿要求，順利完成換刀動作.這就需要機械手的逆運動分析.對于多關節機械手結構分析時先畫出其坐標系中的結構圖，用它來描述機械手各軸的關節角度（θ1，θ2，θ3，…θn），及手部的位置姿勢(x,y,z，α，β，γ).

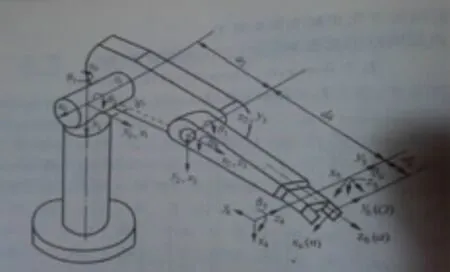
圖3

圖3所示機械手根據已知的末端條件，利用某一解法可以求出各關節變量的函數.通常運用變換矩陣的逆矩陣左乘找出右端為常數的元素，并令其與左端相等求出三角函數方程，重復上述求出其余未知數.這樣可依次求解關節變量θ1，θ2，θ3，…θ6.

3　結論

先進制造技術中最重要的設備就是加工中心.其自動換刀機械手要可靠，準確，靈活地完成主軸上前把刀具的卸下入庫和后一把刀具的取出并裝上，最基本的就是要先完成機械手的運動分析.由于機械手都是在特定的空間作業，故涉及的坐標系很多，分析的數學方法多樣.通常要尋找計算機能計算的方法為佳.文章應用固定坐標系與多重動坐標系的關系，利用矩陣方法進行變換，求解變換矩陣，進行機械手從機座到手部的正運動分析.再應用坐標變換矩陣的逆矩陣左乘進行逆運動分析，求解各關節的變量.以完成機械手的運動設計.參考文獻：

[1]韓建海.工業機器人[M].武漢:華中科技大學出版社,2012.

[2][日]三浦宏文.機電一體化[M].北京:科學出版社,2003.

[3]周宏甫.數控技術[M].廣州:華南理工大學出版社,2005.

[4]李宏勝.機床數控技術及應用[M].北京:高等教育出版社,2005.

[5]張迪妮.先進制造技術[M].北京:北京大學出版社,2006.

責任編輯：張隆輝

TG 596

A

1672-2094（2015）04-0156-03