三相并網逆變器靜止坐標系零穩態誤差電流控制分析及在線切換控制研究

郭小強 賈曉瑜 王懷寶 盧志剛 孫孝峰 張純江

（燕山大學電力電子節能與傳動控制河北省重點實驗室（燕山大學）秦皇島 066004）

1 引言

作為分布式發電系統與電網的接口裝置，三相并網逆變器得到了廣泛的關注和應用[1,2]。為了實現三相逆變器高效穩定并網運行，需要解決一系列的技術挑戰。其中，電流控制技術是三相逆變器并網運行最基本的技術要求之一[3]。眾所周知，分布式發電系統并網運行的基本目標是向電網發送有功或無功功率，而功率與電網電壓和并網電流有關。由于電網電壓很難調節，此時必須對并網電流進行調節來達到控制功率的目的[4]，因此，電流控制技術是逆變器并網運行的關鍵問題。

實際應用中，快速性和精確性是評價三相并網逆變器電流控制的兩大指標。例如，分布式發電系統低電壓穿越時，要求系統動態響應時間小于一個工頻周期（20ms）[5]，這無疑需要高性能的電流控制策略。另一方面，為了保證精確的電流控制，要求控制器具有零穩態無差控制特性。旋轉坐標系PI控制是目前廣泛采用的并網電流控制方法，可以實現并網電流的零穩態無差控制[6]，但該方法需要旋轉坐標變換，計算量較大，增加了系統實現復雜度。為了解決此問題，文獻[7]探討了一種靜止坐標系比例諧振 PR控制方法，該方法無需旋轉坐標變換，計算量小，同時可以實現零穩態誤差控制，因此引起國內外學者的高度關注，在并網電流控制中得到廣泛應用[8]。雖然諸多文獻對PR控制的性能和特點進行研究和探討，但有些問題仍值得商榷。如大部分文獻認為靜止坐標系PR控制和旋轉坐標系PI控制兩者等效，然而這一觀點并不完全正確。文獻[7]指出靜止坐標系PR控制比旋轉坐標系PI控制動態響應慢的問題，說明兩者之間具有一定的差異，并非完全等效。此外靜止坐標系 PR控制動態響應慢的現象文獻[7]并未給出合理的解釋。另一方面，文獻[9]提出一種比例復數積分PCI控制，該控制無需旋轉坐標變換，同樣可以實現并網電流的零穩態誤差控制，還具有和PR控制相似的數學表達式。讀者不禁會產生這樣的疑問：兩種控制之間是否有內在的聯系？實際應用如何在兩種控制方案之間做出選擇？哪種控制方案更優？本文將針對上述問題開展有意義的研究和探索。

本文主要工作如下：①通過理論分析證明靜止坐標系 PR控制和旋轉坐標系 PI控制兩者并不等效，這也是靜止坐標系PR控制比旋轉坐標系PI控制動態響應慢的重要原因之一。②深入分析了靜止坐標系PR控制和PCI控制在動態性能和穩態性能方面的特點，提出在線平滑切換方案有效利用兩者的優勢，最后在不同電網工況下對兩種控制方案及其在線切換方案進行實驗驗證。

2 三種控制內在聯系

本節首先從旋轉坐標系PI控制入手，通過理論分析研究旋轉坐標系PI控制、靜止坐標系PR控制和靜止坐標系PCI控制三者之間的聯系和區別。圖1為旋轉坐標系PI控制的結構框圖。

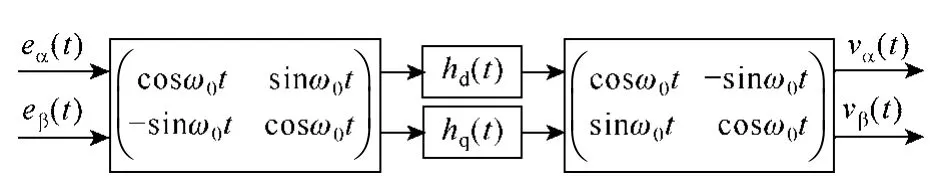
圖1 旋轉坐標系PI控制Fig.1 Synchronous rotating frame PI control

如圖1所示，首先，靜止坐標系誤差信號eα(t)和eβ(t)通過旋轉坐標變換得到 dq軸誤差信號，然后經過PI調節器，再通過反旋轉坐標變換得到靜止坐標系輸出信號vα(t)和vβ(t)。

根據圖2可得

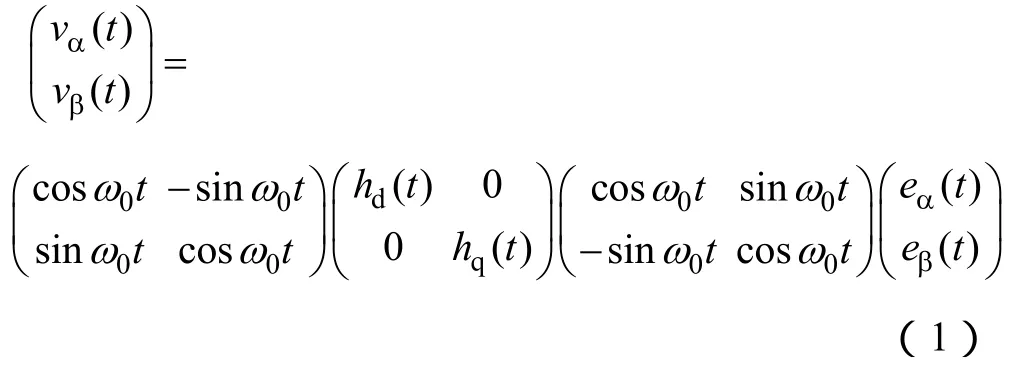
式中，hd(t)=hq(t)=KP+KI/s。

將式（1）進行Laplace變換并化簡可得

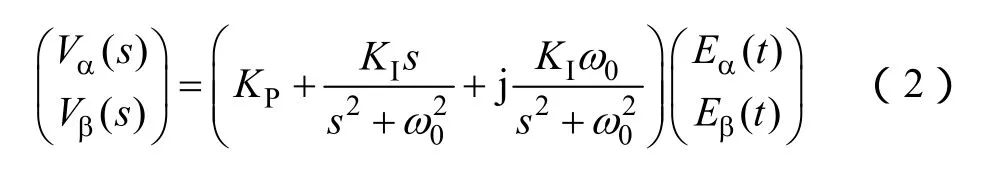
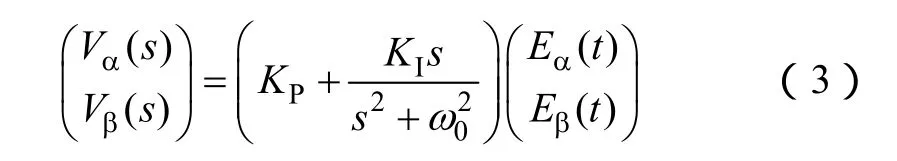
根據上述分析可知，由于忽略了復數項，旋轉坐標系PI控制和靜止坐標系比例諧振PR控制兩者并不等效。

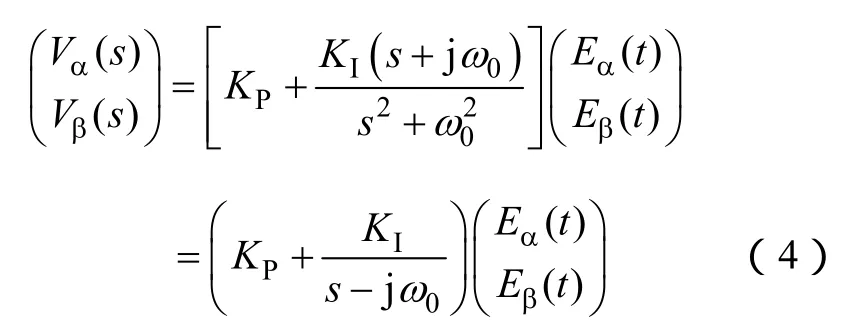
根據上述分析可知，由于考慮了復數項，旋轉坐標系PI控制和靜止坐標系比例復數積分PCI控制兩者完全等效。

綜上，靜止坐標系PR控制和PCI控制存在密切的聯系，兩者均可以從旋轉坐標系PI控制推演得到，唯一不同的是，PR控制未考慮復數項，因此旋轉坐標系PI控制和靜止坐標系比例諧振PR控制兩者并不等效。而PCI控制充分考慮了復數項，因此旋轉坐標系PI控制和靜止坐標系比例復數積分PCI控制兩者完全等效。這唯一的區別導致兩種控制策略性能出現較大差異。下節將從穩態和動態響應對兩種控制策略進行性能評估。

3 PR和PCI控制性能評估

下面以三相并網逆變器電流控制為例對靜止坐標系PR和PCI控制策略進行性能評估，原理圖如圖2所示。

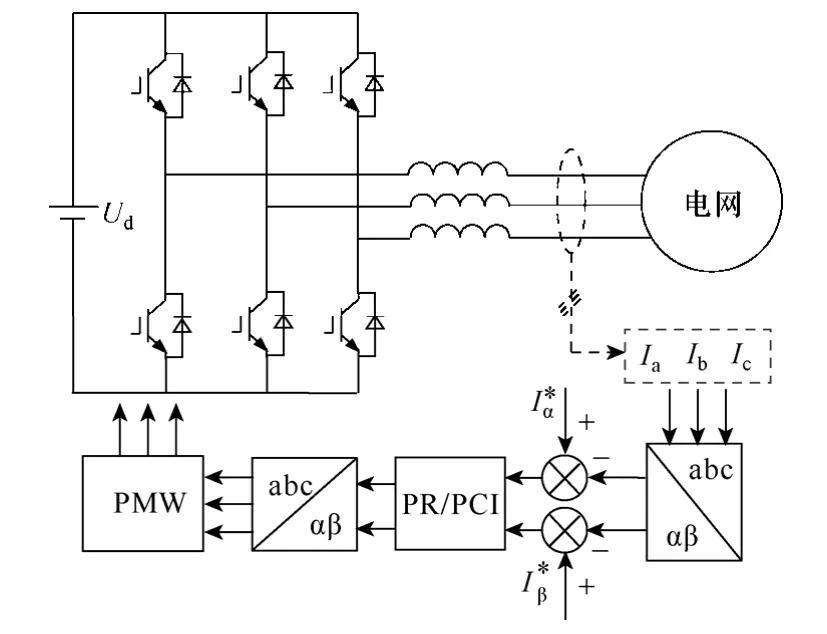
圖2 三相并網逆變器控制原理圖Fig.2 Control diagram of three-phase grid-connected inverter

圖 2中，三相并網電流Ia、Ib、Ic經過 Clarke變換得到αβ坐標系電流信號，與并網電流參考指令和相減得到誤差信號，然后經過PR或PCI控制器，再經過反Clarke變換得到abc坐標系輸出信號，將該信號作為調制波送至 PWM發生器，產生驅動開關的六路邏輯信號，逆變器通過閉環控制輸出三相正弦并網電流。為了評估兩種控制策略的性能，首先建立系統閉環控制模型，如圖3所示，其中，C(s)為電流控制器，R為電感L的等效串聯電阻，K為PWM等效增益，Io(s)和(s)為并網電流及其參考指令。Ug(s)為電網電壓。

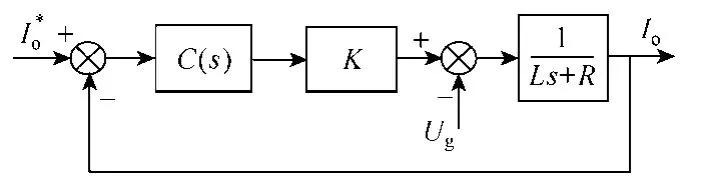
圖3 系統閉環控制模型Fig.3 System closed-loop control model

根據圖3可得并網電流為

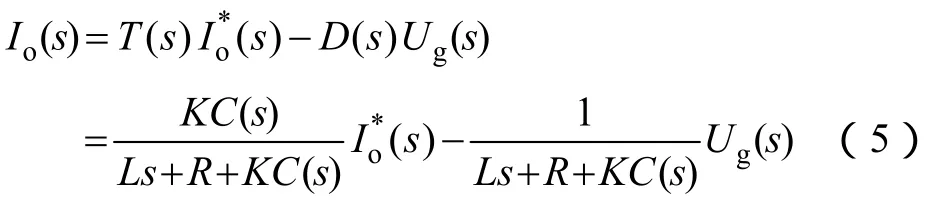
式中，T(s)和D(s)分別為并網電流參考跟隨特性和抗擾特性的傳遞函數。根據式（5）可知，并網電流不僅和參考指令(s)和電網電壓Ug(s)有關，還和控制器C(s)關系密切。一般而言，采用適當的并網同步方案可以保證參考指令(s)為三相平衡正弦電流。但對于電網電壓，實際應用中可能出現三相電壓不平衡，此時必須選擇合適的控制器C(s)，保證并網電流不受影響。

3.1 穩態性能評估

下面根據疊加定理分別對并網電流參考跟隨特性T(s)=Io(s)/(s)和抗擾特性D(s)=Io(s)/Ug(s)進行分析。將式（5）中 PR控制和式（6）中 PCI控制傳遞函數表達式代入式（5）可得

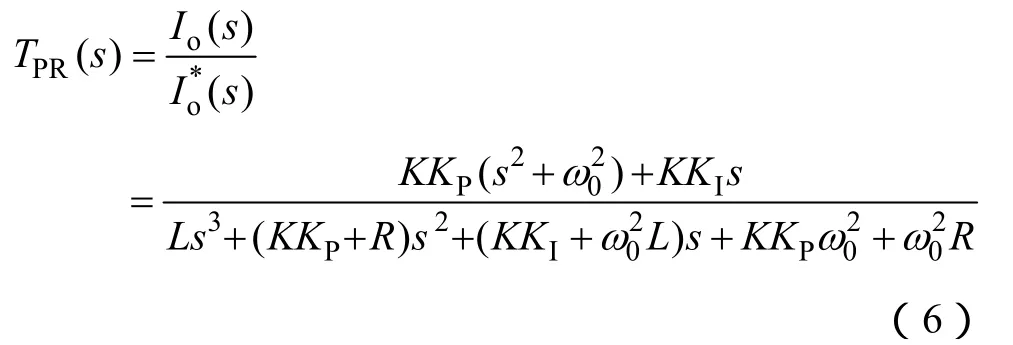
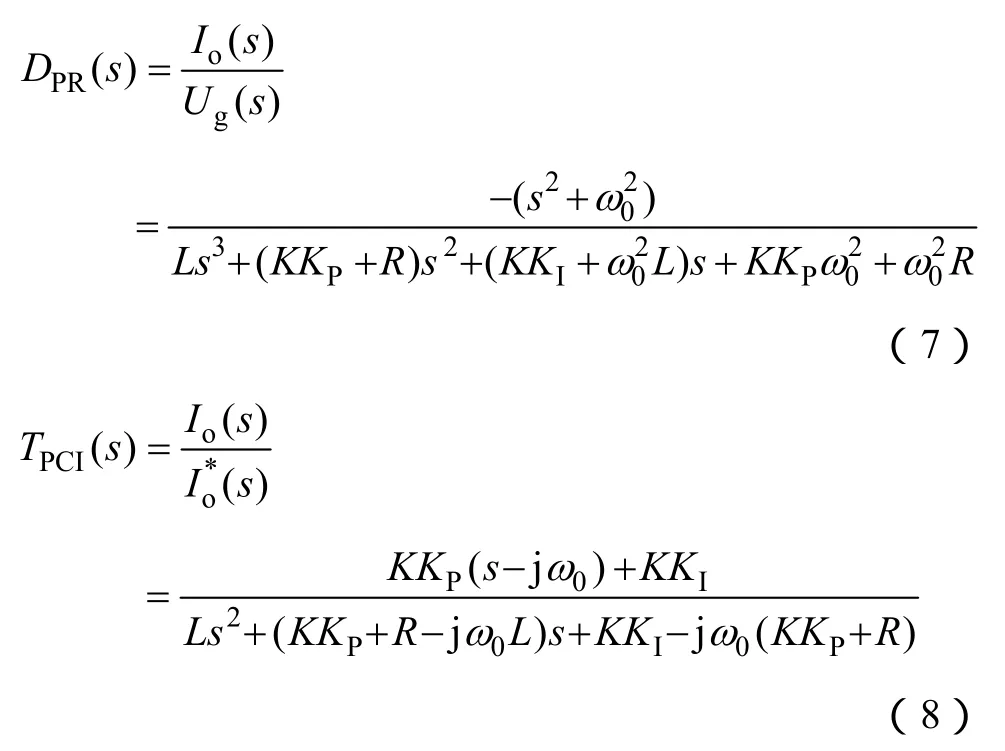
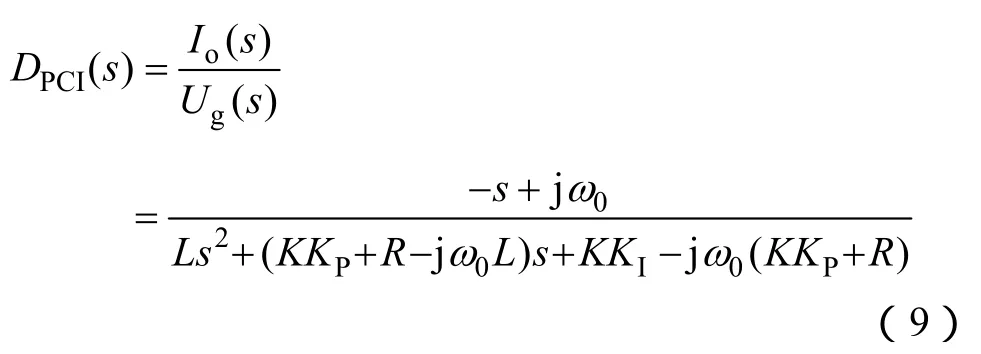
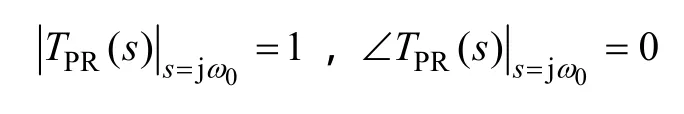
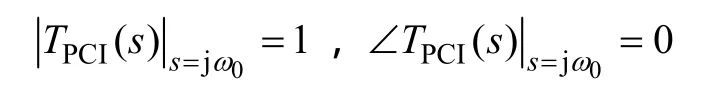
然后考慮兩種控制策略的抗擾特性。當電網電壓出現不平衡時，Ug(s)中不僅包含基波正序分量，還包含基波負序分量。若要實現并網電流不受電網電壓影響，需滿足D(s)在基波正序分量頻率ω0和負序分量頻率-ω0處幅頻特性均為 0。很明顯，PR具備上述特性，PCI在正序頻率ω0具備上述特性，但在負序頻率-ω0處不具備上述特性，即

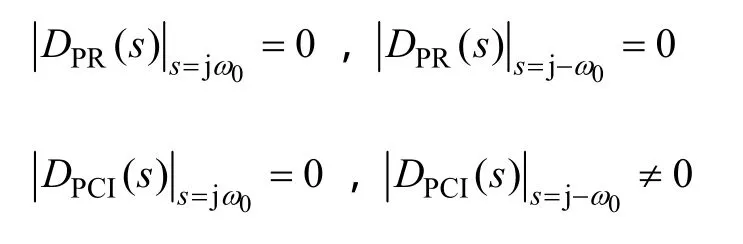
因此，當電網電壓平衡時，PR和PCI均可以實現并網電流的精確控制。另一方面，當電網電壓不平衡時，PR可以實現并網電流的精確控制，而PCI由于在電網電壓負序頻率處抗擾特性不為 0，導致并網電流無法精確控制。

3.2 動態性能評估

下面對PR和PCI控制策略動態性能進行分析。閉環極點是系統動態性能常用的方法之一。一般而言，閉環極點具有負實部，說明系統穩定；閉環極點具有虛部，說明系統暫態過程會出現振蕩，振蕩頻率由虛部數值大小決定；閉環主導極點距離虛軸越遠，說明系統穩定裕度越大、動態響應越快。閉環極點由系統特征方程決定，根據式（6）可知PR控制系統特征方程為

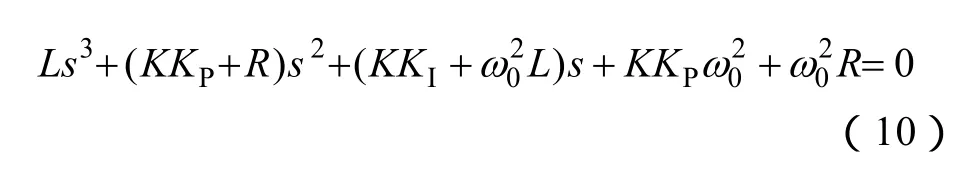
根據式（8）可知PCI控制系統特征方程為

下表給出不同控制參數（主電路參數見第5節）情況下系統閉環極點分布。如上文所述，PR控制和PCI控制極其相似，均在不同程度上與同步旋轉坐標系PI控制等效，唯一的區別是PCI考慮復數項，而 PR未考慮復數項，這唯一的區別導致兩種控制策略性能出現較大差異。見表中所示，相同控制參數情況下，PR控制系統閉環主導極點離虛軸相對較近，而PCI控制系統閉環主導極點離虛軸相對較遠，因此，與PR控制相比，PCI控制穩定裕度相對較大、動態響應相對較快，上述結論將通過仿真和實驗驗證。

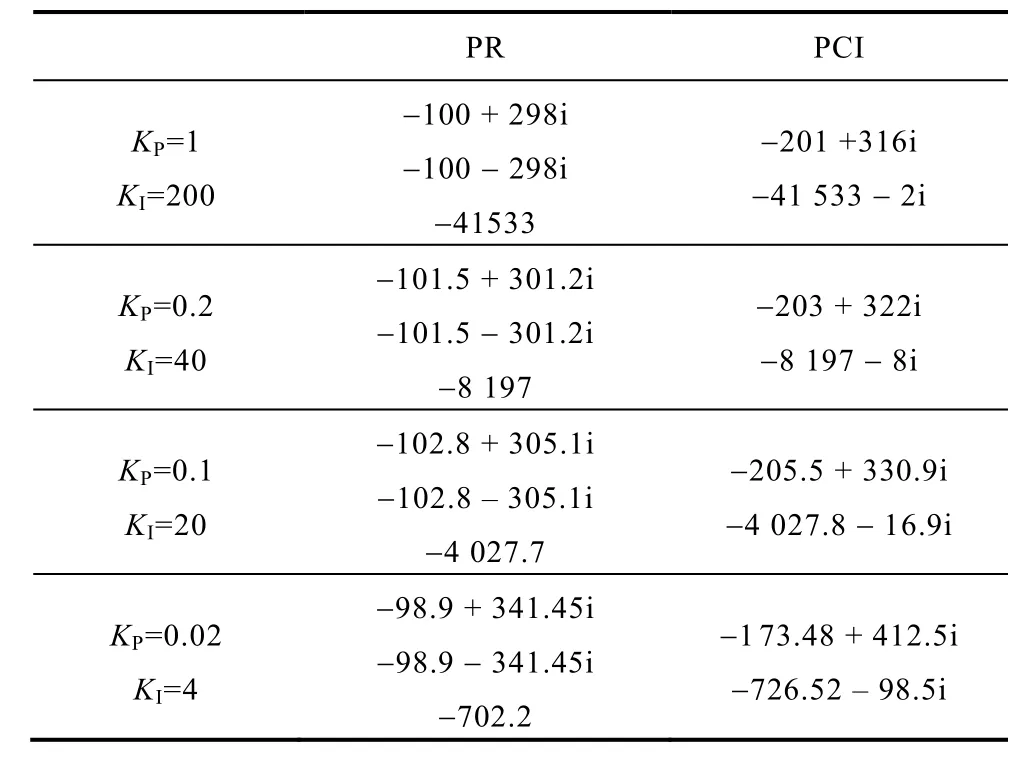
表 系統閉環極點Tab. System closed-loop poles

3.3 物理結構評估

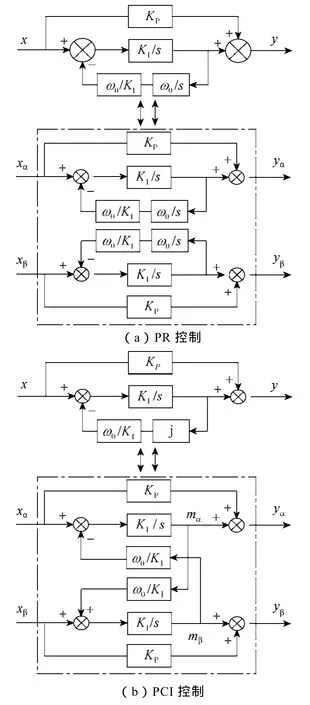
圖4 PR和PCI控制物理實現Fig.4 Physical implementation of PR and PCI controls

下面對PR和PCI控制物理結構進行評估。圖4為兩種控制方案的原理圖，可以看出，兩者結構極其相似，唯一的區別是 PR控制積分回路反饋時采用ω0/s，而PCI控制采用的是j。

值得注意的是，圖4a中兩個ω0/s實現時需要積分（1/s）和乘法（乘ω0），而圖4b中j無需積分和乘法，只需將反饋量實時交叉即可。因此，與 PR控制相比，PCI控制結構更簡單、實現更簡便。此外，和文獻[9]結論一致，當ω0=0時，圖4a和圖4b均轉化為PI控制的原理圖。

4 PR和PCI控制在線切換

實際應用中，正常情況下電網電壓不平衡度小于2%，短時不平衡度小于4%。根據上文分析可知，從系統穩態控制精度和動態響應速度考慮，推薦采用PCI控制。另一方面，當電網出現不平衡故障（如低電壓穿越）時，推薦使用 PR控制。值得注意的是，電網不對稱故障（如低電壓穿越）一般時間較短[5]，三相并網逆變器大部分時間處于電網非故障狀態運行，對于動態性能要求較高的場合，此時可采用PCI控制保證大部分時間內并網電流的零穩態誤差控制和快速動態響應；當檢測到電網不對稱故障時可切換至 PR控制，實現并網電流的精確控制。

為了實現上述目標，需要解決兩個關鍵問題：一是控制切換準則；二是如何確保兩種控制快速平滑切換。如上文所述，切換準則主要根據電網電壓不平衡度確定，其中不平衡度定義為負序分量和正序分量之比。因此只要計算出正序分量和負序分量就可以很容易確定電網電壓的不平衡度。現有相關方案很多，如雙旋轉坐標系鎖相環[10]或自適應陷波器[11]等，均可以快速準確計算出正序分量和負序分量，進而確定不平衡度。當電網電壓不平衡度高于4%時，說明電網處于非正常情況，此時可由 PCI控制切換至 PR控制，實現并網電流的精確控制；當電網電壓不平衡度低于 4%時，說明電網處于正常情況，此時可由PR控制切換至PCI控制。

圖 5a為控制切換的基本方式（方案 1），當開關置于上方時為PR控制，開關置于下方為PCI控制。此種切換方式較為直觀，但兩者切換時控制結構變動較大，容易引發較長時間的暫態響應。為了解決此問題，本文提出一種新型切換方式，如圖5b所示?？紤]到PCI和PR控制結構的相似之處（見圖4），方案2只對控制支路進行切換，不改變控制主體結構，即控制主回路為PI控制不變，只切換反饋支路，從而解決切換時控制結構變動較大的問題，有助于PCI和PR控制在線平滑切換。

圖5 PR和PCI控制在線切換方案Fig.5 Online transfer of PR and PCI controls

5 實驗結果

為了驗證本文理論分析的正確性，搭建了基于32位定點TMS320F2812 DSP的數字控制實驗平臺，DSP工作頻率150 MHz。直流側電壓250 V由直流穩壓電源提供，系統主電路拓撲如圖2所示，其中系統開關頻率10kHz，濾波電感3mH，交流側通過3kV·A三相變壓器和3kV·A單相調壓器接至三相電網，用于模擬三相電網電壓平衡狀態和不平衡狀態，控制器參數KP=0.1，KI=20，實驗結果如下。

5.1 三相電網電壓平衡

圖6a為三相電網電壓平衡情況下PR控制的實驗結果。和上文理論分析一致，PR控制可以消除并網電流的穩態誤差，并網電流暫態響應時間約為一個工頻周期。圖 6b為三相電網電壓平衡情況下PCI控制的實驗結果。可以看出，PCI控制可以消除并網電流的穩態誤差。和上文理論分析基本一致。對比圖6a和圖6b可知，與PR控制相比，PCI控制動態響應相對較快，驗證 3.2節理論分析的正確性。

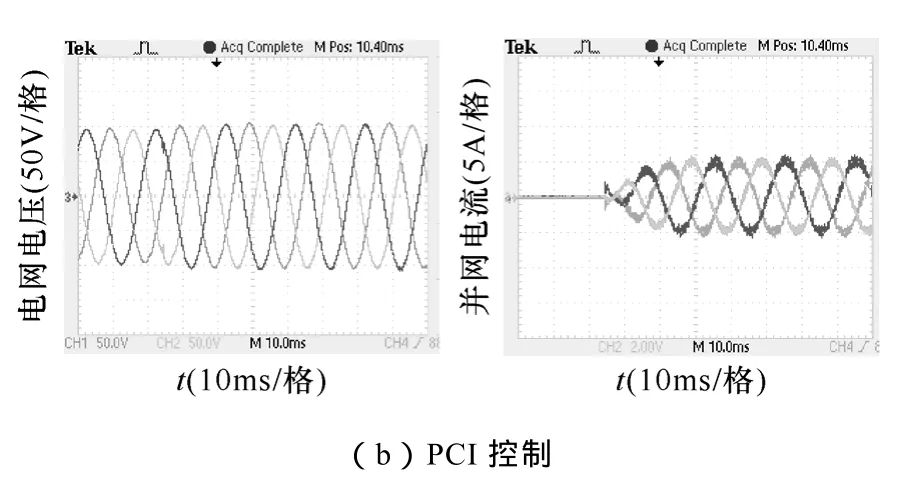
圖6 電網電壓平衡情況下實驗結果Fig.6 Experimental results under balanced grid voltage

5.2 三相電網電壓不平衡

圖7a為三相電網電壓不平衡情況下PR控制的實驗結果。和上文理論分析一致，由于 PR控制抗擾特性D(s)在基波正序分量頻率ω0和負序分量頻率-ω0處幅頻特性均為 0，因此可以有效抑制不平衡電網電壓對并網電流的影響，實現三相并網電流平衡正弦化。圖7b為三相電網電壓不平衡情況下PCI控制的實驗結果。和上文理論分析一致，由于PCI控制抗擾特性D(s)在基波負序分量頻率-ω0處幅頻特性不為 0，導致并網電流受電網電壓負序分量影響而無法精確控制，三相并網電流出現不平衡。

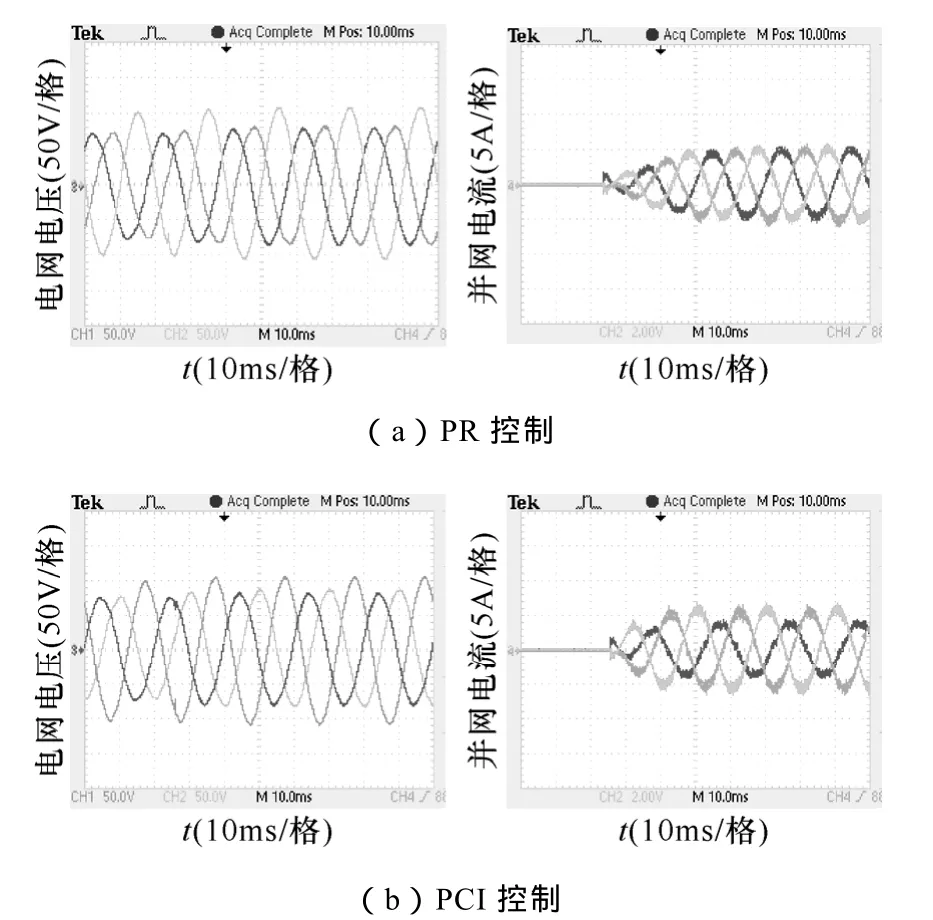
圖7 電網電壓不平衡情況下實驗結果Fig.7 Experimental results under unbalanced grid voltage

為了驗證本文提出的在線切換控制的有效性，下面對圖5切換方案進行實驗研究，實驗中通過觸發方式確定切換時刻，圖8為三相電網電壓不平衡情況下PR和PCI控制切換的實驗結果，和上文理論分析一致，采用方案1時，由于兩者切換時控制結構變動較大，導致切換過程暫態響應時間較長，如圖8a和圖8b所示。另一方面，采用本文提出的方案后，由于兩者切換時控制結構變動較小，切換過程暫態響應時間較短，如圖8b和圖8d所示，從而實現并網電流無沖擊在線平滑切換。

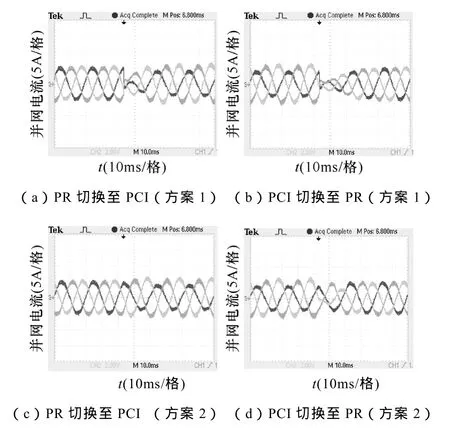
圖8 PR和PCI控制在線切換實驗結果Fig.8 Results of online transfer of PR and PCI controls

6 結論

本文深入分析了三相并網逆變器旋轉坐標系PI控制、靜止坐標系PR控制和靜止坐標系PCI控制三者之間的聯系和區別，證明了靜止坐標系 PR控制和旋轉坐標系PI控制兩者并不等效。通過對比分析靜止坐標系PR控制和PCI控制發現，兩者在動態性能和穩態性能方面各有特色，而本文提出的在線平滑切換方案可以有效利用兩者的優勢，具有良好的應用前景。

[1] 吳理博,趙爭鳴,劉建政,等. 具有無功補償功能的單極式三相光伏并網系統[J]. 電工技術學報,2006,21(1): 28-32.

Wu Libo,Zhao Zhengming,Liu Jianzheng,et al.Implementation of a single-stage three-phase grid connected PV system with reactive power compensation[J]. Transactions of China Electrotechnical Society,2006,21(1): 28-32.

[2] 蔣冀,段善旭,陳仲偉. 三相并網_獨立雙模式逆變器控制策略研究[J]. 電工技術學報,2012,27(2):52-58.

Jiang Ji,Duan Shanxu,Chen Zhongwei. Research on control strategy for three-phase double mode inverter[J]. Transactions of China Electrotechnical Society,2012,27(2): 52-58.

[3] Blaabjerg F,Teodorescu R,Liserre M,et al. Overview of control and grid synchronization for distributed power generation systems[J]. IEEE Transactions on Industrial Electronics,2006,53(5): 1398-1409.

[4] Sung K,Lee S,Dehbonei H,et al. Application of voltage- and current-controlled voltage source inverters for distributed generation systems[J]. IEEE Transactions on Energy Conversion,2006,21(3): 782-792.

[5] Tsili M,Papathanassiou S. A review of grid code technical requirements for wind farms[J]. IET Renewable Power Generation,2009,3(3): 308-332.

[6] Navid R,Goos J. Performance investigation of a current-controlled voltage-regulated PWM rectifier in rotating and stationary frames[J]. IEEE Transactions on Industrial Electronics,1995,42(4): 396-401.

[7] Zmood D N,Holmes D G. Stationary frame current regulation of PWM inverters with zero steady-state error[J]. IEEE Transactions on Power Electronics,2003,18(3): 814-822.

[8] 馬琳,金新民,唐芬,等. 三相并網逆變器比例諧振控制及其網壓前饋問題分析[J]. 電工技術學報,2012,27(8): 56-63.

Ma Lin,Jin Xinmin,Tang Fen,et al. Analysis of threephase grid-connected inverter proportional resonant control and grid voltage feed-forward[J]. Transactions of China Electrotechnical Society,2012,27(8): 56-63.

[9] 郭小強,鄔偉揚,趙清林,等. 三相并網逆變器比例復數積分電流控制技術[J]. 中國電機工程學報,2009,29(15): 8-14.

Guo Xiaoqiang,Wu Weiyang,Zhao Qinglin,et al.Current regulation for three-phase grid-connected inverters based on proportional complex integral control[J]. Proceedings of the CSEE,2009,29(15): 8-14.

[10] Rodriguez P,Pou J,Bergas J,et al. Decoupled double synchronous reference frame PLL for power converters control[J]. IEEE Transactions on Power Electronics,2007,22(2): 584-592.

[11] Yazdani D,Mojiri M,Bakhshai A. A fast and accurate synchronization technique for extraction of symmetrical components[J]. IEEE Transactions on Power Electronics,2009,24(3): 674-684.