基于混雜系統DC-DC變換器的永磁風電并網系統直流母線電壓穩定控制

張明銳 李元浩 歐陽麗 孫 華

（1. 同濟大學電子與信息工程學院 上海 201804 2. 上海電氣集團股份有限公司中央研究院 上海 200070）

1 引言

在風力發電系統中，當風速變化較為強烈時，將造成直流側電壓較為劇烈的波動，進而影響并網電壓的穩定[1,2]。此外，電網電壓的跌落將引起風電系統直流側電壓波動，甚至引起發電機側變流器功率失衡，風電機組脫網，對電網的穩定性和電能質量構成威脅，造成巨大損失[3-6]。

從以上兩個問題可以看出，為了保證聯網的穩定性和電能質量，抑制風電系統直流側電壓的波動是關鍵。因此本文在低壓直流側并聯超級電容器，在風力發電系統中通過雙向 DC-DC變換器對超級電容器快速充放電來恢復并維持直流母線電壓[7-9]。而 DC-DC變換器的拓撲結構及其控制方法對減少變換器工作狀態轉換過程中的超調，抑制直流母線電壓波動具有重要的意義。DC-DC變換器常用狀態空間平均[10,11]或電路平均[12]的小信號法作為主要建模與分析的方法。此方法便于系統穩定性分析以及控制器的設計，但由于小信號模型是通過忽略模型中高次項近似得到，因此當系統面對大信號擾動時（如電網電壓跌落），此方法具有局限性[13]。近年來，由于運用混雜系統理論建模精度高，無需近似處理，混雜系統被越來越多地應用于 DC-DC變換器的建模和控制。文獻[14]建立了DC-DC變換器在連續工作模式下混雜系統模型，提出一種基于李雅普諾夫的穩定條件的新型類滑模控制策略；文獻[15]使用包括滑模控制與邊界開關控制在內的幾何控制方法，得出混雜系統定義下二維變量 DC-DC變換器的deadbeat的控制策略。

考慮到 DC-DC變換器電路中既有連續變量又有離散變量，是一類典型的混雜動態系統，因此本文對 DC-DC變換器建立混雜系統模型，運用李雅普諾夫直接法分析系統穩定性，結合雙閉環控制方法，采用一種新型的類滑模控制策略[14]，實現對直流母線電壓的穩定控制。搭建永磁同步風力發電機并網系統模型，對電網電壓跌落及風機轉速變化兩種工況下直流側電壓穩定情況進行了仿真驗證。

2 新型風電并網系統結構

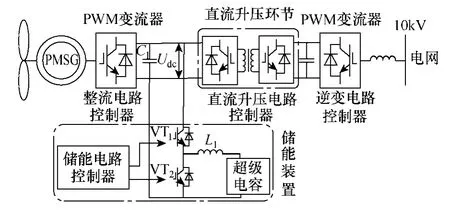
圖1 基于固態變壓器的永磁同步風力發電并網系統Fig.1 Permanent magnet synchronous wind-power generation grid-connection system based on solid state transformer

基于固態變壓器的新型永磁風電并網系統[16]如圖1所示，風機直接耦合永磁同步發電機的轉子，定子側輸出的交流電經整流器轉換為低壓直流，通過單相全橋逆變器調制成高頻方波，高頻變壓器將電壓升高后經單相全橋整流器轉換為直流，最后通過高壓側逆變器并網。該系統的特點是，在常規的風電系統變流器結構中加入高頻變壓器，通過固態變壓器實現常規風電系統的連接可使并網電壓提升至10kV，有利于實現系統擴容，并大幅減小并網電流，減小風電的間歇性對電網的頻繁沖擊，從而抑制并網電壓波動。

3 超級電容器

3.1 超級電容器模型

在新型風電并網系統的低壓直流側并聯超級電容器儲能裝置，有利于抑制功率波動并可提高風電機組自身的低電壓穿越特性。

超級電容器具有復雜的物理特性，可以用分布式參數來描述其數學模型，圖2為超級電容器經典電路模型[17]。

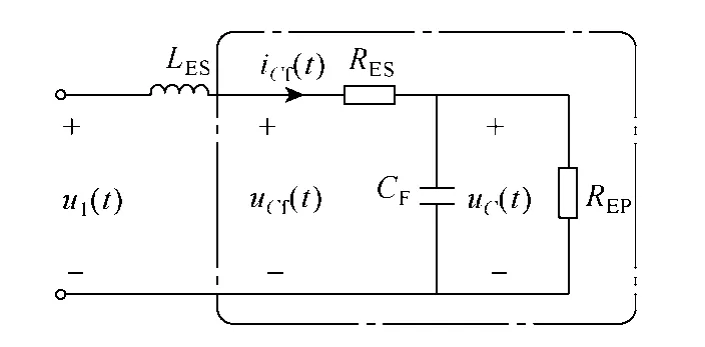
圖2 超級電容器的經典電路模型Fig.2 Classic circuit of double-layer super capacitor

3.2 超級電容容量計算

根據2009年12月22日頒布的國家電網公司企業標準 Q-GDW392-2009《風電場接入電網技術規定》第8章規定，風電場低電壓穿越要求如圖3所示，由圖可以計算出在電壓跌落期間直流母線兩側產生的能量差值，按三相短路情況計算。

式中，ΔP為電壓跌落時并網功率與其額定值的差值，積分上限為電網電壓跌落時間2s。

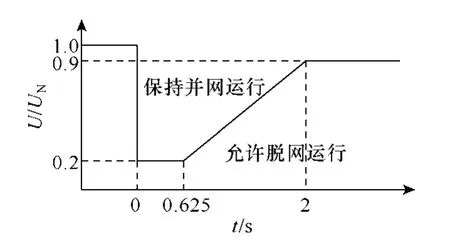
圖3 風電場的低電壓穿越要求Fig.3 Low voltage ride through requirement of wind farm

通過對圖3中電壓跌落部分積分可以計算出，由于并網功率減小而導致在直流母線兩側產生的不平衡能量總和約為1.2MJ[18]。

根據風電系統的配置參數，本文儲能電路中的超級電容選擇：電容容量50F，額定電壓540V，實際電路由 200個 10 000F，2.7V的單體串聯而成。

3.3 超級電容初始電壓

當風力機不能提供足夠電能，需要超級電容器釋放電能維持直流側電壓的穩定。超級電容充電到預先設定初始電壓uCf_ref，其計算公式為[19]

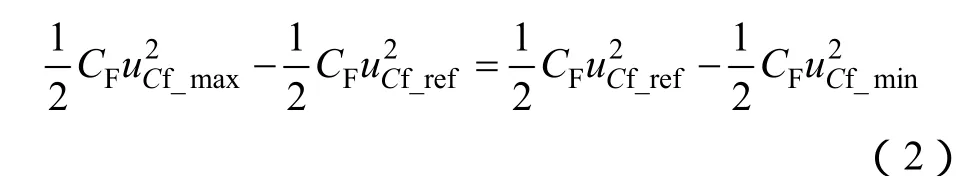
式中，CF是超級電容的電容量；uCf_max和uCf_min分別為超級電容的最高充電電壓和最低放電電壓。

3.4 電感值的計算

當電感電流臨界連續時，等效串聯電感LES的計算公式為[20]

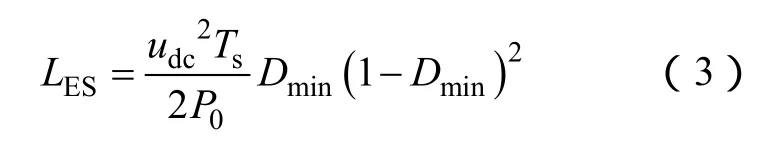
式中，udc為并網變流器的直流母線電壓；Ts為開關周期；P0為并網變流器向電網輸送的最大有功功率；Dmin為DC-DC變流器開關管VT2的最小占空比。

4 雙向DC-DC變換器混雜系統建模與穩定性分析

為了充分發揮超級電容器充放電特性，將超級電容器通過雙向 DC-DC變換器接到風力發電系統的直流母線上。當直流母線電壓升高時，超級電容器通過雙向 DC-DC變換器充電，吸收電能；當直流母線電壓下降時，超級電容器通過雙向 DC-DC變換器釋放電能到直流母線。因此，高效準確地控制 DC-DC變換器，是維持直流母線電壓穩定的關鍵技術。

由于DC-DC變換器中存在IGBT電力電子開關器件，從而使系統模型不連續。在風力發電系統中，隨著直流側母線電壓的波動和超級電容器工況（如某一開關時刻的到達，電流或電壓超過一定閾值）的變化，開關器件在不同的Buck-Boost電路間發生切換，體現出離散事件動態系統的特征。而每一個電路拓撲中的狀態變量（如電流、電壓等）隨著時間連續動態地發生變化，體現出連續時間動態系統的特征。離散事件和連續時間動態特性相互作用，使 DC-DC變換器呈現混雜系統的動態特征。

4.1 DC-DC變換器系統模型

若將能量耗散的概念引入到端口受控哈密頓系統框架中，則根據耗散的端口受控哈密頓系統，連續工作模式下的基本DC-DC電路可以表示為[21]

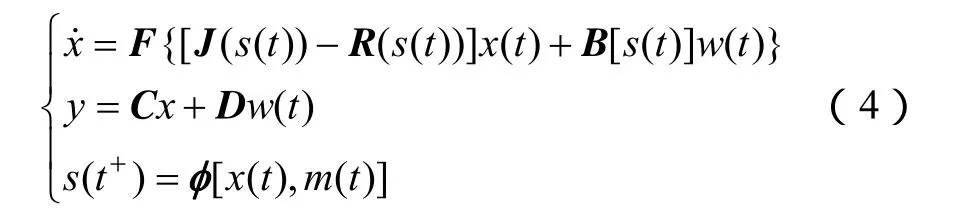
式中，系統連續時間狀態量x(t)是電感電流和電容電壓；F、J和R均為n×n陣，其中F為可逆陣，取值與主電路參數相關，每個元素大于零，J為斜對稱陣，R為與負載電阻相關的非負矩陣；B∈Rnr×為輸入矩陣；w(t)為連續輸入量；C∈Rmn×為輸出矩陣；D∈Rmr×為直接轉移矩陣；m(t)表示系統當前模態的離散事件的輸入，φ(·,·)是以系統狀態x(t)和離散事件m(t)為變量的不連續函數，即系統的控制策略不但取決于狀態變量，也由m(t)決定，而這也是混雜系統與一般切換系統的不同之處；s(t)∈{0,1}為布爾量，體現了整個系統的控制結果。

4.2 基于Boost電路建模

基于 Boost電路建立混雜系統模型，在 Boost電路中含有一個可控開關（即開關管V）和一個不可控開關（即功率二極管VD），為了討論方便，本文用理想開關s表示可控開關器件，并假設各開關導通時值為1，截止時為0。如圖4所示，基于基爾霍夫電壓定律和電流定律的狀態方程表示為

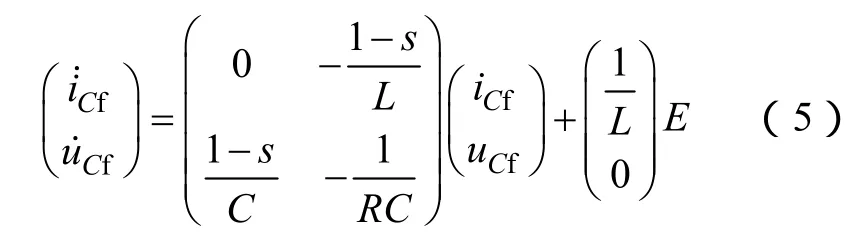
圖4 簡化后的Boost電路拓撲圖Fig.4 The schematic of a simplified Boost converter

按照混雜系統式（4）確定各系數矩陣取值

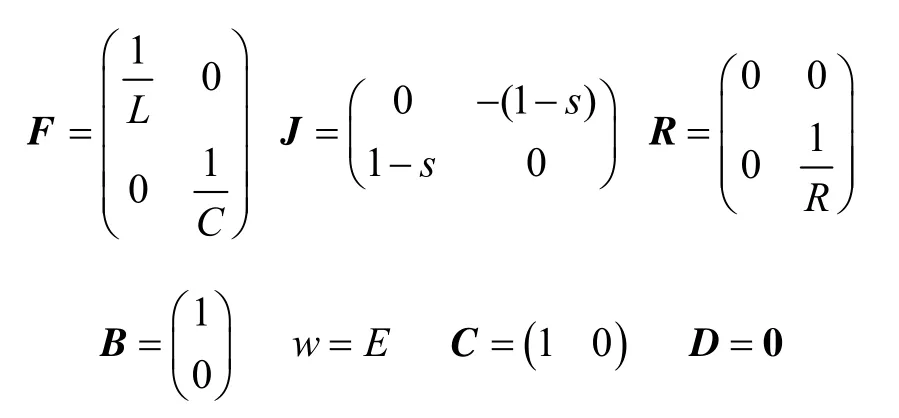
當s=1時，開關s導通，關斷；反之當s=0時，開關s關斷，導通。因此 Boost電路模型既有離散事件又體現了連續時間動態特性，二者相互作用，呈現出典型的混雜系統的動態特征。

4.3 系統平衡點與李雅普諾夫漸近穩定條件

在討論系統穩定點時，把開關量s看作為一個連續量s(t)，然后先選擇系統狀態穩定點x(t)=xref，當存在s(t)=seq，且0≤seq≤l，滿足

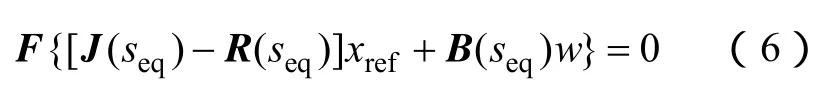
由式（6）計算出在Boost電路中電壓和電流的平衡點uref和iref分別為

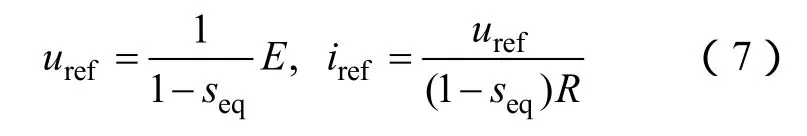
其中

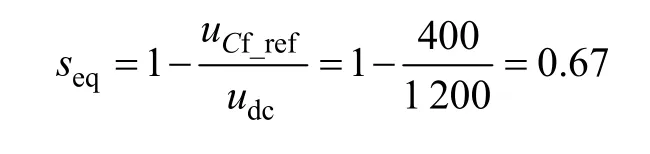
確定平衡點后，采用李雅普諾夫第二法對DC-DC混雜系統進行穩定性分析。系統李雅普諾夫函數可以表示為

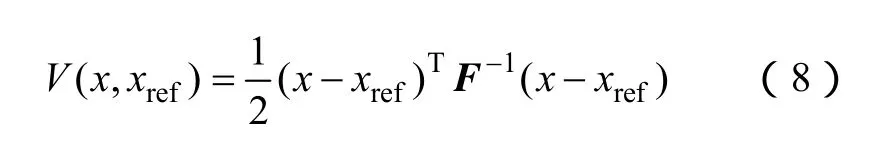
其導函數為

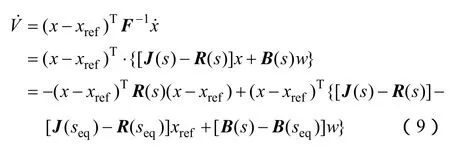
對于電力電子系統，可以選擇系統儲能元件（如電感、電容等）的能量和作為李雅普諾夫函數。在Boost電路中，系統的李雅普諾夫函數為

式中，iCf為流經電感的電流；uCf為超級電容的端電壓。由式（9）得式（10）的時間導數為

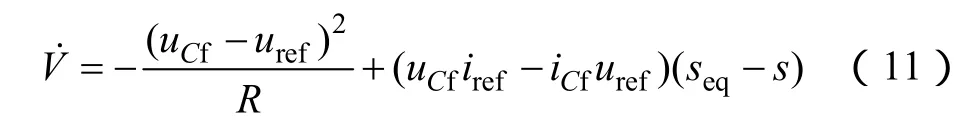
為了實現這一控制目標，這里引入一個滑模面方程，令P(x,t)=uCfiref-iCfuref，則控制策略可用下式描述。

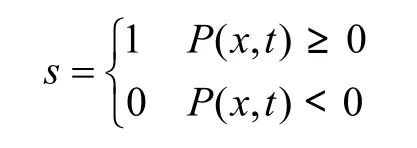
控制框圖如圖5所示。

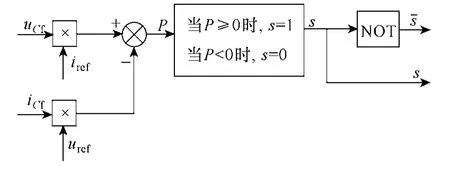
圖5 Boost電路的控制框圖Fig.5 The control diagram of Boost circuit

5 雙向DC-DC變換器的控制

5.1 基于超級電容器的DC-DC變換器的控制

基于超級電容器的雙向 DC-DC變換器電路[22]如圖6所示。

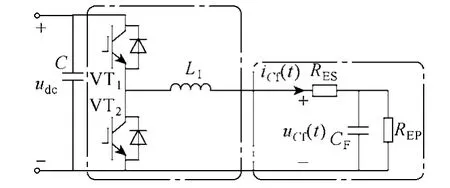
圖6 采用超級電容器的DC-DC電路Fig.6 DC-DC circuit with super capacity

雙向半橋 Buck-Boost電路的工作模式由直流母線兩端功率的平衡狀況決定。令發電機發出的功率為Ps，系統輸出的并網功率為Pg。穩態時，Ps與Pg近似相等，超級電容器不工作；當Ps＞Pg時，VT1觸發，DC-DC工作于 Buck電路狀態，超級電容器吸收能量；當Ps＜Pg時，VT2觸發，DC-DC工作于 Boost電路狀態，超級電容器釋放能量。在實際應用中，母線電壓和流經超級電容電流的變化作為功率變化的判據，圖 7為 DC-DC電路的控制框圖。

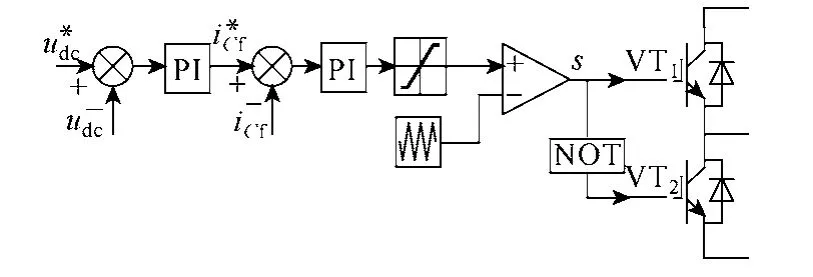
圖7 DC-DC電路的控制框圖Fig.7 The control diagram of the DC-DC circuit

5.2 加入類滑模控制的DC-DC變換器的控制

將類滑模控制加入到 DC-DC變換器的控制之后的框圖如圖8所示。

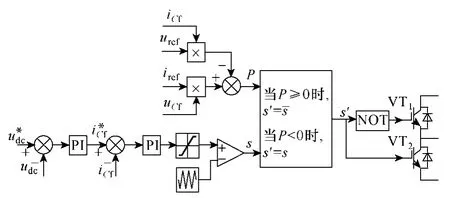
圖8 加入類滑模控制的DC-DC電路的控制框圖Fig.8 The control diagram of the DC-DC circuit with the sliding mode control

由圖 8可以看出，在雙向 DC-DC變換器電路中，類滑模控制的加入使系統除了滿足超級電容器充放電特性外，同時也滿足李雅普諾夫漸進性穩定的條件。基于混雜系統的類滑模控制沒有線性近似處理，理論上可以精確地控制 DC-DC變換器。另外，PI控制可以實現直流電壓的快速檢測和跟蹤，二者結合即可充分發揮超級電容器對直流母線電壓波動的抑制作用。

6 仿真分析

6.1 系統參數和仿真工況

在Matlab/Simulink環境下建立圖1所示風電系統的仿真模型，系統參數見下表。

通過采用三相電壓對稱跌落的方法，使低壓直流側母線電壓高于1 200V，此時DC-DC變換器工作于 Buck電路，系統將多余的電能儲存到超級電容器中。

通過采用瞬間減小風速的方法，使低壓直流側母線電壓低于1 200V，此時DC-DC變換器工作于Boost電路，超級電容器將儲存的電能釋放。

對比仿真類滑模控制接入前后風電系統的直流側電壓、超級電容器電壓和充放電電流的變化情況。

表 系統主要參數Tab. Parameters of wind power system

6.2 工作在Buck電路的工況

穩定運行的系統 1s到 1.625s時，并網點電壓跌落至0.2(pu)，1.625s時電壓開始逐漸恢復，2.5s時電壓恢復至0.9(pu)，仿真波形如圖9～圖11所示。

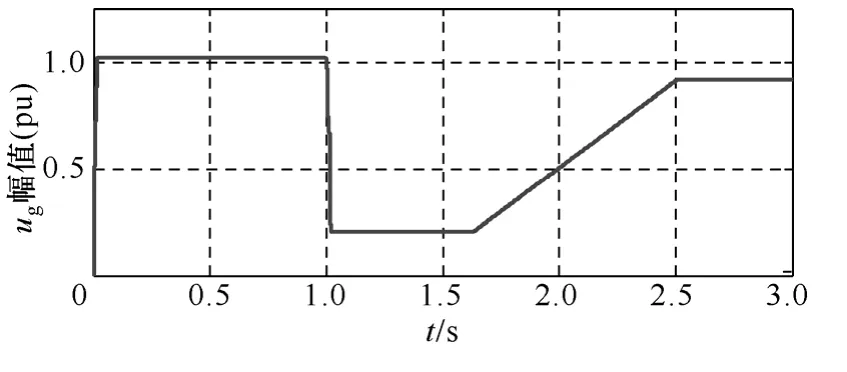
圖9 并網點電壓跌落幅值（a相）Fig.9 Grid voltage drop amplitude (phase a)

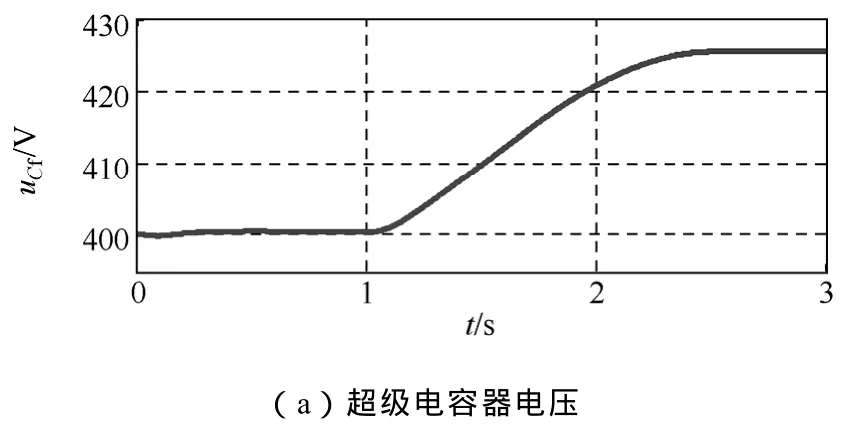
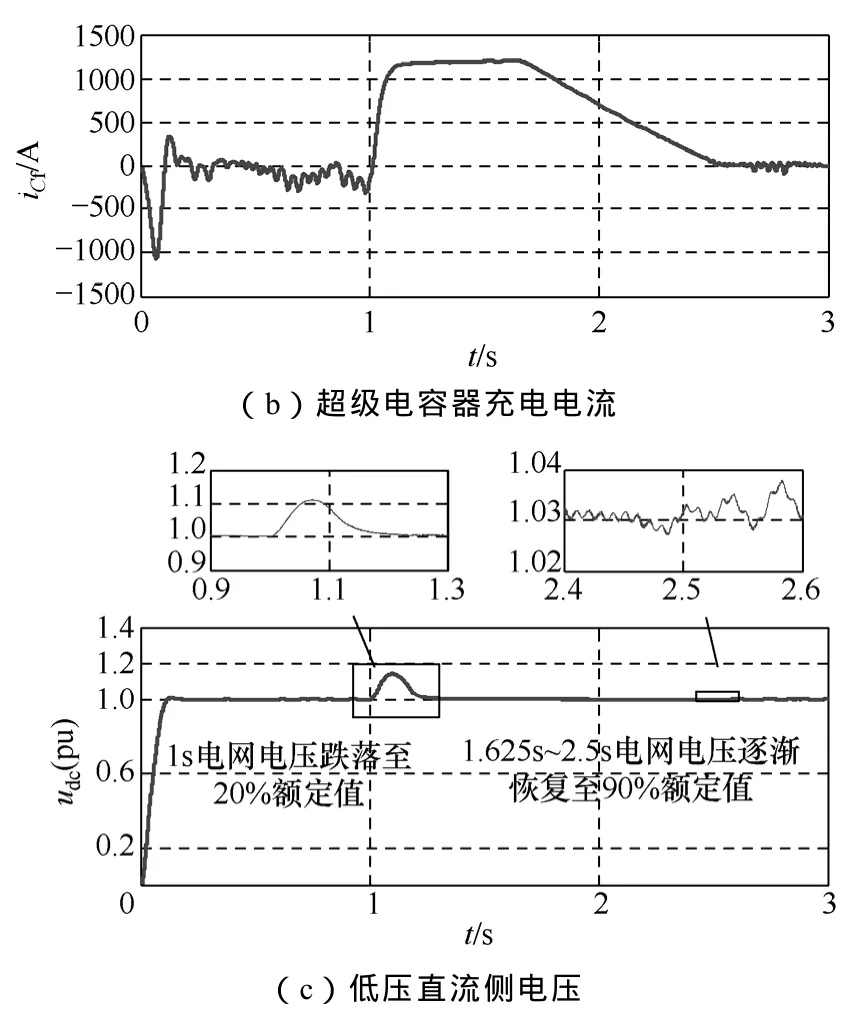
圖10 Buck電路中未加類滑模控制的仿真結果Fig.10 Simulation results of the Buck circuit without the sliding mode control

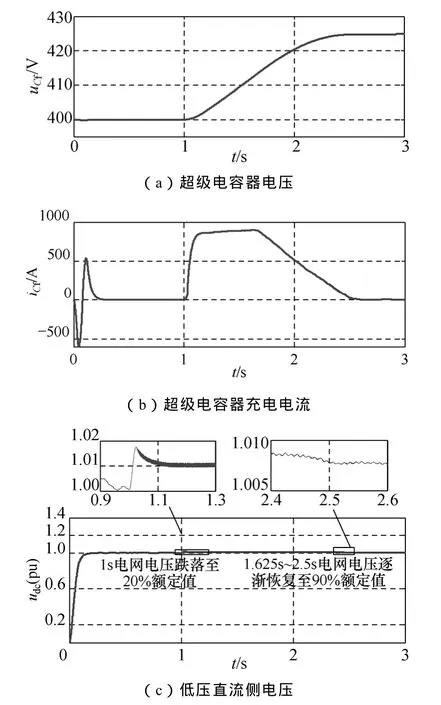
圖11 Buck電路中加入類滑模控制的仿真結果Fig.11 Simulation results of the Buck circuit with the sliding mode control

6.3 工作在Boost電路的工況

在 1s時風速由原來的 12m/s降低至 8m/s，2s后恢復到12m/s，仿真波形如圖12～圖14所示。

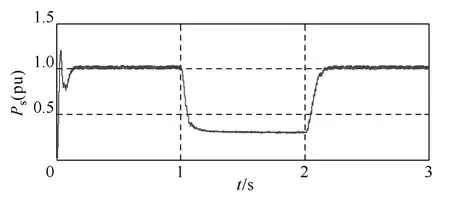
圖12 不同風速下的輸出功率Fig.12 Power output of different wind speeds

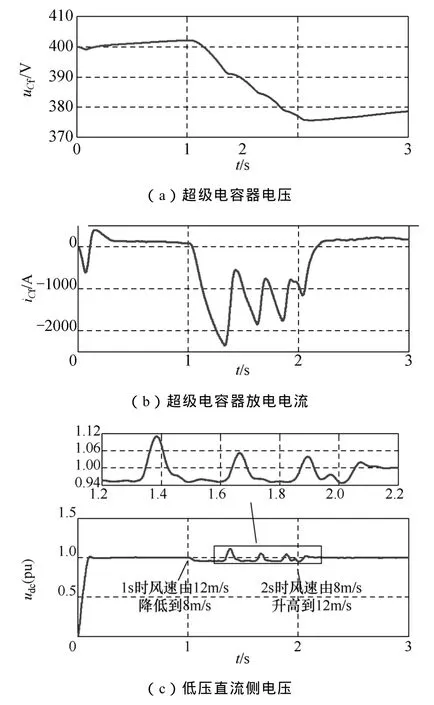
圖13 Boost電路中未加類滑模控制的仿真結果Fig.13 Simulation results of the Boost circuit without the sliding mode control

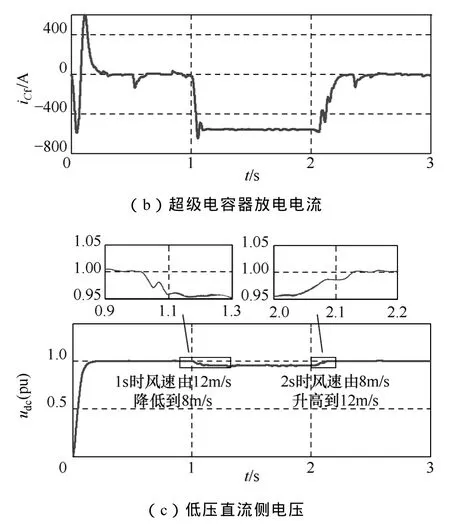
圖14 Boost電路中加入類滑模控制的仿真結果Fig.14 Simulation results of the Boost circuit with the sliding mode control

通過對波形進行對比，加了類滑模控制之后，直流母線電壓保持穩定，流經 DC-DC變換器的電流變小，有效地避免了電力電子器件過電流的情況。

7 結論

本文提出通過 DC-DC變換器控制超級電容充放電功率維持風電系統直流母線電壓穩定的控制策略，給出了 Boost電路混雜建模的李雅普諾夫穩定性條件，引入類滑模控制，實現了風電系統在大信號擾動時的電壓穩定。

混雜系統模型可以同時描述開關器件的離散特征和電氣量的連續性，在新能源并網系統的研究中有著廣闊的應用前景，值得進一步研究和討論。

[1] Lin Qihui,Wang Zhiming,Li Wangjie. Study on reactive power characteristics of doubly fed variable speed constant frequency wind power generator[C].Proceedings of International Conference on Electrical Machines and Systems,Piscataway,N J: ICEMS,2010: 547-552.

[2] 楊普,孫麗玲,吳娜,等. 并網型風力發電系統電壓穩定研究現狀[J]. 通信電源技術,2012,29(2):16-20.

Yang Pu,Sun Liling,Wu Na,et al. Updated research of voltage stability for grid-Connected wind power system[J]. Telecom Power Technologies,2012,29(2):16-20.

[3] PACS-L: SERC office. China’s wind power development survey report[EB/OL]. Beijing: State Electricity Regulatory Commission. 2009[2009-07-21].

[4] 李東東,陳陳. 風力發電系統動態仿真的風速模型[J]. 中國電機工程學報,2005,25(21): 41-44.

Li Dongdong,Chen Chen. Wind speed model for dynamic simulation of wind power generation system[J]. Proceedings of the CSEE,2005,25(21): 41-44.

[5] 張文亮,丘明,來小康. 儲能技術在電力系統中的應用[J]. 電網技術,2008,32(7): 1-9.

Zhang Wenliang,Qiu Ming,Lai Xiaokang. Application of energy storage technologies in power grids[J].Power System Technology,2008,32(7): 1-9.

[6] 趙海嶺,王維慶,王海云,等. 并網永磁直驅風電機組故障穿越能力仿真研究[J]. 電網與清潔能源,2010,26(7): 15-18.

Zhao Hailing,Wang Weiqing,Wang Haiyun,et al.Fault ride-through simulation of permanent magnetic synchronous generator connected into power grid[J].Advance of Power System & Hydroelectric Engineering,2010,26(7): 15-18.

[7] 張方華,朱成花,嚴仰光,等. 雙向 DC-DC變換器的控制模型[J]. 中國電機工程學報,2005,25(11):46-49.

Zhang Fanghua,Zhu Chenghua,Yan Yangguang,et al.The controlled model of bi-directional DC-DC converter[J]. Proceedings of the CSEE,2005,25(11): 46-49.

[8] 王云玲,曾杰,張步涵,等. 基于超級電容儲能系統的動態電壓調節器[J]. 電網技術,2007,31(8):58-61.

Wang Yunling,Zeng Jie,Zhang Buhan,et al. Dynamic voltage conditioner based on ultracapacitor energy storage system[J]. Power System Technology,2007,31(8): 58-61.

[9] 童亦斌,吳峒,金新民,等. 雙向DC/DC 變換器的拓撲研究[J]. 中國電機工程學報,2007,27(13): 81-86.Tong Yibin,Wu Tong,Jin Xinmin,et al. Study of bi-directional DC/DC converter[J]. Proceedings of the CSEE,2007,27(13): 81-86.

[10] Middlebrook R D,Cuk S. A general unified approach to modeling switching power converter stages[J].International Journal of Electronics,1977,42(6): 521-550.

[11] Middlebrook R D. Small-signal modeling of pulsewidth modulated switched-mode power converters[J].Proceedings of the IEEE,1988,76(4): 343-354.

[12] Cuk S,Middlebrook R D. A general unified approach to modeling switching DC-DC converters in discontinuous conduction mode[C]. IEEE PESC Record,1977: 36-37.

[13] 馬紅波,馮全源. Buck-Boost開關變換器的混雜建模與控制研究[C]. 2008全國博士生學術論壇—電氣工程論文集,2008: 926-936.

Ma Hongbo,Feng Quanyuan. Hybrid modeling and control for Buck-Boost switching converters[C]. 2008 Doctoral Forum of China-the Conference Proceeding of Electric Engineering,2008: 926-936.

[14] 馬皓,祁峰,張霓. 基于混雜系統的DC-DC變換器建模與控制[J]. 中國電機工程學報,2007,27(36):92-96.

Ma Hao,Qi Feng,Zhang Ni. Modeling and control for DC-DC converters based on hybrid system[J]. Proceedings of the CSEE,2007,27(36): 92-96.

[15] MOSSOBA J. T,KREIN PT. Exploration of Deadbeat Control for DC-DC converters as hybrid system[C].Proceedings of 36th IEEE Power Electronics Specialists Conference Brail: IEEE,2005; 1004-1010.

[16] 張明銳,劉金輝,金鑫. 應用于智能微網的 SVPWM固態變壓器研究[J]. 電工技術學報,2012,27(1):90-97.

Zhang Mingrui,Liu Jinhui,Jin Xin. Research on the SVPWM solid state transformer applied in smart micro-grid[J]. Transactions of China Electrotechnical Society,2012,27(1): 90-97.

[17] 荀海濤. 能量回收系統中超級電容電壓檢測與分析[D]. 上海: 同濟大學,2009.

[18] 張明銳,陳潔,王之馨,等. 一種新型的永磁同步風力發電機并網系統[J]. 電力系統保護與控制,2013,41(14): 141-148.

Zhang Mingrui,Chen Jie,Wang Zhixin,et al. A new permanent magnet synchronous wind-power generation grid-connected system[J]. Power System Protection and Control,2013,41(14): 141-148.

[19] 趙秀雅,王培紅. 超級電容儲能技術在可再生能源發電中的應用[C]. 第八屆長三角能源論壇—新形勢下長三角能源面臨的新挑戰和新對策論文集,2011: 168-171.

[20] 張步涵,曾杰,毛承雄,等. 串并聯型超級電容器儲能系統在風力發電中的應用[J]. 電力自動化設備,2008(4): 1-4.

Zhang Buhan,Zeng Jie,Mao Chengxiong,et al.Application of series-parallel energy storage system with super-capacitor in wind power generation[J].Electric Power Automation Equipment,2008(4): 1-4.

[21] Jean Buisson,Pierre Yves Richard,Herve Cormerais.On the stabilization of switching electrical power converters[C]. Proceedings of 8th International Workshop on Hybrid Systems: Computation and Control,2005.

[22] 侯世英,房勇,曾建興,等. 應用超級電容提高風電系統低電壓穿越能力[J]. 電機與控制學報,2010,14(5): 26-31.

Hou Shiying,Fang Yong,Zeng Jianxing,et al.Application of super capacitors to improve wind power system's low voltage ride through capability[J].Electric Machines and Control,2010,14(5): 26-31.