基于插入損耗的噪聲源阻抗修正計算方法

張佳佳 張逸成 韋 莉 葉尚斌 姚勇濤

（同濟大學電子與信息工程學院 上海 201804）

1 引言

隨著電力電子設備的不斷增多，電磁干擾（ElectroMagnetic Interference，EMI）問題越來越嚴重。根據(jù)耦合通路的不同，電磁干擾可分為傳導干擾和輻射干擾。抑制傳導干擾的主要途徑之一是使用EMI濾波器[1]。EMI濾波器的性能由插入損耗（Insertion Loss，IL）來表征，源阻抗和負載阻抗都會對插入損耗產生影響[2,3]。設計 EMI濾波器的基本流程可以概括為根據(jù)需實現(xiàn)的插入損耗目標，以及噪聲源阻抗和負載阻抗的特征，選擇合適的拓撲，確定差共模電感和電容的值[4,5]，并進行濾波元件的設計或選型及組合。

噪聲測試系統(tǒng)中的線性阻抗穩(wěn)定網絡（Linear Impedance Stabilization Network，LISN）為濾波器提供穩(wěn)定的純阻性阻抗[6]，即差模負載阻抗為100Ω，共模負載阻抗為25Ω。而噪聲源阻抗的相角和幅值都隨頻率而變化，并受較多因素影響[7]，因此需要通過測試的方式獲得源阻抗的信息。

源阻抗的測試方法包括：插入損耗法[8,9]、散射參數(shù)法[10]、單電流探頭法[11,12]和雙電流探頭法[13]等。其中，散射參數(shù)法、單電流探頭法和雙電流探頭法[14]對于測試設備要求都比較高，測試過程較為復雜[15]，并且測試準確度會因電流探頭的非理想傳輸特性而降低。插入損耗法的測試過程簡單，計算原理也易理解，在工程方面應用較多。但是，現(xiàn)有插入損耗法引入了一些假設條件作為簡化依據(jù)，在一些情況下，無法保證簡化計算的精度和可信性。

本文在分析傳統(tǒng)插入損耗法的基礎上，推導了精確的源阻抗幅值計算公式，實現(xiàn)全部數(shù)據(jù)點的準確計算，并對該方法進行了數(shù)學驗證。以電動汽車用 DC-DC變換器為測試對象，實現(xiàn)了源阻抗幅值的測試和計算，通過傳統(tǒng)方法和修正方法的計算結果對比，驗證了該方法的有效性和適用性。在此基礎上進行濾波元件的選型和濾波性能測試，證明修正方法可以避免過設計，有利于濾波元件的選型和設計，有助于濾波器體積和重量的優(yōu)化。

2 傳統(tǒng)電壓插入損耗法

2.1 差模噪聲源阻抗的傳統(tǒng)計算法

并聯(lián)電容可為差模噪聲提供通路。因此，測試差模噪聲源阻抗時，在噪聲源與負載（LISN）之間并聯(lián)插入電容，通過測試電容插入前后差模噪聲的變化比例（即電容的差模插入損耗），確定差模噪聲源阻抗的最大值和最小值。

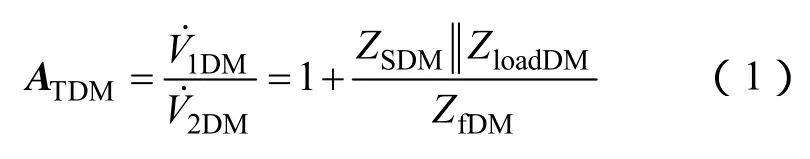
式中，ATDM可以通過測試獲得，ATDM=|ATDM|。

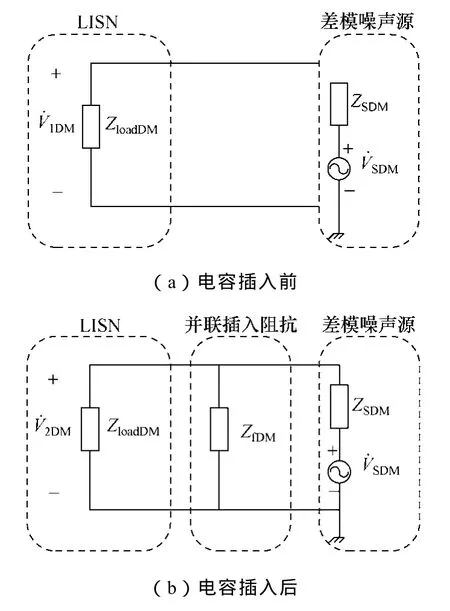
圖1 差模源阻抗測試等效電路Fig.1 Equivalent DM source impedance test equivalent circuit

若|ZSDM|<<|ZloadDM|=100，則上式可簡化為

記差模電容阻抗的實部和虛部分別為RfDM和XfDM，則式（2）的解軌跡[3]是以（–RfDM,–XfDM）為圓心，以ATDM|ZfDM|為半徑的圓。因此有

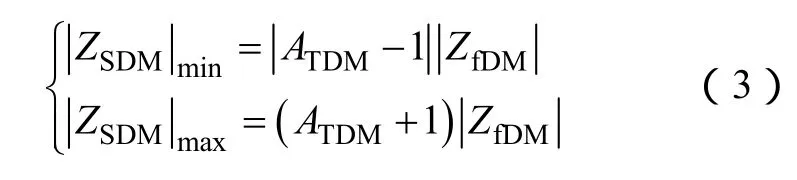
差模源阻抗的計算假設源阻抗遠小于負載阻抗100Ω。該假設條件限制了其使用范圍。后文的計算實例顯示，按傳統(tǒng)計算公式進行計算，得到的結果可能不滿足假設的前提，那么這樣的結果是無效的。

2.2 共模噪聲源阻抗的傳統(tǒng)計算法

共模噪聲源阻抗的測試方法與差模的情況類似。由于串聯(lián)電感為共模噪聲提供通路，因此在噪聲源與負載之間串聯(lián)插入電感。圖2a和圖2b分別是電感插入前后的測試等效電路，各參數(shù)的含義與差模情況一一對應，其中共模負載阻抗ZloadCM是穩(wěn)定的25Ω。

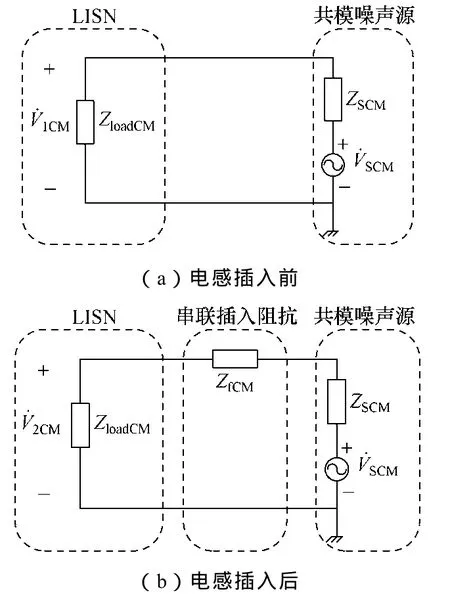
圖2 共模源阻抗測試等效電路Fig.2 Equivalent CM source impedance test equivalent circuit

串聯(lián)電感導致的電壓變化為

傳統(tǒng)的方法將式（4）移項取模，整理可得

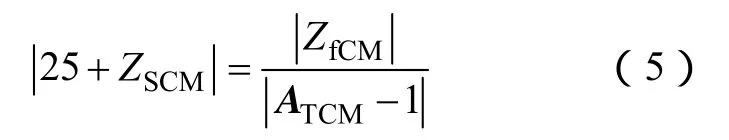
由于傳導噪聲發(fā)射測試只能獲得ATCM的幅值信息，式（5）等式右端的分母無法確定，因此文獻[3]采用了分段等效的方式進行計算。

當ATCM＞10時，將|ATCM-1|近似為ATCM。該式的解軌跡[3]是以（-25,0）為圓心，以|ZfCM|/ATCM為半徑的圓，因此共模源阻抗的最大值和最小值為

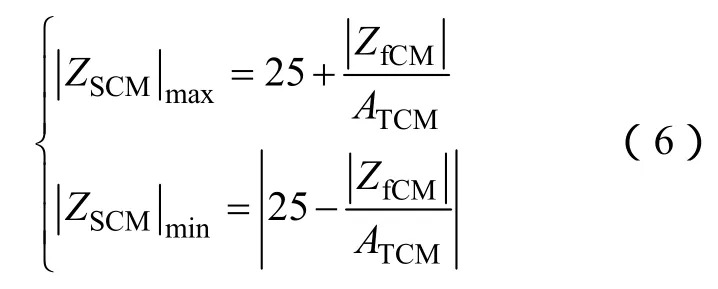
當ATCM＜10時，分別將|ATCM-1|近似為|ATCM-1|或ATCM+1，解軌跡[3]仍是圓，只是半徑的表達式有所改變，因此共模源阻抗最大值和最小值為

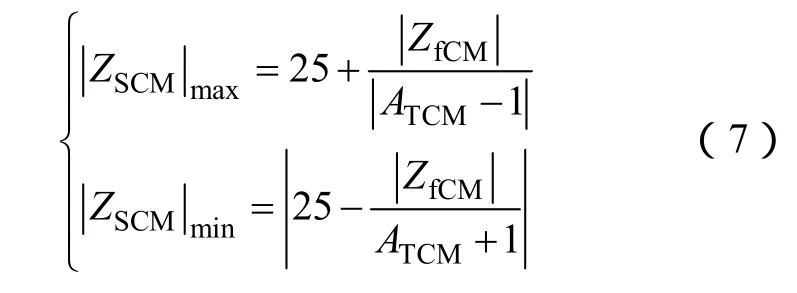
然而，這種假設近似在數(shù)學方面并不是嚴格成立的。當 0.1＜ATCM＜10，特別是ATCM實際值在 1附近時，這種近似會造成較大的誤差。為了說明該誤差，分別取|ATCM|為 0.8、0.9、1.1和1.2，ATCM的相角α取為 0°、90°、180°和270°，計算|ATCM-1|、|ATCM-1|和ATCM+1，計算結果見表1。

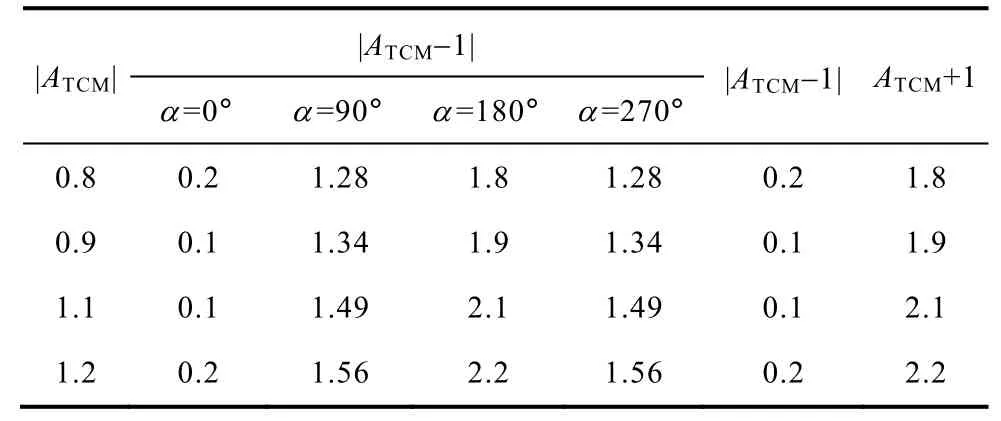
表1 |ATCM-1|近似導致的誤差Tab.1 Errors caused by |ATCM-1| approximation

從表1中可以看出，近似計算是將|ATCM-1|的范圍擴大。盡管這種近似計算的絕對誤差很小，但是相對誤差可能很大，進而導致源阻抗的計算誤差。以|ATCM|=0.9，α=90°為例，兩種近似的相對誤差分別為-92.54%和41.79%，故ZSCMmax的絕對誤差為0.925|ZfCM|/(0.9×0.075)=13.7|ZfCM|，ZSCMmin絕對誤差為 0.418|ZfCM|/(0.9×1.418)=0.33|ZfCM|。|ZfCM|一般較大，因此將導致很大的源阻抗幅值計算誤差。為了評估絕對誤差的等級，將表1中各情況下源阻抗最大值和最小值的誤差與|ZfCM|的比值，即絕對誤差系數(shù)，分別進行計算，結果列于表2。從表2的數(shù)據(jù)可以發(fā)現(xiàn)，當 0.1＜ATCM＜10，特別是ATCM實際值在1附近時，兩種近似計算會分別導致共模源阻抗最大值和最小值的誤差。

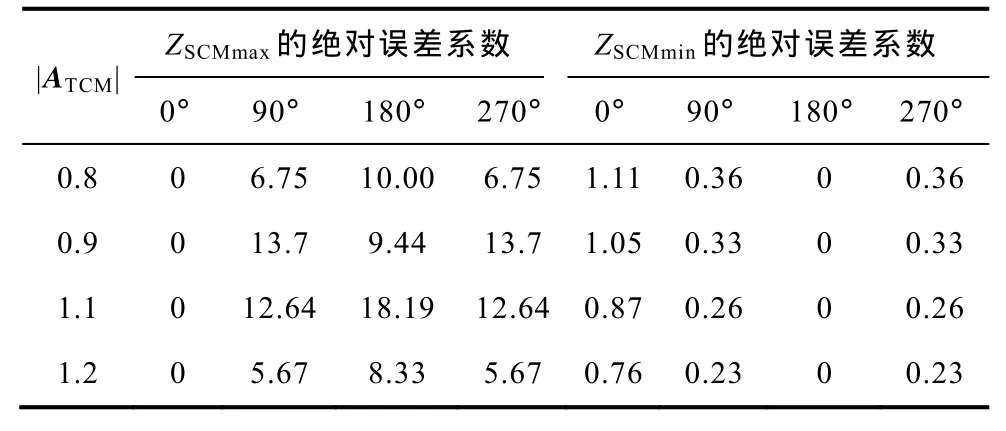
表2 兩種近似導致的ZSCMmax和ZSCMmin誤差Tab.2ZSCMmaxandZSCMminerror by approximation

3 修正的電壓插入損耗法

3.1 差模噪聲源阻抗的修正計算

由于傳統(tǒng)計算差模源阻抗的方法采用近似假設，在應用中受到約束，因此采用精確解析法，取消假設條件對公式適用范圍的限定。推算過程如下。

將差模源阻抗和并聯(lián)電容阻抗均表示為電阻和電抗組合的形式，代入基本等式（1）中，并將右端分式進行整理，可得到簡化表達為

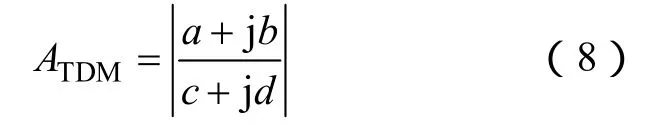
其中，過渡變量分別為

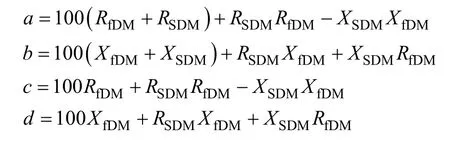
將簡化表達式（8）兩端平方去除模，整理后得

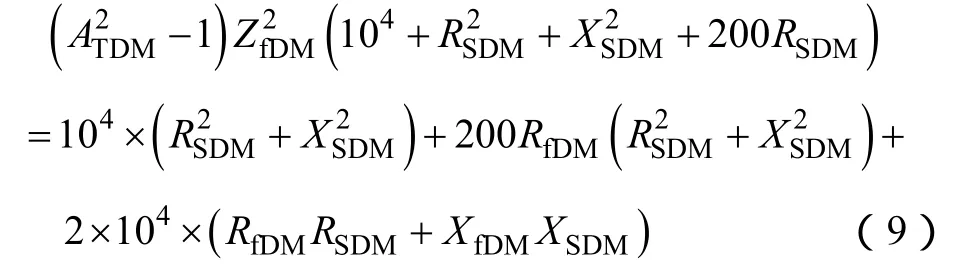
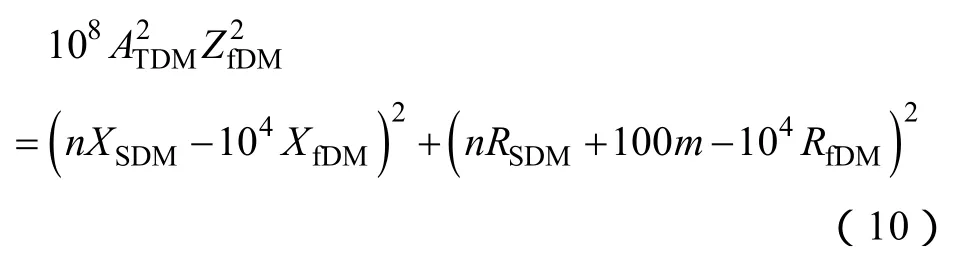
式（10）的解軌跡是圓。圓心的橫坐標x0DM為(104RfDM-100m)/n，縱坐標y0DM為 104XfDM/n，半徑rDM為104ATDM|ZfDM|/n。因此，差模源阻抗的最大值和最小值為

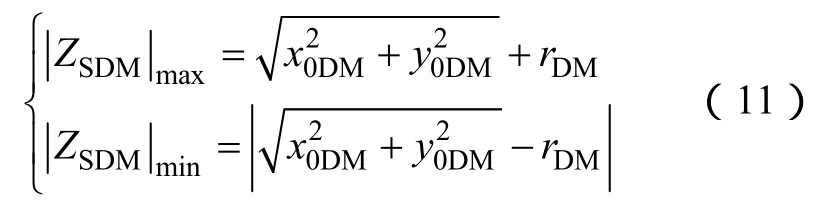
為了驗證推導的解析結果的正確性，進行數(shù)學驗證。根據(jù)式（8）的解軌跡特征，可以寫出解軌跡中任意一點的坐標為

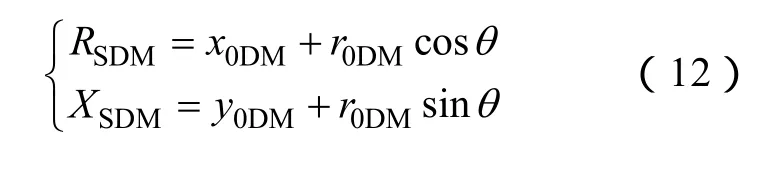
將式（12）代入原始計算式（1）中，等式恒成立。因此，用改進的源阻抗計算法得到的解析結果是正確的。這種求解的方式不包含化簡假設，在差模噪聲源阻抗為任意值情況下都成立。

3.2 共模噪聲源阻抗的修正計算

將電感阻抗和共模源阻抗均表示為電阻和電抗的形式，代入原始計算式（4）并取模得

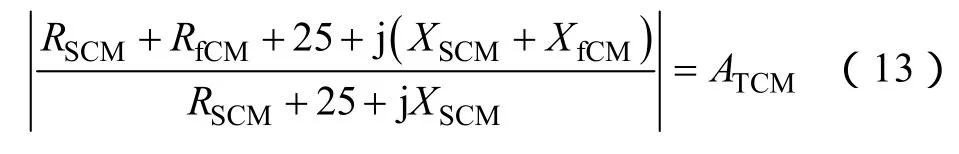
式（13）的解軌跡是到點（-25-RfCM,-XfCM）和（-25,0）距離之比為ATCM的點軌跡，即阿波羅尼斯圓。將式（13）兩端進行平方展開，整理后得

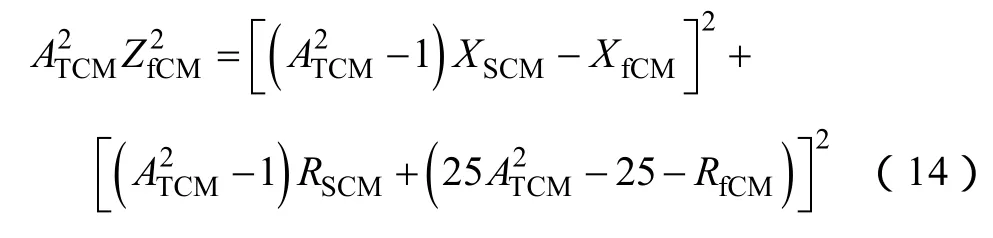
因此，式（14）解軌跡的圓心橫縱坐標分別為x0CM=-25+RfCM/()，y0CM=XfCM/()，半徑rCM=ATCM|ZfCM|/||。

相應地，共模源阻抗的最大值和最小值為

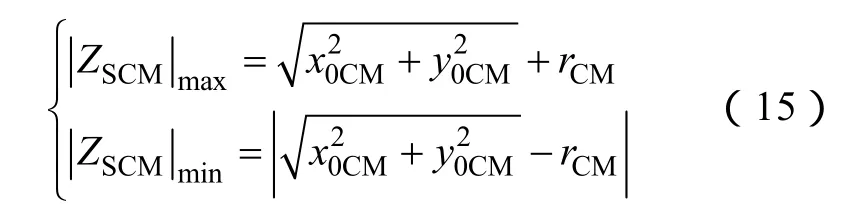
該公式的驗證方法與差模源阻抗修正計算公式的驗證方法一致，文中不再贅述。

4 測試實例與結果分析

4.1 測試平臺及測試數(shù)據(jù)

以電動汽車用DC-DC變換器為研究對象，按照汽車級零部件傳導發(fā)射測試標準[16]的要求，布置如圖3所示的傳導發(fā)射測試平臺。在測試中，DC-DC變換器輸入電壓為12V，由蓄電池供電；輸出功率為60W。在蓄電池與待測端口間，使用FCC 25A等級LISN；LISN的信號端通過端阻抗為50Ω的同軸電纜與EMCIS EA2100差/共模分離儀相連；分離出的噪聲送入Agilent E7402A EMI接收機進行分析。

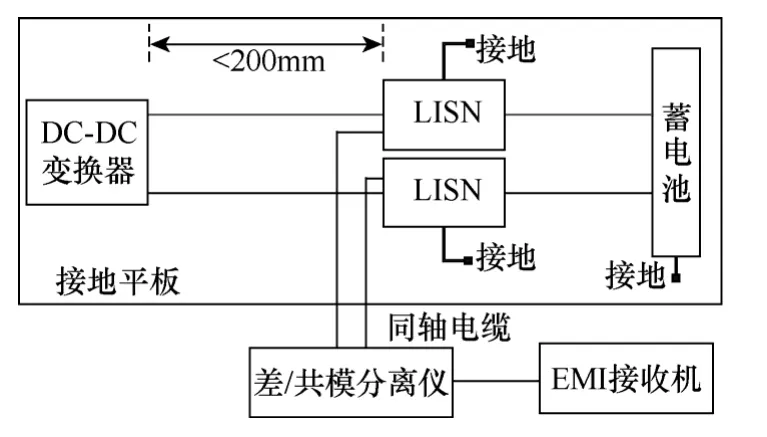
圖3 傳導發(fā)射測試平臺Fig.3 Conducted emission test bench

利用圖3的平臺，測試電容、電感插入前后的噪聲頻譜，計算電壓幅值變化，結果如圖4和圖5所示。插入電容為標稱1nF的電容，插入電感為Coilcraft Q4018-A共模扼流圈。二者的阻抗均通過 Agilent 4395A阻抗分析儀測試獲得。

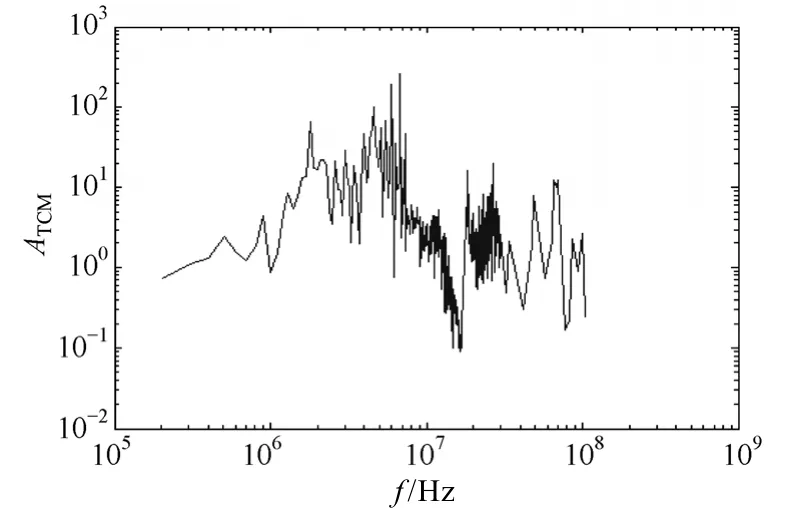
圖5 插入電感導致的共模電壓幅值變化比例Fig.5 Change ratio of CM voltage amplitude caused by inductor insertion

4.2 差/共模噪聲源阻抗計算

根據(jù)圖4的結果和插入電容阻抗的測試數(shù)據(jù)，分別按照式（3）和式（11）兩種方法，計算差模源阻抗的最大值和最小值，結果如圖6所示。其中，虛線為傳統(tǒng)方法的結果，實線為修正方法的結果。

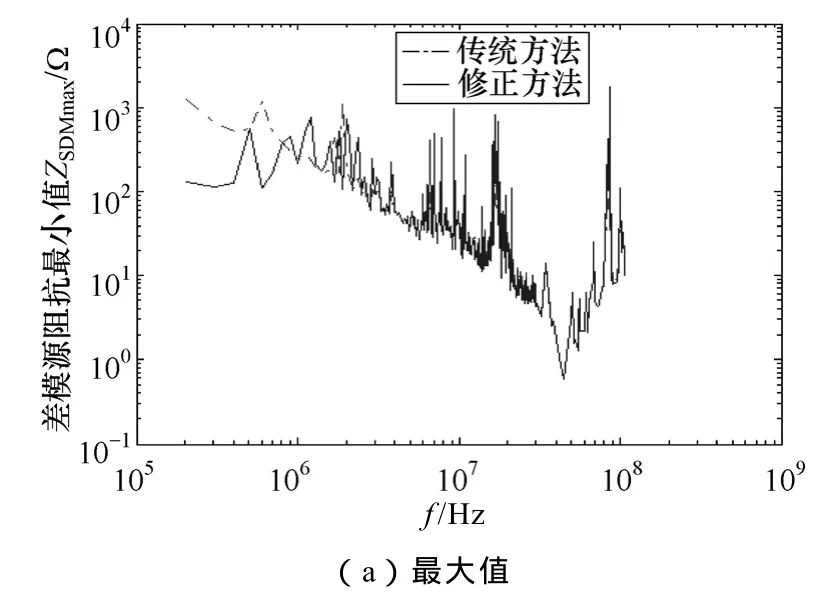
圖6 差模源阻抗計算結果Fig.6 The calculated DM source impedance

從圖6a和圖6b可以看出，在許多頻段，傳統(tǒng)方法得到的差模源阻抗都在 100Ω及以上等級，不滿足假設條件，這些頻段的傳統(tǒng)方法的結果是無效的。表3列出了部分無效頻段傳統(tǒng)方法和修正方法的計算結果及傳統(tǒng)方法的相對誤差。從中可以發(fā)現(xiàn)，在這些無效的頻段，差模源阻抗的最大值和最小值均有較大誤差，最大相對誤差可達1個數(shù)量級。

表3 傳統(tǒng)法與修正法的ZSDM最大/最小值結果對比Tab.3ZSDMmax/ZSDMminresult comparison between conventional method and corrected method

類似地，根據(jù)圖5和插入電感阻抗的測試數(shù)據(jù)，分別按照式（6）、式（7）和式（15）計算共模源阻抗的最大值和最小值，結果如圖7所示。其中，虛線為傳統(tǒng)方法的計算結果，實線為修正方法的計算結果。

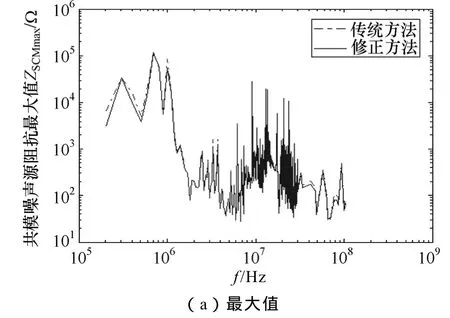
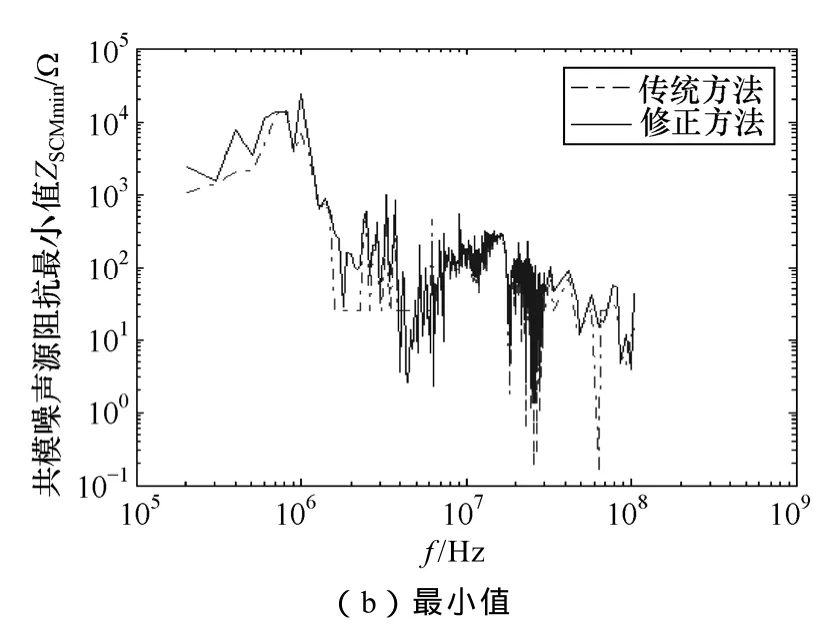
圖7 共模源阻抗計算結果Fig.7 The calculated CM source impedance

圖7中，共模源阻抗結果在低頻段的誤差相對較大，這是由于該頻段的|ATCM|接近于1。為了定量分析誤差，將低頻段頻段傳統(tǒng)法和修正法的結果及相對誤差列于表4。其中，205kHz的誤差最明顯，最大值的相對誤差為107.2%，最小值的相對誤差為-52.91%。一般而言，需要根據(jù)共模噪聲源阻抗的范圍和轉折頻率需求確定共模電感量。因此，若根據(jù)表4中傳統(tǒng)方法的計算結果對共模扼流圈進行設計或選型，那么將導致近1倍的過設計。

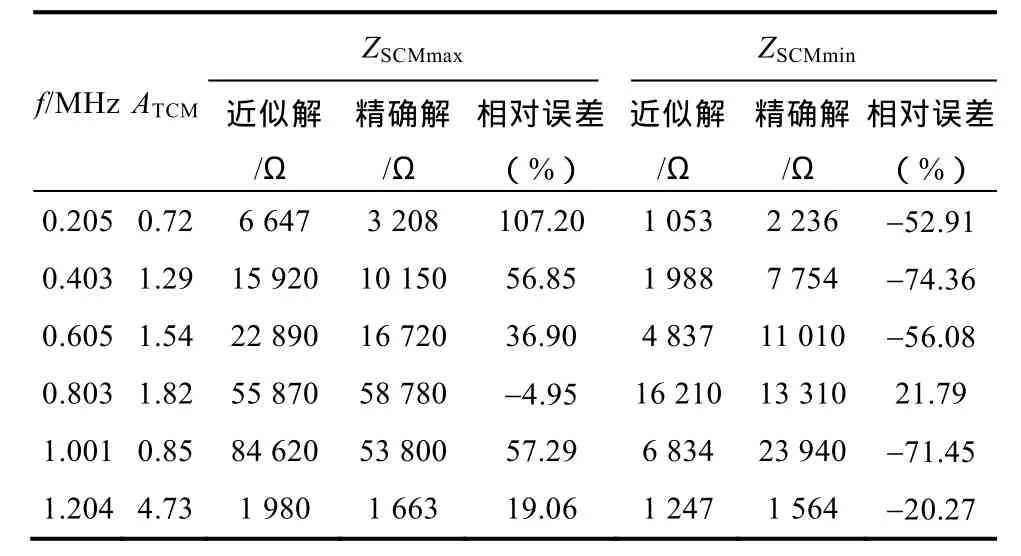
表4 傳統(tǒng)法與修正法的ZSCM最大/最小值結果對比Tab.4ZSCMmax/ZSCMminresults comparison between conventional method and corrected method

4.3 濾波元件選型及性能測試

為進一步說明過設計的影響，進行濾波元件選型和性能分析。差共模源阻抗范圍分別如圖 6和7所示，原始噪聲為圖3所示平臺測得的未插入電容和電感情況下的噪聲，噪聲頻率和限值設計目標為汽車級零部件傳導噪聲Level III級，在確定需實現(xiàn)的差共模插入損耗目標時增加6dB的裕量。

濾波器設計的主要依據(jù)有兩項：一是通過測試獲得的差共模源阻抗范圍；二是根據(jù)需實現(xiàn)的插入損耗確定的濾波器最大轉折頻率。根據(jù)源阻抗和負載阻抗的數(shù)量級，選擇圖8的單級濾波結構。根據(jù)阻抗失配的原則，綜合轉折頻率的限值，共模參數(shù)應滿足：①共模電感的阻抗應遠大于共模噪聲源阻抗（工程應用中取2倍以上）；②諧振頻率不高于轉折頻率的設計目標。因此，若共模源阻抗的測試結果偏大，那么所需的共模電感量也相應地增大。差模電感和電容的計算與此類似。表5列出了根據(jù)兩種方法計算結果確定的濾波參數(shù)最小值。

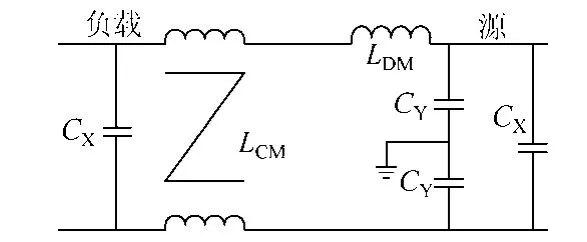
圖8 濾波結構Fig.8 Filter structure

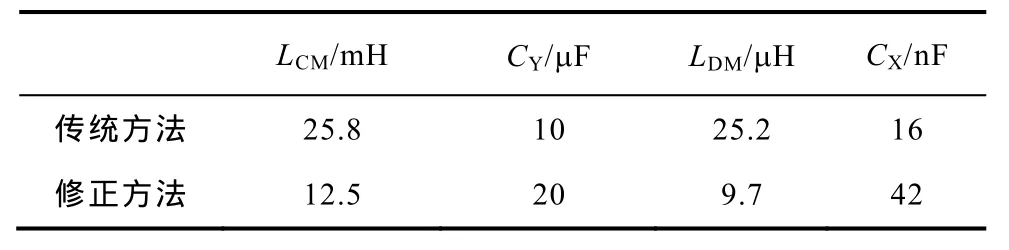
表5 傳統(tǒng)法與修正法的濾波參數(shù)計算結果Tab.5 Calculation results of filter parameters between conventional method and corrected method

根據(jù)表5的結果，共模電容均選擇Muruta公司的22μF電容，差模電容均選擇Muruta公司的0.1μF電容。兩種方法所需要的差模電感量均可降低為4.1μH，而共模電感量主要由共模源阻抗決定，所以仍按照表5中的結果進行選型。考慮到電流裕量問題，從Coilcraft公司9A等級的扼流圈中進行選型，無法找到滿足傳統(tǒng)方法需要的扼流圈，而根據(jù)修正方法的結果選擇CMT4-17-9L型號扼流圈。該款扼流圈的共模感量為 17mH，差模漏感為 220μH。根據(jù)選好的扼流圈和電容制成濾波器，安裝在 DC-DC變換器電源輸入端，測試濾波器加裝前后的正線噪聲，結果如圖9所示。從中可以看出，按照修正方法結果進行選型制作的濾波器，除 200kHz處外，在10MHz以下均能保證30dB以上的插入損耗，部分頻點（如500kHz）甚至能達到60dB的噪聲衰減。

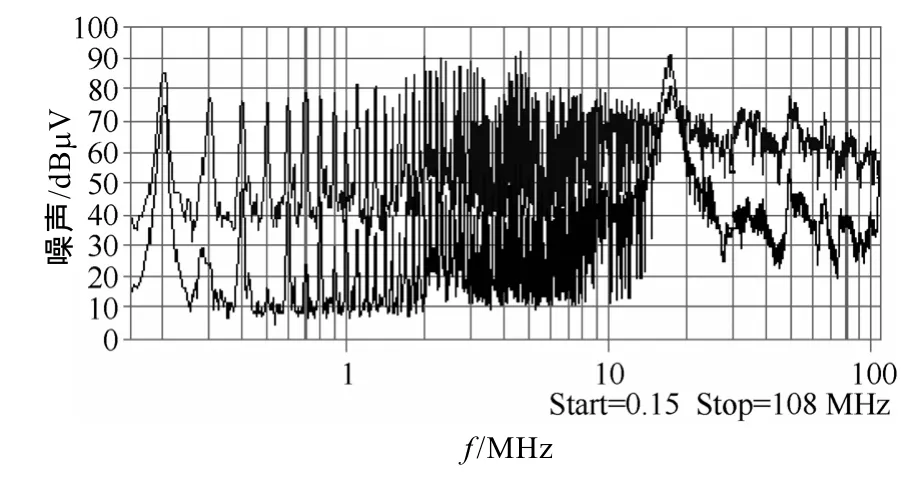
圖9 濾波器加裝前后的正線傳導噪聲測試結果Fig.9 Conducted noise of power line measured with and without the filter

圖9的結果說明，按照修正計算結果選擇器件制成的濾波器可以實現(xiàn)期望的插入損耗。因此，傳統(tǒng)方法所得出的器件參數(shù)，特別是共模電感量需求，處于過設計的狀態(tài)，這也正是無法進行共模扼流圈選型的原因。

若自行設計制作共模扼流圈，那么根據(jù)表5中共模電感量的計算結果，修正計算方法所需的共模電感量僅為傳統(tǒng)方法的一半。若選擇相同的磁心材料，那么修正方法所需的扼流圈的匝數(shù)也為傳統(tǒng)方法的一半，相應的窗口面積也可以減小，扼流圈的體積和重量得以降低。此外，由于傳統(tǒng)方法所需的匝數(shù)較多，在大電流應用場合，扼流圈的繞制和散熱設計都十分困難。

5 結論

傳統(tǒng)的電壓插入損耗法需要在一定的假設條件下，對源阻抗的幅值范圍進行近似計算，適用范圍較窄。本文對計算方法進行了修正，去除假設條件的約束，推導源阻抗幅值的精確解析表達式，經過數(shù)學驗證推導結果成立，其精確解析結果適用于實際電壓變化比例和源阻抗幅值為任意值的情況。

通過對 DC-DC變換器源阻抗的測試與計算分析發(fā)現(xiàn)：差模情況下，部分頻段傳統(tǒng)方法的結果無效，且與修正方法得到的精確解析結果相差近1個數(shù)量級；共模情況下，當插入電感導致的電壓變化比例在 0.1～10之間時，傳統(tǒng)方法與修正方法的結果相差較大，傳統(tǒng)方法的近似結果相對于修正的精確結果的最大相對誤差可達 100%以上，由此可能導致共模扼流圈近1倍的過設計。計算結果的對比證明了修正方法的有效性和準確性優(yōu)勢。濾波元件選型和濾波性能測試結果進一步證明，修正方法避免了過設計，為濾波元件的選型和設計提供了便利，并有助于濾波器體積、重量等的優(yōu)化。

[1] 石磊磊,王世山,徐晨琛. 二端口網絡散射參數(shù)理論及其在平面EMI濾波器測試中的應用[J]. 電工技術學報,2013,28(2): 78-85.

Shi Leilei,Wang Shishan,Xu Chenchen. Theory of scatter parameters of two port network and its application in the test of planar EMI filter[J]. Transactions of China Electrotechnical Society,2013,28(2): 78-85.

[2] Vuttipon Tarateeraseth. EMI filter design Part III:selection of filter topology for optimal performance[J].IEEE Electromagnetic Compatibility Magazine,2012,1(2): 60-73.

[3] Sheng Y,Eberle W,Liu Y. A novel EMI filter design method for switching power supply[J]. IEEE Transactions on Power Electronics,2004,19(6): 1668-1678.

[4] 王世山,朱葉,石磊磊. 基于環(huán)形感容集成結構單元的平面EMI濾波器設計理論及實施[J]. 電工技術學報,2013,28(1): 126-135.

Wang Shishan,Zhu Ye,Shi Leilei. Design theory and implementation of planar EMI filter based on annular integrated inductor-capacitor unit[J]. Transactions of China Electrotechnical Society,2013,28(1): 126-135.

[5] 溫志偉,伍曉峰,徐德鴻,等. 集成 EMI濾波器原理與設計[J]. 電工技術學報,2011,26(9): 160-166.

Wen Zhiwei,Wu Xiaofeng,Xu Dehong,et al. Principles and design on Integrated EMI filter[J]. Transactions of China Electrotechnical Society,2011,26(9): 160-166.

[6] International Special Committee on Radio Interference. CISPR 16-1-2: 2006 Specification for radio disturbance and immunity measuring apparatus and methods-Part1-2: Radio disturbance and immunity measuring apparatus Ancillary equipment- Conducted disturbances[S]. 2006.

[7] Liu Q,Wang S,Wang F,et al. EMI suppression in voltage source converters by utilizing DC-link decoupling capacitors[J]. IEEE Transactions on Power Electronics,2007,22(4): 1417-1428.

[8] Zhang D,Chen D Y,Nave M J,et al. Measurement of noise source impedance of off-line converters[J]. IEEE Transactions on Power Electronics,2000,15(5): 820-825.

[9] Meng J,Ma W,Pan Q,et al. Identification of essential coupling path models for conducted EMI prediction in switching power converters[J]. IEEE Transactions on Power Electronic,2006,21(6): 1795- 1803.

[10] Hu B,See K Y,Richard W C. Evaluation of ferrite core EMI suppression under realistic working conditions[C]. The 19th International Symposium on EMC,Zurich,Switzerland,2008: 774-777.

[11] Qiu X,Zhao Y,See K Y,et al. An efficient noise source impedance estimation approach applied in electromagnetic compatibility[J]. Chinese Journal of Electronics,2009,18(4): 744-748.

[12] Zhao Yang,Lu Xiaoquan,Dong Yinghua,et al. Study on impedance extraction methods applied in conductive EMI source modeling[C]. Asia Pacific International Symposium on Electromagnetic Compatibitity,Beijing,China,2010: 998-1001.

[13] Vuttipon Tarateeraseth. EMI filter design Part II:measurement of noise source impedances[J]. IEEE Electromagnetic Compatibility Magzine,2012,1(1):42-49.

[14] See K Y,Deng J. Measurement of noise source impedance of SMPS using a two probes approach[J].IEEE Transactions on Power Electronics,2004,19(3):862-868.

[15] Zhao B,Zhao M,Feng Z,et al. Standard resistor calibration method in measurement of noise source impedance using dual-probe approach[C]. CEEM,Xi’an,China,2009: 408-411.

[16] CISPR 25-2002: Radio disturbance characteristics for the protection of receivers used on board vehicles boats and on devices-limits and methods of measurements[S]. 2002.