基于Hilbert-Huang變換的1 000kV輸電線路雷電繞擊與反擊識別方法

羅日成 李 穩 陸 毅 黃 彪 胡宗宇

（1. 長沙理工大學電氣與信息工程學院 長沙 410004 2. 國電永福發電有限公司 桂林 541805 3. 國網岳陽供電公司 岳陽 414000 4. 國網益陽供電公司 益陽 413000）

1 引言

前蘇聯和日本為了防護雷電過電壓，都對特高壓架空輸電線路作了精心的防雷設計。盡管國外在特高壓線路設計時認為特高壓架空輸電線路耐雷水平很高，但運行后仍多次發生雷擊跳閘事故[1]。前蘇聯1 150kV特高壓線路在6年的運行時間內發生雷擊跳閘 21次，跳閘率高達 0.7次/（km·a）。特高壓輸電線路一般長達數百公里，由于受到輸電走廊的地形、氣候等因素的影響，極易遭受雷擊，從而產生過電壓，造成絕緣子閃絡，引起跳閘停電[2]。研究表明，雷擊是造成輸電線路跳閘的主要原因，它又分為繞擊和反擊兩種[3,4]。繞擊和反擊的機理及過程不同，防護措施也不同。若對線路雷擊方式進行有效識別，就能給線路安全運行及防雷工作提供正確的指導，給防雷措施的制定提供理論依據。

先導發展法從氣體放電的物理過程出發，先導的發展速度與加在絕緣子串兩端的瞬時電壓和先導發展長度有關，通過計算先導發展長度來判斷是否閃絡，理論上適用于任何波形，能直觀、合理地描述絕緣擊穿過程[5]。同時，研究發現對于500kV及以上的輸電線路，由于桿塔高度的增加，雷電波在桿塔及線路中的折、反射作用對于桿塔節點電位變化的影響很大，且最終影響線路雷電過電壓[6-8]，所以將先導發展模型應用于輸電線路雷電繞擊與反擊的識別，更符合實際情況，且克服了電氣幾何模型對識別結果的影響。

本文首先在考慮雷電先導發展過程的基礎上，利用ATP-EMTP軟件建立了1 000kV輸電線路雷電繞擊與反擊的仿真模型，然后運用Matlab軟件對仿真數據進行分析，采用HHT方法來提取特高壓線路中雷電過電壓信號的特征量，并計算其方差貢獻率，以此判斷繞擊與反擊。本文首次將希爾伯特-黃變換應用于特高壓輸電線路雷電繞擊與反擊識別，克服了傅里葉算法和Prony算法難以處理非平穩信號的缺點，并規避了小波算法中小波基難以選取的問題[9]，能夠從非平穩的高頻振蕩信號中準確提取動態振蕩特性以及豐富的系統故障暫態信息。實測技術中采用磁帶、磁鋼棒等方法通過測量雷電流波形參數來進行繞擊與反擊的識別，由于此類裝置不能重復測量，數據獲取工作量大，依靠工作經驗來判別，容易出現誤判[9]。本文所提出的雷電繞擊與反擊識別方法只需通過變電站錄波裝置記錄的雷電過電壓信號即可對雷擊方式進行準確識別。仿真及實測數據驗證結果表明：本文方法能為1 000kV輸電線路防雷的分析和設計提供理論參考。

2 輸電線路雷電暫態仿真模型

2.1 先導法模型

先導發展是長間隙放電的特有現象，本文用非線性電感模型模擬雷電先導發展的長間隙放電。它是一種高精度、長間隙放電的先導法模型，能夠模擬放電前驅電流的發展過程。非線性電感模型依據外加電壓到達間隙的臨界放電電壓為先導開始條件，只要放電時間不是特別短，先導開始時間對模擬精度的影響不大。非線性電感模型的電路如圖 1所示[11]。

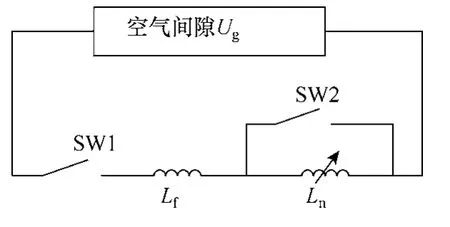
圖1 先導發展的非線性電感模型Fig.1 Nonlinear inductance model

圖 1中，Ln是放電間隙的等值非線性電感，以φn-i的形式給出其值。Lf表示閃絡后穩態電弧的等值線性電感。SW1表示先導發展開始的開關，當間隙電壓達到先導開始電壓Vm時閉合。SW2表示閃絡的開關，當間隙電流達到閃絡電流if時或者間隙電壓為零時閉合。上述相關參數的計算方法[11]為

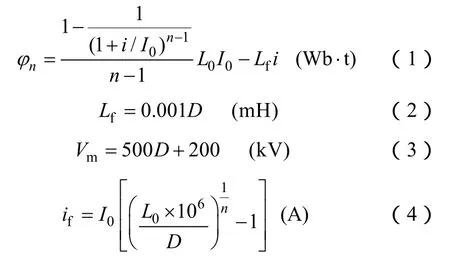
式中，D為間隙長，m；L0為小電流領域的等值電感；n為大電流領域的等值電感-電流特性的斜率；I0為等值電感為L02n時的電流，即拐點電流；Vm為先導開始電壓；if為閃絡電流。

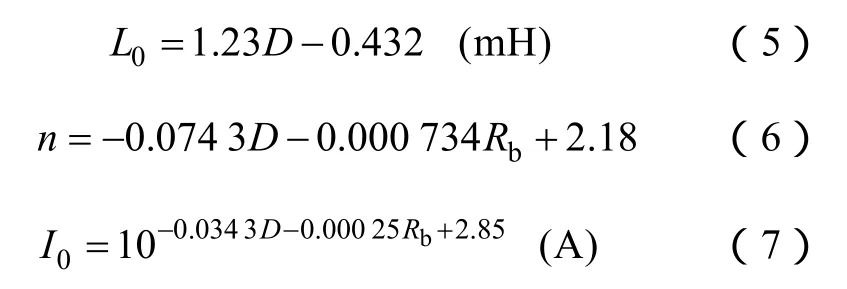
式中，Rb是從間隙等效得到的系統等值阻抗，可在閃絡點插入 1A電流源后計算得到，也可取 100～300Ω范圍內的值，此值對計算結果的影響不大。式（1）～式（7）中相關參數的取值和適用條件，讀者可參閱文獻[11]，此處不再贅述。

2.2 鐵塔模型

1994年Yamada和Ishii[12]用直測法對特高壓塔進行了測量，提出了基于EMTP的多層傳輸塔模型。將鐵塔分成四段，用無損線路和R-L并聯電路的串接來模擬鐵塔，Rf為塔腳接地電阻，如圖 2所示。

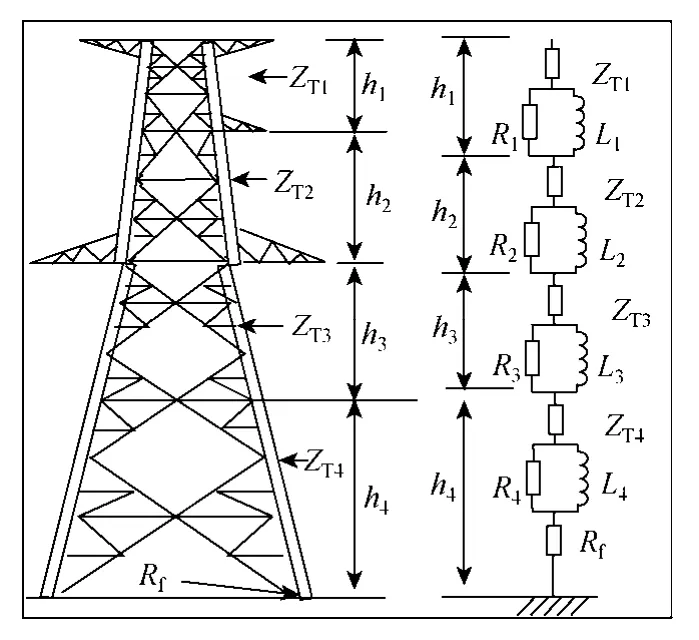
圖2 多層傳輸塔模型Fig.2 Multistory transmission tower model

鐵塔分段模型中各段中的阻尼電阻Ri和阻尼電感Li根據文獻[12]中給出的公式來計算。

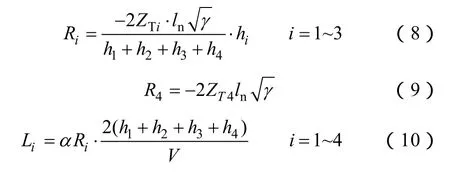
式中，hi各段相應的長度；ZTi為鐵塔波阻抗；γ為鐵塔整體的衰減系數；V為沖擊波在鐵塔中的傳播速度；α為阻尼系數。文中參數取值按文獻[12]：ZTi=120Ω（i=1～4），γ=0.7，V=300m/μs，α=1。

3 輸電線路的雷電過電壓電磁暫態仿真

3.1 仿真條件

利用ATP-EMTP以1 000kV線路為例，建立了考慮先導發展的過程仿真模型，研究雷電繞擊與反擊的暫態特性。仿真中雷電流模型為2.6/50μs的雙指數波；根據 DL/T620—1997，文中雷電流對應的雷電通道波阻抗取400Ω；絕緣子串采用考慮先導發展的非線性電感模型；桿塔采用多層傳輸塔模型，接地電阻為10Ω；線路采用JMarti·模型且考慮了沖擊電暈的影響[13]。仿真模型如圖3所示。

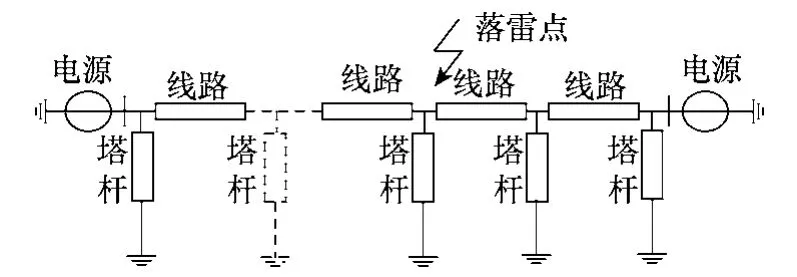
圖3 輸電線路模型Fig.3 Transmission line model

3.2 先導發展對雷電過電壓的影響

基于本文所搭建的考慮了先導發展的雷電過電壓仿真模型，研究反擊時先導發展對線路過電壓的影響。仿真結果如圖4所示。

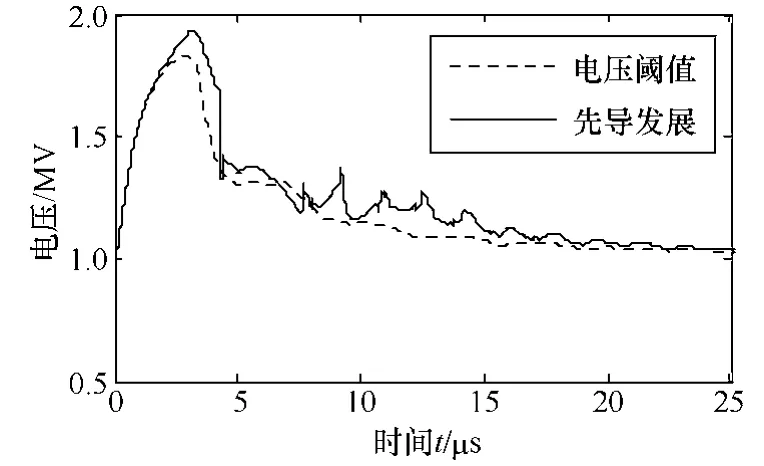
圖4 線路電壓仿真波形Fig.4 Simulation waveforms of voltage on transmission line

圖4中虛線表示沒有考慮先導發展（電壓閾值模型）的過電壓波形，實線表示考慮了先導發展仿真得到的線路過電壓波形。從圖4中可以看出實線與虛線相比，幅值更大、波頭更陡、電壓上升速度更快且波頭過后的時間內振蕩幅度更大，衰減慢。由此可見，采用先導法的線路過電壓波形的波頭更陡、振蕩持續時間更長，這是因為先導法考慮了雷電波在桿塔及輸電線路中的折、反射以及工頻電壓疊加的影響，也更符合實際情況[14]。因此，在研究輸電線路繞擊與反擊識別時，考慮先導的發展對線路雷擊過電壓的影響，將更加接近實際的物理過程。

本文分別以雷擊A相線路和桿塔頂部進行雷電繞擊與反擊仿真分析，相應的雷電過電壓波形分別如圖5和圖6所示。從圖5和圖6的仿真波形可以看出，考慮先導發展的雷電繞擊與反擊波形具有波頭陡、幅值大的特點，并且非閃絡相和閃絡相電壓都發生了高頻振蕩，實際過電壓錄波中很難從波形圖上直觀地判斷雷擊類型。為了能夠對輸電線路的繞擊與反擊進行快速且準確的識別，本文通過提取過電壓信號中的特征量進一步區分雷擊類型。

圖5 繞擊過電壓波形Fig.5 Shielding failure overvoltage

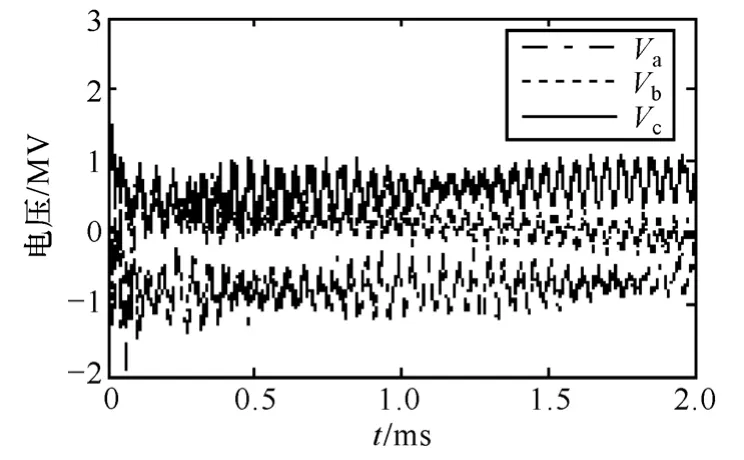
圖6 反擊過電壓波形Fig.6 Back striking overvoltage

4 輸電線路雷電過電壓識別判據

Hilbert-Huang（HHT）方法是黃鍔根據近代知名數學家 Hilbert的數學理論而提出的。HHT方法由兩部分組成：經驗模式分解（Empirical Mode Decomposition，EMD）和Hilbert變換。HHT方法具有良好的自適應性、快速性，非常適合對非平穩、非線性信號的分析[9,15]。

4.1 固有模式函數（Intrinsic Mode Function，IMF）

事實上，定義一個有意義的瞬時頻率要求函數關于局部零平均值對稱，并且過零點和極值點數量相同。因此提出了IMF的定義[16]：

（1）整個數據范圍內，極值點的數量與過零點的數量必須相等或相差一個。

（2）在任意點處，所有極大值點形成的包絡線和所有極小值點形成的包絡線的平均值為零。

4.2 經驗模式分解EMD

Hilbert變換不能對一個任意信號的頻率內容做完整分析，是由于多數信號不是IMF，在任意時刻，信號可能包含多個頻率模式，因此對一個信號的頻率特性進行完整分析時，需首先對該信號進行 EMD分解，得到IMF。EMD分解可形象地描述為“篩選”過程[16,17]，步驟如下：

（1）提取原始信號所有的極大值和極小值；然后用三次樣條函數曲線分別將所有的局部極大值點和極小值點進行連接，形成上、下包絡線。上、下包絡線之間應包含所有的原始信號數據。設上、下包絡線的均值函數為m1，計算原始信號x(t)與包絡均值函數m1的差值函數，記為h1。

（2）一般情況下，h1不是一個IMF，需要加以平滑化。用h1代替x(t)，重復步驟（1），直到得到一個滿足IMF條件的函數，記為c1，則c1為原始信號x(t)的第一個滿足固有模式函數條件的分量。

（3）將c1從原始信號x(t)中分離出來，得到殘余項，記為r1

然后將r1作為“原始信號”，重復步驟（1）和（2），得到第2個滿足固有模式函數的分量，并記為c2。反復循環步驟（1）～（3），則可以求出原始信號x(t)的第n個滿足固有模式函數的分量。則有

（4）rn變成單調函數時，原始信號x(t)分解結束，可以得到EMD的分解結果為

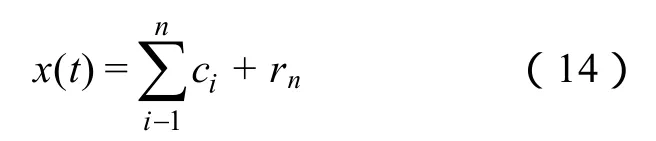
式中，rn稱為殘余函數。

信號經過 EMD分解后，得到一系列平穩的時域信號，這些時域信號的頻率依次降低，其中c1包含了原始信號中的最高頻率成分，c2次之，而rn是包含頻率最低的成分[18]。

4.3 希爾伯特譜分析

EMD分解結束后就得到了所有IMF，對第i階固有模式分量ci(t)進行Hilbert變換

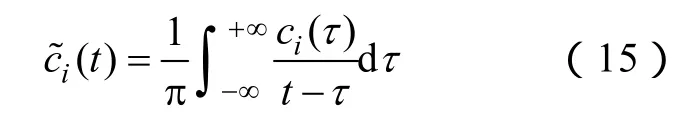
以ci(t)為實部、(t)為虛部構造解析信號

其中

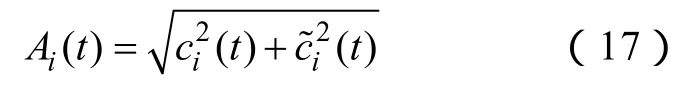
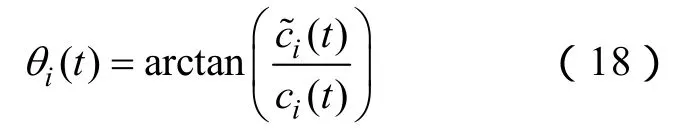
瞬時頻率為

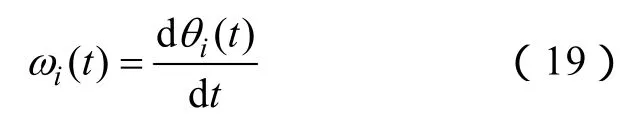
則原始信號x(t)可以表示為

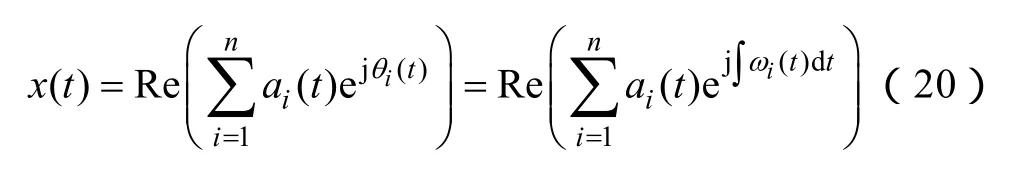
這里，沒有考慮余項rn，因為它只是單調函數或常量，Re表示取實部運算。由希爾伯特變換得出的振幅和頻率都是時間的函數，將這種振幅的頻率-時間分布定義為Hilbert幅值譜(,)Htω，簡稱Hilbert譜，記作

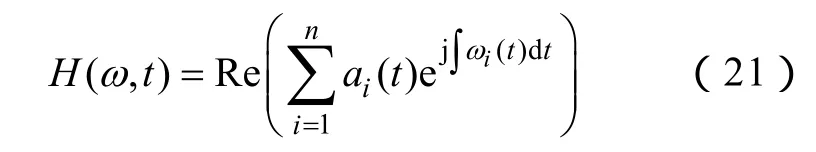
如用三維圖形表達幅值、頻率和時間之間的關系，可以把振幅用灰度的形式顯示在頻率-時間平面上。

4.4 過電壓信號的HHT分析及特征量提取

由 3.2節可知，雷電過電壓波形振蕩頻率高且包含大量的諧波，而且暫態過程中的特征頻率分量不固定，是一種典型的非平穩信號。因此，利用HHT對于非平穩信號分析非常適合的特點，將HHT運用在特高壓線路的雷擊過電壓信號分析和處理中是可行的。文章以雷擊線路A相為例，運用HHT方法對線路雷電繞擊與反擊過電壓信號進行特征量提取和繞、反擊識別。具體分析步驟如下，對應的流程如圖7所示。

圖7 繞擊與反擊識別系統流程圖Fig.7 Identification flowchart of shielding failure and backing striking

（1）利用ATP-EMTP軟件仿真分析，獲得繞擊與反擊產生的過電壓波形。

（2）對繞擊與反擊過電壓進行 EMD分解，得到若干階相應的IMF。繞擊與反擊過電壓信號對應的EMD分解結果分別如圖8和圖9所示。

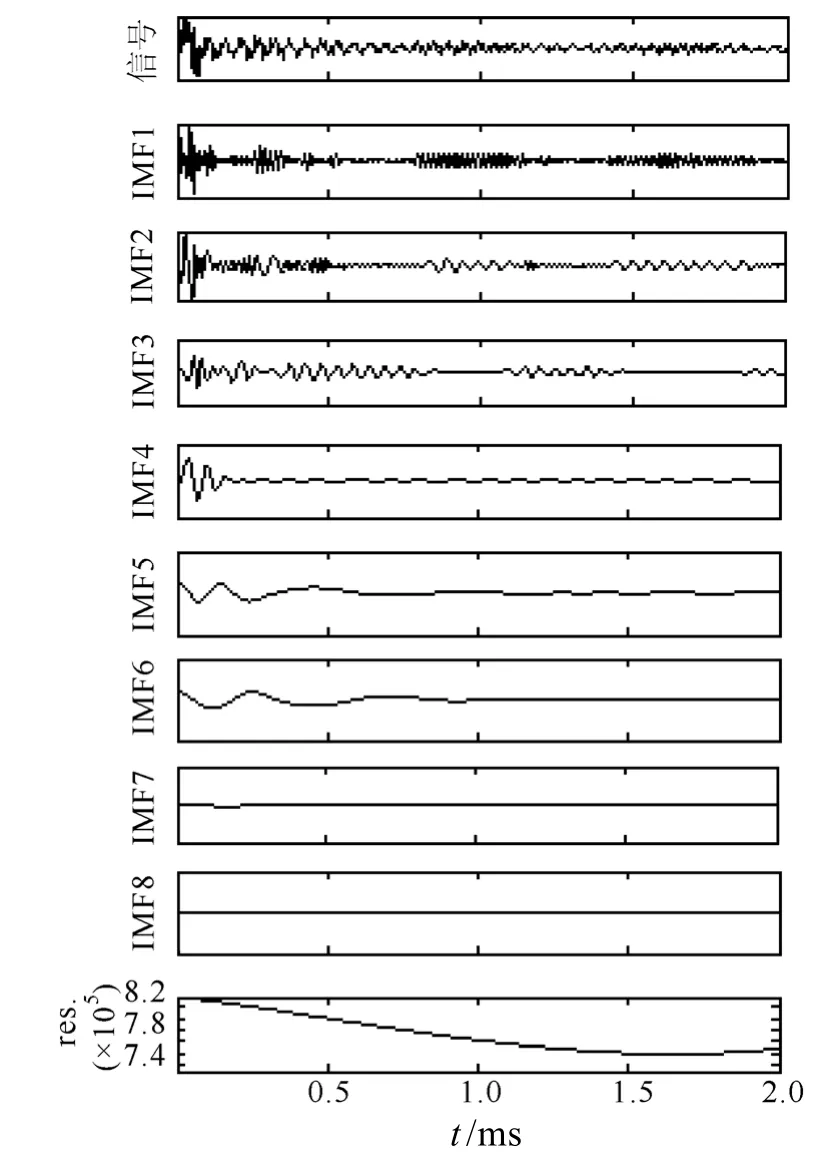
圖8 繞擊過電壓的EMD分解Fig.8 EMD decomposition of shielding failure overvoltage

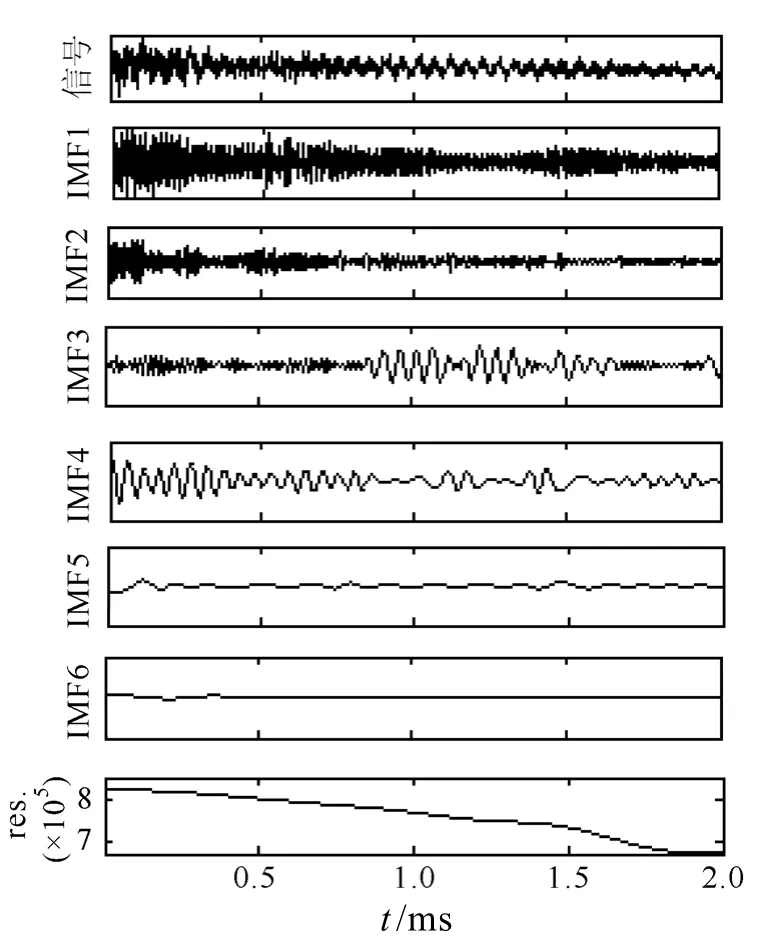
圖9 反擊過電壓的EMD分解Fig.9 EMD decomposition of back striking overvoltage

（3）EMD分解得到若干階 IMF后，對前四階IMF進行Hilbert變換，得到其瞬時幅值。

（4）計算各IMF瞬時幅值的方差貢獻率。方差貢獻率表示第i個元素的方差在全部方差中所占的百分比，能夠描述第i個元素綜合信息的能力大小；方差分量（Variance Component）貢獻率大，說明在這個事件中（100%）所占內容多，為主效應。

方差貢獻率為

（5）把計算所得任意IMF瞬時幅值的μi的值與閾值ρ比較，若μi≥ρ即為反擊，否則為繞擊。此處μi為對應的前四階IMF瞬時幅值的方差貢獻率，ρ為判據門限值，根據經驗設定。

EMD過程即是將原始信號按照不同尺度的波動或趨勢逐級分解成若干個IMF，因為繞、反擊過電壓信號中包含的故障信息不一樣，所以分解得到的IMF和其階數都不同。根據圖8和圖9可以看出，階數越靠前的IMF的頻率越高，振蕩越明顯且振蕩隨著時間逐漸減弱，這與圖5和圖6中的A相電壓隨時間變化的趨勢是一致的。頻率較高的前幾階IMF包含了原始信號中最顯著、最重要的信息，這是由IMF信號的本性所決定的，它們能比較全面地反映出原始信號的特征，因此本文選取前四階IMF來進行分析和特征量的提取。將前四階 IMF經過Hilbert變換后得到其對應的IMF瞬時幅值，分別如圖10和圖11所示。

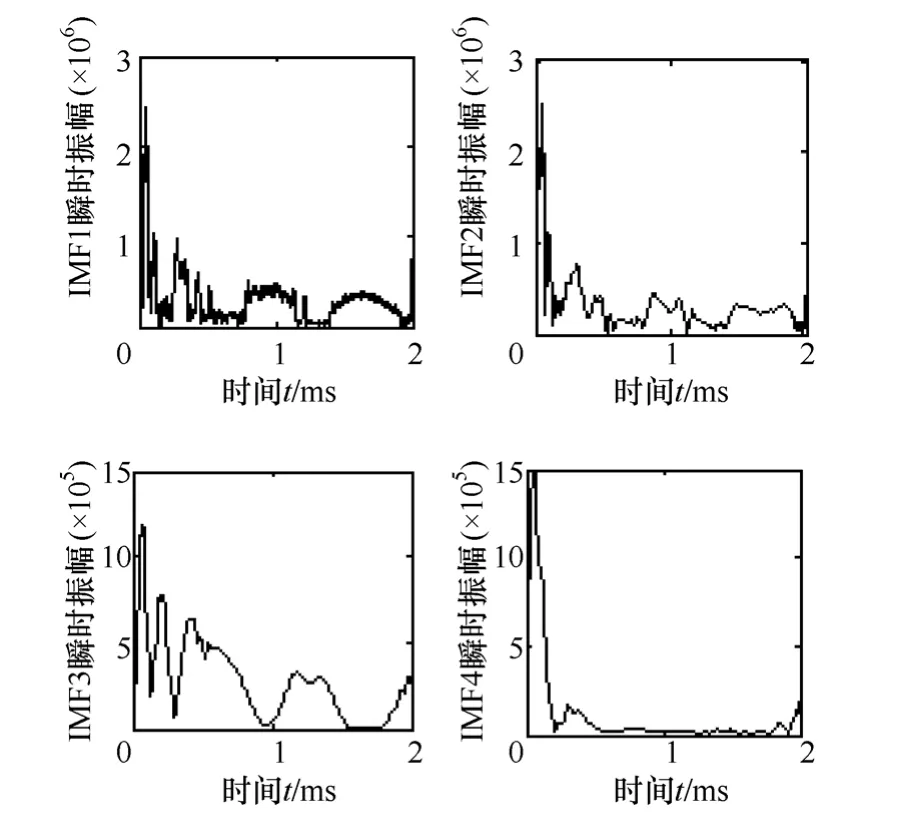
圖10 繞擊過電壓IMF的瞬時幅值Fig.10 Instantaneous amplitude of the shielding failure overvoltage’s IMF

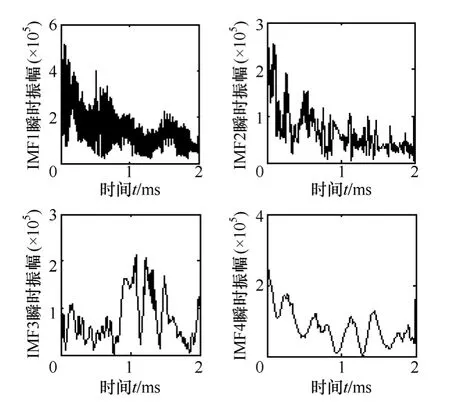
圖11 反擊過電壓IMF的瞬時幅值Fig.11 Instantaneous amplitude of the back striking overvoltage’s IMF

從圖10和圖11可以看出，當線路雷擊閃絡后幅值迅速增大且大幅振蕩，這與ATP-EMTP仿真結果是相符合的。該幅值譜較IMF比較而言，能夠更準確地反映原始信號的內部特性，可用來檢測突變信號，因此選取 Hilbert變換得到的前四階 IMF的瞬時幅值作為特征量，并以計算其方差貢獻率μi。方差貢獻率的差異不僅描述了該瞬時幅值譜對應的IMF表達信息的能力大小，而且也反映了原始信號的內部特征的區別。因此，選取μi作為識別的判據能夠對繞、反擊進行有效區分。

繞、反擊時的IMF瞬時幅值的方差貢獻率分別如圖12和圖13所示。從圖12和圖13中可知，繞擊時，前四階IMF瞬時幅值的方差貢獻率比較均衡且都在40%以下。而反擊時則IMF1分量占主要部分，μ1=49.582%，其他分量的方差貢獻率比較均衡且占的比重比較小。根據方差貢獻率整體分布的特點，將μi與設定的判據門限值ρ比較用來進行繞、反擊的識別。

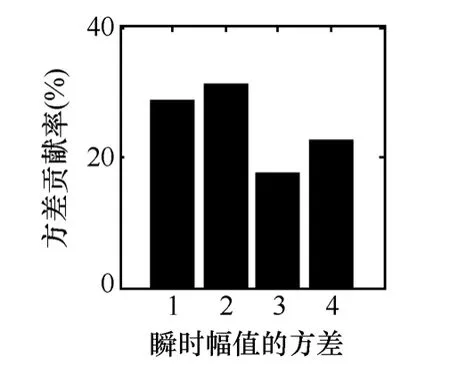
圖12 繞擊時IMF瞬時幅值方差貢獻率Fig.12 Variance contribution rate of the shielding failure instantaneous amplitude IMF component

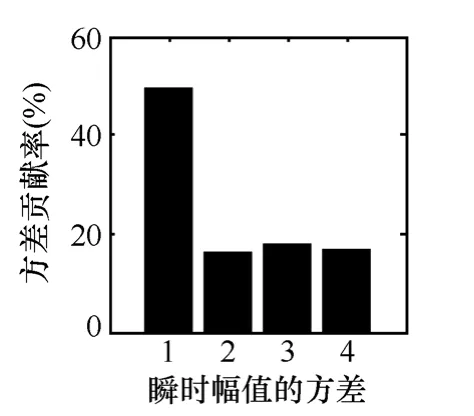
圖13 反擊時IMF瞬時幅值方差貢獻率Fig.13 Variance contribution rate of the back striking instantaneous amplitude IMF component

5 繞擊與反擊識別方法的驗證

在前文理論分析的基礎上，通過改變桿塔接地電阻的大小和雷電流幅值，對本文方法進行了驗證分析，分析結果見表1。根據表1可知，繞擊時任意方差貢獻率都小于40%，且比重相差不大。反擊時μ1＞40%且占主要部分，其他剩余分量所占比例均勻，與μ1相比相差較大，故本文將ρ設定為40%。由表1數據分析可知，不同參數條件下，繞擊（反擊）過電壓的各 IMF瞬時幅值的方差貢獻率分布趨勢基本相同，改變接地電阻和雷電流幅值對判據沒有影響，可對線路繞擊與反擊做出正確的識別。因此該方法能有效地實現雷電繞、反擊方式的識別。

表1 繞擊與反擊特征參數Tab.1 Characteristic parameters of shielding failure and back striking overvoltage

為了驗證本文設計的雷電繞擊與反擊識別新方法在實際電網運行中是否可行，根據某多雷地區一變電站實際運行數據，運用本文所提出的識別方法進行驗證分析（受篇幅限制，略去詳細的驗證過程）。原始信號在沒有進行去噪的情況下進行驗證，結果見表2，繞擊和反擊識別率分別達到88.2%和92.3%，能達到預期效果。

表2 近3年線路運行雷擊記錄及識別結果Tab.2 The lightning records of line running nearly three years and recognition results

6 結論

（1）在研究特高壓交流輸電線路發生雷電繞擊與反擊時，本文考慮了雷電先導發展對雷擊暫態過程的影響。研究結果表明，考慮先導發展的線路過電壓波形具有以下特征：①線路雷擊過電壓波的波頭幅值明顯比采用電壓閾值模型的高，而上升速度更快；②雷擊過電壓波的陡度更高且在線路上衰減更慢，振蕩持續時間更長。以上研究結論更加接近雷擊線路時激發的線路過電壓波形的實際情況。

（2）本文運用HHT方法提取了特高壓線路雷電繞、反擊過電壓信號中高頻暫態信息，實現了線路雷電繞擊、反擊的有效識別。首先對繞擊、反擊過電壓波形進行 EMD分解，將分解后信號的前四階IMF進行Hilbert變換，把計算得到的瞬時幅值作為特征量，然后計算特征量所對應的方差貢獻率，將方差貢獻率作為繞擊與反擊的識別判據，實現雷擊繞擊、反擊的識別。仿真結果和變電站實測數據的分析表明該方法能夠正確有效地實現輸電線路繞擊與反擊的識別，且不受線路接地電阻和雷電流幅值的影響，具有較高的識別正確率。

[1] 維列夏金,吳維韓. 俄羅斯超高壓和特高壓輸電線路防雷運行經驗分析[J]. 高電壓技術,1998,24( 2):76-79.

Weilie Xiajin,Wu Weihan. The analysis of lightning protection for EHV and UHV transmission line in Russia[J]. High Voltage Engineering,1998,24(2):76-79.

[2] 劉振亞. 特高壓直流輸電技術研究成果專輯[M].北京: 中國電力出版社,2006.

[3] 鄒貴彬,高厚磊,朱峰,等. 輸電線路雷擊與故障的積分識別方法[J]. 電力系統保護與控制,2012,40(9): 43-48.

Zou Guibin,Gao Houlei,Zhu Feng,et al. Integral identification method of lightning stroke and fault for transmission line[J]. Power System Protection and Control,2012,40(9): 43-48.

[4] 李瑞芳,吳廣寧,曹曉斌,等. 輸電線路雷電繞擊率的三維計算方法[J]. 電工技術學報,2009,24(10):134-138.

Li Ruifang,Wu Guangning,Cao Xiaobin,et al. Threedimensional calculation method on shielding failure rate of transmission lines[J]. Transactions of China Electrotechnical Society,2009,24(10): 134-138

[5] 曾嶸,耿屹楠,李雨,等. 高壓輸電線路先導發展繞擊分析模型研究[J]. 高電壓技術,2008,34(10):2041-2046.

Zeng Rong,Geng Yinan,Li Yu,et al. Lightning shielding failure model of transmission line based on leader progress model[J]. High Voltage Engineering,2008,34(10): 2041-2046.

[6] 肖萍,汪沨,黃福勇,等. 基于連續先導的線路絕緣閃絡判據的研究[J]. 電網技術,2012,36(11):271-276.

Xiao Ping,Wang Feng,Huang Fuyong,et al. Research on criterion for line insulation flashover based on development of continuous leader[J]. Power System Technology,2012,36(11): 271-276.

[7] Taniguchi S,Okabe S,Takahashi T,et al. Discharge characteristics of 5m long air gap under foggy conditions with lightning shielding of transmission line[J].IEEE Transactions on Dielectrics and Electrical Insulation,2008,15(4): 1031-1037.

[8] 陳仕龍,束洪春,謝靜,等. 特高壓直流輸電線路故障暫態信號高頻特性研究[J]. 電力系統保護與控制,2012,40(21): 84-89.

Chen Shilong,Shu Hongchun,Xie Jing,et al. High frequency characteristic analysis of fault transient signal at UHVDC transmission lines fault[J]. Power System Protection and Control,2012,40(21): 84-89.

[9] 齊沖. 高壓輸電線路雷電繞擊和反擊的識別[D]. 南寧: 廣西大學,2007.

[10] 翟進乾. 配電線路在線故障識別與診斷方法研究[D]. 重慶: 重慶大學,2012.

[11] 吳文輝,曹祥麟. 電力系統電磁暫態計算與 EMTP應用[M]. 北京: 中國水利水電出版社,2012.

[12] Yamada T,Mochiznki A. Experimental evaluation of a LTHV tower model for lightning surge analysis[J].IEEE Transactions on Power Delivery,1999,10(1):630-635.

[13] Yang Pengcheng,Chen Shuiming,He Jinliang,et al.Lightning impulse corona characteristic of 1 000kV UHV transmission lines and its influences on lightning overvoltage analysis results[J]. IEEE Transactions on Power Delivery,2013,28(4): 2518-2525.

[14] Taniguchi S,Okabe S,Asakawa A,et al. Flashover characteristics of long air gaps with negative switching impulses[J]. IEEE Transactions on Dielectrics and Electrical Insulation,2008,15(2): 399-406.

[15] 劉毅力,陶學軍,李佳,等. 基于 HHT的風力發電機組滾動軸承故障特征提取[J]. 電力系統保護與控制,2012,40(20): 79-82,88.

Liu Yili,Tao Xuejun,Li Jia,et al. Feature extraction of rolling bearing for wind generator based on HHT[J].Power System Protection and Control,2012,40(20):79-82,88.

[16] Gu F C,Chang H C,Chen F H,et al. Application of the Hilbert-Huang transform with fractal feature enhancement on partial discharge recognition of power cable joints[J]. Science,Measurement & Technology,2012,6(6): 440-448.

[17] Huang N E,Shen Z,Long S R. A new view of nonlinear water waves: The Hilbert spectrum[J]. Annual Review of Fluid Mechanics,1999,31: 417-457.

[18] 公茂法,夏文華,李國亮,等. 變壓器和應涌流和勵磁涌流識別新判據[J]. 電力系統保護與控制,2012,40(18): 139-143.

Gong Maofa,Xia Wenhua,Li Guoliang,et al. New judgment to identify sympathetic inrush and inrush current[J]. Power System Protection and Control,2012,40(18): 139-143.