三相光伏并網發電系統THD及DCI優化方法研究
張國月 秦夢珠 齊冬蓮 吳 越 張建良
(浙江大學電氣工程學院 杭州 310027)
0 引言
新能源對于緩解當今世界能源短缺問題起到了關鍵的作用。太陽能光伏并網發電因具有清潔、高效等優點,近年來得到了快速發展[1]。然而,光伏并網發電系統的大規模應用,也造成了很多嚴重的問題。
首先,光伏并網發電系統中大量使用的電力電子裝置增大了入網電流總諧波畸變(Total Harmonic Distortion,THD)[2],嚴重降低了電能質量。其次,為避免工頻隔離變壓器對系統的體積、成本和能量轉換效率的不利影響,無變壓器非隔離型光伏并網發電系統得到了較快發展。然而,變壓器的移除卻又造成了諸如直流電流注入(Direct Current Injection,DCI)等問題。DCI不僅會導致地下設備腐蝕及變壓器飽和,而且對電氣設備的正常運行造成不良影響[3]。因此,減小入網電流THD和DCI,已成為光伏發電系統安全高效并網必須解決的關鍵問題。
為減小入網電流 THD,在優化逆變器拓撲結構、改善硬件性能的同時,也需要對其控制算法進行改進。目前,應用較為廣泛的并網逆變器控制方法包括旋轉坐標系下的PI控制方法及其改進策略[4-6]和靜止坐標系下的比例?諧振控制方法[7-9]等。但是這些控制方法均不能兼顧系統的穩定性與動態性能,且波形優化效果有限。
現有的DCI抑制策略主要包括:交流耦合電容隔直法[10]、基于飽和電抗器的偏置電流補償法[11]、虛擬電容法[12]和低成本鋁制電解電容隔直法[13]等。然而,成本、損耗、使用壽命和穩定性等問題,使得上述方法難以在工程實際中應用。
本文在上述研究的基礎上,分別提出 THD及DCI的優化策略,同時在討論了二者關系的前提下,提出了綜合優化方法。提出靜止坐標系下基于多個VPI控制器并聯的MVPI電流內環控制策略,在保證系統穩定性的同時,實現5、7、11、13次諧波的補償;提出基于低通模擬濾波電路和預測算法的DCI抑制技術,通過增加直流偏置電流控制環,實現DCI的抑制;探討二者關系,提出THD及DCI的綜合優化方法。設計一臺額定容量為10kW的光伏并網逆變器實驗樣機,實驗結果證明了算法的有效性。
1 VPI及MVPI
1.1 VPI
三相三線制光伏并網逆變系統輸出電流中主要含有階次為k=6n±1(n為整數,且n≥1)的正序(k=6n+1)和負序(k=6n?1)諧波電流,可通過添加諧波補償器的方法加以抑制。假設在諧波旋轉坐標系下,k次諧波以±kω1(正序分量以kω1作順時針旋轉,負序分量以?kω1作順時針旋轉,基波角頻率為ω1=314rad/s)旋轉,被控對象在k次諧波旋轉坐標系下的數學模型為(同步旋轉坐標系下的數學模型變換中包含k次諧波時的數學模型)
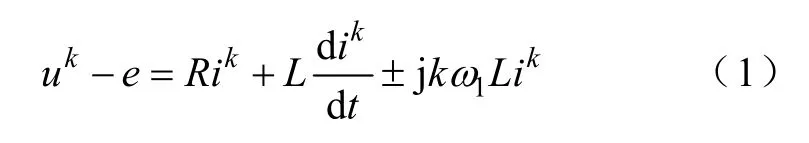
由式(1)可見,該系統存在復數極點R/L+jkω1,單純的含有實數零點的k次PI控制器無法實現復數極點的對消,因此,需要改進型k次 PI控制器[14]為
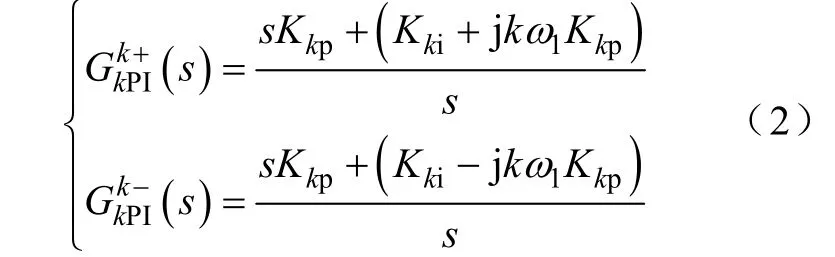
式(2)分別為諧波旋轉坐標系下的k次諧波正、負序分量控制器。通過旋轉變換,將改進型PI控制器變換到基波旋轉坐標系下(正序分量以+kω1作順時針旋轉,因此要用s?jkω1替代式(2)中的s;負序分量以?kω1作順時針旋轉,因此要用s+jkω1替代式(2)中中的s),即
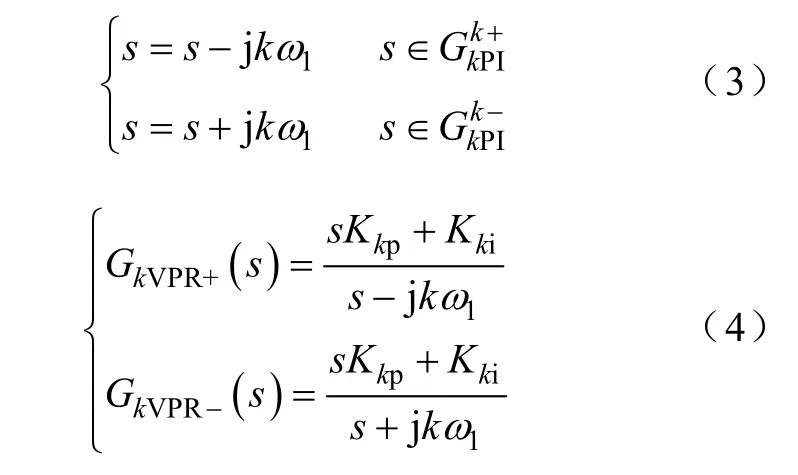
為在基波旋轉坐標系下同時實現諧波的正、負序分量的抑制,將GkVPR+、GkVPR?疊加,可得
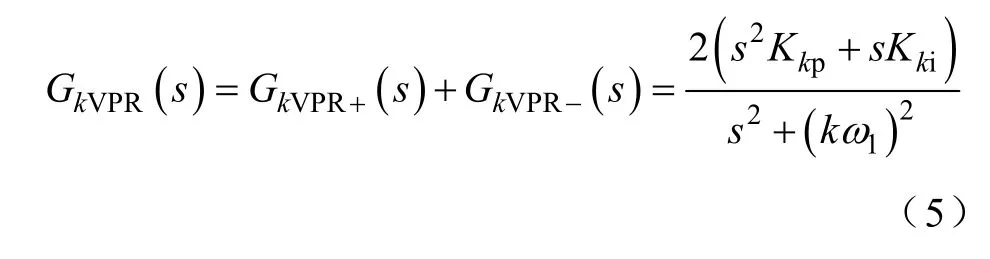
式(5)即為矢量比例積分控制器頻域表達式[15]。由該式可見,其表達形式與諧振控制器表達式類似,即
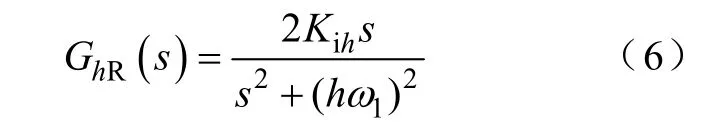
對式(5)進行等價變換,可得
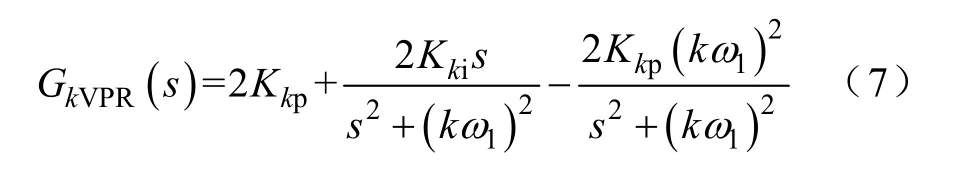
對上式進行Laplace反變換,可得
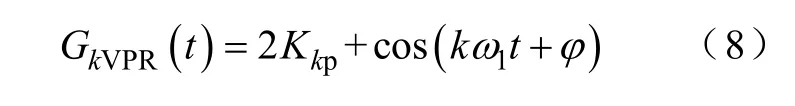
式中,φ=arctan(Kkpkω1/Kki)。可見,同諧振控制器類似,矢量比例積分控制器也是一種基于內模原理的控制器:通過將交流信號的動態模型cos(kω1t+φ)植入控制環,即可實現交流信號的跟蹤或抑制。比例環節2Kkp的加入,有利于系統動態性能的改善。
圖1所示為VPI控制器和諧振控制器的伯德圖,通過對比發現,在基波頻率處,諧振控制器存在180°的相位滯后,容易使系統失穩;VPI的相角最終穩定在0°相角處,表明其對低于諧振頻率的其他頻段輸入信號具有零相位滯后特性,不會對穩定性產生影響。
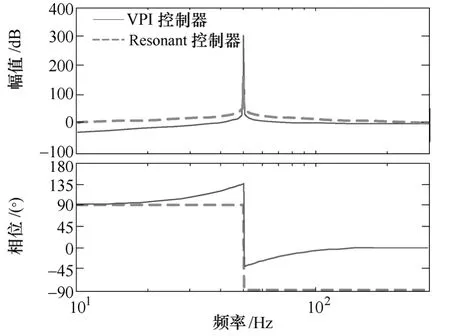
圖1 諧振控制器與矢量比例積分控制器的伯德圖Fig.1 Bode diagram of resonant controller and vector proportional integral controller
1.2 VPI參數設計
加入VPI后,電流內環閉環傳遞函數為
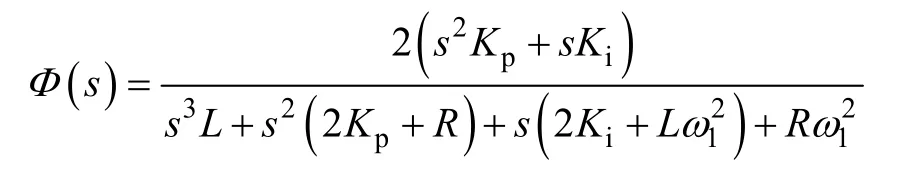
本文根據閉環系統根軌跡及開環系統伯德圖對VPI參數選取進行分析。
1.2.1Kp設計方法
穩態誤差是在交流信號跟蹤或抑制時必須考慮的問題,因此積分系數Ki一般取值較大。在進行Kp設計時,取Ki=500。Kp變化時,閉環系統根軌跡、VPI伯德圖和電流穩態誤差分別如圖2~圖4所示。
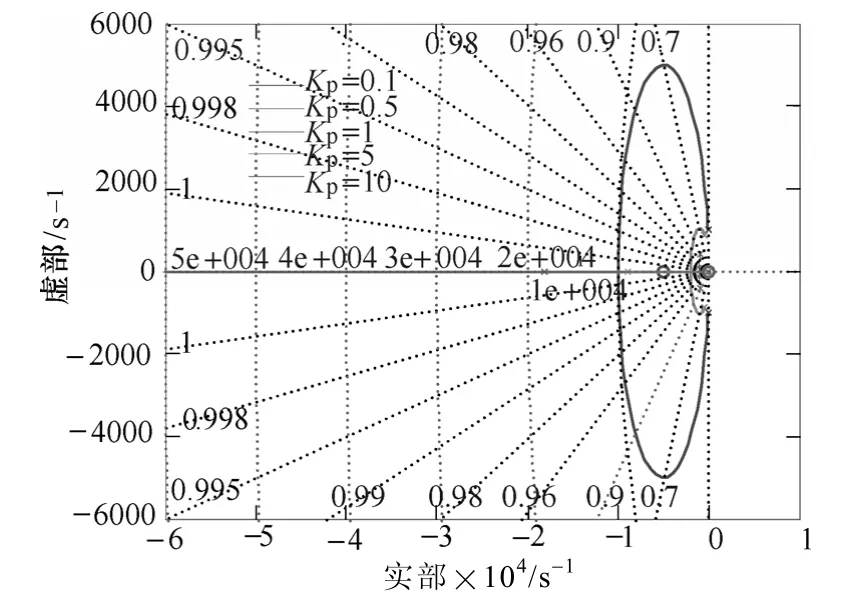
圖2 Kp變化時閉環系統根軌跡Fig.2 Root locus of closed-loop system asKpchanges
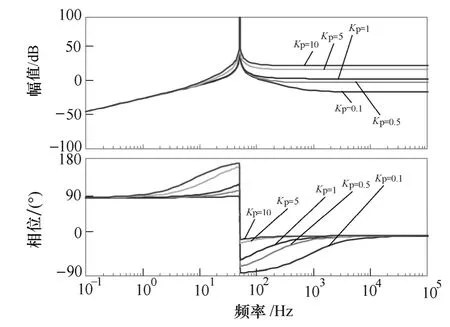
圖3 Kp變化時的VPI伯德圖Fig.3 Bode diagram of VPI asKpchanges
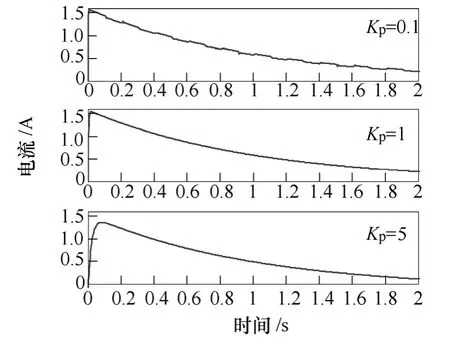
圖4 Kp變化時的電流穩態誤差Fig.4 Static state error of current asKpchanges
圖2中,隨著Kp的增大,閉環系統主導極點逐漸向虛軸靠近,當Kp≥1時,幅頻特性在大于特定諧振頻率時也將出現正向增益,會給其他頻率處的幅頻特性帶來影響,甚至會放大電流諧波,而當Kp=10時,閉環系統根軌跡已非常接近s域的右半平面,系統穩定性降低;圖3中,隨著Kp的增大,VPI的選擇性逐漸增強,即對基波或特定次諧波的跟蹤或抑制能力逐漸增強;圖4中,系統穩態誤差隨著Kp的增大而減小。
綜上,在進行Kp參數設計時,需綜合考慮其對系統穩定性、穩態誤差及動態響應能力的影響。在本文給定的系統參數范圍內,Kp取值范圍為Kkp≤1,k≥1。由以上分析也可以證明前文所得出的結論,即VPI中的Kp與PI控制器中的比例環節作用相同。
1.2.2Ki設計方法
同諧振控制中的積分增益類似,Ki的作用也是減小穩態誤差,提高系統跟蹤精度。
圖5中,Ki的變化對系統穩定性并無太大影響;圖6中,隨著Ki的增大,VPI的選擇性逐漸減弱,且在諧振頻率處,相位滯后隨之增大,而其恢復為0°相位的時間較長,因此,需要適當減小Ki的取值;圖 7中,穩態誤差隨著Ki的增大而減小,表明Ki對穩態性能具有改善作用。由以上分析可見,Ki的設計不宜過大,以避免其對VPI諧波補償性能的影響,本文取Ki=500。
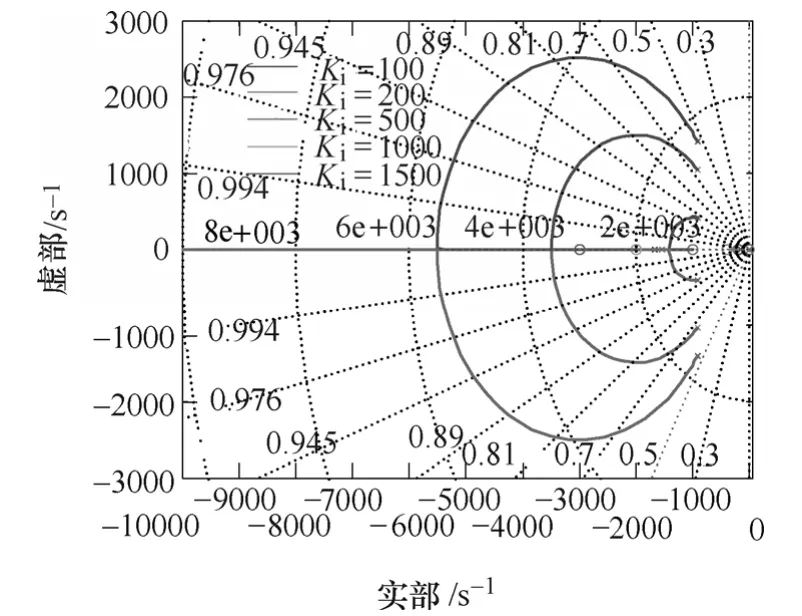
圖5 Ki變化時的閉環系統根軌跡Fig.5 Root locus of closed-loop system asKichanges
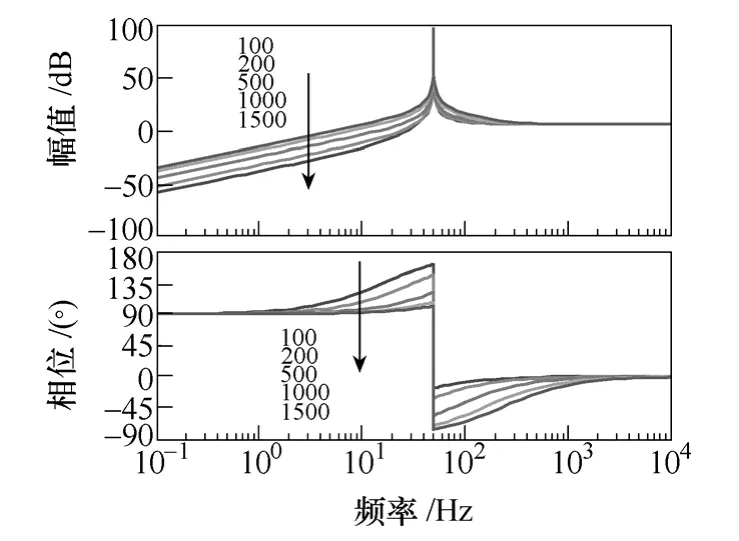
圖6 Ki變化時的VPI伯德圖Fig.6 Bode diagram of VPI asKichange
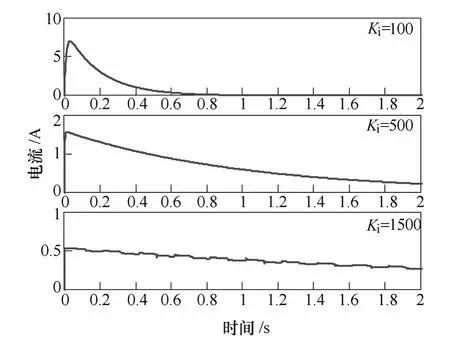
圖7 Ki變化時的電流穩態誤差Fig.7 Static state error of current asKichanges
1.3 MVPI
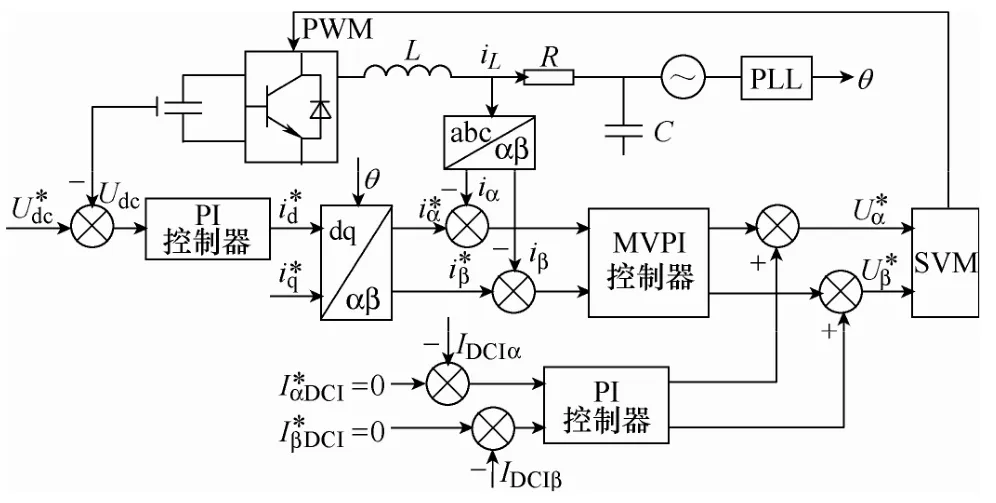
本文為消除旋轉坐標系下的控制路徑耦合,實現基波的有效跟蹤和諧波的完全補償,同時保證系統的穩定性和快速性,提出基波及5、7、11、13次諧波 VPI控制器并聯,構成 αβ兩相靜止坐標系下的多矢量比例積分控制器MVPI,如圖8所示。
2 DCI抑制策略
在電流檢測環節中,mA級的DCI很難被測量裝置準確地檢測,進而難以對其實現有效的抑制;測量裝置的加入,還有可能進一步加大直流分量的注入。本文設計一種非傳感器型直流檢測器件,并對檢測到的直流分量進行預測及控制。
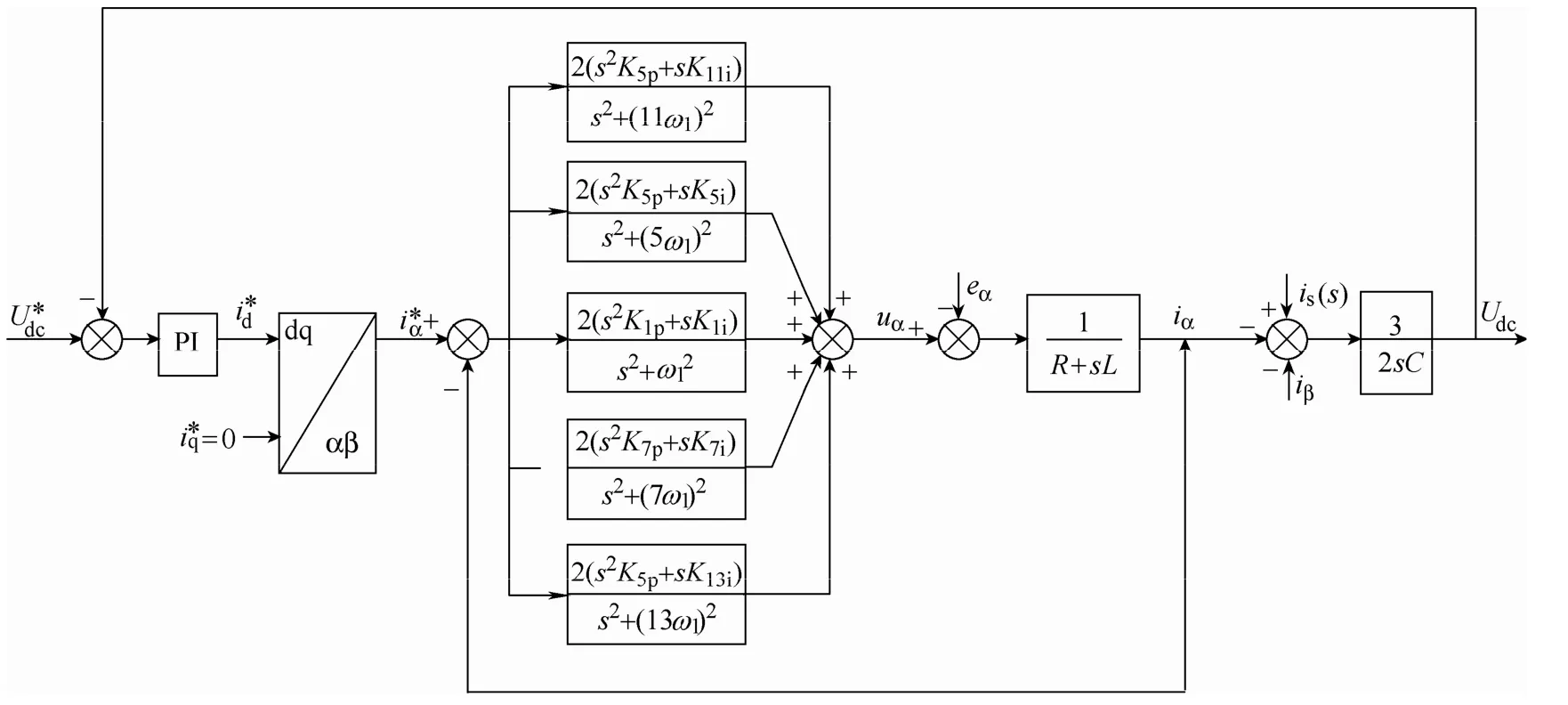
圖8 靜止坐標系下的逆變器控制框圖Fig.8 System control block diagram of inverter in stationary frame
2.1 直流偏置電流檢測及處理
直流偏置電流的控制,可通過添加DCI控制環實現。然而,控制環的加入必須以DCI的準確檢測為前提;電流傳感器的加入,又會在一定程度上加大DCI。本文設計一種高準確度、低成本的直流電流檢測裝置。
2.1.1直流偏置電流檢測裝置
本文所設計的DCI硬件電路主要分為采樣單元、直流分量提取單元和控制電路單元,如圖9所示。采樣單元將電流信號轉換成電壓信號。直流分量提取及處理單元中低通濾波電路實現正弦信號衰減,從而提取出微弱的直流信號,利用運放將小信號放大。
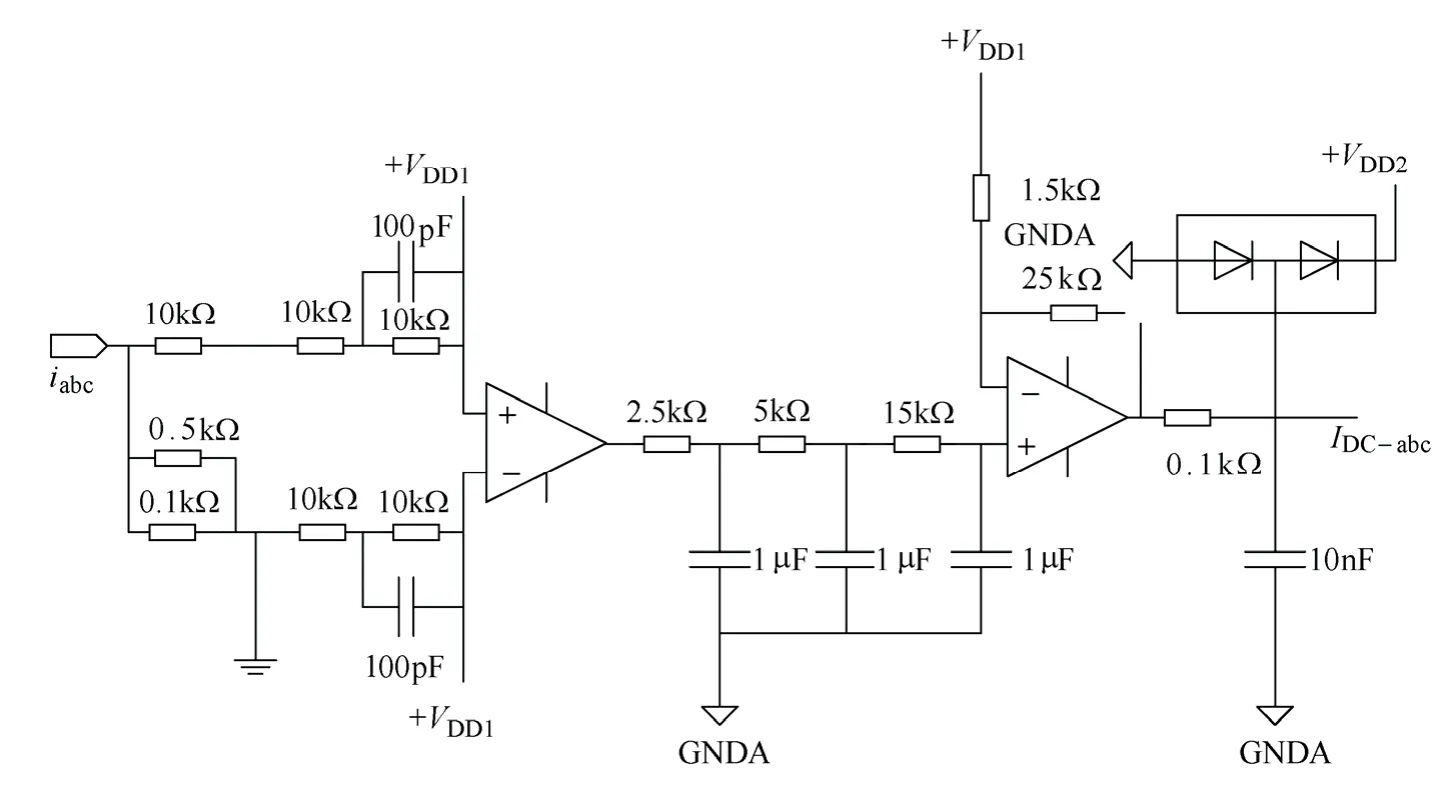
圖9 DCI采樣及濾波電路Fig.9 Sample and filter circuit of DCI
2.1.2直流偏置電流預測算法
硬件電路采樣的延時及直流偏置電流在 DSP內部的處理和計算造成的延時會使直流偏置電流的檢測產生誤差。本文通過對采樣值進行預測 1/2采樣周期的方法來減小該誤差[16],即
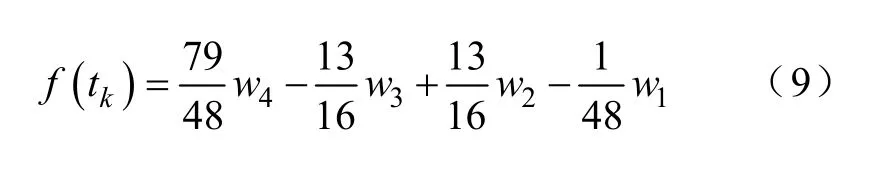
式中,f(tk)為預測值;wi(i=1,2,3,4)為采樣值。利用上式對直流電流分量檢測電路所得到的檢測值進行預測處理,可以提高檢測準確度,減小器件延時帶來的測量誤差。
2.2 直流偏置電流控制方法
利用預測算法得到DCI的校正值后,在電流控制內環增加直流偏置電流控制環,以抑制DCI。此時逆變器控制原理如圖10所示。
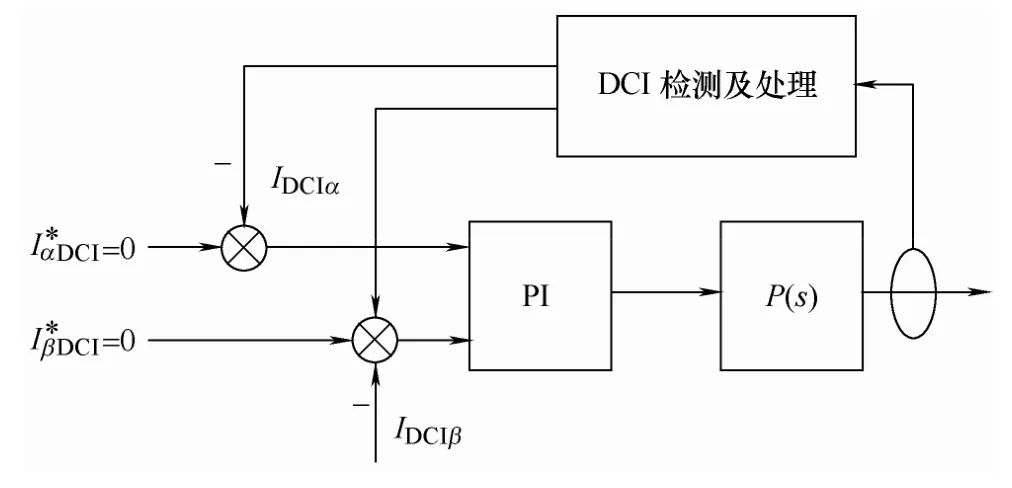
圖10 含直流偏置電流控制環的控制系統Fig.10 Control system with direct offset current control loop
3 THD與DCI綜合優化方法
3.1 THD與DCI
作為并網逆變器兩個最重要的性能指標,THD和DCI之間的相互關系影響到并網電能的質量,因此有必要對二者的關系進行分析。
首先探討一下THD對DCI的影響。假設并網電流中的直流分量包含因偏移誤差而產生的直流分量IDCOff和因電流諧波畸變而產生的直流分量IDCHar,即
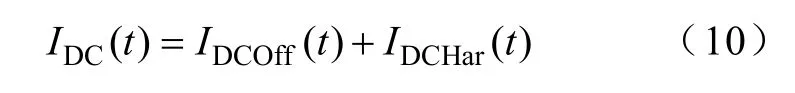
當輸出電流中不含有IDCOff(t)而含有基波及諧波分量時,其表達式為[17]
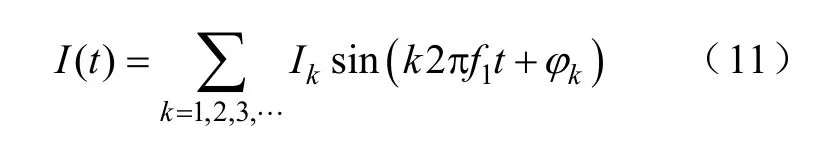
式中,k為諧波階次;φk為k次諧波相移。對該式進行時間間隔為周期T的積分運算,可得
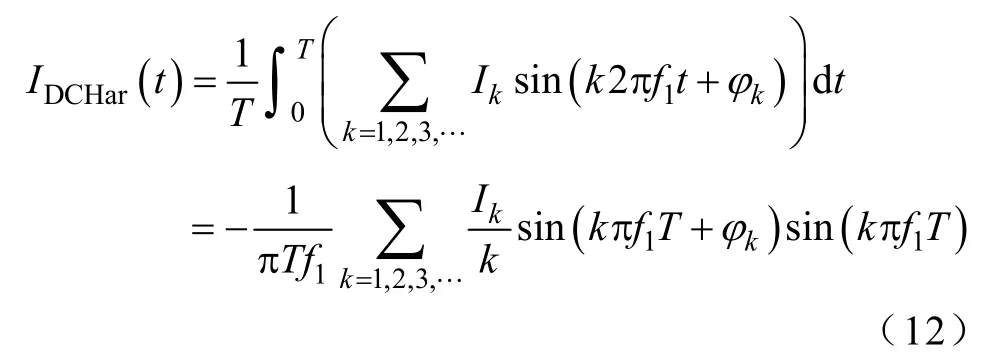
由上式可知,當T=1/f1時,IDCHar(t)=0,此時輸出電流不會因為諧波的問題而產生DCI。然而,實際應用中,輸出基波電流頻率f1的檢測需要依靠鎖相環實現[18],如圖11所示。
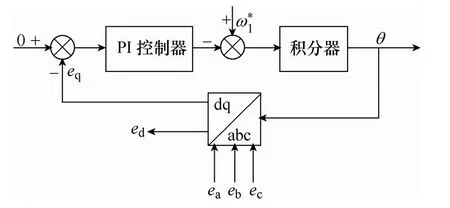
圖11 鎖相環原理Fig.11 The schematic diagram of the phase-locked loop
當入網電流存在較大波形畸變,且并網點阻抗較大時,會引起電網電壓波形畸變,使得eq中含有較大的諧波成分,進而導致頻率(或相位)的檢測出現較大偏差,假設該偏差為Δf,即此時基波頻率檢測值為f1′=f1+Δf,代入式(11),可得
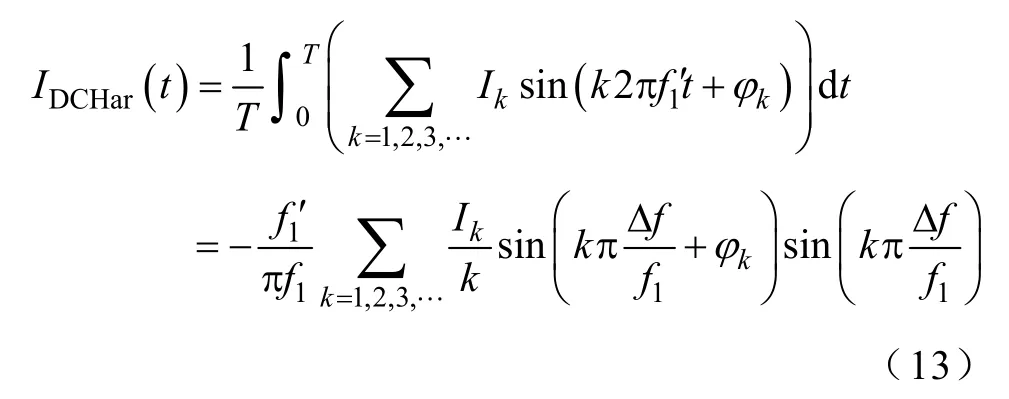
由式(13)可知,當Δf< 下面分析因偏移誤差而產生的直流分量IDCOff(t)對輸出電流THD的影響。電流諧波總畸變率為 式中,Ik(k=1,2,3,…)為入網電流有效值。當入網電流中含有IDCOff(t)時,會造成各次諧波均產生一定程度的幅值偏移,假設該偏移量為ΔIkDCOff(t),有 由上式可得 由上式可知,當入網電流中含有因偏移誤差而產生的直流分量時,其THD值會受到影響而變大。 綜上,THD與DCI之間存在著緊密的聯系,一方性能的改善必然會提高另一方的性能,反之亦然。 由上節分析可知,將THD、DCI優化控制方法同時加入系統中時,不僅可以實現各自性能的優化,而且還會產生相互影響,使得二者性能得到進一步改善。據此得到THD、DCI綜合優化控制框圖,如圖12所示。 圖12 含直流偏置電流控制環的控制系統Fig.12 Control system with direct offset current control loop 由于 MVPI實現對 50Hz基波分量的跟蹤及更高頻次諧波分量的抑制,而DCI抑制策略實現對直流分量(<3Hz)的抑制,頻帶寬度相差較大,因此二者在控制上并無直接關聯和影響。 本文設計了額定功率為10kW的三相光伏并網發電系統的開關電源,利用可編程序DC Source模擬光伏陣列,將逆變器輸出端直接并入電網。利用精確功率分析儀測量輸出電流中的THD及DCI。通過示波器檢測輸出電流、電壓波形并進行FFT分析。算法1:dq坐標系下PI控制策略;算法2:αβ坐標系下 THD優化控制策略;算法3:αβ坐標系下 DCI優化控制策略;算法4:αβ坐標系下綜合優化控制策略。光伏并網發電系統輸出電流波形如圖13所示。四種算法優化性能比較結果列于下表。 圖13 電流穩態波形及FFT分析Fig.13 Steady waveform and FFT analysis of output current 表 四種算法優化性能比較Tab.Performance comparison between four algorithms 圖14所示為利用差動探頭檢測到的輸出電流直流分量對應的用于DSP中A-D轉換的直流偏置電壓。 由圖13、圖14及下表可以看出,本文提出的算法4不僅可以有效改善系統電流波形質量,減小THD至最小,而且還可以很好地抑制輸出電流中的DCI,進一步提高光伏發電系統的電能質量。實驗充分證明了提出的方法可以實現THD及DCI的綜合優化。 圖14 三相輸出直流偏置電壓Fig.14 Three-phase DC offset voltage 本文主要進行了以下工作: (1)詳細推導了VPI的頻域表達式,并結合實際對象對其參數選取進行了分析,在此基礎上提出靜止坐標下的MVPI控制器,消除了傳統三相并網逆變器控制路徑上的耦合,提高了電能質量。 (2)設計了 DCI提取電路及其預測算法,并在電流內環增加了DCI控制環,減小了入網電流的直流含量。 (3)對 THD和 DCI的關系進行了詳細分析,得到了二者是正相關的關系。 (4)針對所提出的方法進行了實驗驗證,證明了所提方法(算法4)的有效性及優越性。 [1] 吳理博,趙爭鳴,劉建政,等.具有無功補償功能的單級式三相光伏并網系統[J].電工技術學報,2006,21(1):28-32. Wu Libo,Zhao Zhengming,Liu Jianzheng,et al.Implementation of a single-stage three-phase gridconnected photovoltaic system with reactive power compensation[J].Transactions of China Electrotechnical Society,2006,21(1):28-32. [2] 杭麗君,李賓,黃龍,等.一種可再生能源并網逆變器的多諧振 PR電流控制技術[J].中國電機工程學報,2012,32(12):51-58. Hang Lijun,Li Bin,Huang Long,et al.A multi-integral PR current controller for grid-connected inverters in renewable energy systems[J].Proceedings of the CSEE,2012,32(12):51-58. [3] Armstrong M,Atkinson D J,Johnson C M,et al.Auto-calibrating DC link current sensing technique for transformerless,grid connected,H-bridge inverter systems[J].IEEE Transaction on Power Electronics,2006,21(5):1385-1393. [4] 王飛,余世杰,蘇建徽,等.太陽能光伏并網發電系統的研究[J].電工技術學報,2005,20(5):72-91. Wang Fei,Song Shijie,Su Jianhui,et al.Research on photovoltaic grid-connected power system[J].Transactions of China Electrotechnical Society,2005,20(5):72-91. [5] Zhou K,Wang D.Digital repetitive learning controller for three-phase CVCF PWM inverter[J].IEEE Transaction on Industrial Electronics,2001,48(4):820-830. [6] 仇志凌,楊恩星,孔潔,等.基于 LCL濾波器的并聯有源電力濾波器電流閉環控制方法[J].中國電機工程學報,2009,29(18):15-20. Qiu Zhiling,Yang Enxing,Kong Jie,et al.Current loop control approach for LCL-based shunt active power filter[J].Proceedings of the CSEE,2009,29(18):15-20. [7] 張國月,曲軼龍,齊冬蓮,等.基于重復控制的三電平光伏逆變技術[J].浙江大學學報(工學版),2012,46(7):1339-1344. Zhang Guoyue,Qu Yilong,Li Ran,et al.Three-level photovoltaic inverter technology based on repetitive control[J].Journal of Zhejiang University(Engineering Science),2012,46(7):1339-1344. [8] Loh P C,Tang Y,Blaabjerg F,et al.Mixed-frame and stationary-frame repetitive control schemes for compensating typical load and grid harmonics[J].IEEE Transactions on Power Electronics,2011,4(2):218-226. [9] 陳煒,陳成,宋戰鋒,等.雙饋風力發電系統雙PWM 變換器比例諧振控制[J].中國電機工程學報,2009,29(15):1-7. Chen Wei,Chen Cheng,Song Zhanfeng,et al.Proportional-integral control for dual PWM converter in doubly fed wind generation system[J].Proceedings of the CSEE,2009,29(15):1-7. [10] Lee T L,Chen Z J.A transformerless interface converter for a distributed generation system[C].Power Electronics and Motion Control Conference,EPE-PEMC 2008,2008:1704-1709. [11] Buticchi G,Lorenzani E,Franceschini G.A DC offset current compensation strategy in transformerless gridconnected power converters[J].IEEE Transaction on Power Delivery,2011,26(4):2743-2751. [12] 王寶誠,郭小強,梅強,等.無變壓器非隔離型光伏并網逆變器直流注入控制技術[J].中國電機工程學報,2009,29(36):23-28. Wang Baocheng,Guo Xiaoqiang,Mei Qiang,et al.DC injection control for transformerless PV gridconnected inverters[J].Proceedings of the CSEE,2009,29(36):23-28. [13] Blewittl W M,Atkinsonl J J,Kelly J,et al.Approach to low-cost prevention of DC injection in transformerless grid connected inverters[J].IEEE Transaction on Power Electronics,2010,25(1):111-119. [14] Lascu C,Asiminoaei L,Boldea I,et al.Frequency response analysis of current controllers for selective harmonic compensation in active power filters[J].IEEE Transaction on Power Electronics,2011,26(6):904-914. [15] Lascu C,Asiminoaei L,Boldea I,et al.High performance current controller for selective harmonic compensation in active power filters[J].IEEE Transaction on Power Electronics,2007,22(5):1826-1835. [16] 趙為.太陽能光伏并網發電系統的研究[D].合肥:合肥工業大學,2003. [17] Wang B C,Guo X Q,Mei Q,et al.Real-time DC injection measurement technique for transformerless grid-connected PV inverter application[C].IEEE 2nd International Symposium on Power Electronics for Distributed Generation Systems,Rome,Italy,2011. [18] 龔錦霞,解大,張延遲.三相數字鎖相環的原理及性能[J].電工技術學報,2009,24(10):94-99. Gongn Jinxia,Xie Da,Zhang Yanchi.Principle and performance of the three-phase digital phase-locked loop[J].Transactions of China Electrotechnical Society,2009,24(10):94-99.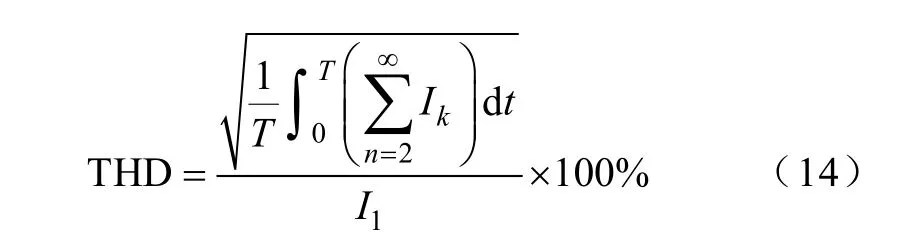
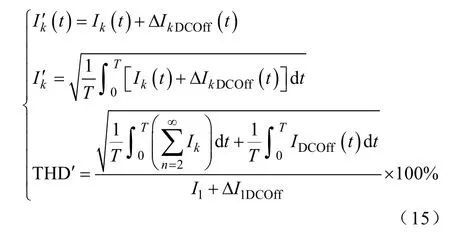
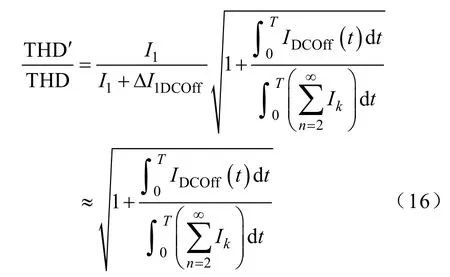
3.2 綜合優化方法
4 實驗驗證
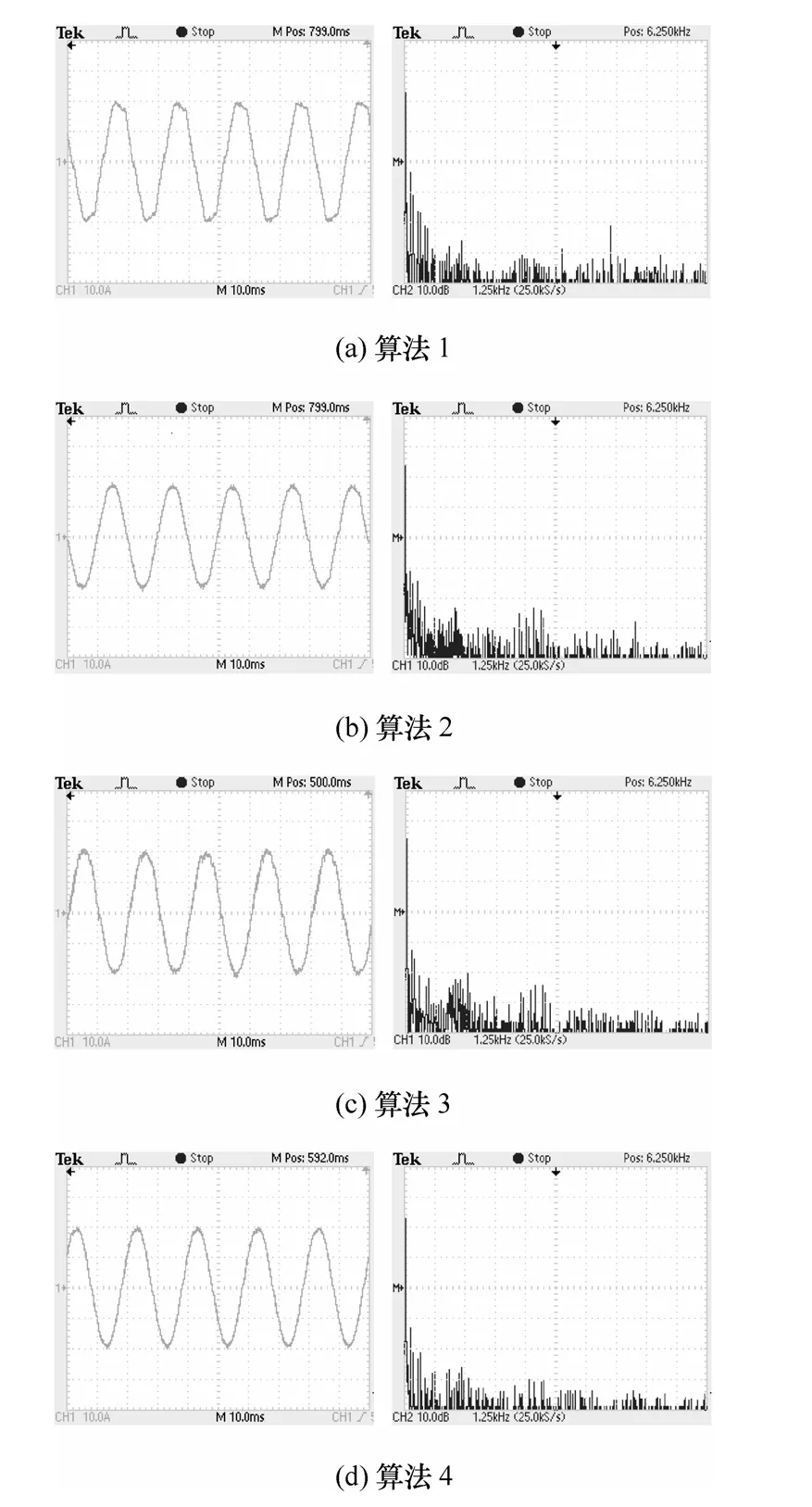
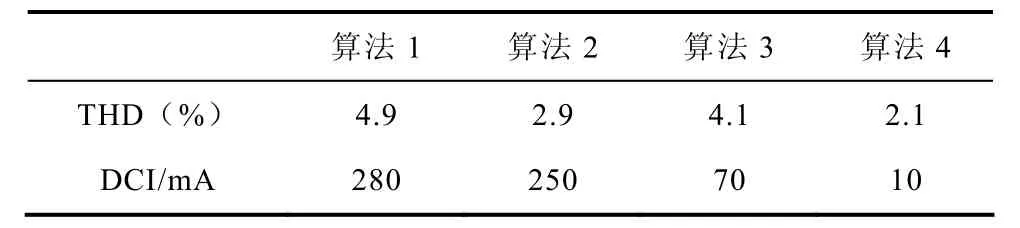
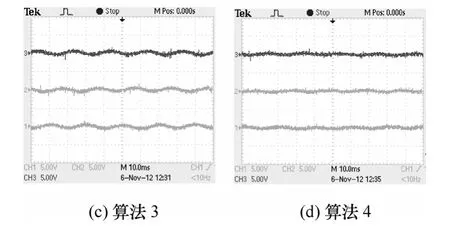
5 結論

