用于索網張拉結構找形的幾何非線性有限元法綜述

改造者：尤國強 劉 輝 胡景勤

用于索網張拉結構找形的幾何非線性有限元法綜述

改造者：尤國強 劉 輝 胡景勤

索網張拉結構在施加預張力之前是柔性體，只有對其施加一定的預張力后才能使其具有確定的形狀和剛度。索網張拉結構的找形計算可以得到索網張拉后的形態、張力分布和結構剛度等結構性能結果。本文介紹了索網張拉結構找形的相關概念，并根據已有文獻綜述了用于找形計算的幾何非線性有限元法的基本原理和推導過程。

索網張拉結構找形中的狀態定義

在對索網張拉結構進行找形計算時，根據索張力的施加過程，可對應將索網張拉結構的形態劃分為三個不同的狀態階段。

1.零狀態

零狀態時索網張拉結構中還未施加預張力，整個索網張拉結構可以看作僅是由一些具有給定幾何尺寸和位置的索段所組成的集合體。此時結構不存在預張力，也不承受外部荷載的作用。

2.自平衡狀態

自平衡狀態是指索網張拉結構在自身預張力的作用下達到的力平衡狀態。該狀態下，索網受到沿索網展開方向的張拉作用，由未受力時的柔性體，形成具有一定形狀和剛度的穩定結構。

3.外載荷工作狀態

外載荷工作狀態是指索網張拉結構在自平衡狀態的基礎上，受到外載荷（承重、風載等）作用所達到的力平衡狀態。該狀態可以反映出索網張拉結構的具體工作性能。

零狀態下的索網是由一些柔軟索段聯結而成的柔性體，沒有固定的形狀和剛度。當對零狀態下的索網沿展開方向進行張拉后，它將達到自平衡狀態，此時索網內的張力在仿真計算時被當作初始預張力來處理，而初始預張力的大小決定了索網的初始形狀和剛度。自平衡狀態在理論上可認為是在一定結構邊界約束條件和機構拓撲條件下，由索網張拉結構的幾何構型和施加的初始預張力相互作用所產生的結果。只有在索網張拉結構達到自平衡狀態從而具有一定的剛度后，它才能承受外部載荷，進入工作狀態。

因此，為了準確分析索網張拉結構的力學性能，就需要在給定索網索段長度、預張力大小和約束條件的情況下，先計算得到索網的自平衡狀態。而這個求解索網張拉結構初始平衡態的問題也就是通常所謂的索網張拉結構的找形問題。

工程上通常將索網張拉結構的找形問題分為以下三類。

1.指定拓撲形態時的索網找形問題

通常工程實際中需要索網張拉結構能夠形成指定的形狀，從而滿足諸如大跨度屋頂或天線反射面等結構的預定形狀要求。此時，需要在指定尺寸和位置的要求下，確定出索網張拉結構中索段的長度和索段內預張力值的大小。

2.指定預應力時的索網找形問題

有時為了滿足結構穩定性的要求，需要索網中的預應力具有指定的合理分布狀態。此時，為了滿足這一指定的預應力分布要求，則需要通過找形計算，確定出索網張拉結構的拓撲形態信息。

3.指定索網零狀態時的索網找形問題

當索網結構的索段長度、施加的預張力大小和拓撲形式都已經給定時，需要根據這些已知條件計算出索網張拉結構的形狀和力學性能，以便進一步進行后面的外載荷分析。

指定拓撲形態時的索網找形問題是工程中最常見的找形問題。

幾何非線性有限元法

從上世紀50年代末到60年代初，有限元法逐漸成為結構分析的主流方法。該方法是一種利用分片差值逼近的離散化方法。從工程和物理的角度來看，有限元法是把連續性問題轉化為離散問題并進行求解的方法；而從數學角度來看，有限元法是把偏微分方程轉化為代數方程并對其進行求解的方法。非線性有限元法正是在有限元法的基礎上發展起來的，它可以用于求解帶有非線性偏微分方程的復雜問題。

索網張拉結構的非線性特征主要體現在應變與位移的幾何非線性關系上，在對索網張拉結構進行非線性有限元分析時，首先需要根據索網張拉結構的拓撲形式將其離散成若干個獨立的索單元；然后以這些索單元為基礎建立各索單元的剛度矩陣；接下來再根據索單元在整體結構中的位置和相互連接關系，得到整體結構的總體剛度矩陣；最后由指定的邊界條件迭代求解相應的非線性有限元方程，從而得到自平衡態時的各索單元的節點位置和內力分布。

為了便于整體上的理解，下面將給出索網張拉結構幾何非線性有限元分析的普遍推導過程。

在對索網張拉結構進行非線性有限元分析時，需要先做出如下假設：

1.索段被假定為只能受拉、不能受壓的索桿單元；

2.索桿單元的材料特性滿足胡克定律。

對于離散后的結構，由虛功原理可寫出：

式中，δ｛d*｝T——虛位移；

δ｛ ε*｝T——對應于虛位移的虛應變；

｛σ｝——應力矩陣；

｛p｝——外載荷列陣。

由應變的增量形式，可得到應變和位移的關系為：

式中，［B］——應變矩陣。

上式即為增量形式的幾何方程，將此式代入式（1）可得：

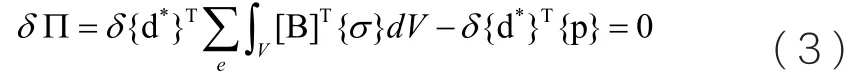
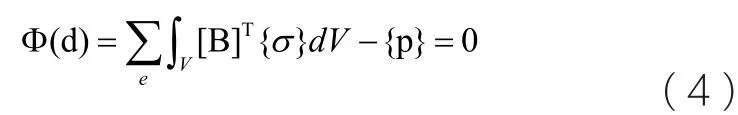
索網張拉結構中單元位移和單元應變之間的關系是非線性的，為了能夠明確表達出單元應變的物理意義，這里將應變矩陣寫為線性部分和非線性部分的組合形式：

［BNL］——索單元幾何非線性特性引起的非線性應變部分。

另外，對于索網張拉結構而言，其材料特性仍為線性狀態，即應力和應變之間仍呈線彈性關系，因此有：

式中，［D］——材料特性矩陣；

｛σ0｝——初應力矩陣。

由式（2）和式（7）可得：

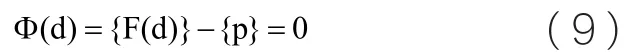
為了求切線剛度矩陣，將上式兩邊對｛d｝取微分，可得：

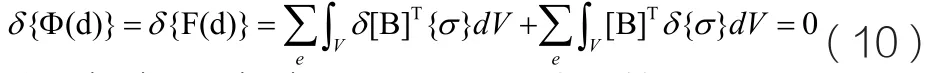
將式（6）和式（7）代入上面和式中的第一項可以得到：

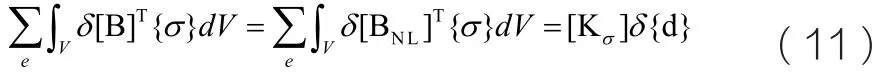
其中［Kσ］稱為初應力矩陣。

再將式（8）、式（5）代入式（10）中和式的第二項可得：

其中，［Ke］和［Kg］分別稱為彈性矩陣和初始位移矩陣，并有：

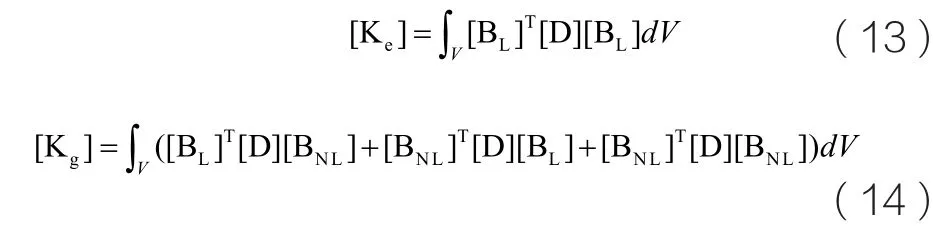
此時，平衡方程最終可寫為如下形式：

上面的［KT］稱為總切線剛度矩陣。

至此本文整理出了索網張拉結構的幾何非線性有限元方法的推導計算過程。這些推導為索網張拉結構的找形計算提供了理論依據，并可以作為理論基礎進一步進行索網張拉結構的外載荷平衡態分析計算和動力性能分析計算。

尤國強 劉 輝 胡景勤

西安翻譯學院

感謝陜西省教育廳專項項目（14JK2040）和院級科研項目（BK001）對本文的資助。

10.3969/j.issn.1001-8972.2015.16.040