高等數(shù)學(xué)教育價(jià)值的缺失與對(duì)策

張宇

（黑龍江交通職業(yè)技術(shù)學(xué)院 黑龍江齊齊哈爾 161000）

高等數(shù)學(xué)教育價(jià)值的缺失與對(duì)策

張宇

（黑龍江交通職業(yè)技術(shù)學(xué)院 黑龍江齊齊哈爾 161000）

為了能夠更好的發(fā)揮高等數(shù)學(xué)的教育價(jià)值與教學(xué)作用，教師應(yīng)該在今后的教育工作當(dāng)中更加的注重對(duì)專業(yè)知識(shí)內(nèi)涵的挖掘工作。本篇文章從自身角度出發(fā)，針對(duì)高等數(shù)學(xué)教育價(jià)值的缺失一題進(jìn)行了深入的研究，其中包括高等數(shù)學(xué)的教育價(jià)值、高數(shù)教材的思想內(nèi)涵以及高數(shù)教材當(dāng)中的人文內(nèi)涵等等，以期能夠?qū)Ω魑煌蕩?lái)一些具有參考性的意見(jiàn)。

高等數(shù)學(xué) 研究?jī)r(jià)值 對(duì)策分析

前言

高等數(shù)學(xué)教育對(duì)于理工科高校當(dāng)中的大學(xué)生來(lái)是非常重要的一門基礎(chǔ)類學(xué)科，然而，由于受到當(dāng)前我國(guó)應(yīng)試教育體系的影響，很多本專業(yè)當(dāng)中的教育者都比較的忽視對(duì)高等數(shù)學(xué)的價(jià)值與內(nèi)涵進(jìn)行深度的挖掘。筆者通過(guò)多方面的查找，發(fā)現(xiàn)具有著現(xiàn)實(shí)意義的研究成果數(shù)量較少，并且在水平上也還有著較大的進(jìn)步空間。基于此，筆者結(jié)合自身經(jīng)驗(yàn)對(duì)高等數(shù)學(xué)當(dāng)中的價(jià)值缺失現(xiàn)象進(jìn)行了分析，并嘗試總結(jié)了幾點(diǎn)可行性較高的應(yīng)對(duì)措施。

一、高等數(shù)學(xué)的教育價(jià)值

我國(guó)當(dāng)前的高等數(shù)學(xué)教育體系尚未發(fā)展的及其成熟，再加上此項(xiàng)學(xué)科的歷史研究文獻(xiàn)過(guò)于匱乏，所以也就無(wú)從談起有著教育價(jià)值的存在。那么，到底是何種原因造成高等數(shù)學(xué)的研究歷史如此缺少呢？筆者總結(jié)出了如下的三點(diǎn)原因：首先，目前我國(guó)高校當(dāng)中的課程普遍安排的非常滿，所以教師分本沒(méi)有時(shí)間和精力去研究課程的價(jià)值歷史；其次，我國(guó)大部分高校的高等數(shù)學(xué)課程教師一般都是身兼數(shù)職，專業(yè)的數(shù)學(xué)教師雖然本身的專業(yè)技能與教育水平都比較高，但是對(duì)高等數(shù)學(xué)的教育經(jīng)驗(yàn)卻不一定是非常的豐富，繼而更加無(wú)從談起開(kāi)展對(duì)高等數(shù)學(xué)教育課程的價(jià)值研究工作了；最后，就我國(guó)目前的教育現(xiàn)狀來(lái)看，高等數(shù)學(xué)的教學(xué)內(nèi)容同教學(xué)歷史價(jià)值的研究工作根本無(wú)法緊密的結(jié)合到一起。當(dāng)向?qū)W生講述有關(guān)于高等數(shù)學(xué)的價(jià)值內(nèi)容時(shí)，教師不應(yīng)該直接了當(dāng)?shù)南驅(qū)W生單純的灌輸一些純理論方面的內(nèi)容，而是應(yīng)該利用數(shù)學(xué)歷史當(dāng)中的價(jià)值閃光點(diǎn)而讓學(xué)生能夠與實(shí)際的課程內(nèi)容練習(xí)起來(lái)，繼而達(dá)到提高學(xué)習(xí)積極性的最終目的。

為了能夠改變當(dāng)前高等數(shù)學(xué)教育價(jià)值匱乏的現(xiàn)象，校方可以通過(guò)開(kāi)設(shè)數(shù)學(xué)史選修課程的方式。然而應(yīng)該注意的是，這種方式如果運(yùn)用不當(dāng)?shù)脑捑蜁?huì)讓數(shù)學(xué)史課程變得非常的枯燥的和乏味，讓學(xué)生對(duì)此門課程產(chǎn)生負(fù)面的情緒，繼而達(dá)不到預(yù)期的教學(xué)效果。更加合適的做法應(yīng)該是，將數(shù)學(xué)史的理論內(nèi)容與高等數(shù)學(xué)課程緊密的聯(lián)系到一起，同時(shí)教會(huì)學(xué)生如何去靈活的運(yùn)用數(shù)學(xué)史來(lái)提高自己的學(xué)習(xí)能力。這種做法不但能夠增強(qiáng)學(xué)生對(duì)于歷史的洞察能力，同時(shí)還可以提高他們對(duì)于數(shù)學(xué)概念的領(lǐng)悟能力。為此，教師需要明白，向?qū)W生傳授數(shù)學(xué)歷史的課程內(nèi)容其實(shí)就是在向他們講授如何學(xué)習(xí)高等數(shù)學(xué)的經(jīng)驗(yàn)與價(jià)值。舉例說(shuō)明：當(dāng)學(xué)生在學(xué)習(xí)調(diào)和級(jí)數(shù)之和的計(jì)算方法時(shí)，他們經(jīng)常會(huì)對(duì)其計(jì)算結(jié)果的無(wú)限性特點(diǎn)感到非常的感興趣，教師可以充分的利用這點(diǎn)來(lái)人讓學(xué)生自己的探索和尋找真相。或許在最開(kāi)始的時(shí)候?qū)W生會(huì)覺(jué)得這種探索的過(guò)程讓人覺(jué)得異常的困難與枯燥，通過(guò)教師一步步的引導(dǎo)，他們會(huì)漸漸的接近謎底，當(dāng)他們將自己的解題思路與方案提出后，教師就可以適時(shí)的向他們講授歷史當(dāng)中數(shù)學(xué)家們的解題方式。

著名數(shù)學(xué)家Johann Bernoulli的證明方法如下：首先一萊布尼茨收斂級(jí)數(shù)為計(jì)算的基礎(chǔ)理論，得出如下的計(jì)算結(jié)果：

另外

則得出

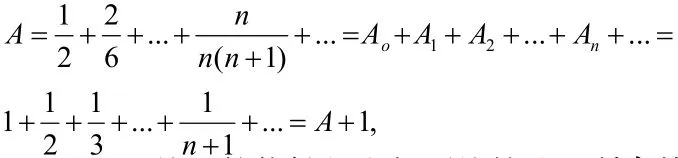
通過(guò)上面的計(jì)算能夠得出如下的結(jié)論，所有的限數(shù)都不會(huì)大于等于本身，繼而得出A是無(wú)限大的，即為和級(jí)數(shù)發(fā)散。

象上文當(dāng)中所提到的數(shù)學(xué)計(jì)算案例非常之多，教師應(yīng)該充分的利用這些數(shù)學(xué)史當(dāng)中的知識(shí)瑰寶來(lái)滲透到日常的教學(xué)當(dāng)中去。這種做法不但能夠在潛移默化中提高學(xué)生的數(shù)學(xué)計(jì)算能力，同時(shí)還能夠充分的將高等數(shù)學(xué)的教學(xué)價(jià)值顯現(xiàn)出來(lái)。

二、深度挖掘高數(shù)教材的思想內(nèi)涵

在開(kāi)展高數(shù)教學(xué)的過(guò)程當(dāng)中，有效的運(yùn)用數(shù)學(xué)思想的力量是及其有效的一種教學(xué)手段。為了能夠讓大學(xué)生們從根本意義上了解高等數(shù)學(xué)的重要性與顯性價(jià)值，教師應(yīng)該讓他們深刻的了解到數(shù)學(xué)思想在自主學(xué)習(xí)當(dāng)中的重要性。舉例說(shuō)明，教育者在向?qū)W生教授高數(shù)教材當(dāng)中的“定積分”課程時(shí)，應(yīng)先向他們闡述在此次的學(xué)習(xí)內(nèi)容當(dāng)中所能夠用到的各種思想方式，例如分割、逼近、換元和化歸等。其中比較主要的一個(gè)即為化歸，我們又可以稱之為不定積分。合理的運(yùn)用數(shù)學(xué)的思想方式不但能夠充分的調(diào)動(dòng)起學(xué)生的發(fā)散性思維模式，同時(shí)還可以讓他們充分的意識(shí)到深度挖掘教材內(nèi)容的重要性。此外，由于學(xué)生本身的閱讀能力和學(xué)習(xí)能力不是非常成熟，所以在進(jìn)行及其復(fù)雜的證明解題時(shí)無(wú)法正確的將最為主要的思想方式顯現(xiàn)出來(lái)。因此教師應(yīng)該充分的考慮這一問(wèn)題，同時(shí)引用些較為典型的例子來(lái)幫助學(xué)生去尋找正確的思想方式。

三、深度挖掘高數(shù)教材的人文內(nèi)涵

高數(shù)教材就如同是一個(gè)冰山美人一般讓人覺(jué)得難以接近，所以對(duì)于初經(jīng)世事的大學(xué)生們來(lái)說(shuō)根本不能夠很自如的去領(lǐng)悟到其中所蘊(yùn)含的人文氣息。基于此種情況，教師需要在原有的教學(xué)大綱中適當(dāng)?shù)募尤胍恍┤宋膬?nèi)容，其中包括數(shù)學(xué)理論的來(lái)源和發(fā)展歷史、數(shù)學(xué)家的解題思路簡(jiǎn)介以及具體的生產(chǎn)實(shí)踐方法等等。此外，在人文教學(xué)內(nèi)容當(dāng)中還應(yīng)該向?qū)W生展示出攻克數(shù)學(xué)難題所必須具備的堅(jiān)韌精神和執(zhí)著精神。舉例說(shuō)明，在向?qū)W生講述高數(shù)教材當(dāng)中的積分課題時(shí)，需要連帶告知學(xué)生積分理論是來(lái)源于牛頓和萊布尼茲所研究的流數(shù)理論和上三角形特征論。這兩位偉大的數(shù)學(xué)家都是歷經(jīng)了千辛萬(wàn)苦，犧牲了無(wú)數(shù)個(gè)本應(yīng)該同家人和朋友相聚的美好時(shí)光才探索出來(lái)的。隨后，當(dāng)積分論被提出后，有很多學(xué)術(shù)界的研究都在爭(zhēng)論這一數(shù)學(xué)理論的歸屬權(quán)，而牛頓與萊布尼茲卻不以為然，一直都用著高風(fēng)亮節(jié)的態(tài)度來(lái)面對(duì)來(lái)源于外界的爭(zhēng)論和質(zhì)疑。通過(guò)這些內(nèi)容的介紹，學(xué)生能夠更加珍惜當(dāng)前所學(xué)習(xí)到的這些寶貴的高數(shù)知識(shí)，深刻認(rèn)識(shí)到今天的學(xué)習(xí)是來(lái)源于歷代科學(xué)家與學(xué)術(shù)研究者們不辭辛苦的研究，繼而讓自己今后的高數(shù)學(xué)習(xí)生涯變得更加的充滿和諧和愉快。

［1］劉志高，張速，袁昌斌.再談復(fù)合函數(shù)求偏導(dǎo)數(shù)法則的證明［J］，秦州師范學(xué)院學(xué)報(bào)，2008，5（24）：20-21.

［2］沈文選.數(shù)學(xué)教育與教育教學(xué)［J］.數(shù)學(xué)通報(bào)，2005（9）：27-31.

［3］顧沛.南開(kāi)大學(xué)開(kāi)設(shè)“數(shù)學(xué)文化”課的做法［J］.2003，19（2）：23-25.

課題號(hào)：2013年度遼寧省高校統(tǒng)戰(zhàn)研究課題（高校黨外知識(shí)分子組織機(jī)構(gòu)建設(shè)研究與實(shí)踐+2013-GXTZA10）