借助幾何圖形解代數型問題舉例
覃禮權
(貴州省沿河縣客田中學 貴州沿河 565300)
借助幾何圖形解代數型問題舉例
覃禮權
(貴州省沿河縣客田中學 貴州沿河 565300)
數與形有著緊密的聯系,在一定條件下它們可以相互轉化,因此面對特殊的代數問題,可以將已知條件與幾何圖形建立聯系,把條件中的數量關系寓于特定的幾何圖形之中,就能迅速、準確地找到解題途徑。
幾何圖形 代數 數形結合 舉例
有些特殊的代數問題,已知條件中的數量關系蘊含著一定的幾何背景,具有明顯的幾何意義。如果我們將已知條件與幾何圖形建立聯系,把條件中的數量關系寓于特定的幾何圖形之中,常常能迅速、準確地找到解題途徑。下面舉例說明。[1]
例1、若正實數x、y、z、r滿足條件

求證:xy=zr。
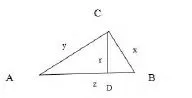
分析:如圖1,由條件⑴式可以構造直角三角形ABC,使AC=y,BC=x,AB=z,由條件⑵式聯想,作斜邊上的高CD,則CD=r,借助三角形面積并可以證明。
證明:在Rt△ABC中
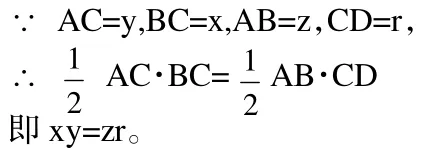
(圖1)
分析:構造如圖2所示的幾何圖形,其中AC⊥CD,BD⊥CD,AC=4, BD=3,PC=x,PD=y,則即a=AP+BP。作點B關于直線CD的對稱點F,連結AF,a的最小值為線段AF的長,作矩形CDFE,并可以求解。
在Rt△AEF中,AE=7,EF=6,由勾股定理得[2]

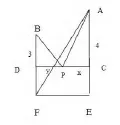
(圖2)
分析:如果用我們生活中的一些基本常識來解本題,是顯而易見的。例如,b克糖水中,內含a克糖,糖的質量分數為若再往糖水中加入m克糖,糖的質量分數就變為了糖水比開始也更甜一些。這表明
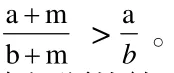
實際上,這個問題的結論我們還可以借助幾何圖形得出。
解:如圖3所示,由于0<a<b,所以S+S1>S+S2
即ab+bm>ab+am
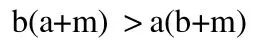
不等式兩邊同時除以正數b(b+m),得
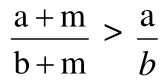

(圖3)
例4、試比較x2與 x|的大小。
分析:直接比較x2與 x|的大小不方便。如圖5,如果我們分別作出函數y=x2與函數y= x|的圖象,借助二圖像,很容易求解。[3]
解:如圖4所示,分別作出函數y=x2與函數y= x|的圖象。求出二圖象交點的橫坐標xA=-1,xB=1,xo=0
由圖象可知,
當x<-1或x>1時,
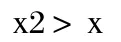
當-1<x<0時,
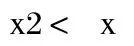
當x=±1或x=0時,
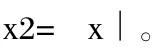
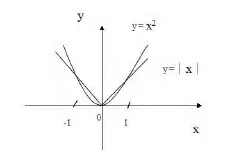
(圖4)
我們看到,以上例子都是利用了“數形結合”的思想。實際上,形與數是數學的兩大支柱數。數借形有直觀作用,而形借助于數可以找到內在規律。它們之間是沒有鴻溝的,也不是相割裂的,而是相輔相成、互相轉化的。學會用“數形結合”的思想分析和解決問題,就是要實現由數思形,以形助數,適時轉化、相互為用。
[1]李明,張銳.構造幾何圖形解決代數問題[J].數學教學研究,2012,31(2):67-67.
[2]董彪.淺議利用幾何圖形解決代數問題[J].阿壩師范高等專科學校學報,2003,(1):101-104.
[3]韋國友.巧構幾何圖形妙解代數問題 [J].中學生數學,2013,(20):17-17.

