正態分布的高精度數值計算

劉小會高海峰

（1.陜西科技大學鎬京學院 陜西西安712046；2.大唐移動通信設備有限公司 陜西西安710061）

正態分布的高精度數值計算

劉小會1高海峰2

（1.陜西科技大學鎬京學院 陜西西安712046；2.大唐移動通信設備有限公司 陜西西安710061）

近年來人們開始關注多維隨機變量的正態分布數值計算問題。由于多維正態分布積分函數較為復雜且計算量較大。因此研究多維正態分布積分數值計算方法具有強的理論和實際意義。本文首先利用參變量積分法，將多維分布降維計算，并給出了四維正態分布積分的詳細的計算公式，其次，在程序實現方面，考慮到相關系數較大時，會導致協方差矩陣接近奇異，如此以來會產生較大的計算誤差。因此對相關系數、積分變量進行有效的排序，在一定程度上減少精度損失。最后本章還創新性地比較了協方差矩陣不同分塊形式的數值計算公式，實驗結果表明計算精度有了較大提高。

正態分布 參變量積分法 精度

正文：

設n維隨機變量x1，x2，…xn服從正態分布并且協方差矩陣R非奇異，其聯合概率密度函數為［1］

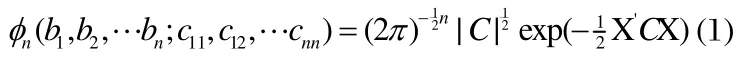
其聯合分布函數為

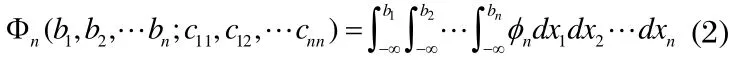
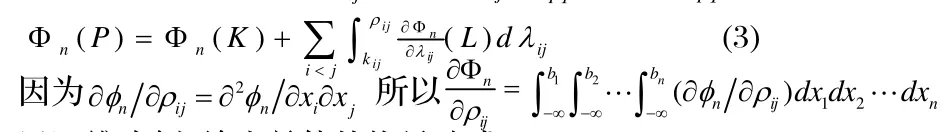
以四維為例，給出具體的推導公式。

四維聯合正態分布積分函數表達式為

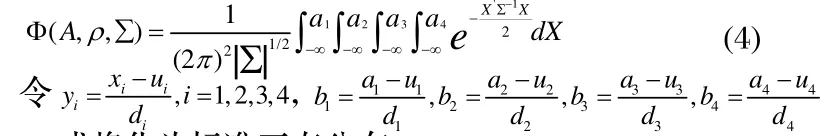
（4）式將化為標準正態分布

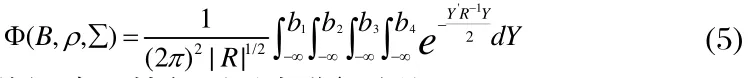
將矩陣R按如下形式進行分塊

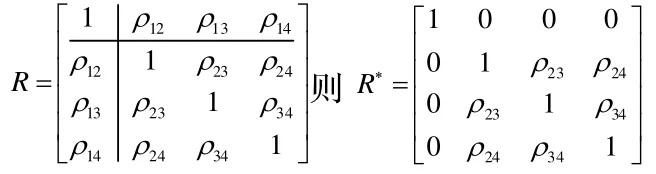
通過含參變量積分降階處理，（7）最終化為

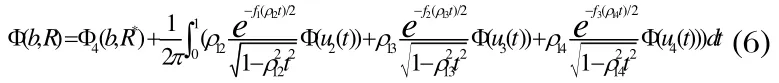
與此同時，也可將協方差矩陣按2-2分塊，經驗證，計算誤差沒有發生太大的變化。但對于五維正態分布，1-4分塊明顯沒有2-3分塊效果好，所以對高維矩陣分塊時，盡可能保證子塊之間維數相差較小。［3］

3.數值試驗

由于要求的精度較高，一般的曲線逼近效果不是很理想，所以本節給出數值試驗表。值得注意的是，當某些相關系數較大時，協方差矩陣在接近奇異時會產生較大的精度損失，因此程序實現是時，將協方差矩陣和積分變量進行適當的排序，在保證矩陣正定的情況下，盡可能避免矩陣接近奇異。［4］

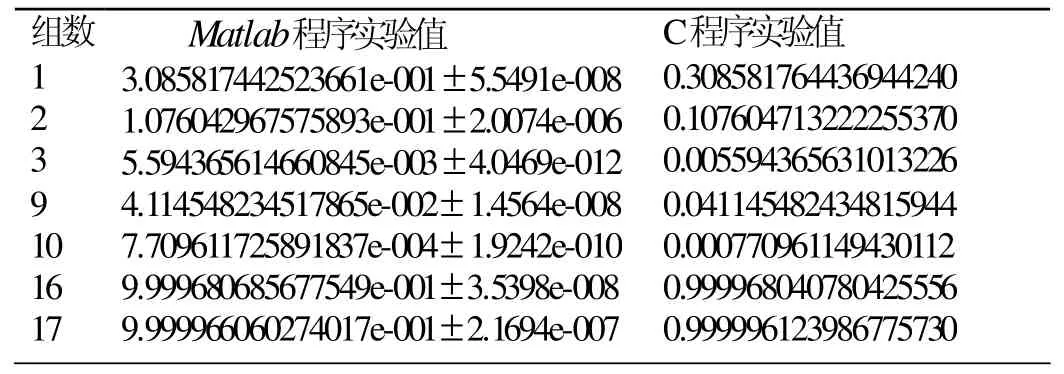
表1 四維正態分布新算法實驗值與Matlab值比較

實驗結果表明，本文的計算方法和適當的程序實現，最終能達到較高的要求。［5］

［1］Genz A.and Bretz F.Comparision of methods for the computation of multivariate t-probabilities.［J］Computing Science and Statistics.2002，11：950-971.

［2］Genz A.Numerical computation of rectangular bivariate and trivariate normal probalities［J］.Statistics and computing，2004，14：251 260.

［3］R.L.Plackett.A reduction formula for normal multivariate integrals［J］. Biometrika Trust.1954，413，351？360.

［4］Alan Genz.MCQMC methods for multivariate statistical distributions［J］.Springer Verlag.2008，21，164？191.

［5］劉小會.正態分布高精度算法［J］.長春理工大學學報.2011.34卷3期. 179-181

［6］Genz A.and Bretz F.Computation of multivariate normal and t-probabilitie［J］.Springer-Verlag.2009.